深度学习与计算机视觉教程(4) | 神经网络与反向传播（CV通关指南·完结）

深度学习与计算机视觉教程(4) | 神经网络与反向传播（CV通关指南·完结🎉）

本系列为 斯坦福CS231n 《深度学习与计算机视觉(Deep Learning for Computer Vision)》的全套学习笔记，对应的课程视频可以在 这里 查看。更多资料获取方式见文末。

---

引言

在上一篇 深度学习与CV教程(3) | 损失函数与最优化 内容中，我们给大家介绍了线性模型的损失函数构建与梯度下降等优化算法，【本篇内容】ShowMeAI给大家切入到神经网络，讲解神经网络计算图与反向传播以及神经网络结构等相关知识。

本篇重点

• 神经网络计算图
• 反向传播
• 神经网络结构

1.反向传播算法

神经网络的训练，应用到的梯度下降等方法，需要计算损失函数的梯度，而其中最核心的知识之一是反向传播，它是利用数学中链式法则递归求解复杂函数梯度的方法。而像tensorflow、pytorch等主流AI工具库最核心的智能之处也是能够自动微分，在本节内容中ShowMeAI就结合cs231n的第4讲内容展开讲解一下神经网络的计算图和反向传播。

关于神经网络反向传播的解释也可以参考ShowMeAI的 深度学习教程 | 吴恩达专项课程 · 全套笔记解读 中的文章 神经网络基础、浅层神经网络、深层神经网络 里对于不同深度的网络前向计算和反向传播的讲解

1.1 标量形式反向传播

1) 引例

我们来看一个简单的例子，函数为 f(x,y,z)=(x+y)zf(x,y,z) = (x + y) zf(x,y,z)=(x+y)z。初值 x=−2x = -2x=−2，y=5y = 5y=5，z=−4z = -4z=−4。这是一个可以直接微分的表达式，但是我们使用一种有助于直观理解反向传播的方法来辅助理解。

下图是整个计算的线路图，绿字部分是函数值，红字是梯度。（梯度是一个向量，但通常将对 xxx 的偏导数称为 xxx 上的梯度。）

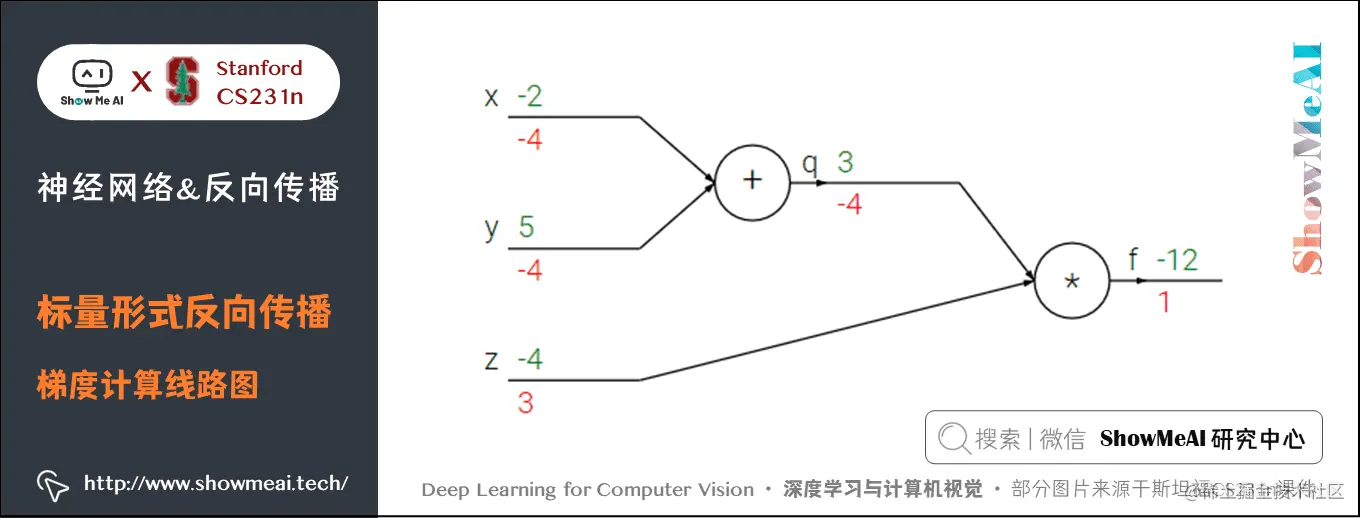
上述公式可以分为2部分， q=x+yq = x + yq=x+y 和 f=qzf = q zf=qz。它们都很简单可以直接写出梯度表达式：

• fff 是 qqq 和 zzz 的乘积， 所以 ∂f∂q=z=−4\frac{\partial f}{\partial q} = z=-4∂q∂f=z=−4，∂f∂z=q=3\frac{\partial f}{\partial z} = q=3∂z∂f=q=3
• qqq 是 xxx 和 yyy 相加，所以 ∂q∂x=1\frac{\partial q}{\partial x} = 1∂x∂q=1，∂q∂y=1\frac{\partial q}{\partial y} = 1∂y∂q=1

我们对 qqq 上的梯度不关心（ ∂f∂q\frac{\partial f}{\partial q}∂q∂f 没有用处）。我们关心 fff 对于 x,y,zx,y,zx,y,z 的梯度。链式法则告诉我们可以用「乘法」将这些梯度表达式链接起来，比如

∂f∂x=∂f∂q∂q∂x=−4\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial x} =-4∂x∂f=∂q∂f∂x∂q=−4

• 同理， ∂f∂y=−4\frac{\partial f}{\partial y} =-4∂y∂f=−4，还有一点是 ∂f∂f=1\frac{\partial f}{\partial f}=1∂f∂f=1

前向传播从输入计算到输出（绿色），反向传播从尾部开始，根据链式法则递归地向前计算梯度（显示为红色），一直到网络的输入端。可以认为，梯度是从计算链路中回流。

上述计算的参考 python 实现代码如下：

python复制代码# 设置输入值
x = -2; y = 5; z = -4

# 进行前向传播
q = x + y # q 是 3
f = q * z # f 是 -12

# 进行反向传播:
# 首先回传到 f = q * z
dfdz = q # df/dz = q, 所以关于z的梯度是3
dfdq = z # df/dq = z, 所以关于q的梯度是-4
# 现在回传到q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. 这里的乘法是因为链式法则。所以df/dx是-4
dfdy = 1.0 * dfdq # dq/dy = 1.所以df/dy是-4

'''一般可以省略df'''

2) 直观理解反向传播

反向传播是一个优美的局部过程。

以下图为例，在整个计算线路图中，会给每个门单元（也就是 fff 结点）一些输入值 xxx , yyy 并立即计算这个门单元的输出值 zzz ，和当前节点输出值关于输入值的局部梯度（local gradient） ∂z∂x\frac{\partial z}{\partial x}∂x∂z 和 ∂z∂y\frac{\partial z}{\partial y}∂y∂z 。

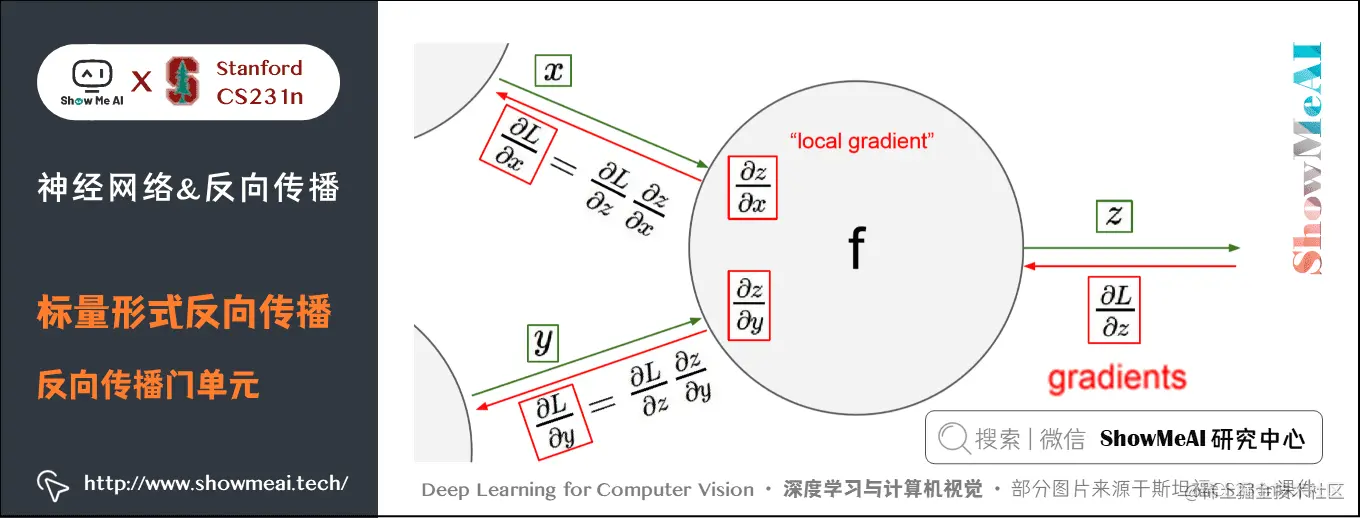
门单元的这两个计算在前向传播中是完全独立的，它无需知道计算线路中的其他单元的计算细节。但在反向传播的过程中，门单元将获得整个网络的最终输出值在自己的输出值上的梯度 ∂L∂z\frac{\partial L}{\partial z}∂z∂L 。

根据链式法则，整个网络的输出对该门单元的每个输入值的梯度，要用回传梯度乘以它的输出对输入的局部梯度，得到 ∂L∂x\frac{\partial L}{\partial x}∂x∂L 和 ∂L∂y\frac{\partial L}{\partial y}∂y∂L 。这两个值又可以作为前面门单元的回传梯度。

因此，反向传播可以看做是门单元之间在通过梯度信号相互通信，只要让它们的输入沿着梯度方向变化，无论它们自己的输出值在何种程度上升或降低，都是为了让整个网络的输出值更高。

比如引例中 x,yx,yx,y 梯度都是 −4-4−4，所以让 x,yx,yx,y 减小后，qqq 的值虽然也会减小，但最终的输出值 fff 会增大（当然损失函数要的是最小）。

3) 加法门、乘法门和max门

引例中用到了两种门单元：加法和乘法。

• 加法求偏导： f(x,y)=x+y→∂f∂x=1∂f∂y=1f(x,y) = x + y \rightarrow \frac{\partial f}{\partial x} = 1 \frac{\partial f}{\partial y} = 1f(x,y)=x+y→∂x∂f=1∂y∂f=1
• 乘法求偏导： f(x,y)=xy→∂f∂x=y∂f∂y=xf(x,y) = x y \rightarrow \frac{\partial f}{\partial x} = y \frac{\partial f}{\partial y} = xf(x,y)=xy→∂x∂f=y∂y∂f=x

除此之外，常用的操作还包括取最大值：

f(x,y)=max⁡(x,y)→∂f∂x=1(x≥y)∂f∂y1(y≥x)\begin{aligned} f(x,y) &= \max(x, y) \ \rightarrow \frac{\partial f}{\partial x} &= \mathbb{1}(x \ge y)\ \frac{\partial f}{\partial y} &\mathbb{1}(y \ge x) \end{aligned}f(x,y)→∂x∂f∂y∂f=max(x,y)=1(x≥y)1(y≥x)

上式含义为：若该变量比另一个变量大，那么梯度是 111，反之为 000。

• 加法门单元是梯度分配器，输入的梯度都等于输出的梯度，这一行为与输入值在前向传播时的值无关；
• 乘法门单元是梯度转换器，输入的梯度等于输出梯度乘以另一个输入的值，或者乘以倍数 aaa（axaxax 的形式乘法门单元）；max 门单元是梯度路由器，输入值大的梯度等于输出梯度，小的为 000。

乘法门单元的局部梯度就是输入值，但是是相互交换之后的，然后根据链式法则乘以输出值的梯度。基于此，如果乘法门单元的其中一个输入非常小，而另一个输入非常大，那么乘法门会把大的梯度分配给小的输入，把小的梯度分配给大的输入。

以我们之前讲到的线性分类器为例，权重和输入进行点积 wTxiw^Tx_iwTxi ，这说明输入数据的大小对于权重梯度的大小有影响。具体的，如在计算过程中对所有输入数据样本 xix_ixi 乘以 100，那么权重的梯度将会增大 100 倍，这样就必须降低学习率来弥补。

也说明了数据预处理有很重要的作用，它即使只是有微小变化，也会产生巨大影响。

对于梯度在计算线路中是如何流动的有一个直观的理解，可以帮助调试神经网络。

4) 复杂示例

我们来看一个复杂一点的例子：

f(w,x)=11+e−(w0x0+w1x1+w2)f(w,x) = \frac{1}{1+e^{-(w_0x_0 + w_1x_1 + w_2)}}f(w,x)=1+e−(w0x0+w1x1+w2)1

这个表达式需要使用新的门单元：

f(x)=1x→dfdx=−1x2 fc(x)=c+x→dfdx=1 f(x)=ex→dfdx=ex fa(x)=ax→dfdx=a\begin{aligned} f(x) &= \frac{1}{x} \ \rightarrow \frac{df}{dx} &=- \frac{1}{x^2}\ f_c(x) = c + x \ \rightarrow \frac{df}{dx} &= 1 \ f(x) = e^x \ \rightarrow \frac{df}{dx} &= e^x \ f_a(x) = ax \ \rightarrow \frac{df}{dx} &= a \end{aligned}f(x)→dxdf→dxdf→dxdf→dxdf=x1=−x21 fc(x)=c+x=1 f(x)=ex=ex fa(x)=ax=a

计算过程如下：

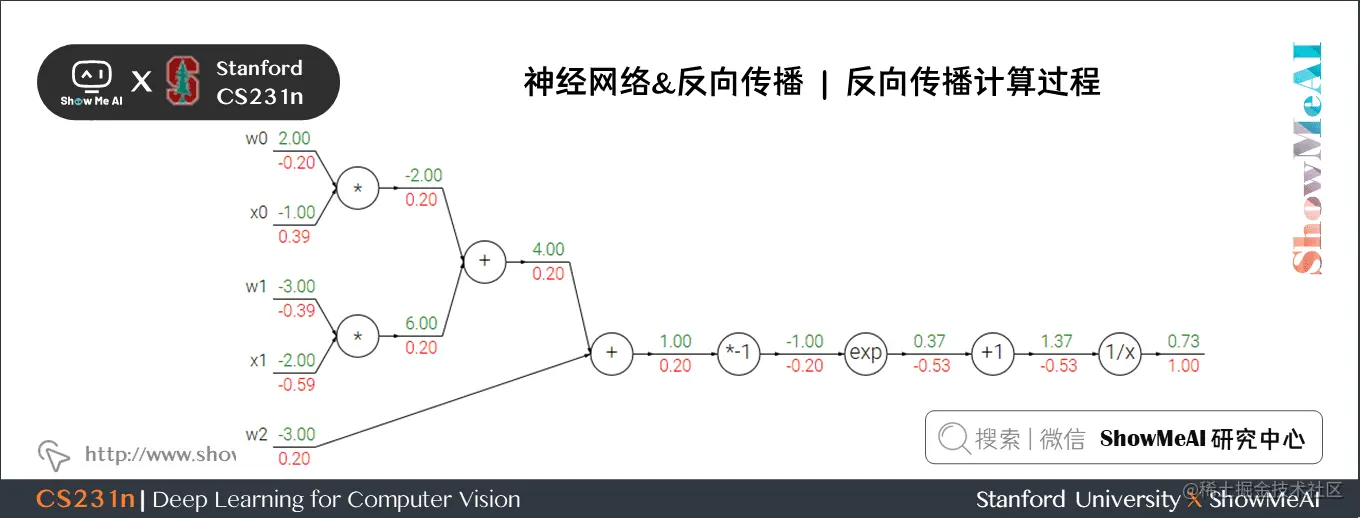
• 对于 1/x1/x1/x 门单元，回传梯度是 111，局部梯度是 −1/x2=−1/1.372=−0.53-1/x^2=-1/1.372=-0.53−1/x2=−1/1.372=−0.53 ，所以输入梯度为 1×−0.53=−0.531 \times -0.53 = -0.531×−0.53=−0.53；+1+1+1 门单元不改变梯度还是 −0.53-0.53−0.53
• exp门单元局部梯度是 ex=e−1e^x=e{-1}ex=e−1 ，然后乘回传梯度 −0.53-0.53−0.53 结果约为 −0.2-0.2−0.2
• 乘 −1-1−1 门单元会将梯度加负号变为 0.20.20.2
• 加法门单元会分配梯度，所以从上到下三个加法分支都是 0.20.20.2
• 最后两个乘法单元会转换梯度，把回传梯度乘另一个输入值作为自己的梯度，得到 −0.2-0.2−0.2、0.40.40.4、−0.4-0.4−0.4、−0.6-0.6−0.6

5) Sigmoid门单元

我们可以将任何可微分的函数视作「门」。可以将多个门组合成一个门，也可以根据需要将一个函数拆成多个门。我们观察可以发现，最右侧四个门单元可以合成一个门单元，σ(x)=11+e−x\sigma(x) = \frac{1}{1+e^{-x}}σ(x)=1+e−x1 ，这个函数称为 sigmoid 函数。

sigmoid 函数可以微分：

dσ(x)dx=e−x(1+e−x)2=(1+e−x−11+e−x)(11+e−x)=(1−σ(x))σ(x)\frac{d\sigma(x)}{dx} = \frac{e^{-x}}{(1+e{-x})^2} = \left( \frac{1 + e^{-x} - 1}{1 + e^{-x}} \right) \left( \frac{1}{1+e^{-x}} \right) = \left( 1 - \sigma(x) \right) \sigma(x)dxdσ(x)=(1+e−x)2e−x=(1+e−x1+e−x−1)(1+e−x1)=(1−σ(x))σ(x)

所以上面的例子中已经计算出 σ(x)=0.73\sigma(x)=0.73σ(x)=0.73 ，可以直接计算出乘 −1-1−1 门单元输入值的梯度为：1∗(1−0.73)∗0.73 =0.21 \ast (1-0.73) \ast0.73~=0.21∗(1−0.73)∗0.73 =0.2，计算简化很多。

上面这个例子的反向传播的参考 python 实现代码如下：

python复制代码# 假设一些随机数据和权重
w = [2,-3,-3] 
x = [-1