PCA 主成分分析法上

主成分分析（principal component analysis）主要用于降维和降噪。

PCA 的数学推导可以从最大可分型和最近重构性两方面进行，前者的优化条件为划分后方差最大，后者的优化条件为点到划分平面距离最小，本文将从方差最大可分性的角度进行分析。

提示：文章涉及到的公式推导都是基础的线性代数内容，静下心来可以看明白。

百度百科解释：

前言

我们需要对PCA有一个整体的认识：PCA 最重要的是求解一个新的空间（的基），然后利用这个新的空间坐标系进行降维。为什么要求解一个新的空间？主要为了降维。简单来说我们使用PCA降维就是把一个高维数据降到低维，但是这个过程有一个非常重要的步骤，就是寻找一个新的坐标系（新的空间基）

我们用一个二维数据来看一下如何找新的空间坐标系（或者找这个空间坐标系的标准是什么？）
假设有5个样本2个特征$X_{5\times 2}$，分布在二维平面上，在不改变坐标系的情况下，降维思想很自然的有2个。
1）将原始数据向$w_0$轴做投影（抛弃$w_1$轴的所有信息）
2）将原始数据向$w_1$轴做投影（抛弃$w_0$轴的所有信息）

以1）为例，我们让所有样本的$w_1=0$，这样一来我们就抛弃了$w_1$轴上的所有信息，那么原始数据就完成的一个最简单，粗暴的一个降维了，样本由原来的2个维度的特征表示，变成了1个维度的表示。可是这样我们就是损失了一整个维度的数据信息，但是为了降维我们不得不这样做。
下图左$w_0$和$w_1$轴上的点都是基于上面简单粗暴的降维思想完成的。

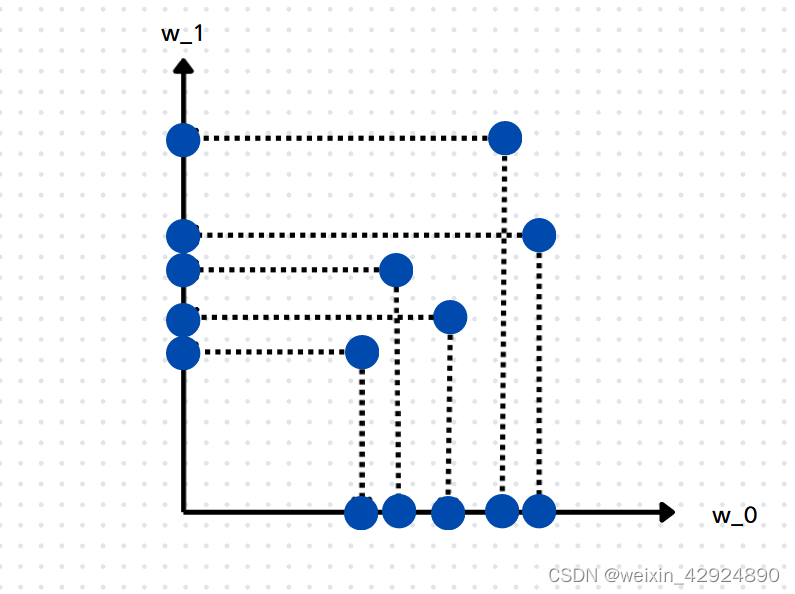
但是这样做是不是最好的呢？还有没有其他方法了呢?

从上面的思想我们可以借鉴，无非是把数据映射到某一条直线上（二维平面），如果我们把样本数据映射到这么一个直线上，使得我们损失的信息最少，也就是要保留的方差最大 这是我们最想要的结果，数据经过降维后尽可能的保留原始数据信息量。这个怎么处理？
注：上面黑体加粗也可以这样理解 映射到直线上的特征分布尽量和原始数据的分布保持一致

这里又一个问题，那就是数据映射到某一个直线上，想要损失的信息最少可以理解没问题，那他为什么等价保留的方差最大呢？我们来彻底扒开PCA神秘的面纱吧。

假设我们用一个向量的模来表示一个样本所含有的信息量，那么如下图，我故意将二维空间的坐标系画的有点倾斜，是向轴1做投影还是还是向轴2做投影，样本在将来降维的时候所保留的信息量最大呢，显然我们应该向轴1做投影比较好，其投影值和向量模最接近。对于所有的样本都这样做，降维后所保留的信息量也是最多的。

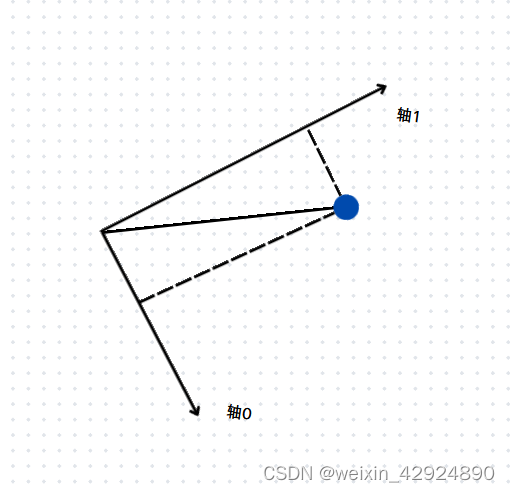
那这和方差有什么关系？有。一般我们都是希望一组数据的方差越小越好，方差的大小描述了一组数据在均值附近的离散程度。我们这里是反其道而行之，我们希望方差越大越好。假设数据两个维度的均值都为0，那么方差大，就意味着，两个数据分的更开，数据更具有区分度。方差公式 $s^2=\frac{{\sum }_i^n(x-\bar{x}{)}^2}{n}，x\in R$
如图，OA和OB是两个样本在轴1的投影值，均值为0时，两个样本分的更开，降维后的数据更具有区分度（实际上就是这2个数据向轴1做投影）。

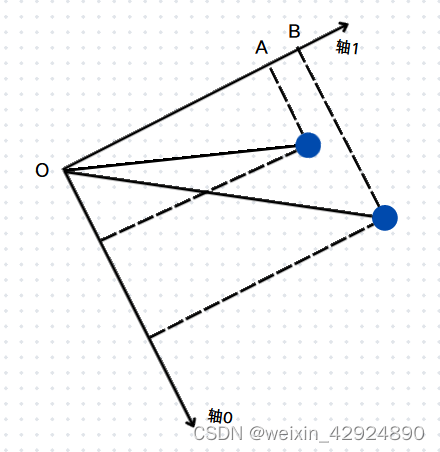
回到我们之前的例子里来，我们之前是将数据直接映射在老坐标系中，这样数据损失的信息太多了。现在我们可以找一条直线作为新坐标系的其中一条，让这5个数据点都垂直这条直线，也就是说找到了新坐标系中的一个轴，让这5个样本点到新轴的直线距离最小。由于在二维平面，一个坐标轴找到了，另外一个也就确定了。（这里的第一个轴也就是百度百科里说的第一主成分，第二个轴是第二主成分，所包含的信息是逐渐减少的，可以推广到高维）如图红色坐标系就是二维空间新的坐标系。

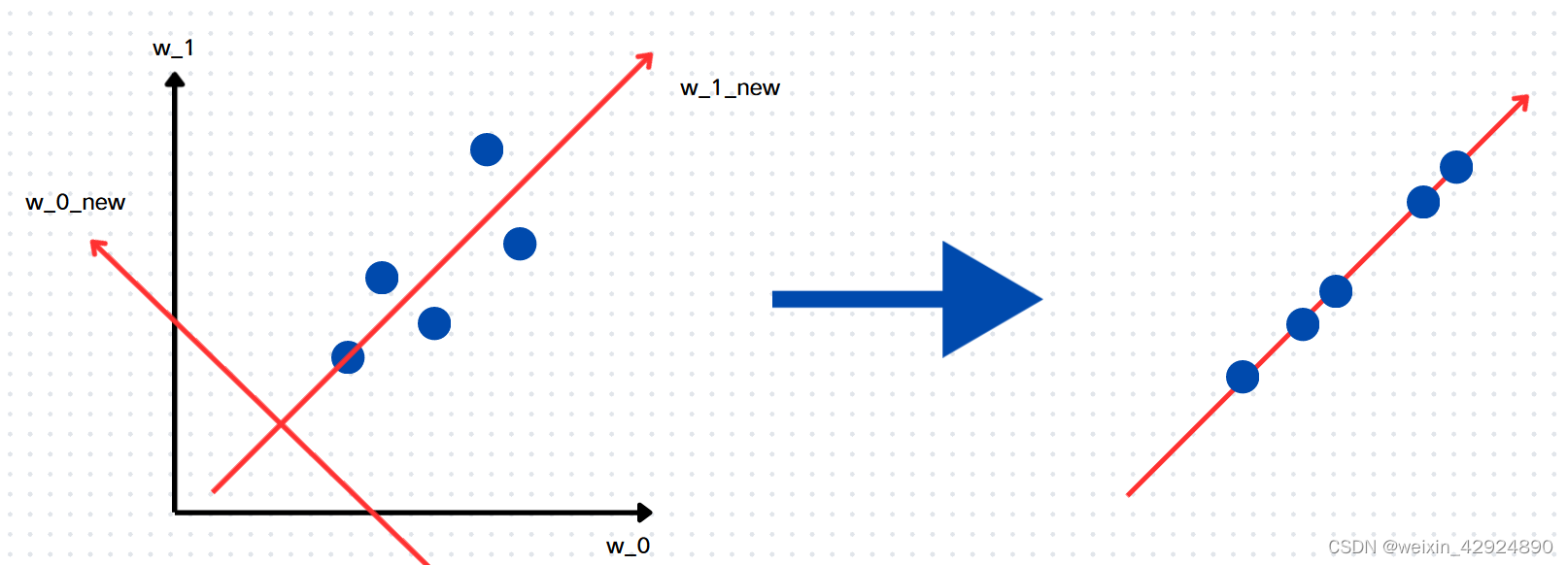
我们再来回顾一下上面的过程，PCA降维就是在原数据中找一个新的坐标系，将数据映射到第一个轴上保留的信息是最多的也就是第一主成分，然后再找第二个轴轴上信息递减（第二主成分），依次类推到高维。此时已经完成了二维空间找主成分的任务，还没有涉及到降维。

目标函数推导

上述问题中可以转化为，最大化所有映射到直线上数据的方差问题。这是一个最优化问题，可以用梯度上升法来求解（或其他方法）。

步骤：

1、对所有的样本数据进行demean处理，让所有数据的某一个维度的均值为0，demean操作是将整个数据的坐标轴进行平移，将坐标轴平移到数据中心位置，这样做的好处是在后面公式推导的时候可以简化计算。

2、假设我们要求第一个轴的方向向量为w。

3、所有的样本，映射到方向向量w后，所以方差计算公式

（注意这里是映射到直线后的数据，不是原始数据了。我们在进行从果到因的推导过程）

$$Var(X_{project})=\frac{1}{m}\sum _{i=1}^m(X_{project}^{(i)}-{\bar{X}}_{project}{)}^2$$

$X_{project}^{(i)}-{\bar{X}}_{project}$是每一样本减去每一个特征均值的向量，准确来说这里应该用范数的平方，即

$$Var(X_{project})=\frac{1}{m}\sum _{i=1}^m||X_{project}^{(i)}-{\bar{X}}_{project}|{|}^2$$

又因为数据已经去均值了，所以${\bar{X}}_{project}=0$，即

$$Var(X_{project})=\frac{1}{m}\sum _{i=1}^m||X_{project}^{(i)}|{|}^2$$

也就是找到一个轴（在二维平面你可以理解成直线或方向向量），使得所有数据映射到这个轴的方差最大，$||X_{project}^i|{|}^2$表示一个样本数据的方差。这里需要理解一下在高纬度空间为什么向量模的平方就是方差。

方差是要减去一个平均值的，但是我们已经将每个维度的值减去平均值了，准确来说${\bar{X}}_{project}$应该是一个零向量。假设$X_{project}^{(i)}$就是前言中的2个特征维度的数据，再次说明一下此时的数据是映射后的数据。
$$X_{project}^{(1)}表示第一个样本，即X_{project}^{(1)}=(w_0,w_1)$$
则：
$$\begin{array}{rl}{X}_{project}^{(1)}\cdot X_{project}^{(1)}& =\left|X_{project}^{(1)}\right|\cdot \left|X_{project}^{(1)}\right|\cdot \cos \alpha \\ & =\sqrt{w_0^2+w_1^2}\cdot \sqrt{w_0^2+w_1^2}\\ & =w_0^2+w_1^2\end{array}$$

在一维数据中均值如果为0，$x_i^2$表示某个样本的方差，在多维空间中假设每个特征的均值为零向量，由于一个样本有多个特征值，所以我们用每个特征值的平方再求和来表示样本的方差，即$||X^{(i)}|{|}^2$。

现在多维空间样本的方差我们知道了，那么最大化所有样本的方差就是我们的目标函数。
$$Var(X_{project})=\frac{1}{m}\sum _{i=1}^m||X_{project}^{(i)}|{|}^2$$
好了，到这里我们知道了一个均值为0向量的多维空间是如何求方差的了。既然是最优化一个函数，那么我们要求解的变量是什么？目前我们还不知道呢。

对于一个具体的函数问题，我们一般假设一个要求解的变量为$x$，这里我们要求解一个直线（可推导到高维空间，二维空间便于理解），假设那个直线用方向向量$w$来表示，则$w=(w_0,w_1)$。

引入方向向量$w$，那么$w$和$X^{(i)}$的内积如下，由于我们只需要求解一个直线的方向，所以我们将向量$w$的模长处理为1，则有下式成立，其中$\Vert X^{(i)}\Vert \cdot \cos \theta =\Vert X_{\text{project }}^{(i)}\Vert$，表示绿色直线的长度，也就是我们要求的向量。
$$\begin{array}{rl}& X^{(i)}\cdot w=\Vert X^{(i)}\Vert \cdot \Vert w\Vert \cdot \cos \theta \\ & X^{(i)}\cdot w=\Vert X^{(i)}\Vert \cdot \cos \theta \\ & X^{(i)}\cdot w=\Vert X_{\text{project }}^{(i)}\Vert \end{array}$$

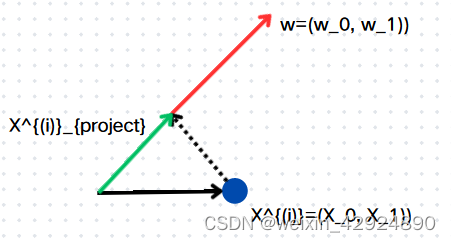
通过引入$w$单位方向向量，我们可以把上式目标函数转化下式，其中$X_{project}^{(i)}=X^{(i)}\cdot w$，目标向量就等价原始向量点乘一个单位方向向量，那么未知变量就来了，我们现在就是要把这个$w$向量求出来即可。

$$\begin{array}{rl}Var(X_{project})& =\frac{1}{m}\sum _{i=1}^m||X_{project}^{(i)}|{|}^2\\ & =\frac{1}{m}\sum _{i=1}^m||X^{(i)}\cdot w|{|}^2\end{array}$$
至此我们由结果出发，一步一步将要求的变量$w$引入了我们的目标函数中。

目标函数

求$w$向量，使下式最大，
$$\begin{array}{rl}Var(X_{project})& =\frac{1}{m}\sum _{i=1}^m{\left(X^{(i)}\cdot w\right)}^2\\ & =\frac{1}{m}\sum _{i=1}^m{\left(X_1^{(i)}{w}_1+X_2^{(i)}{w}_2+\cdots +X_n^{(i)}{w}_n\right)}^2\\ & =\frac{1}{m}\sum _{i=1}^m{\left(\sum _{j=1}^n{X}_j^{(i)}{w}_j\right)}^2\\ & X_{m\cdot n}表示m个样本n个特征,\\ & X_{1\times n}^{(i)}表示第i个样本数据,\\ & w_{n\times 1}表示要求解的未知向量。\end{array}$$
第二个等号和第三个等号只不过是将矩阵点乘拆开而已，两者是等价的，可以无视。

我们使用梯度上升法来解决这个目标函数的最优化问题。

梯度求解

为了简化，我们将上式写成， $$f(w)=\frac{1}{m}\sum _{i=1}^m{\left(X^{(i)}\cdot w\right)}^2$$自变量一个方向向量$w$，维度和原始数据特征维度一致。

梯度求导
$$\nabla f=\left(\begin{array}{c}\frac{\partial f}{\partial w_1}\\ \frac{\partial f}{\partial w_2}\\ \dots \\ \frac{\partial f}{\partial w_n}\end{array}\right)=\frac{2}{m}\left(\begin{array}{c}{\sum }_{i=1}^m\left(X_1^{(i)}{w}_1+X_2^{(i)}{w}_2+\dots +X_n^{(i)}{w}_n\right)X_1^{(i)}\\ {\sum }_{i=1}^m\left(X_1^{(i)}{w}_1+X_2^{(i)}{w}_2+\dots +X_n^{(i)}{w}_n\right)X_2^{(i)}\\ \dots \\ {\sum }_{i=1}^m\left(X_1^{(i)}{w}_1+X_2^{(i)}{w}_2+\dots +X_n^{(i)}{w}_n\right)X_n^{(i)}\end{array}\right)$$

整理成向量的形式
$$\nabla f=\frac{2}{m}\left(\begin{array}{c}{\sum }_{i=1}^m\left(X^{(i)}w\right)X_1^{(i)}\\ {\sum }_{i=1}^m\left(X^{(i)}w\right)X_2^{(i)}\\ \dots \\ {\sum }_{i=1}^m\left(X^{(i)}w\right)X_n^{(i)}\end{array}\right)=\frac{2}{m}\cdot X^T(Xw)$$
注意

$X^{(i)}w=X_1^{(i)}{w}_1+X_2^{(i)}{w}_2+\dots +X_n^{(i)}{w}_n{X}^{(i)}表示一个1\times n的样本数据，有n个特征，w是n\times 1的待求向量$

这里为什么要将$X_{\mathrm{1...}n}^{(i)}$转置后放到前面，可以参考文尾链接，后面有打算再整理一下这块知识。假设我们现在知道是这么做的。实在着急的小伙伴可以根据维度理解一下。

现在梯度有了，由于是求最大化目标函数，所以$w$的更新为：
$$w=w+\eta \nabla f$$

代码实现

构造一个含有一定线性相关的数据集，demean是去除数据每一个维度的均值。代码最后可以看到数据每一个维度的均值都为0。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

X = np.empty((100, 2))
X[:, 0] = np.random.uniform(0., 100., size=100)
X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 10., size=100)


plt.scatter(X[:, 0], X[:, 1])
plt.show()

def demean(X):
    """ 原始数据 - 所有样本每一个维度的均值"""
    return X - np.mean(X, axis=0)


X_demean = demean(X)
plt.scatter(X_demean[:,0], X_demean[:,1])
plt.show()

print(np.mean(X_demean[:,0])) # -1.1652900866465642e-1
print(np.mean(X_demean[:,1])) # 1.4850343177386093e-14

原始数据图像，注意坐标轴原点
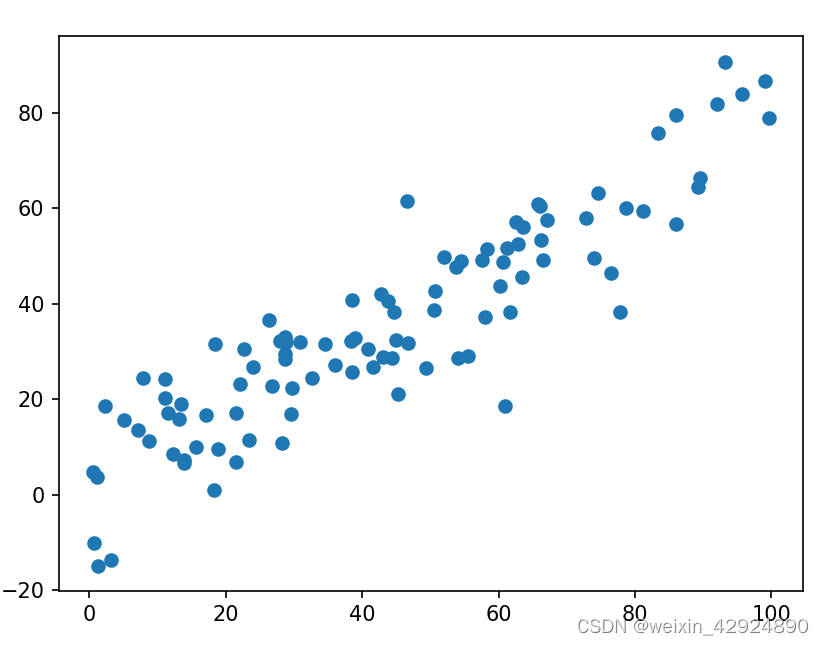demean数据图像，注意坐标轴原点

梯度上升法求解w向量

函数 f 是目标函数，所有映射到方向向量$w$上的数据方差和，即 $\frac{1}{m}{\sum }_{i=1}^m{\left(X^{(i)}\cdot w\right)}^2$；函数 df 是当前$w$下的梯度值；函数 gradient_ascent 是梯度上升法实现。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

X = np.empty((100, 2))
X[:, 0] = np.random.uniform(0., 100., size=100)
X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 10., size=100)


def demean(X):
    """ 原始数据 - 所有样本每一个维度的均值"""
    return X - np.mean(X, axis=0)


def f(w, X):
    """ 目标函数
    公式:\frac{1}{m} \sum_{i=1}^{m}\left(X^{(i)} \cdot w\right)^2
    """
    return np.sum((X.dot(w) ** 2)) / len(X)


def df(w, X):
    """ 目标函数的梯度，根据公式直接计算
    公式:\nabla f=\frac{2}{m} \cdot X^T(X w)
    """
    return X.T.dot(X.dot(w)) * 2. / len(X)


def direction(w):
    """向量单位化，用向量除以向量的模"""
    return w / np.linalg.norm(w)


def gradient_ascent(df, X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
    """ 梯度上法求解变量 w
    :param df ndarray: 某一个参数w下的梯度
    :param X ndarray: 经过demean的原始数据
    :param eta float: 学习率
    """
    # 向量单位化
    w = direction(initial_w)
    cur_iter = 0

    while cur_iter < n_iters:
        # 求梯度
        gradient = df(w, X)
        last_w = w
        # 更新参数
        w = w + eta * gradient
        # 方向向量单位化
        w = direction(w)
        # 计算误差，当前参数w的函数和上一个参数last_w的函数值差
        if (abs(f(w, X) - f(last_w, X)) < epsilon):
            break

        cur_iter += 1

    return w


# initial_w不能用0向量开始，不然梯度无法更新
initial_w = np.random.random(X.shape[1])
# 学习率
eta = 0.001
X_demean = demean(X)
w = gradient_ascent(df_math, X_demean, initial_w, eta)
print(w) # [0.7891932  0.61414501]
plt.scatter(X_demean[:, 0], X_demean[:, 1])
# w是一个单位向量，每个分量的值太小，这里放大了50倍
plt.plot([0, w[0] * 50], [0, w[1] * 50], color='r')
plt.show()

# 调用sklearn中PCA包用于验证
pca = PCA(n_components=1)
# pca降维
pca.fit(X)
# 输出具有最大方差的成分，也就是第一主成分
print(pca.components_) # [[0.78919356 0.61414455]]

下图红色直线是我们根据梯度上升法求解的$w$向量。
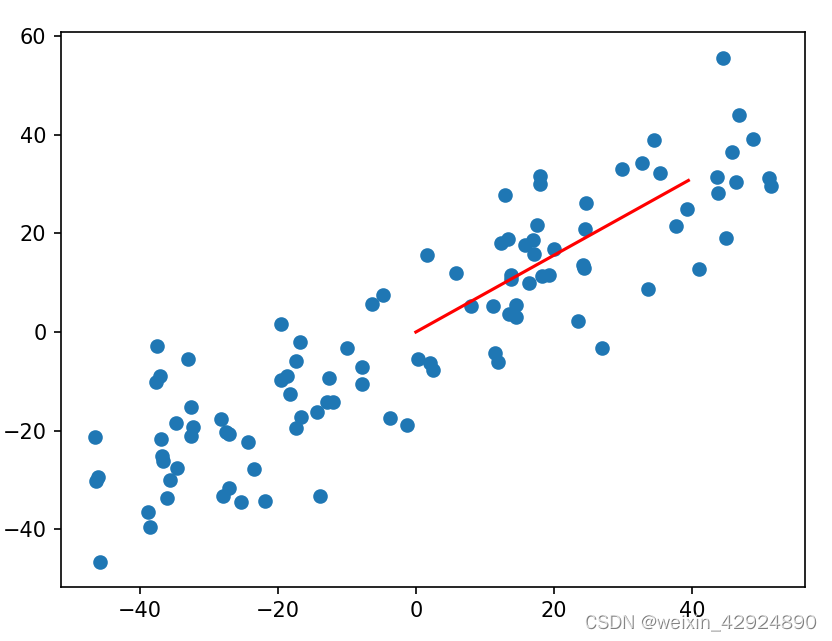最后通过调用sklearn中PCA的实现，可以发现我们自己的代码是没有问题的。

结果如下：有时候sklearn求出的向量和我们自己实现的结果方向相反，这是没有问题的。

# [0.7891932  0.61414501] # 通过梯度上升求解的第一主成分
# [[0.78919356 0.61414455]] # 通过sklearn求解的第一主成分

总结

在本文中我们通过一个优化目标函数的推导过程，利用梯度上升法求解了目标函数的一组参数$w$，通过代码实现我们可以知道求解的是二维空间数据的第一主成分。但请记住我们还没有真正实现PCA的降维，仅仅是针对二维数据求出第一主成分，也就是方差最大的那个轴（二维空间中新坐标轴的一个轴）。我们还遗留了一些问题。

1）对于一个维度非常高的数据，不可能只取第一主成分，假设我们要取前$k$个成分，如何处理呢？

2）到目前为止实现真正的PCA还要多久？让我们看一下篇文章吧。

参考：

知乎高赞pca梳理 https://zhuanlan.zhihu.com/p/77151308

sklearn中pac使用 https://blog.csdn.net/m0_43405302/article/details/123594788

矩阵向量求导链式法则 https://www.cnblogs.com/pinard/p/10825264.html