【李航-统计学习方法】第五章- 决策树-2

5.2 特征选择

5.2.１ 特征选择问题

如前述所讲，特征选择在于选取对训练数据具有分类能力的特征。
如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征是没有分类能力的。（这个定义…）
故扔掉没有分类能力的该类特征对决策树学习的精度影响不大。
特征选择的准则是信息增益或信息增益比。

例 5.1
说明：数据是一个由15个样本组成的贷款申请训练数据，数据包括贷款申请人的4个特征（属性）。
特征和属性是不一样的，
一个特征（属性）有三个特征值，但总共有四个特征。
注意区别：特征（属性）与特征值。（有助于理解信息增益的算法）

目的： 希望通过所给的训练数据学习一个贷款申请的决策树，用以对未来的贷款申请进行分类，即当新的客户提出贷款申请时，根据申请人的特征利用决策树决定是否批准贷款申请。
重点： 特征选择是决定用哪个特征来划分特征空间。

我们从表5.1数据学习到的两个可能的决策树，分别由两个不同特征（年龄和有工作）的根结点构成。两个决策树都可以从此延续下去。

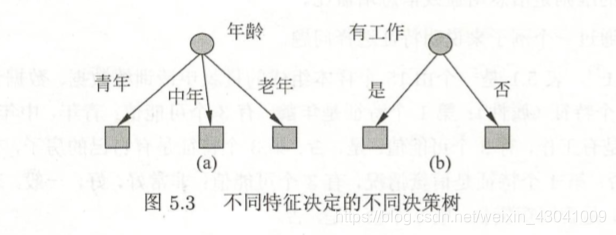
问题是：究竟选择哪个特征更好些？这需要确定选择特征的准则。
信息增益（information gain）即表示这一直观的准则。

5.2.２ 信息增益

(1)熵

为了便于说明，先给出熵与条件熵的定义。
在信息论与概率统计中，熵（entropy）是表示随机变量不确定性的度量。设$X$是一个取有限个值得离散随机变量，其概率分布为：
$$P(X=x_i)=p_i,i=1,2,...,n$$
则随机变量$X$的熵的定义为：
$$H(X)=-\sum _{i=1}^n{p}_{i}log{p}_i\text{\hspace{1em}(5.1)}$$
在式（5.1）中，若$p_i=0$,则定义0log0=0.通常，式（5.1）中的对数以2为底或以e为底（自然对数），这时熵的单位分别称作比特（bit）或者纳特（nat）。由定义可知，熵只依赖于$X$的分布，而与$X$的取值无关，所以也可将$X$的熵记作$H(p)$，即
$$H(p)=-\sum _{i=1}^n{p}_{i}log{p}_i$$