论文笔记 SCAFFOLD Stochastic Controlled Averaging for Federated Learning

论文题目：《SCAFFOLD Stochastic Controlled Averaging for Federated Learning》

论文地址：https://arxiv.org/pdf/1910.06378.pdf
 

Abstract

FedAvg ：简单、低通行成本 --> 联邦学习首选算法

But！数据异构（non-IID）时， FedAvg 会遭受“客户端漂移”，从而导致收敛不稳定和缓慢。

解决方案：新算法 SCAFFOLD，使用 控制变量（方差减少） 来校正其本地更新中的“客户端漂移”。

SCAFFOLD 的改进效果：

• SCAFFOLD 需要的通信轮次明显减少
• 不受数据异构性或客户端采样的影响
• 可以利用客户端数据的相似性，从而产生更快的收敛（量化分布式优化中局部步骤有用性的第一个结果）

 

1. Introduction

联邦学习已成为现代大规模机器学习的一种重要范例。

联邦学习 VS 传统的集中式学习：

• 集中式学习：使用存储在中央服务器中的大型数据集进行模型训练
• 联邦学习：训练数据仍然分布在大量客户端上（这些客户端可能是电话、网络传感器、医院，或替代本地信息源），在本地训练模型，无需通过网络传输客户端数据，从而确保基本的隐私级别。

本文研究了用于联邦学习的随机优化算法。

联邦优化的关键挑战是：

• 处理服务器和客户端之间不可靠且相对较慢的网络连接。

• 在给定时间只有一小部分客户端可用于训练。

• 不同客户端上存在的数据存在很大的异质性（non-IId）。

  FedAvg 解决通信瓶颈方法：在与服务器通信之前对可用客户端执行多个本地更新。尽管它在某些应用中取得了成功，但其在异构数据上的性能仍然是一个活跃的研究领域。

  本文证明了这种异质性确实对 FedAvg 有很大的影响，它在每个客户端的更新中引入了 client-drift 客户端漂移，导致收敛缓慢、不稳定。

  即使使用了全批次梯度，并且所有客户端都参与了整个训练，这种客户漂移仍然存在。

 

解决方案：提出了一种新的随机控制平均算法（SCAFFOLD），试图纠正这种客户端漂移。

直观地说，SCAFFOLD 估计了服务器模型的更新方向 c 和每个客户端的更新方向 ci 。差值 （c − ci） 是用于校正本地更新的客户端漂移的估计。该策略成功地克服了异质性，并在显著减少的通信成本中收敛。或者，可以将异质性视为在不同客户端的更新中引入“客户端差异”，然后 SCAFFOLD 执行 “客户端差异减少”。使用这个观点来表明 SCAFFOLD 相对不受客户端采样的影响。

client sampling：客户端采样。采样就是只选择一部分，客户端采样就是选择一部分客户端。

尽管适应异质性很重要，但利用客户端数据中的相似性同样重要，SCAFFOLD 就有这样的特性：客户端越相似，需要的通信越少。

 

贡献：

• 推导出 FedAvg 的收敛速度比之前已知的具有客户端采样和异构数据的凸函数和非凸函数的收敛速度更快。

• 给出了匹配下限，以证明：即使没有客户端采样，使用全批次梯度，FedAvg 的收敛速度也可能因为客户端漂移比 SGD 慢。

• 提出了一种新的随机控制平均算法（SCAFFOLD），用于校正这种客户端漂移。

  证明了 SCAFFOLD 的收敛速度至少与 SGD 一样快，并且可以收敛于任意异构数据。

• 表明 SCAFFOLD 可以利用客户端之间的相似性，进一步减少所需的通信，首次证明了采取本地步骤优于大批量 SGD 的优势。

• 证明 SCAFFOLD 相对不受客户端采样的影响，从而获得方差降低率，使其特别适用于联邦学习。

最后，在模拟和真实数据集上证实了理论结果。

 

2. Setup

将问题形式化为最小化随机函数的和，只访问随机样本。

符号定义：

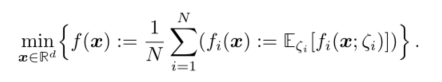
函数 $f_i$ 表示客户端 $i$ 上的损失函数（本文所有结果都可以很容易地扩展到加权情况）

假设 $f$ 从下面有界于 $f^{\ast }$，并且 $f_i$ 是 β-光滑的。此外，假设 $g_i(x):=\nabla f_i(x;{\zeta }_i)$ 是 $f_i$ 的无偏随机梯度，方差以 ${\sigma }^2$ 为界。对于某些结果，假设 $\mu \ge 0$（强）凸性。注意，$\sigma$ 仅限制客户端内的方差。

定义以下两个非标准术语：

（A1） (G,B)-BGD 或 有界梯度不相似性：

存在常数 $G\ge 0$ 和 $B\ge 1$ 使得

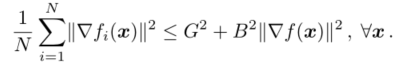
如果 $f_i$ 是凸的，可以将假设放宽到

（A2）δ-BHD 或 有界Hessian差异：

此外，$f_i$ 是 δ-弱凸的，即 ${\nabla }^2{f}_i(x)⪰-\delta I$。

假设A1和A2是正交的，有可能 $G=0$ 和 $\delta =2\beta$，或者 $\delta =0$ 但 $G>>1$。

Hessian：黑塞矩阵，是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。

 

3. Convergence of FedAvg

本节回顾 FedAvg ，并通过推导出比以前更严格的收敛速度来改进其收敛性分析。

FedAvg 笔记可见：https://blog.csdn.net/weixin_43235581/article/details/127427921

FedAvg 包括两个主要部分：

• 对模型的本地更新
• 聚合客户端更新以更新服务器模型

首先，在每一轮中，客户端的子集 $S\subseteq [N]$ 均匀采样，每个客户 $i\in S$ 复制当前服务器模型 $y_i=x$，并执行 $K$ 次本地更新：

${\eta }_l$ 为局部步长（学习率）

其次，客户端的更新 $(y_i-x)$ 使用全局步长 ${\eta }_g$ 聚合以形成新的服务器模型：

 

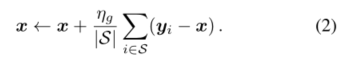
3.1. 收敛速度

具有有界不相似性的函数的新收敛结果：

定理 I. 对于满足（A1）的 β-光滑函数 { $f_i$}，FedAvg 的输出期望误差小于 $ϵ$ 的某些值 ${\eta }_l、{\eta }_g、R$ 满足：

（强凸、一般凸、非凸）

将 FedAvg 的收敛速度与更简单的 IID 情况（例如 G=0 和 B=1）进行比较是很有启发性的。

FedAvg 的强凸率为 $\frac{{\sigma }^2}{\mu SKϵ}+\frac{1}{\mu }$。相比之下，此前已知的最佳速率是 σ 2 µ