TBB-Note-Algo-parallel_scan

cracker:)

已于 2025-05-18 07:55:35 修改

阅读量934

点赞数 15

分类专栏： TBB 文章标签： c++

于 2025-05-17 21:56:11 首次发布

本文链接：https://blog.csdn.net/weixin_43300611/article/details/147806001

版权

TBB 专栏收录该内容

8 篇文章

订阅专栏

TBB学习笔记八（[Algorithms.parallel_scan]）

《Today’s TBB 2nd Edition》

parallel_scan

扫描，虽然不常见，但也是很重要的算法。它又被称为前缀和（prefix），类似于归约，其核心是为输入序列中的每个元素生成累积结果，同时保留中间状态。扫描操作对输入序列 $x_0, x_1, ..., x_n$ 进行逐元素累积计算，生成两个结果：
（1）中间结果：每个位置的累积值 $y_0, y_1, ..., y_n$ （如 $y_i = x_0 + x_1 + ... + x_i$ ）；
（2）最终结果：最后一次累积的总值 $y_n$ 。

tbb::parallel_scan是一个函数模板，其中的一个典型的函数签名如下。

template<typename Range, typename Value, typename Scan, typename ReverseJoin>
    __TBB_requires(tbb_range<Range> && parallel_scan_function<Scan, Range, Value> &&
                   parallel_scan_combine<ReverseJoin, Value>)
Value parallel_scan( const Range& range, const Value& identity, const Scan& scan, const ReverseJoin& reverse_join );

Range：数据的输入范围，需要满足TBB的范围概念；
Value：累加结果的类型；
Scan：二元操作函数；
ReverseJoin：合并函数。

Case 1

看一个计算数组元素前缀和的例子。

int simpleSerialRunningSum(const std::vector<int>& v, std::vector<int>& rsum) {
  int N = v.size();
  rsum[0] = v[0];
  for (int i = 1; i < N; ++i) {
    rsum[i] = rsum[i-1] + v[i];
  }
  int final_sum = rsum[N-1];
  return final_sum;
}

表面上看，扫描看着是一个串行算法，每一个前缀和都依赖所有先前迭代中的结果。而tbb::paralllel_scan可以高效地并行实现这个过程。在并行扫描中，扫描体（scan body）可能对同一数据块执行多次操作：第一次在预扫描（pre-scan）模式以及后续的最终扫描模式（final-scan）模式。

pre-scan：接受一个不完整的前缀结果，仅代表前面某个自范围的结果，并且返回的是部分的前缀值。换句话说，预扫描计算的是局部和，可能这个结果尚未包含所有前置块的总和；
final-scan：接受完整的前缀结果，合并成准确的最终结果。
这样的一种并行化的过程如图所示。数组分成三个chunk： $A ， B ， C$ 。先计算 $A$ 的时候，由于 $A$ 是首个数据集，所以它的前缀和是精确的，即为identity value。而对于 $B$ ，分为两个模式计算，pre-scan模式计算不依赖于前缀和的部分， $B$ 的pre-scan和 $A$ 是并行的，另一模式final-scan组合 $A$ 的final-scan模式的结果和 $B$ 的pre-scan模式的结果，以此作为 $C$ 前缀的精确结果。在这个例子下，对于 $B$ ，校准的结果来自与 $A$ ，对于 $C$ ，校准的结果来源自 $A$ 的final-scan和 $B$ 的pre-scan。相对于串行执行的过程，以pre-scan和final-scan的并行过程确是明智之举。而且如果我们至少有两个核心，并且 $N$ 足够大，那么使用三个块的并行前缀和可以在顺序实现的三分之二时间内计算出来。

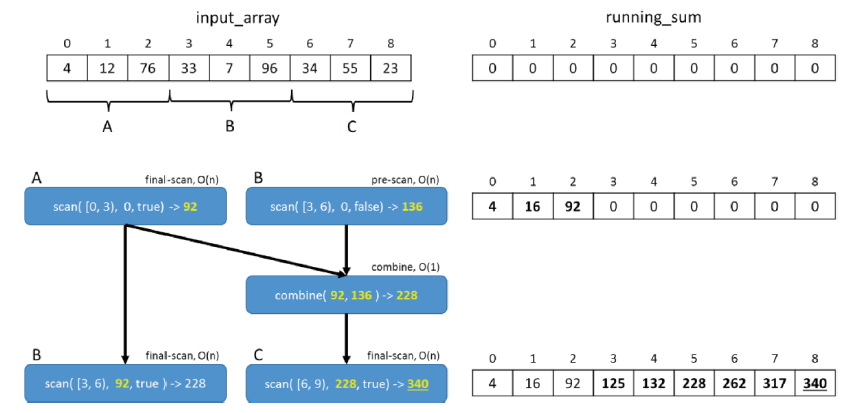
使用tbb::parallel_scan实现如下。

int simpleParallelRunningSum(const std::vector<int>& v, std::vector<int>& rsum) {
  int N = v.size();
  rsum[0] = v[0];
  int final_sum = tbb::parallel_scan(
    /* range = */ tbb::blocked_range<int>(1, N), 
    /* identity = */ (int)0,
    /* scan body */ 
    [&v, &rsum](const tbb::blocked_range<int>& r, 
                int sum, bool is_final_scan) -> int {
      for (int i = r.begin(); i < r.end(); ++i) {
        sum += v[i];
        if (is_final_scan) 
          rsum[i] = sum;
      }
      return sum;
    },
    /* combine body */
    [](int x, int y) {
      return x + y;
    }
  );
  return final_sum;
}

Case 2

再看一个稍微复杂的例子：基于视线角度的可见性分析。
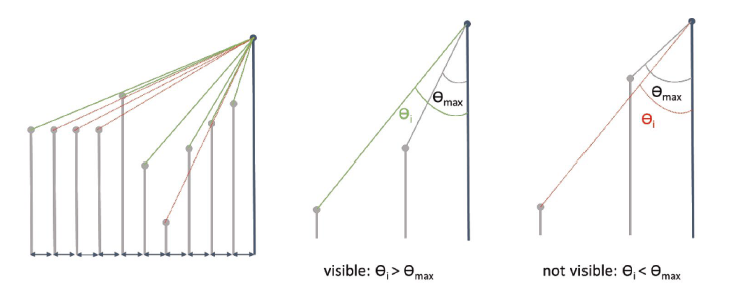
在这里插入图片描述
串行代码如下：

void serialLineOfSight(const std::vector<double>& altitude, 
                       std::vector<bool>& is_visible, double dx) {
  const int N = altitude.size();
  double max_angle = std::atan2(dx, altitude[0] - altitude[1]);
  double my_angle = 0.0;

  for (int i = 2; i < N; ++i ) {
    my_angle = std::atan2(i * dx, altitude[0] - altitude[i]);
    if (my_angle >= max_angle) {
      max_angle = my_angle;
    } else {
      is_visible[i] = false;
    }
  }
}

判断观察点 $a l t i t u d e [0]$ 到 $a l t i t u d e [n - 1]$ 可见性。逻辑是若目标点与观察点间存在更高仰角的中间点，则目标不可见。对于每个目标点 $i$ ，计算观察点的最大可见叫 $\theta_i$ :
$\theta_i =\text{ arctan} { \frac {altitude_0 - altitude_1} {d_i}}，$ 其中， $a l t i t u d e$ 各目标点的垂直高度， $d x$ 为水平距离增量。
在这个例子中在每个观察点都需要计算可见角度，且需要记录所有观察点的可见标记。 $max\_angle$ 需要在pre-scan和final-scan中计算。并行代码如下。

void parallelLineOfSight(const std::vector<double>& altitude, std::vector<bool>& is_visible, double dx) {
  const int N = altitude.size();
  
  double final_max_angle = tbb::parallel_scan(
    /*  range = */ tbb::blocked_range<int>(1, N), 
    /* identity */ 0.0,
    /* scan body */
    [&altitude, &is_visible, dx](const tbb::blocked_range<int>& r, 
                                 double max_angle, 
                                 bool is_final_scan) -> double {
      for (int i = r.begin(); i != r.end(); ++i) {
        double my_angle = atan2(i*dx, altitude[0] - altitude[i]);
        if (my_angle >= max_angle)
          max_angle = my_angle;
        if (is_final_scan && my_angle < max_angle)
          is_visible[i] = false;
      }
      return max_angle;
    },
    [](double a, double b) -> double {
      return std::max(a,b);
    } 
  );
}

范围划分：tbb::blocked_range<int>(1, N)将地形点划分为多个连续子区间（第 $1$ 个点到第 $N - 1$ 个点）。
扫描体：计算仰角：对每个点 $i$ ，计算其相对于起始点的仰角 $my\_angle$ ，使用std::max合并不同子区间的最大角度，确保全局最大角度的正确性。
tbb::parallel_scan的设计还是很精妙的。尽管这个过程还是将大规模数据分割为独立单元通过多线程/节点并行处理，但是巧妙地pre-scan和final-scan这样的解耦逻辑与缓存优化，将看似串行的工作拆解，在串行的动下追求同步的静，可谓动静等观。