【算法学习】隐马尔可夫模型HMM（例题+代码）

已于 2022-11-30 12:42:25 修改
阅读量7.7k 收藏 95
点赞数 15
文章标签： python 数据分析
于 2021-11-30 19:54:35 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_43316345/article/details/121640560
版权

隐马尔可夫模型HMM

介绍了模型的基本知识，和三个基本问题。其中对概率计算问题和预测（解码）问题进行了详细分析，并提供了python代码实现

公众号关注 52DATA ，获得更多数据分析知识,感谢支持—>

文章目录

一、题目引入

假设有三个盒子，每个盒子里都装有红白两种颜色的球，盒子里的红白球数由下表1列出
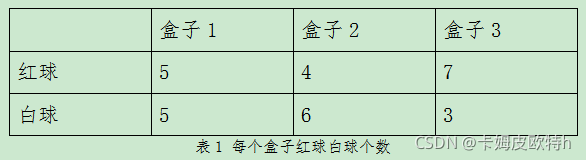
在这里插入图片描述
根据上表1，可以知道每次球出自于哪个盒子的概率，如表2：
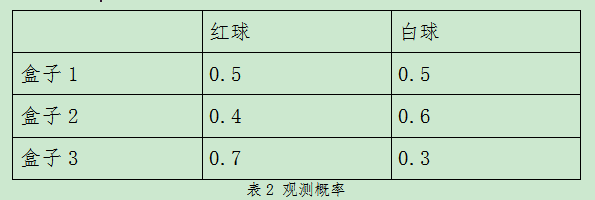
在这里插入图片描述
按照下面的方法抽球：开始，以(0.2,0.4,0.4)的概率随机选取 1 个盒子(假设已知，第一次在盒子1抽取球的概率为0.2，第一次在盒子2中抽取球的概率为0.4，第一次在盒子3中抽取球的概率为0.4)，然后从这个盒子里随机抽出 1 个球，记录其颜色后，放回；然后，从当前盒子随机转移到下一个盒子（这个概率假设已知，如表3），继续抽球，放回…,但是这个过程不知道从哪个盒子里抽取的，只能看到球的颜色。

已知t时刻选择的盒子为a,下一刻选中盒子a,b,c的概率为：
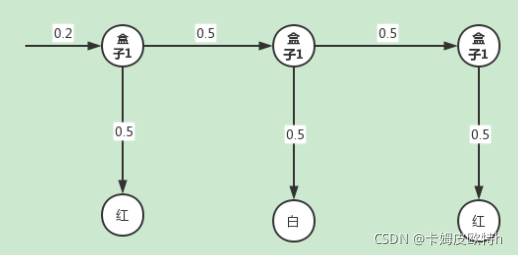
在这里插入图片描述

假设抽三次，抽取的结果为红球、白球、 红球，则该过程的流程图如下图：
在这里插入图片描述
也就是我抽取完球之后，只能看到球的颜色，但我不知道球来自取哪里，于是上面的灰色叫为隐状态，下面叫为观测状态。上述过程就叫做隐马尔科夫模型(HMM)

二、隐马尔科夫的基本概念

1.隐状态集合Q和可观测状态集合V

Q是所有可能的状态的集合（隐状态集合）
Q={}，N是可能的状态数
V是所有可能的观测的集合（可观测状态集合）
在这里插入图片描述，M是可能的观测数
注：集合里面的元素不能重复

2.状态序列I 和观测序列O

I 是长度为T 的状态序列，O 是对应的观测序列．
在这里插入图片描述

3.状态转移概率矩阵A

在这里插入图片描述

4.观测概率矩阵B

在这里插入图片描述

5.初始状态概率向量π

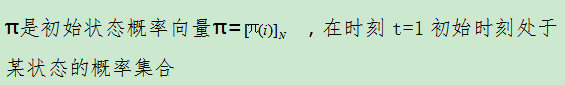
在这里插入图片描述

6.隐马尔科夫模型的三要素

隐马尔可夫模型由初始状态概率向量π、状态转移概率矩阵 A 和观测概率矩阵 B 决定．π和 A 决定状态序列，B 决定观测序列．因此，隐马尔可夫模型λ可以用三元符号表示，即λ=(A,B,π).A,B,π叫做隐马尔科夫模型的三要素。

7.隐马尔可夫模型的两个基本假设

(1)齐次马尔可夫性假设

即假设隐藏的马尔可夫链在任意时刻 t 的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻 t 无关．
在这里插入图片描述
在这里插入图片描述

(2)观测独立性假设

即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关．
在这里插入图片描述
在这里插入图片描述

三、将第一个问题用符号表示

隐藏状态集合Q={盒子1，盒子2，盒子3}，N=3
观测状态集合V={红，白}，M=2
在这里插入图片描述
假设总共摸了三次球，依次是红球，白球，红球，则
观测序列O={红，白，红}
但状态序列I 是不固定的，可能的取值有27种

1: 盒子1-->盒子1-->盒子1
2: 盒子1-->盒子1-->盒子2
3: 盒子1-->盒子1-->盒子3
......
25: 盒子3-->盒子3-->盒子1
26: 盒子3-->盒子3-->盒子2
27: 盒子3-->盒子3-->盒子3

四、隐马尔科夫的三个基本问题

在这里插入图片描述
在这里插入图片描述

(一)概率计算问题（例题+代码实现）

在这里插入图片描述

1.直接计算

在这里插入图片描述
公式看的太难了，以我们的例子来看，实际上就是穷举出所有情况出现的概率求和

盒子1 --> 盒子1 --> 盒子1    0.2*0.5*0.5*0.5*0.5*0.5 
盒子1 --> 盒子1 --> 盒子2    0.2*0.5*0.5*0.5*0.2*0.4 
盒子1 --> 盒子1 --> 盒子3    0.2*0.5*0.5*0.5*0.3*0.7 
盒子1 --> 盒子2 --> 盒子1    0.2*0.5*0.2*0.6*0.3*0.5 
盒子1 --> 盒子2 --> 盒子2    0.2*0.5*0.2*0.6*0.5*0.4 
盒子1 --> 盒子2 --> 盒子3    0.2*0.5*0.2*0.6*0.2*0.7 
盒子1 --> 盒子3 --> 盒子1    0.2*0.5*0.3*0.3*0.2*0.5 
盒子1 --> 盒子3 --> 盒子2    0.2*0.5*0.3*0.3*0.3*0.4 
盒子1 --> 盒子3 --> 盒子3    0.2*0.5*0.3*0.3*0.5*0.7 
盒子2 --> 盒子1 --> 盒子1    0.4*0.4*0.3*0.5*0.5*0.5 
盒子2 --> 盒子1 --> 盒子2    0.4*0.4*0.3*0.5*0.2*0.4 
盒子2 --> 盒子1 --> 盒子3    0.4*0.4*0.3*0.5*0.3*0.7 
盒子2 --> 盒子2 --> 盒子1    0.4*0.4*0.5*0.6*0.3*0.5 
盒子2 --> 盒子2 --> 盒子2    0.4*0.4*0.5*0.6*0.5*0.4 
盒子2 --> 盒子2 --> 盒子3    0.4*0.4*0.5*0.6*0.2*0.7 
盒子2 --> 盒子3 --> 盒子1    0.4*0.4*0.2*0.3*0.2*0.5 
盒子2 --> 盒子3 --> 盒子2    0.4*0.4*0.2*0.3*0.3*0.4 
盒子2 --> 盒子3 --> 盒子3    0.4*0.4*0.2*0.3*0.5*0.7 
盒子3 --> 盒子1 --> 盒子1    0.4*0.7*0.2*0.5*0.5*0.5 
盒子3 --> 盒子1 --> 盒子2    0.4*0.7*0.2*0.5*0.2*0.4 
盒子3 --> 盒子1 --> 盒子3    0.4*0.7*0.2*0.5*0.3*0.7 
盒子3 --> 盒子2 --> 盒子1    0.4*0.7*0.3*0.6*0.3*0.5 
盒子3 --> 盒子2 --> 盒子2    0.4*0.7*0.3*0.6*0.5*0.4 
盒子3 --> 盒子2 --> 盒子3    0.4*0.7*0.3*0.6*0.2*0.7 
盒子3 --> 盒子3 --> 盒子1    0.4*0.7*0.5*0.3*0.2*0.5 
盒子3 --> 盒子3 --> 盒子2    0.4*0.7*0.5*0.3*0.3*0.4 
盒子3 --> 盒子3 --> 盒子3    0.4*0.7*0.5*0.3*0.5*0.7

以上式子求和P(O|λ)=0.130218

画两个流程图就能明白了
盒子1 --> 盒子1 --> 盒子1 ：
在这里插入图片描述
盒子2 --> 盒子1 --> 盒子3：
在这里插入图片描述
但是直接求解太麻烦了，需要穷举出所有的情况，所以一般采用前向算法或后向算法

Python代码实现–直接求法

A=np.array([[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]])
B=np.array([[0.5,0.5],[0.4,0.6],[0.7,0.3]])
pai=np.array([0.2,0.4,0.4])

sum=0
for i in range(len(Q)):
    for j in range(len(Q)):
        for k in range(len(Q)):
            sum=sum+pai[i]*B[i][0]*A[i][j]*B[j][1]*A[j][k]*B[k][0]
            #print(Q[i],"-->",Q[j],"-->",Q[k],("%s*%s*%s*%s*%s*%s ")%(pai[i],B[i][0],A[i][j],B[j][1],A[j][k],B[k][0]),pai[i]*B[i][0]*A[i][j]*B[j][1]*A[j][k]*B[k][0])
            print(Q[i],"-->",Q[j],"-->",Q[k],"  ",("%s*%s*%s*%s*%s*%s ")%(pai[i],B[i][0],A[i][j],B[j][1],A[j][k],B[k][0]))


print("P(O|λ)=",sum)

2.前向算法

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
python代码实现–前向算法

Q=["box1","box2","box3"]#状态集合
V=["红","白"] #观测集合
#O=["红","白","红"]  #观测序列
O=[0,1,0] #转为数字类型,0代表红，1代表白
A=np.array([[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]])
B=np.array([[0.5,0.5],[0.4,0.6],[0.7,0.3]])
pai=np.array([0.2,0.4,0.4])

#前向算法
for i in range(len(O)):
    if i==0:
        pai=pai*B.T[O[i]]  #初始状态概率
    else:
        pai=pai.dot(A)*B.T[O[i]]   #之后的状态概率迭代
print(pai.sum())

3.后向算法

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
python代码实现–后向算法

Q=["box1","box2","box3"]#状态集合
V=["红","白"] #观测集合
#O=["红","白","红"]  #观测序列
O=[0,1,0] #转为数字类型
A=np.array([[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]])
B=np.array([[0.5,0.5],[0.4,0.6],[0.7,0.3]])
pai=np.array([0.2,0.4,0.4])

#后向算法
for i in range(len(O),0):
    if i==len(O):
        pai1=np.array([1,1,1])  #t=3时刻
    else:
        pai1=A.dot(B.T[O[i]]*pai1)##之前的状态概率迭代
print((pai1*pai*B.T[0]).sum())#终止

(二)模型参数学习

学习问题
在这里插入图片描述
没有找到具体例子，若用到，再更新…

(三)预测(解码)问题（例题+代码实现）

在这里插入图片描述

1.穷举

找出所有可能出现的情况，选择概率最大的一组

直接附代码

Q=["box1","box2","box3"]#状态集合
V=["红","白"] #观测集合
#O=["红","白","红"]  #观测序列
O=[0,1,0] #转为数字类型
A=np.array([[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]])
B=np.array([[0.5,0.5],[0.4,0.6],[0.7,0.3]])
pai=np.array([0.2,0.4,0.4])

#暴力破解 穷举
sum=0
pathlist=[]#存路径
plist=[]#存概率
for i in range(len(Q)):
    for j in range(len(Q)):
        for k in range(len(Q)):
            pathlist.append((i,j,k))
            plist.append(pai[i]*B[i][0]*A[i][j]*B[j][1]*A[j][k]*B[k][0])
            print((i,j,k),("%s*%s*%s*%s*%s*%s =")%(pai[i],B[i][0],A[i][j],B[j][1],A[j][k],B[k][0]),pai[i]*B[i][0]*A[i][j]*B[j][1]*A[j][k]*B[k][0])
#看概率最大的路径 则是最优

maxp=max(plist) #计算列表最大值                
xb=plist.index(maxp)#取出最大值所对应的下标
print("最优路径为：",pathlist[xb])#输出最优解pathlist[xb]
print("最优路径对应概率为：",plist[xb])#输出最大概率p[xb]

输出
在这里插入图片描述

2.维特比viterbi算法

维特比算法实际是用动态规划解隐马尔可夫模型预测问题，即用动态规划（dynamic programming）求概率最大路径（最优路径）．这时一条路径对应着一个状态序列．
定义两个变量：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
Python代码实现

Q=["box1","box2","box3"]#状态集合

V=["红","白"] #观测集合

#O=["红","白","红"]  #观测序列
O=[0,1,0] #转为数字类型


A=np.array([[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]])
B=np.array([[0.5,0.5],[0.4,0.6],[0.7,0.3]])
pai=np.array([0.2,0.4,0.4])

#维特比viterbi算法

maxxb=[] #存φ，b-->δ
for i in range(len(O)):
    if i==0:
        b=pai*B.T[0]#t=1时刻概率
    else:
        maxxb.append(np.argmax(b*A.T,axis=1)) #返回最大值下标,axis=1每行最大,axis=0每列最大
        b=np.max(b*A.T,axis=1)*B.T[O[i]]   #迭代取最大值

#print(list(maxxb))        
path=[]#最优路径

it=np.argmax(b,axis=0)#最优路径的“终点”
path.append(it)
for i in range(len(maxxb)):#最优路径回溯
    it=maxxb[len(maxxb)-i-1][it]
    path.append(it)

path.reverse()#把顺序调整一下，因为存的时候是倒着存储的   
print(path)

输出
[2, 2, 2]

![在这里插入图片描述](https://img-blog.csdnimg.cn/ec5ba9a65200419a84ccc1dfc1c78f04.png

公众号关注 52DATA ，获得更多数据分析知识,感谢支持—>

yanyanxiaobaobei
关注
  • 15
    点赞
  • 踩
  • 95
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 3
    评论
马尔可夫决策过程(MDP)原理与代码实战案例讲解
禅与计算机程序设计艺术
05-13 347
1. 背景介绍 1.1 马尔可夫决策过程的由来 马尔可夫决策过程(Markov Decision Process, MDP)是一种经典的序贯决策模型，其理论基础起源于20世纪50年代Richard Bellman提出的动态规划方法。MDP的核心思想是将复杂问题分解成一系列简单的决策步骤，并在每
6/6 随机过程 马尔科夫链 习题（随机过程应用与模型第三章）
ugly_g的博客
06-06 7370
2020.6.6 随机过程作业（如有错误欢迎大家指出） 例3.4 带一个吸收壁的简单随机徘徊 教材第3章 第1,8题 1.设马尔可夫链的转移矩阵为 8. 参考： 1.马尔可夫链习题课 2.矩阵的乘法 A的行×B的列 3.马尔可夫链PPT 4.特征值和特征向量 5.对角矩阵 ...
HMM隐马尔科夫模型例题讲解 加深印象
Mr番茄蛋的博客
10-31 4678
1.题目背景： 有一个小城，这里的天气只有晴天和阴天，有一个小女孩平时经常做的就是三件事：散步、购物、打扫。 她有一个在外地的男朋友，想知道她的城市里最近三天天气如何，但是女孩只告诉他，第一天她去购物，第二天打扫，第三天在散步。 现在男生用这现有的信息要推断出小女孩城市里这三天天气最可能的状态。 2.已知情况： 隐含的天气状态 = { 晴 , 阴 } 可观察的感觉状态 = { 购物
第十章 隐马尔可夫模型-习题
qq_40773666的博客
11-27 1714
10.1 本题考查概率计算的前向或后向算法: 前向算法：αt+1(i)=[∑j=1Nαt(j)∗aji]∗bi(Ot+1) \alpha_{t+1}(i) = [\sum_{j=1}^{N} \alpha_{t}(j)*aji]*b_{i}(O_{t+1})αt+1​(i)=[j=1∑N​αt​(j)∗aji]∗bi​(Ot+1​) 后向算法：βt(i)=∑j=1Naijbj(Ot+1)βt+1(j) \beta_t(i) = \sum_{j=1}^{N}a_{ij}b_{j}(O_{t+1})\beta
自然语言处理-HMM隐马尔可夫模型简介及例题介绍
最新发布
m0_69378371的博客
05-19 478
在隐马尔可夫模型（HMM）的前向算法中，我们通过递归计算前向概率来确定给定观察序列的概率。
隐马尔可夫模型(HMM) ｜前向算法 ｜一个简单的例子说清计算过程 ｜一般步骤总结
公众号：快乐变态屋 漂亮大男孩的罗德岛
03-15 1323
难者不会 会者不难 学习是有苦头的
马尔科夫系列——二、隐马尔可夫模型 - HMM的三个问题 - 概率计算问题
HUSTHY的博客
03-13 3062
转载自简书——隐马尔可夫模型 - HMM的三个问题 - 概率计算问题，把其中的有些公式排版做了简单修改!其中的后向概率算法有点难度！ 目录 一、HMM案例回顾 二、HMM典型的3个问题 1、概率计算问题 2、学习问题 3、预测问题 三、概率计算问题解决方案 1、暴力直接计算法 2、前向-后向算法 2.1 前向算法： 2.2HMM案例-前向算法 2.3 后向算法...
HMM隐马尔科夫模型及MATLAB实现
lbwnbdedede的博客
02-26 6749
隐马尔科夫模型 文章目录隐马尔科夫模型前言一、定义二、三个基本问题1、观测序列概率2、模型参数学习3、预测（解码）问题总结 前言 隐马尔科夫模型（HMM）是在马尔科夫链上的一个扩展，属于机器学习，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析 一、定义 隐状态集合：Q={q1,q2,…,qN} 可观测态集合：V={v1,v2,…,vN} 状态序列：I={i1,i2,…,iN} 观察态序列：O={o1,o2,…,oN} 状态转
隐马尔可夫模型（二）概率计算问题
weixin_43868020的博客
05-26 1976
概率计算问题 给定模型λ和观测序列O，计算在模型λ下观测序列O出现的慨率P（O|λ）。 具体问题描述 假设已知模型 λ ： 状态集合 S：健康，发烧； 可观测集合 O：正常、冷、头晕； 初始概率的状态矩阵 π： 转移矩阵 A： 观测状态转移概率矩阵（发射矩阵）B： 已知：观测序列 O ：正常，冷，头晕 问：在该模型 λ 下，观测序列 O出现的概率。 遍历法 在知道模型参数和观测序列的情况下，我们只需要列出所有可能的状态序列，然后求每个状态序列下的得到观察序列O的概率，再将这些概率相加起来就是我们最终
HMM隐马尔可夫模型最详细讲解与代码实现
m0_53292725的博客
07-01 2570
首先就要说到中文分词 现阶段的分词手法一般有三大流派1.基于规则： 前后向最大匹配2.基于统计:HMM, CRF3.基于深度学习：Bilstm+crf 那么我们今天重点要讲的就是其中之一HMM隐马尔可夫模型 再说一下为什么要进行分词？1.更好的理解语义（能够提高模型性能）2.为了更重要的任务 如(命名实体识别、情感分析、文本分类 、语义识别等等)3.应用场景的需要 （淘宝、百度）搜索算法对于分词的要求就非常高But 并非所有中文任务都需要进行分词！ 比如说 Bert （NSP）然后绕不开的一个点就是语料
机器学习之隐马尔科夫模型完整Python代码实现
weixin_40255359的博客
09-10 4100
encoding=utf8 import numpy as np import csv class HMM(object): def init(self,N,M): self.A = np.zeros((N,N)) # 状态转移概率矩阵 self.B = np.zeros((N,M)) # 观测概率矩阵 ...
第六章_马尔科夫预测法完整版
07-04
第六章_马尔科夫预测法完整版
ASR 隐马尔可夫模型（HMM）
01-07
隐马尔可夫模型（HMM） 简单理解HMM 数据科学中，预测是一个经久不衰的问题。以常见的时间为序数据为例，数据科学家期望对过去（t0t_{0}t0​时刻）和当前（tNt_{N}tN​时刻）数据的观察( Time )，实现预测未来（tN+...
HMM隐马尔可夫模型MATLAB实现
01-06
该资源直接运行runtest.m可测试HMM的评估和解码问题，运行baum_welch_test_mine.m测试HMM学习问题
10.2 基于隐马尔可夫模型（HMM）的孤立字语音识别_隐马尔可夫模型（HMM）的孤立字语音识别_
09-30
隐马尔可夫模型（HMM）的孤立字语音识别，matlab程序实现
Python基于隐马尔可夫模型拼音转中文算法实现源码+代码注释+数据.zip
08-09
Python基于隐马尔可夫模型-拼音转中文算法实现源码+代码注释+数据 【项目介绍】 该资源内项目代码都是经过测试运行成功，功能ok的情况下才上传的，请放心下载使用！ 本项目适合计算机相关专业(如计科、人工智能、...
HMM隐马尔可夫模型用于中文分词
05-11
HMM隐马尔可夫模型用于中文分词HMM隐马尔可夫模型用于中文分词
【机器学习】隐马尔可夫模型（HMM）
Make AI，Not War
06-11 2412
隐马尔可夫模型（HMM）1.部分参考内容2.引言3.隐马尔可夫模型的定义 1.部分参考内容 Youtube（无中文字幕） 隐马尔可夫模型(HMM)详解 2.引言 Alice和Bob住的很远，只能通过电话交流。 Bob的心情会随天气的好坏而变化，天气sunny的时候，他就happy，天气rainy的说话，他就grumpy。Bob通过电话告诉Alice他很happy，Alice就可以推测Bob那的天气是sunny，反之，也可以推测出rainy。 那么，如果问题再稍微复杂一点呢。 假如Bob的心情在s
隐马尔科夫模型练习
万德1010的博客
03-23 1554
import numpy DTYPE='float32' #学习问题 def forward(a,b,o): num_states_hidden=a.shape[0] alpha=numpy.ones((num_states_hidden,1),dtype=DTYPE) tem_alpha=numpy.zeros((num_states_hidden,1),dtype
隐马尔可夫模型（HMM）的MATLAB实现——Viterbi算法
05-05
HMM是一种常见的统计模型，用于描述随机生成的序列。Viterbi算法是一种在HMM中进行解码的动态规划算法，用于寻找最可能的隐藏状态序列。下面是HMM的MATLAB实现，包括Viterbi算法。 首先，我们需要定义一个HMM模型。我们假设这个模型有3个隐藏状态和2个可见状态。我们使用矩阵A表示隐藏状态之间的转移概率，矩阵B表示每个隐藏状态生成每个可见状态的概率，向量pi表示初始隐藏状态的概率分布。 ```matlab % 定义HMM模型参数 A = [0.5 0.2 0.3; 0.3 0.5 0.2; 0.2 0.3 0.5]; B = [0.5 0.5; 0.4 0.6; 0.7 0.3]; pi = [0.2 0.4 0.4]; ``` 接下来，我们需要生成一个可见序列。我们使用HMM模型中的随机过程生成一个长度为10的可见序列。 ```matlab % 生成可见序列 T = 10; q = zeros(1, T); o = zeros(1, T); q(1) = randsrc(1, 1, [1:3; pi]); o(1) = randsrc(1, 1, [1:2; B(q(1), :)]); for t = 2:T q(t) = randsrc(1, 1, [1:3; A(q(t-1), :)]); o(t) = randsrc(1, 1, [1:2; B(q(t), :)]); end ``` 接下来，我们使用Viterbi算法解码这个可见序列，得到最可能的隐藏状态序列。我们定义一个矩阵V表示每个时间步的最大概率，以及一个矩阵path表示每个时间步的最大概率对应的前一个状态。 ```matlab % Viterbi算法解码 V = zeros(3, T); path = zeros(3, T); V(:, 1) = pi' .* B(:, o(1)); for t = 2:T for j = 1:3 [V(j, t), path(j, t)] = max(V(:, t-1) .* A(:, j)); V(j, t) = V(j, t) * B(j, o(t)); end end ``` 最后，我们找到最可能的隐藏状态序列。我们首先找到最后一个时间步的最大概率对应的隐藏状态，然后从后往前依次寻找每个时间步的最大概率对应的隐藏状态，最终得到整个隐藏状态序列。 ```matlab % 找到最可能的隐藏状态序列 [~, q(T)] = max(V(:, T)); for t = T-1:-1:1 q(t) = path(q(t+1), t+1); end ``` 完整代码如下： ```matlab % 定义HMM模型参数 A = [0.5 0.2 0.3; 0.3 0.5 0.2; 0.2 0.3 0.5]; B = [0.5 0.5; 0.4 0.6; 0.7 0.3]; pi = [0.2 0.4 0.4]; % 生成可见序列 T = 10; q = zeros(1, T); o = zeros(1, T); q(1) = randsrc(1, 1, [1:3; pi]); o(1) = randsrc(1, 1, [1:2; B(q(1), :)]); for t = 2:T q(t) = randsrc(1, 1, [1:3; A(q(t-1), :)]); o(t) = randsrc(1, 1, [1:2; B(q(t), :)]); end % Viterbi算法解码 V = zeros(3, T); path = zeros(3, T); V(:, 1) = pi' .* B(:, o(1)); for t = 2:T for j = 1:3 [V(j, t), path(j, t)] = max(V(:, t-1) .* A(:, j)); V(j, t) = V(j, t) * B(j, o(t)); end end % 找到最可能的隐藏状态序列 [~, q(T)] = max(V(:, T)); for t = T-1:-1:1 q(t) = path(q(t+1), t+1); end ```

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 3
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

yanyanxiaobaobei

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值