参考 :ZOE’s MindMap、 统计学(贾俊平版)
阅读提示:内容较长为了检索便捷;如有错误,请指出。
笔记提示:部分内容暂时未完善,后续不断更新
数学基础扫盲
认识
数学是一个工具:通过收集、分析、解读数字中的信息
- 面试
对概率论和数理统计的基础知识的考察是重要组成部分。因为在工作中很多分析报告和制定策略都是基于概率统计和数据统计的一些定理。
在面试和实际工作中更加着重对于,结合工作这些知识点的理解和应用
1. 描述性统计
1.基本概念
- 数据分类 1
| 数据 | 类型 | 逻辑与数学运算 | 举例 |
|---|---|---|---|
| 定性数据 | 定类尺度 | = != | 身份证 |
| 定序尺度,次序 | = != < > | 年级 | |
| 定量数据 | 定距尺度,上述属性+有固定单位 | = != < >+ - | 分数、温度 |
| 定比尺度,上述属性+比例意义 | = != <>+ -*/ | 长度、高度、利润、薪酬、产值 |
-
截面数据与时序数据
- 截面数据:也称静态数据指在同一时间截面上反映一个总体的一批,如:人口普查数据
- 时间序列数据:同一统一指标按时间顺序记录的数据列,例如:某省从1940年至1999年各个年末的人口数是由50个时点数组成的时序数列
-
描述统计
用数值、表格、图形等汇总数据,使得数据易于理解和解释。 -
推断统计
用样本数据对总体数据进行估计和假设检验 -
数据展示&目的
- 数据分布
条形图 :频数/相对频数分布
饼形图 :相对频数/百分比频数分布 - 数据数值
打点图 :整个数据范围内的分布
直方图 :在一个「区间组集合」上的「频数分布
茎叶显示 :展示等级顺序和分布形态 - 进行比较
复合条形图
结构条形图 - 相关关系
散点图
趋势图
- 数据分布
2.表格图形
1.单变量
- 分布型数据
- 表格方法
- 频数分布,数据的表格汇总
- 相对频数分布,算公式为:频数/总数=相对频数。
- 图形方法
- 条形图 bar chat
横轴:组别;纵轴:频数/相对频数 - 饼图 pie chat
相对频数
- 条形图 bar chat
- 表格方法
- 数值型数据
- 表格方法
- 频数分布
步骤:1.确定组数(互不重叠) 2.确定每组的宽度,近似组宽=(max-min)/组数 3. 确定组限,确保每个数据落在一个组内 - 相对频数分布
- 累计分布
表格汇总
图形化:累计曲线 ogive
- 图形方法
- 打点图 dot plot
模轴表示数据值域,每一数据值用打在数轴上的点表示。如值=18的点有三个,就在18的位置打三个点; - 直方图 histogram
纵轴:频数/相对频数。与 bar plot 的区别 ,矩形相连,反映数据的形态分布 - 茎叶图
- 打点图 dot plot
2.双变量
- 表格方法
- 交叉分组表
同时展示两个变量的表格。注意辛普森悖论,单独的表与交叉表得出不同的结论。原因是,存在影响结论的隐藏变量,注意需要斟酌个别分组的权重,以一定的系数去消除以分组资料基数差异所造成的影响,同时必需了解该情境是否存在其他潜在要因而综合考虑。
- 交叉分组表
- 图形方法
- 数值数据
散点图:数量变量间的关系
趋势图:相关性近似程度表达 - 分类数据
复合/簇状条形图 side by side
结构/堆砌条形图 stacked chart
- 数值数据
2.数值方法
概述 :度量样本和总体参数
包括:
- 中心位置
- 平均值
- 众数
- 中位数
- 分位数
- 变异程度
- 四分位数间距
- 方差&标准差
- 标准差系数
- 平均值绝对偏差
- 分布形态
- 偏度
- 峰度
- Ȥ分数
- 相对位置
- 切比雪夫定理
- 经验法则
- 异常值
- 线性关系
- 协方差
- 相关性系数
1.中心位置的度量
数据集中趋势的度量
- 平均值
用来表示随机变量的理想平均水平。随着实验次数的增多,x的均值会越发趋近于期望值。- 公式
- 离散型随机变量。基于分布率。Ex:随机变量及其对应的概率两者的乘积的累加。
E ( X ) = ∑ k = 1 ∞ x k p k E(X)=\displaystyle\sum^\infty_{k=1}x_kp_k E(X)=k=1∑∞xkpk - 连续型随机变量,基于概率密度函数fx。
E ( X ) = ∫ − ∞ ∞ x d x E(X)=\displaystyle\int^{\infty}_{-\infty}{xdx} E(X)=∫−∞∞xdx
- 离散型随机变量。基于分布率。Ex:随机变量及其对应的概率两者的乘积的累加。
- 类别
- 算术平均数,调整平均数:P%平均数,删除P%的最大值和最小值后的均值
x ‾ = ∑ i = 1 ∞ x i n \overline x=\frac{\displaystyle\sum^\infty_{i=1}x_i}{n} x=ni=1∑∞xi - 加权平均数
x ‾ = ∑ i = 1 k x i f i ∑ i = 1 k f i \overline x=\frac{\displaystyle\sum^k_{i=1}x_if_i}{\displaystyle\sum^k_{i=1}f_i} x=i=1∑kfii=1∑kxifi - 几何平均数
n个数值乘积的n次方,应用:确定几个连续时期的平均变化率,例如财务的 增长率
G n = x 1 x 2 x 3 … … x n n G_n=\sqrt[n]{x_1x_2x_3……x_n} Gn=nx1x2x3……xn
- 公式
- 众数 mode
出现次数最多的数, 不受极端值得影响。众数只有在数据 量较大的时候才 有意义。且众数可能有多个,但多个众数无意义 - 中位数 median
包含异常值时,比均值更合适 - 分位数
随机变量在样本中的排序情况,是指将一个随机变量的概率分布范围分为几个等份的数值点,常用的有中位数(即二分位数)、四分位数、百分位数等。作用 :用来监测异常数据:根据业务规则设定一个合理的分位区间,区间之外的数据要进行异常处理。例如和历史订单量相比,单日订单量过高过低都要进行相应的分析 - 公式
求对应分位数对应的值
X p = X L + p ∗ N − F L F p i p X_p=X_L+\frac{p*N-F_L}{F_p}i_p Xp=XL+Fpp∗N−FLip
p 百分位数,位置指标 、L 位置前一个分组上限 、N 样本总数或频数、Fl前一个分组频数 、Fp P 所在位置分组频数 、ip 分组的长度- 百分位数
- 定义 :第p百分位数 至少有p%的观测值<=该值 且 至少有(1-p%)的观测值>=该值
- 计算
- 数据按「升序」排列
- i= (P/100)n
p为百分位数 n为观测值个数 ;i 不是整数 向上取整(大于i的下一个整数)\i是整数 第ⅰ和(i+1)项的平均值
- 常用
四分位数 第25、50、75百分位数 50百分位数○=○中位数
五分位数 第20、40、60、80百分位数
十分位数⊙第10、20…90百分位数
第
- 四分位数
Q1: P=25%, 较小四分位数
Q2: P=50%, 中位数
Q3: P=75%, 较大四分位数
- 百分位数
2.变异程度的度量
数据的离散程度
- 极差range
d = max -min,用于粗略检查产品 质量 的稳定性和进行质 量控制 - 四分位数间距IQR
IQR = Q3- Q1 ,中间50%数据的极差 - 方差 D(X)
样本与均值的离差平方和的均值 ,度量随机变量偏离期望的程度,刻画数据的波 动性和稳定性,方差越大,结果未知性越大。
总体方差: σ 2 = ∑ ( x i − μ ) 2 N \sigma^2=\frac{\sum{(x_i-\mu)^2}}{N} σ2=N∑(xi−μ)2
样本方差: s 2 = ∑ ( x i − x ‾ ) 2 n − 1 s^2=\frac{\sum{(x_i-\overline x)^2}}{n-1} s2=n−1∑(xi−x)2
样本方差估计总体方差:1.无偏差估计:采用(n-1)总体方差总是比样本方差大一点, - 标准差 𝜎(X)
s = s 2 s=\sqrt {s^2} s=s2
σ = σ 2 \sigma=\sqrt {\sigma^2} σ=σ2
标准差也被称为标准偏差,或者实验标准差,与原数值单位相同,易于解释更常用,在概率统计中最常使用作为统计分布程度上的测量依据 - 标准差系数
(标准差/平均值)*100% ,用于对变异程度的相对度量,比较不同标准差和不同均值的变异程度 - 平均值绝对偏差MAE
M A E = ∑ ∣ x i − x ‾ ∣ n MAE=\frac{\sum|x_i-\overline x|}{n} MAE=n∑∣xi−x∣
用于时间序列
3.分布形态的度量
偏度 峰度
- 正态分布
详情位于4.3 - 偏度 Skewness
数据的偏袒方向和程度- 偏态系数SK
S K = n ( n − 1 ) ( n − 2 ) ∑ ( x i − x ‾ s d ) 3 SK=\frac{n}{(n-1)(n-2)}\sum(\frac{x_i-\overline x}{sd})^3 SK=(n−1)(n−2)n∑(sdxi−x)3
n 表示样本总数 ,xi 表示样本数据 ,X- 表示样本 平均值 表示样本标准差 - 偏斜方向
分布的期望和中位数大小的关系
数据的偏态,近似:波峰位置可能是中位数和众数,均值是面积的一半 - 无偏态分布,SK = 0
基本特性:平均数=中位数=众数。概率密度函数的图形以期望为中心,左右对称,中间为最高值两边低 绝大多数样本都会落在期望值附近,也就3𝜎 - 右向偏态/正向偏态,SK >0
基本特性:平均值>众数 平均数>中位数 ,均值、极端值在右,曲线 向右延伸。
- 偏态系数SK
- 左向偏态/负向偏态 SK <0
基本特征:平均值<众数 平均值<中位数 ,均值、极 端值在左,曲线 向左延伸

- 峰度 Kurtosis
峰度系数K,用来反映频数分布曲线的陡缓程度:顶端尖峭或扁平程度的指标。K越大,陡缓程度与正态分布的差异性越大。

- 峰度系数值
在正态分布情况下,峰度系数值是3(但是SPSS等软件中将正态分布峰度值定为0,是因为已经减去3,这样比较起来方便)。>3的峰度系数说明观察量更集中,有比正态分布更短的尾部;<3的峰度系数说明观测量不那么集中,有比正态分布更长的尾部,类似于矩形的均匀分布。 - 标准误
峰度系数的标准误用来判断分布的正态性。峰度系数与其标准误的比值用来检验正态性。如果该比值绝对值大于2,将拒绝正态性。
- 峰度系数值
- 标准峰度 k=0
相对正态分布曲线的标准峰度
- 平顶峰度 k<0
数据在众数周围分布较分散 扁平、瘦尾、肩部较胖

- 尖顶峰度 K > 0
数据在众数周围分布较集中尖峰,肥尾、肩部较瘦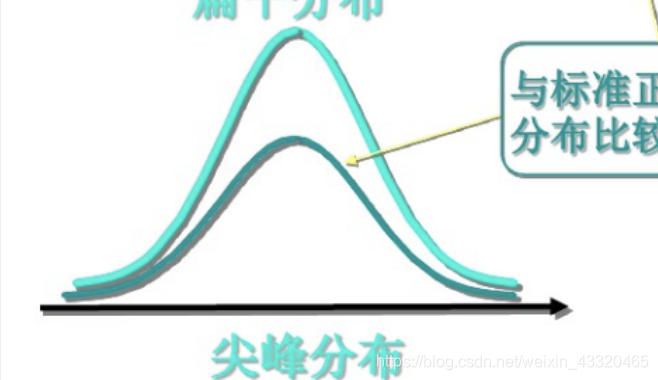
4.相对位置的度量(归一化)
本质上是为了消除指标之间的量纲影响方便比较:
不同评价指标往往具有不同的量纲和量纲单位,为了消除指标之间的量纲影响,需要进行数据标准化处理,原始数据经过数据标准化处理后,各指标处于同一数量级,适合进行综合对比评价
z-score
- z-score 标准分数
标准分数、 也叫z分数,是一种具有相等单位的量数零-均值规范化也称标准差标准化,经过处理的数据的均值为0,标准差为1 ,归一化在-1–+1之间。标准差分数可以回答这样一个问题:"给定数据距离其均值多少个标准差"的问题,在均值之上的数据会得到一个正的标准化分数,反之会得到一个负的标准化分数。
转化公式为: x ∗ = x − x ‾ σ x^*=\frac{x-\overline x}{\sigma} x∗=σx−x σ \sigma σ为原始数据的标准差,是当前用得最多的数据标准化方式。 - 异常值检测
基于IQR,大于上限或者小于下限。Lower Limit = Q 1 Q_1 Q1-1.5( IQR),Upper Limit = Q 3 Q_3 Q3 +1.5 ( IQR) - 衍生1:正态分布
(详情位于4.3“经验法则”)
无量纲化处理
- z-score 还有
- 相对标准化
这种方法是先给一个评价指标确定一个标准值,然后用实际值和标准值进行比较,实现指标的相对化处理,公式为:
z i = x i x s z_i=\frac{x_i}{x_s} zi=xsxi
x i x_i xi为进行标准化确定的对比标准,通常可以选择最优值或平均值作为对比标准。定的标准不同,标准值的含义也就不同。这种方法可以体现评价者进行评价的目标性。 - min-max标准化(Min-Max Normalization)
对多目标规划原理中的功效系数加以改进,从而把要评价的指标转化为可以度量的评判分数,公式为:
z i = x i − m i n ( x i ) m a x ( x i ) − m i n ( x i ) z_i=\frac{x_i-min(x_i)}{max(x_i)-min(x_i)} zi=max(xi)−min(xi)xi−min(xi)
按该方法计算, z i z_i zi的取值在0~1之间。- 拓展:
标准化分数在60~100之间
本章开头的统计应用专栏中,中国人民大学中国发展指数(RCDI)就是按功效系数法对各指标值进行标准化处理的将功效系数法进行一些拓展,会得到改进的功效系数法,公式为
z i = x i − m i n ( x i ) m a x ( x i ) − m i n ( x i ) ∗ 40 + 60 z_i=\frac{x_i-min(x_i)}{max(x_i)-min(x_i)}*40+60 zi=max(xi)−min(xi)xi−min(xi)∗40+60
这样得到的。这种处理的效果在于,可以减小极端数值对计算结果的视觉影响,接近人们对分数的一般看法。
- 拓展:
- 区间值归一化
如果是区间上的值,则可以用区间上的相对位置来归一化,即选中一个相位参考点,用相对位置和整个区间的比值或是整个区间的给定值作比值,得到一个归一化的数据,比如类似于一个概率值0<=p<=1; - 其他归一法
比如对数归一,指数归一,三角or反三角函数归一等
大数定理
- 衍生2:大数定理
-
核心
偶然中包含着某种必然。在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率(均值接近于期望)。不是经验规律,而是在一些附加条件上经严格证明了的定理,表达一种自然规律因而通常不叫定理而是大数“定律”。大数定律有若干个表现形式。这里仅介绍高等数学概率论要求的常用的三个重要定律: -
切比雪夫大数定理
公式一,任意一个数据集中,距离其平均数 z个标准差范围内的比例(或部分)总是至少为1-1/z^2,其中z为大于1的任意正数。常数:z=2,z=3和z=5有如下结果:
所有数据中,至少有3/4(或75%)的数据位于平均数2个标准差范围内。
所有数据中,至少有8/9(或88.9%)的数据位于平均数3个标准差范围内。
所有数据中,至少有24/25(或96%)的数据位于平均数5个标准差范围内
注意:切比雪夫大数定理为依据样本平均数估计总体平均数提供了理论依据,适用于任何数据集,无论数据的分布,随着样本容量n的增加,样本平均数将接近于总体平均数。并未要求同分布,相较于后面介绍的伯努利大数定律和辛钦大数定律更具一般性 ,更强的适用性。 -
伯努利大数定律
设μ是n次独立试验中事件A发生的次数,且事件A在每次试验中发生的概率为P,则对任意正数ε,有公式二,该定律是切比雪夫大数定律的特例,其含义是,当n足够大时,事件A出现的频率将几乎接近于其发生的概率,即频率的稳定性。在抽样调查中,用样本成数去估计总体成数,其理论依据即在于此 [1] 。 -
辛钦大数定律
常用的大数定律,设 {ai,i>0}为独立同分布的随机变量序列,若ai 的数学期望存在,则服从大数定律,即对任意的ε>0,有公式三 [1] ,
-
| 公式 | 分布情况 | 期望 | 方差 | 总结 | |
|---|---|---|---|---|---|
| 公式一: | 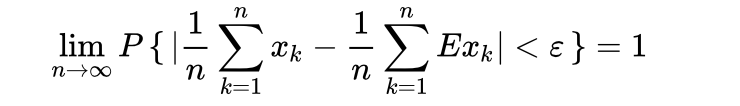 | 相互独立或者不相关 | 存在 | 存在 | 估算期望 |
| 公式二: | 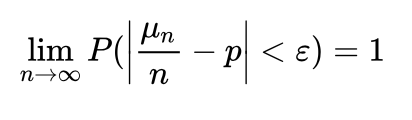 | 二项分布 | 相同 | 相同 | 频率等于概率 |
| 公式三: | 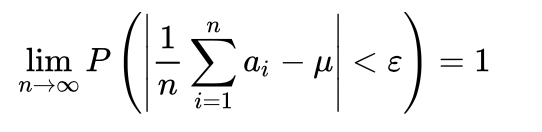 | 相互独立且同分布 | 相同 | 相同 | 估算期望 |
5.两变量线性关系的度量
- 关系
- 联合分布
F(X,Y)=Pr(X≤x,Y≤y)
在概率论中, 对两个随机变量X和Y,其联合分布是同时对于X和Y的概率分布。分布函数F(X,Y)在(x,y)处的函数值,是随机变量落在,以点(x,y)为顶点,该点左下方无穷矩形域内的概率。 - 独立分布
F(X,Y) = F(X)*F(Y)
及边缘分布函数,简化为:满足公式的分布
p(A|B)=p(A) p(B|A)=p(B) p(AB)=p(A)(B) - 相关性和 和独立性的区别,
独立性是不相关性的充分不必要条件,“不相关”是一个比“独立”要弱的概念,范围更大,指非线性关系。x-y不是线性关系,但存在可能x^2 - y 是线性关系,x-y 不相关但是也不独立。而只要独立,一定不相关。
- 联合分布
协方差
-
协方差 Cov(X,Y)
协方差表示的是两个变量的总体的误差的期望。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。 期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为:- 公式
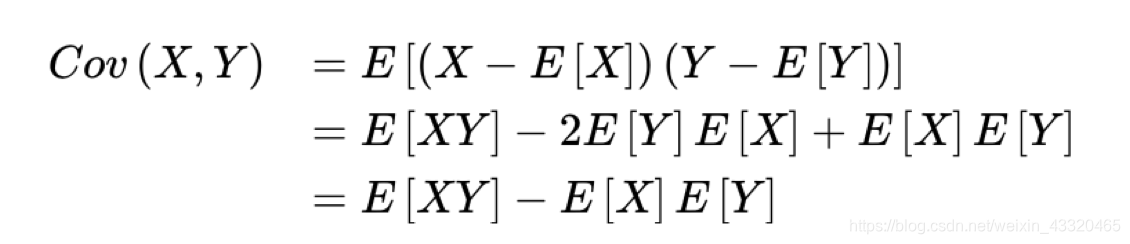
- 公式
| 公式 | 表达式 | |
|---|---|---|
| 样本协方差 | S x y = ∑ ( x i − x ‾ ) ( ( y i − y ‾ ) n − 1 S_x{_y} =\frac{\sum(x_i-\overline x)((y_i-\overline y)}{n-1} Sxy=n−1∑(xi−x)((yi−y) | 样本n |
| 总体协方差 | S x y = ∑ ( x i − μ x ) ( ( y i − μ y ) N S_x{_y} =\frac{\sum(x_i- \mu_x)((y_i-\mu_y)}{N} Sxy=N∑(xi−μx)((yi−μy) | 总样本 |
-
解释
正值 正相关 负值 负相关 零 无相关性 - 缺点(补救方式,采用相关系数。)
- 采用不同计量单位,结果差异明显
- 用数值衡量线性关系强度有偏差。
- 缺点(补救方式,采用相关系数。)
相关系数
-
相关系数
又称为皮尔逊积矩相关系数。相关系数定量地刻画了 X 和 Y的相关关系,而非因果,范围(-1,1),关系越弱越接近0- 公式
| 公式 | 表达式 | |
|---|---|---|
| 样本相关系数 | r x y = s x y s x s y r_x{_y} =\frac{s_x{_y}}{s_xs_y} rxy=sxsysxy | 样本相关系数是对总体相关系数的点估计。 |
| 总体相关系数。 | ρ x y = σ x y σ x s y \rho_x{_y} =\frac{\sigma_x{_y}}{\sigma_xs_y} ρxy=σxsyσxy | 将样本统计量全部替换为总体参数即可。 |
( s x y s_x{_y} sxy为X与Y的协方差 、 s x s_x sx为X的方差、 s y s_y sy为Y的方差)
- 复相关系数
又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如,某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。 - 典型相关系数
是先对原来各组变量进行主成分分析,得到新的线性关系的综合指标,再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。
6.探索性数据分析
箱型图
- 箱型图
- 基于“五数”
最小值、第一四分位数(Q1)、中位数(Q2)、第三四分位数(Q3)、最大值 - 步骤
- Q1,Q2,Q3
- 触须线 延伸至最大最小值
确定上下限:Lower Limit = Q 1 Q_1 Q1-1.5( IQR),Upper Limit = Q 3 Q_3 Q3 +1.5 ( IQR) - 异常值
上下限之外的值
- 基于“五数”
3.概率
1.概率基础
- 基本概念
- 随机现象
偶然性、并不总是出现相同结果。投掷一颗骰子出现的次数 - 随机事件
随机现象的某些基本结果组成的集合。{1,2,3,4,5,6}
随机事件在一次试验中发生与否是不确定的多次试验时含有规律性 - 试验
在相同条件下进行大量的重复试验- 具有三个特征: 1.单个结果无法确定,全部的结果可以确定 2.过程可重复
- 概率
用数据度量某件事发生的可能性的大小, P ( A ) = n A N P(A)=\frac{n_A}{N} P(A)=NnA, n A n_A nA:A发生的次数,N:实验次数 - 样本空间
所有可能结果组成的一个集合。 - 样本点
任何一个特定的实验结果或者样本空间的一个元素。
- 随机现象
排列组合
- 计数法则
-
多步骤试验
- 计数法则:1.如果一个实验可以分成循环的k步骤2.第i步有ni实验结果3.那么所有可能的实验结果总称为 ( n 1 n_1 n1)( n 2 n_2 n2)( n 3 n_3 n3)(……)( n k n_k nk)
- 图形分析:树形图
-
组合
-
定义
从n项中不计次序取出m(m≤n,m与n均为自然数,下同)并成一组,叫做一个组合;所有组合的个数,叫组合数。用符号 C n m C_n^m Cnm表示。 -
计算公式
C n m = A n m m ! = n ! m ! ( n − m ) C_n^m=\frac{A^m_n}{m!}=\frac{n!}{m!(n-m)} Cnm=m!Anm=m!(n−m)n!
C ( n , m ) = C ( n , n − m ) C(n,m)=C(n,n-m) C(n,m)=C(n,n−m)
-
-
排列
- 定义
从n个不同元素中,任取m个按照一定的顺序排成一列,叫一个排列;所有排列的个数,叫排列数,符号 A n m A_n^m Anm - 计算公式

- 定义
-
概率分配
- 两个基本条件
0 ≤ P ( E i ) ≤ 1 0 \leq P(E_i)\leq1 0≤P(Ei)≤1 for all i
P ( E 1 ) + P ( E 2 ) + … + P ( E n ) = 1 P(E_1)+P(E_2)+\ldots+P(E_n)=1 P(E1)+P(E2)+…+P(En)=1
- 两个基本条件
-
常用方法
- 古典法 :所有试验结果发生的可能性相等 1/N
- 相对频数法:试验可以「大量重复」进行,能取得试验结果「发生比率」的数据
- 主观法
不符合上述两种方法的使用条件时使用,以主观判断为基础范围0-1之间。
计算:贝叶斯定理,结合「主观」确定的「先验概率」和「其他方法」得到的概率
-
2.事件及其概率
- 事件
样本点的一个集合。特例;样本空间是一个事件 - 事件的概率
事件中所有样本点的概率之和 - 概率的基本性质
- 补事件: P ( A ) = 1 − P ( A c ) P(A)=1-P(A^c) P(A)=1−P(Ac)
- 并事件:属于a或b或者同时属于
- 交事件:同时授予AB
- 加法公式
- 计算并事件的概率
- P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) ) P(A\cup B)=P(A)+P(B)-P(A\cap B)) P(A∪B)=P(A)+P(B)−P(A∩B))
- 独立事件 P ( A ∪ B ) = P ( A ) + P ( B ) ) P(A\cup B)=P(A)+P(B)) P(A∪B)=P(A)+P(B))
- 条件概率
- 在B发生的条件下A发生的概率。
- P ( A ∣ B ) = P ( A ∩ B ) P ( B ) P(A|B)=\frac{P(A\cap B)}{P(B)} P(A∣B)=P(B)P(A∩B)
- 联合概率和边际概率的比值
- 联合概率:两个事件都发生的概率
- 边际概率,每个事件各自发生的概率
- 乘法公式
P ( A ∩ B ) = P ( A ) P ( A ∣ B ) P(A\cap B)=P(A)P(A|B) P(A∩B)=P(A)P(A∣B)/ P ( A ∩ B ) = P ( B ) P ( B ∣ A ) P(A\cap B)=P(B)P(B|A) P(A∩B)=P(B)P(B∣A)- 独立事件: P ( A ∩ B ) = P ( A ) P ( B ) P(A\cap B)=P(A)P(B) P(A∩B)=P(A)P(B)
- 独立事件:P(A|B) = P(A) P(B|A)=P(B)
3.贝叶斯定理
-
定义
事件A在事件B(发生ki)的条件下的概率,与事件B在事件A的条件下的概率,这两者之间的关系.公式表示:在 B 发生的条件下 A 发生的条件概率,等于 A 事件发生条件下B 事件发生的条件概率乘以 A 事件的概率,再除以 B 事件发生的概率。- 已知:
- 每个 A事件的概率: P ( A 1 ) , P ( A 2 ) , P ( A 3 ) , P ( A 4 ) , … P(A_1),P(A_2),P(A_3),P(A_4),\ldots P(A1),P(A2),P(A3),P(A4),…
- 对应B发生的概率: P ( B ∣ A 1 ) , P ( B ∣ A 2 ) , P ( B ∣ A 3 ) , P ( B ∣ A 4 ) , … P(B|A_1),P(B|A_2),P(B|A_3),P(B|A_4),\ldots P(B∣A1),P(B∣A2),P(B∣A3),P(B∣A4),…
- 求:
- A事件的条件概率: P ( A 1 ∣ B ) 或 P ( A 2 ∣ B ) 或 P ( A 3 ∣ B ) … P(A_1|B)或P(A_2|B)或P(A_3|B)\ldots P(A1∣B)或P(A2∣B)或P(A3∣B)…
- 已知:
-
贝叶斯统计思想。
先 验 概 率 P ( A ) → 新 信 息 → 贝 叶 斯 定 理 → 后 验 概 率 P ( A ∣ B ) 先验概率P(A)\rightarrow新信息\rightarrow贝叶斯定理\rightarrow 后验概率 P(A|B) 先验概率P(A)→新信息→贝叶斯定理→后验概率P(A∣B) 修正决策思维:利用搜集到的信息对原有判断进行修正提供了有效手段:当你不能准确知悉一个事物的本质时,你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。- 先验概率P(A) :决策者通过经验来判断事情发生的概率,比如南方的梅雨季是 6-7 月,就是通过往年的气候总结出来的经验,这个时候下雨的概率就比其他时间高出很多。
- 后验概率P(A|B) :根据样本信息计算,条件概率的一种:发生结果之后,推测原因的概率比如说某人查出来了患有“贝叶死”,那么患病的原因可能是 A、B 或 C。患有“贝叶死”是因为原因 A 的概率就是后验概率。
- 似然函数(likelihood function):概率模型的训练过程理解为求参数估计的过程。似然函数就是用来衡量这个模型的参数。似然在这里就是可能性的意思,它是关于统计参数的函数 如果一个硬币在 10 次抛落中正面均朝上。那么你肯定在想,这个硬币是均匀的可能性是多少?这里硬币均匀就是个参数。
-
公式
P ( A i ∣ B ) = P ( B ∣ A j ) P ( A j ) ∑ j P ( B ∣ A j ) P ( A j ) P(A_i|B)=\frac{P(B|A_j)P(A_j)}{\sum _jP(B|A_j)P(A_j)} P(Ai∣B)=∑jP(B∣Aj)P(Aj)P(B∣Aj)P(Aj)
后验概率 = (似然度 * 先验概率)/标准化常量
也就是说,后验概率与先验概率和似然度的乘积成正比另外,比例 P ( B ∣ A ) P ( B ) \frac{P(B|A)}{P(B)} P(B)P(B∣A)也有时被称作标准似然度(standardised likelihood),Bayes法则可表述为:后验概率 = 标准似然度 * 先验概率。- P(A|B) 后验概率
B的前提下A的条件概率 - P(A) 先验概率
A的先验概率或边缘概率。 - P(B)
B的先验概率或边缘概率,也作标准化常量(normalized constant)。
- P(A|B) 后验概率
-
推理
P(A|B)=P(AB)/P(B)
P(AB)=P(A)P(B|A)=P(B)P(A|B)
P(A|B)=P(B|A)*P(A)/P(B)
假设A服从离散分布事件a所有的可能记A1,A2。
P(A1|B)+P(A2|B)……=1
两边同时乘以P(B)
P(B)=P(A1|B)P(B)+P(A2|B)P(B)……
P(B)=P(B|A1)P(A1)+P(B|A2)P(A2)……
转换为贝叶斯公式
P(A|B)=P(AB)/P(B)=P(B|A)*P(A)/P(B)
P ( A i ∣ B ) = P ( B ∣ A j ) P ( A j ) ∑ j P ( B ∣ A j ) P ( A j ) P(A_i|B)=\frac{P(B|A_j)P(A_j)}{\sum _jP(B|A_j)P(A_j)} P(Ai∣B)=∑jP(B∣Aj)P(Aj)P(B∣Aj)P(Aj) -
案例1.
一座别墅在过去的 20 年里一共发生过 2 次被盗,别墅的主人有一条狗,狗平均每周晚上叫 3 次,在盗贼入侵时狗叫的概率被估计为 0.9,问题是:在狗叫的时候发生入侵的概率是多少?
我们假设 A 事件为狗在晚上叫,B 为盗贼入侵,则以天为单位统计,
P(A) = 3/7
P(B) = 2/(20*365) = 2/7300
P(A|B) = 0.9
P(B|A) =P(AB)/P(A)=P(A|B)P(B)/P(A)= 0.9(2/7300) / (3/7) = 0.00058 -
案例2. 三门问题
思路:简化为在已知一只羊的情况下,选中车的概率 -
案例 3
假设有一种病叫做“贝叶死”,它的发病率是万分之一,即 10000 人中会有 1 个人得病。现有一种测试可以检验一个人是否得病的准确率是 99.9%,它的误报率是 0.1%,那么现在的问题是,如果一个人被查出来患有“叶贝死”,实际上患有的可能性有多大?
我们假设:A 表示事件 “测出为阳性”, 用 B1 表示“患有贝叶死”, B2 表示“没有患贝叶死”。根据上面那道题,我们可以得到下面的信息。患有贝叶死的情况下,测出为阳性的概率为 P(A|B1)=99.9%,没有患贝叶死,但测出为阳性的概率为 P(A|B2)=0.1%。另外患有贝叶死的概率为 P(B1)=0.01%,没有患贝叶死的概率 P(B2)=99.99%。
1.求标准化常量的各个部分 。
我们检测出来为阳性,而且是贝叶死的概率 P(B1,A)=P(B1)*P(A|B1)=0.01%*99.9%=0.00999%= 0.01%
这里 P(B1,A) 代表的是联合概率,同样我们可以求得检测出来为阳性,没有患贝叶死P(B2,A)=P(B2)*P(A|B2)=99.99%0.1%=0.09999%= 0.1%
2.带入公示
然后我们想求得是检查为阳性的情况下,患有贝叶死的概率,也即是 P(B1|A)。所以检查出阳性,且患有贝叶死的概率为:
P(B1|A)= P(A|B1) P(B1)/(P(B1)*P(A|B1)+P(B2)*P(A|B2))=0.01%/( 0.1%+0.01%)=9%
3.总结- 难点是能将问题转化为贝叶斯公式,如果不能理解,就按照公式展开求各个部分
- P(B1)、P(B2) 先验概率.知道了被检测出来是阳性,来求患贝叶死的概率,也就是求后验概率。
- 0.01%+0.1% 均出现在了 P(B1|A) 和 P(B2|A) 的计算中作为分母。我们把它称之为论据因子,也相当于一个权值因子。
4概率分布
1.基础
- 随机变量
依据:是否可数
区别于是有限。可数的含义是,随机变量是否能按照一定的次序列举。网站访问的用户数可以是无限,但依旧可以列举,为离散型随机变量。用户的转换率在0~1之间,但无法依次列举。
| 类型 | 定义 | 表达 |
|---|---|---|
| 连续型随机变量 | 实验结果落在某个区间的概率,随机变量X小于等于x的概率,也称为累计分布函数(CDF) | F(x)=Pr(X≤x) |
| 离散型随机变量 | 实验结果为具体某值的概率 | Pr(X=x) |
- 概率分布
- 定义
描述随机变量不同取值的概率。 - 内涵
由概率函数或者概率密度函数来定义概率分布。 - 分类
- 离散概率分布
- 表达形式
概率函数、表格形式 - 概率分配
古典法、主观法、相对频率法 - 概率函数
离散型均匀分配: f(x)= 1/n
- 表达形式
- 连续概率分布
- 概率密度函数 :概率为在给定区间曲线f(x)下的面积,只讨论区间值。曲线f(x)面积=1
- 常见
正态分布、指数分布、幂律分布、均匀分布
- 离散概率分布
- 定义
- 基本特征
期望、方差
2.离散概率分布
- 基本特征
- 期望
E ( x ) = μ = ∑ x f ( x ) E(x)= \mu=\sum xf(x) E(x)=μ=∑xf(x) - 方差
V a r ( X ) = σ 2 = ∑ ( x − μ ) 2 f ( x ) Var(X)= \sigma^2=\sum(x-\mu)^2f(x) Var(X)=σ2=∑(x−μ)2f(x)
- 期望
伯努利分布
- 伯努利分布
也称01分部。每次试验,结果非1及0,1的概率为p。无随机变量,分布律:P(X =1)=p ,p(X=0)= 1-p;期望:p ;方差:p(1-p)。例如:优惠券是否使用,P(X=1)=p则为转化率
二项分布
- 二项分布
- 定义:N个独立重复的伯努利分布。n个概率为p的独立可重复试验,随机变量x表示n次试验中成功的次数。发放1000张优惠券,是否被使用可以看作n=1000,概率为P独立重复实验。从而得到有 K张优惠券被使的概率P
- 公式
P P P { X = k X=k X=k}= ( k n ) P k ( 1 − p ) n − k (^n_k)P^k(1-p)^{n-k} (kn)Pk(1−p)n−k
(其中 ( n r ) = n ! x ! ( n − x ! ) (^r_n)= \frac{n!}{x!(n-x!)} (nr)=x!(n−x!)n!) - 期望
np - 方差
n p ( 1 − p ) np(1-p) np(1−p)
- 几何分布
n个概率为p的独立可重复试验,直到第 n 次试验才第1次成功的概率分布- 公式
P P P { X = k X=k X=k}= ( 1 − p ) k − 1 (1-p)^{k-1} (1−p)k−1 - 期望
1/p - 方差
( 1 − p ) / p 2 (1-p)/p^2 (1−p)/p2
- 公式
泊松分布
- 泊松分布
- 定义
描述在单位时间内随机事件发生x次数的概率。事件在任意区间的期望和方差均为 λ \lambda λ,1小时内到达的汽车数为泊松分布,均值为10辆/小时, P ( X = k ) = 1 0 k k ! e − 10 P(X= k)=\frac{10^k}{k!}e^{-10} P(X=k)=k!10ke−10。 - 性质
任意两个相等长度的区间中,事件发生的概率相同。任意区间事件发生的保持独立。 - 公式
P ( X = k ) = λ k k ! e − λ P(X= k)=\frac{\lambda^k}{k!}e^{-\lambda} P(X=k)=k!λke−λ
- 定义
- 二元概率分布
两个随机变量,没对取值的概率。关注随机变量的关系。
超几何分布
- 超几何分布
- 定义:总体N有r个成功元素,不放回抽n次,恰好x次成功的概率。总量足够大时、近似于二项分布:次数n、成功率p = r/N
- 公式:
f ( x ) = ( n r ) ( n − x N − r ) ( n N ) f(x)= \frac{(^r_n)(^{N-r}_{n-x})}{(^N_n)} f(x)=(nN)(nr)(n−xN−r) (n:试验次数 x:成功次数 p:单次试验的成功概率, ( n r ) = n ! x ! ( n − x ! ) (^r_n)= \frac{n!}{x!(n-x!)} (nr)=x!(n−x!)n!) - 期望
E ( x ) = μ = n ( r N ) E(x)=\mu=n(\frac {r}{N}) E(x)=μ=n(Nr) - 方差
V a r ( x ) = σ 2 = n ( r N ) ( 1 − r N ) ( N − n N − 1 ) Var(x) =\sigma^2=n(\frac {r}{N})(1-\frac {r}{N})(\frac{N-n}{N-1}) Var(x)=σ2=n(Nr)(1−Nr)(N−1N−n)
- 公式:
- 负二项分布
所有成功r次即停止的实验中、失败次数k的分布
3. 连续概率分布
均匀概率分布
- 均匀概率分布
- 定义:理想的分布,概率与区间长度成正比,概率密度函数在结果区间内为固定的数值,
- 公式
f ( x ) = 1 b − a f(x)=\frac {1}{b-a} f(x)=b−a1 (a<x<b) - 图
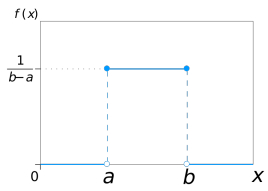
- 期望: ( a + b ) 2 \frac{(a+b)}{2} 2(a+b)
- 方差: ( a + b ) 2 12 \frac{(a+b)^2}{12} 12(a+b)2
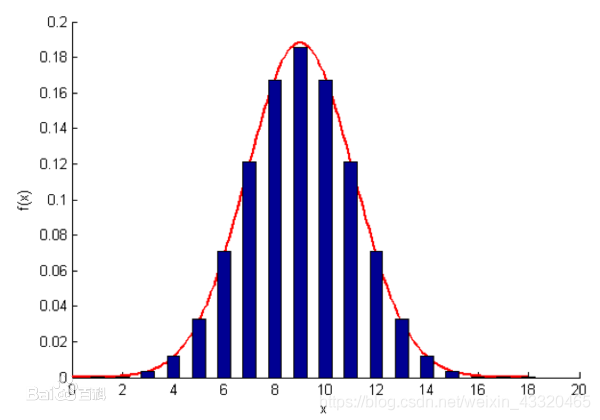
正态概率分布
- 正态概率分布
-
定义
常见的分布又称“常态分布”,又名高斯分布(Gaussian distribution)若随机变量X服从一个数学期望为μ、方差为 σ 2 σ^2 σ2的正态分布,记为N(μ,σ^2)。 -
特性:
其概率密度函数为正态分布,由曲线下方的面积构成,和为1;
期望值μ决定了其位置,位于曲线最高点,μ=中位数=众数,可以是任意值
其标准差σ决定了分布的幅度,σ越大曲线越宽越平坦。 -
公式
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 μ 2 f(x)=\frac{1}{\sigma \sqrt 2\pi}e^{- \frac{(x-\mu)^2}{2\mu ^2}} f(x)=σ2π1e−2μ2(x−μ)2
( μ = m e a n \mu=mean μ=mean, σ = s t a n d a r d d e v i a t i o n \sigma= standard deviation σ=standarddeviation, e = 2.7183 e=2.7183 e=2.7183) -
图
-
期望
μ \mu μ -
方差
σ 2 \sigma^2 σ2 -
特例 -标准正态分布
当μ = 0,σ = 1时的正态分布,概率密度函数为 f ( x ) = 1 2 π e − ( x ) 2 2 f(x)=\frac{1}{ \sqrt 2\pi}e^{- \frac{(x)^2}{2}} f(x)=2π1e−2(x)2 -
正态分布表
1、通查找实数x的位置,从而得到p(z<=x)。
2、表的纵向代表x的整数部分和小数点后第一位,横向代表x的小数点后第二位,然后就找到了x的位置。比如这个例子,纵向找2.0,横向找0,就找到了2.00的位置,查出0.9772。 -
经验法则
或称为“68-95-99.7法则”在实际应用上,常考虑一组数据具有近似于正态分布的概率分布。若其假设正确,则:
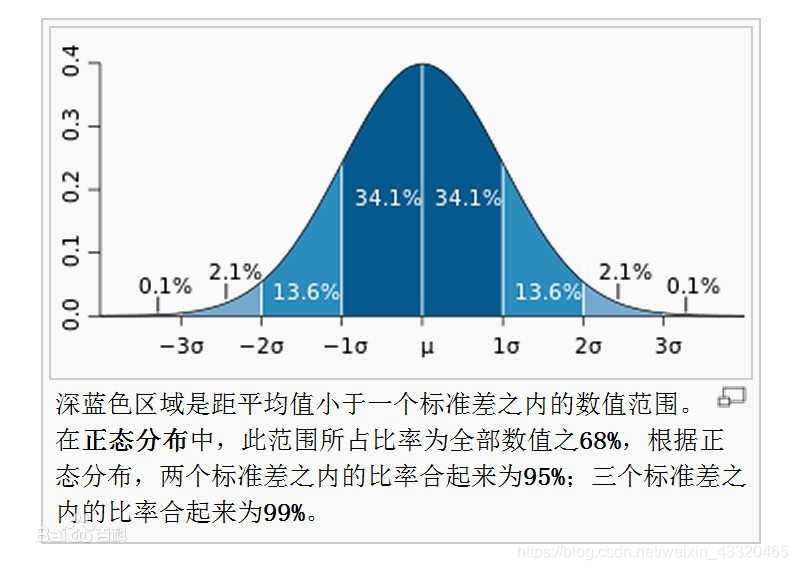
- 约68.3%数值分布在距离平均值有1个标准差之内的范围,
- 约95.4%数值分布在距离平均值有2个标准差之内的范围,
- 约99.7%数值分布在距离平均值有3个标准差之内的范围。
- 落在三个标准差之外的概率只有.0.27%.这个部分误差将不再属于随机误差而属于粗大误差
-
计算
转化为标正态分布 z = x − μ σ z =\frac{x-\mu}{\sigma} z=σx−μ -
举例:
例一:z服从n(0,1),求p(|z|≥2)。
由于z已经服从标准正态分布n(0,1),那么z’=z,不必转化了。
p(|z|≥2)=p(z≥2)+p(z<=-2)
=2p(z≥2)
=2(1-p(z<=2))
查表可知,p(z<=2)=0.9772,所以p(|z|≥2)=0.0456。
例二:z服从n(5,9),求p(z≥11)+p(z<=-1)。
令z’=(z-5)/3,z’服从n(0,1)
做转化p(z≥11)+p(z<=-1)=p(|z-5|≥6)
=p(|z’|≥2)
-
指数概率分布
- 指数概率分布
- 定义:连续两个事件发生的时间间隔服从指数分布,例如两辆汽车达到的时间0.1小时/辆, f ( X ) = 1 0.1 e − x 1 0.1 f(X)=\frac{1}{0.1}e^{-x\frac{1}{0.1}} f(X)=0.11e−x0.11
- 公式
- 概率密度函数
f ( X ) = λ e − λ x f(X)=\lambda e^{-\lambda x} f(X)=λe−λx (x大于0, λ = 1 / μ \lambda =1/\mu λ=1/μ) - 概率计算累积分布函数
F ( x ; λ ) = 1 − e − λ x F(x;\lambda)=1-e {-\lambda x} F(x;λ)=1−e−λx (x ≥ \geq ≥ 0)
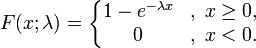
- 概率密度函数
- 图
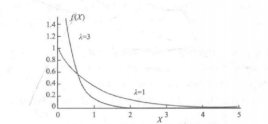
- 期望
1 λ \frac{1}{\lambda} λ1 - 方差
1 λ 2 \frac{1}{\lambda^2} λ21 - 特性
均值=标准差、右偏
- 幂律分布
4. 重要汇总
- 离散
- 二项分布: n次独立试验中 x次「成功」的概率
- 泊松分布 :特定时间段或空间中 事件发生x次的概率
- 超几何分布 :n次相互关联试验中 X次「成功」的概率
- 连续
- 均匀概率分布 :随机变量 取值概率相同在「等长度的区间」上
- 正态概率分布 :钟形概率密度函数 由均值μ和标准差σ确定
- 指数概率分布 :用于计算 完成一项任务所需时间的概率
5抽样分布
1. 基础知识
- 基础概念
- 抽样估计 :利用样本指标估计总体指标
- 总体:根据研究业务逻辑和研究需要确定 的对象全体
- 有\无限总体:
在无放回抽样时,对于有限总体与无限总体其统计量的分布是不同的。在无限总体的情况下,每次抽取一个样本并不影响下一次的抽取,因此可以看作是独立的。而对于有限总体每一次抽选的结果将影响到下一次的抽选结果。 - 总体参数:总体的数据特征: 平均数、比重结构
- 样本: 随机从总体中抽取 的部分个体。特别澄清一点的是把样本想象成固定的会限制我们的思考。总体和样本的关系是一对多的
- 样本指标(统计量):样本特征(平均数、方差)用来估计总体参数
- 样本容量 个体的数目
- 样本个数 总体中抽样的次数
- 点估计(point estimation):用样本统计量来估计总体参数
- 点估计量:样本统计量
- 点估计值:点估计量的值
- 无偏估计量:数学期望等于被估计的量的统计估计量称为无偏估计量。
- 无偏性:估计量的均值(数学期望)应等于未知参数的真值。
- 统计推断
利用样本信息对总体性质建立估计 检验假设 - 抽样方法
单随机抽样
分层随机抽样,每一层内方差相对小
整群抽样
系统抽样,通常假定具有简单随机抽样的性质
方便抽样,非概率抽样
判断抽样,非概率抽样 - 拟合度
抽样结果与总体特征的接近程度 - 抽样分布
是指样本估计量的分布,「随机变量」的「概率分布」 - 抽样误差
无偏估计量的值与对应总体参数之差的绝对值
利用样本统计量的抽样分布,能对抽样误差进行概率描述 - 标准误差
样本的标准差 - 有限总体修正系数
无放回抽样时:在通常的情况下有限总体统计量的方差小于无限总体抽样时的方差,需要乘上—个系数1-n/N,称为有限总体的修正系数,简写为fpc。
由于n<N,因此1-n/N总是小于1,若抽样的比例很小,即n/N小于0.05时,有限总体修正系数就可以忽略不计 [1] 。
2.抽样
- 样本
- 简单随机采样
- 定义:从容量为N的有限总体中,以相同概率抽取n个作为一个样本。常见无返回抽样,也有放回抽样
- 随机采样
- 定义:从无限的总体中,独立抽取n个样本
- 简单随机采样
点估计
- 点估计
-定义:推断统计的一种, 用样本统计量来估计总体参数,样本统计量就是总体参数的点估计。- 良好点估计量的特征
- 无偏性 :样本统计量的期望等于总体的参数
- 一致性 :当样本容量增大,点估计值接近总体参数, 估计效果越好
- 有效性 :标准差越小,估计量更有效,统计量的抽样分布小
- 良好点估计量的特征
中心极限定理
- 中心极限定理
- 定义
简单随机采样从整体中抽取容量为n的样本,当样本足够大(大于30)时,样本平均值的分布趋于正态分布,方差随着实验次数增加而减小。 - 适用
任何总体。一种量足够大的样本,无论服从什么分布,最终都能转化为正态分布。当样本严重偏态时可以扩大样本 - 价值:
- 为数理统计学和误差分析提供了理论基础,指出了大量随机变量近似服从正态分布的条件。这种方法在数理统计中用得很普遍,当处理大样本时,它是重要工具。
- 在实际工作中有广泛的实际应用背景。只要n足够大,便可以把独立同分布的随机变量之和当作正态变量。例如:AB-TEST
- 在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。
- 定义
3.抽样分布
- 定义
样本统计量的所有可能值构成的概率分布 - 内涵
重复抽样过程n次,得到的样本统计量的概率分布。用于样本统计量和总体参数进行概率描述 - 注意
?已知总体均值及方差 - 样本均值的抽样分布
- 定义 :样本均值的可能值的概率分布
- 期望
E ( x ‾ ) = μ E(\overline {x})=\mu E(x)=μ,无偏估计量 - 标准差
均值的误差标准,点估计量(样本均值)的标准差,用于确定样本均值和总体均值的偏离程度- 有限总体
-
一般情况,考虑修正系数
σ x ‾ = N − n N − 1 ( σ n ) \sigma_{\overline{x}} =\sqrt{\frac {N-n}{N-1}}\bigg(\frac{\sigma}{\sqrt n}\bigg) σx=N−1N−n(nσ) -
总体量大, n / N ≤ 0.05 n/N\le 0.05 n/N≤0.05,实际情况总是假定总体容量较大
σ x ‾ = σ n \sigma_{\overline{x}} =\frac{\sigma}{\sqrt n} σx=nσ
-
- 无限总体
- σ x ‾ = σ n \sigma_{\overline{x}} =\frac{\sigma}{\sqrt n} σx=nσ
- 有限总体
- 抽样分布形式
- 总体样本服从正态分布,则任何容量都符合正态分布
- 总体样本不服从正态分布则应用中心极限定理,样本容量很大时,金丝服从正态分布
- 样本比例的抽样分布
- 定义:样本比例抽样分布(sampling distribution of ratio)是从总体中重复随机抽取容量为n的所有样本,其样本比例的概率分布。比例是一个常用统计指标,如产品合格率、某群体学生考试成绩及格率、社会适龄人员就业率等。随样本容量的增加,样本比例抽样分布趋近于正态分布。
- E ( P ‾ ) = p E(\overline P)=p E(P)=p 总体中具有某一特征单位数占总体全部单位数的比例称为总体比率,用P表示;样本中具有某一特征的单位数占样本全部单位数的比例称为样本比例,用p表示。
- 标准差
比例的标准误差,点估计量(样本比例)的标准差,用于确定样本比例和总体均值的接近程度- 有限总体
-
一般情况,考虑修正系数
σ p ‾ = N − n N − 1 p ( 1 − p ) n \sigma_{\overline{p}} =\sqrt{\frac {N-n}{N-1}}\sqrt{\frac{p(1-p)}{ n}} σp=N−1N−nnp(1−p) -
总体量大, n / N ≤ 0.05 n/N\le 0.05 n/N≤0.05,实际情况总是假定总体容量较大
σ p ‾ = p ( 1 − p ) n \sigma_{\overline{p}} =\sqrt{\frac{p(1-p)}{ n}} σp=np(1−p)
-
- 无限总体
- σ p ‾ = p ( 1 − p ) n \sigma_{\overline{p}} =\sqrt{\frac{p(1-p)}{ n}} σp=np(1−p)
- 抽样分布形式
离散概率分布。样本中具有被关注特征的个体数目x 服从二项分布,n为常数,故x/n也服从二项分布。近似正态分布的判断条件: n p ′ np\rq np′
- 有限总体
6区间估计
总结
- 一个总体参数的区间估计

2.两个总体参数的区间估计
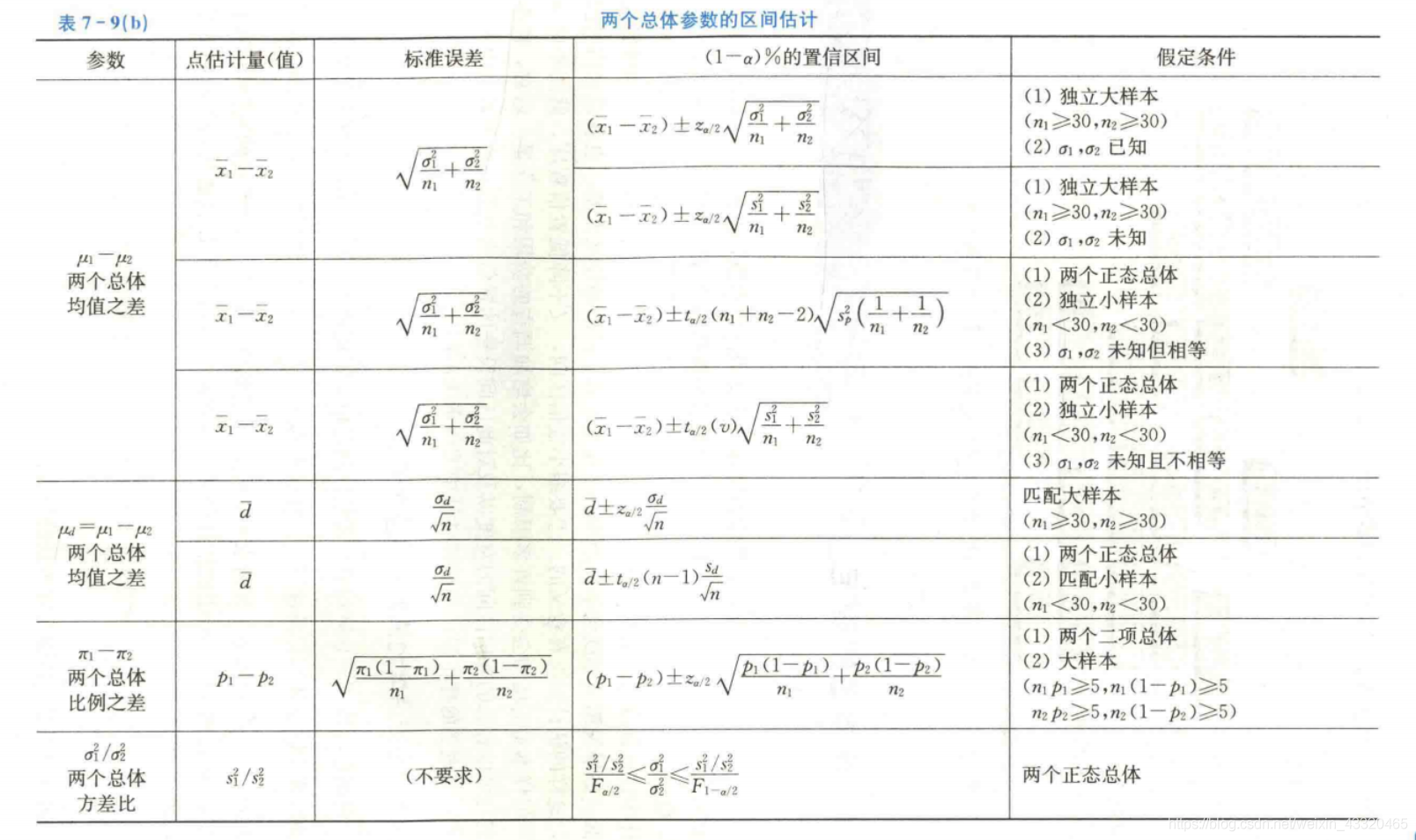
1.基础
置信区间估计
-
区间估计(interval estimate)
一种总体参数的估计方法,在点估计的基础上,给出总体参数估计的一个区间范围,该区间通常由样本统计量加减估计误差得到。 -
与点估计不同
能提供估计精确的信息,估计值与总体参数的接近程度,更适用。进行区间估计时,根据样本统计量的抽样分布可以对样本统计量与总体参数的接近程度给出一个概率度量 -
构建
点估计值 ± \pm ±边际误差- 边际误差
抽样误差的上下限,等于临界值乘以统计量的分布标准差
案例:
总体平均值的区间估计: x ‾ ± \overline x\pm x± Margin of error
总体比例的区间估计: p ‾ ± \overline p\pm p± Margin of error
- 边际误差
-
置信区间
指由样本统计量所构造的总体参数的估计区间(误差范围). 设置范围的目的是为了满足某一置信水平。置信区间越大,置信水平越高。-
置信度
指构造总体参数的多个样本区间中,包含总体参数的区间占总区间数的概率,一般用1-α表示;可以理解为:特定个体对待特定命题真实性相信的程度。α成为显著性水平,通常取值0.025、0.05、0.1,对应0.975、0.95、0.9
解释:
1.用中括号[a,b]表示样本估计总体平均值的误差范围的区间[a,b]被称为置信区间。“a和b之间包含总体平均值”的概率,这个概率就是置信水平。
2.95%的置信水平 ,适用区间估计法得到的全部
[a,b]区间中,如果有95%的区间包含总体参数 -
置信区间的宽度
计算公式为:b-a,较窄的置信区间比较宽的置信区间能提供更多的有关总体参数的信息
估计全班均值:区间 间隔 宽窄度 表达的意思 100分 100 宽 等于什么也没告诉你 30-80分 50 较窄 你能估出大概的平均分了(55分) 60-70分 10 窄 你几乎能判定全班的平均分了(65分) -
计算:
- 样本数据,其容量n,平均值为μ,标准偏差为σ,则其整体数据的平均值的100(1-α)%置信区间为
μ ± Z α / 2 σ x ‾ \mu\pm Z_{\alpha/2}\sigma_{\overline x} μ±Zα/2σx (α为非置信水平在正态分布内的覆盖面积 , Z α / 2 Z_{\alpha/2} Zα/2即为对应的标准分数, σ x ‾ = σ n \sigma_{\overline x}=\frac{\sigma}{\sqrt n} σx=nσ)
- 样本数据,其容量n,平均值为μ,标准偏差为σ,则其整体数据的平均值的100(1-α)%置信区间为
-
当置信度为0.95,对应σ/2=0.025,即需要查1-0.025=0.975对应的Z值为1.96,对应正态分布表
-
影响因素
从公式可以看出置信水平、样本量等因素均有关系,其中:- 样本量:在置信水平固定的情况下,样本量越多,置信区间越窄。
- 置信水平,在样本量相同的情况下,置信水平越高,置信区间越宽。
-
-
常用置信水平
90% 、95%,99%,为了简化运算通常取对应的z值为:1,2,3 -
想要达到较高的置信水平
- 增大边际误差
- 增大置信区间的宽度
2.总体均值
- 总体标准差
- 已知
采用置信系数 , μ ± Z α / 2 σ n \mu\pm Z_{\alpha/2}\frac{\sigma}{\sqrt n} μ±Zα/2nσ - 未知:t分布 μ ± t α / 2 σ n \mu\pm t_{\alpha/2}\frac{\sigma}{\sqrt n} μ±tα/2nσ
- 已知
- 如何确定样本容量
根据 E = μ ± z α / 2 σ n E= \mu\pm z_{\alpha/2}\frac{\sigma}{\sqrt n} E=μ±zα/2nσ 倒推:
n = ( Z α / 2 ) σ 2 E 2 n=\frac{(Z_{\alpha/2})\sigma^2}{E^2} n=E2(Zα/2)σ2
步骤:- 确定可以接受的边际误差E
- 给定置信度α
- 根据公式计算n
- 影响区间估计质量的因素
- 总体分布
- 当分布是正态分布时,无论样本量,均为精确估计。为非正态分布时,均为近似估计(与正态分布),考虑样本量
- 样本量
- 大于30 ,按照中心极限定理可以将一般的抽样分布的样本看为正态分布。对于偏度大或者有异常的数据可以增加样本量至50以上
- 小于30,如果总体分布为正态则可按照正态处理。小于30 ,增加样本再应用中心极限定理
- 样本
- 容量越大、越近似程度越大越好
- 总体分布
t 分布
- 定义
t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。
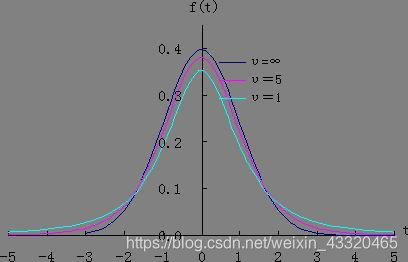
- 特点
- 前提假设 抽样总体呈正态分布,或者样本容量足够大
- 均值为0 ,一系列类似的分布,单峰分布
- 与n(确切地说与自由度df)大小有关
- 一个自由度,对应唯一t分布
- 自由度越大变异程度越小,越接近标准正态分布,自由度df越小,t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;当自由度df=∞时,t分布曲线为标准正态分布曲线。
- 类似标准正态表 可以查t值
- 公式
μ ± t α / 2 σ n \mu\pm t_{\alpha/2}\frac{\sigma}{\sqrt n} μ±tα/2nσ ( s = ∑ ( x i − x ‾ ) 2 n − 1 s=\sqrt{\frac{\sum(x_i-\overline x)^2}{n-1}} s=n−1∑(xi−x)2,n-1 :自由度,1-σ:置信度)
3.总体比率
- 总体比例是指总体中具有某一相同标志表现的全部总体单位数的比重
- 公式: p ‾ ± z α / 2 p ‾ ( 1 − p ‾ ) n \overline p \pm z_{\alpha/2}\sqrt\frac{\overline p (1-\overline p )}{ n} p±zα/2np(1−p)
- 案例:某城市想要估计下岗职工中女性所占的比例,随机抽取了100个下岗职工,其中65人为女职工。试以95%的置信水平估计该城市下岗职工中女性比例的置信区间

- 如何确定样本容量
根据 p ‾ ± z α / 2 p ‾ ( 1 − p ‾ ) n \overline p \pm z_{\alpha/2}\sqrt\frac{\overline p (1-\overline p )}{ n} p±zα/2np(1−p) 倒推:
n = ( Z α / 2 ) p ‾ ∗ ( 1 − p ‾ ∗ ) E 2 n=\frac{(Z_{\alpha/2})\overline p^* (1-\overline p^* )}{E^2} n=E2(Zα/2)p∗(1−p∗),
4.汇总:
- 一个总体参数估计的不同情形及使用的分布

- 样本应用建议
- 总体正态 ,任意样本容量,可以n ≤ 15 \leq15 ≤15
- 一般情况,n ≥ 30 \geq30 ≥30
- 存在异常,严重倾斜,n ≥ 50 \geq50 ≥50
- 非正态但对称分布,n ≥ 15 \geq15 ≥15
7假设检验
- 假设
推论统计中用于检验统计假设的一种方式,判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。 - 假设检验基本原理
依据小概率原理,先假设总体参数的某项取值为真,然后通过抽样研究的统计推理抽取一个样本进行观察,如果样本信息显示出现了与事先假设相反的结果且与原假设差别很大,则说明原来假定的小概率事件在一次实验中发生了,这是一个违背小概率原理的不合理现象,因此有理由怀疑和拒绝原假设;否则不能拒绝原假设。- 小概率原理
发生概率很小的随机事件(小概率事件)在一次实验中几乎是不可能发生的。
- 小概率原理
1.建立假设
- 拒绝域
拒绝域亦称否定域,又称临界域,指在假设检验中,能够拒绝原假设的检验统计量的所有可能取值的取值范围,称为拒绝域。
就是显著性水平α所围成的区域。假设检验中根据检验统计量的分布,由给定的小概率α(0<α<1)作为显著性水平所确定的拒绝原假设H0的区间称为拒绝域,即统计量在其中取值的概率为α的区域。 - 接受域
不能够拒绝原假设的检验统计量的所有可能取值的集合称为接受域; - 临界值
根据给定的显著性水平确定的拒绝域的边界值,称为临界值 - 原假设
H0,零假设,尝试性的假定为真的假设
H0:支持骑自行车出入是应该下车的人不足10% - 备假设
H1,实际需要证明的,与原假设完全对立,如果原假设被拒绝,则被认为是真的假设。
H1:支持骑自行车出入是应该下车的人足10% - 如何选择
- 一般将检验「试图建立」的结果设为「备择假设」
- 案例
- 研究中的假设
设为H1备择假设,如果原假设被拒绝,则研究中的假设为真 ,结论从统计上,支持研究者。 - 受到挑战的假说
设为H0原假设,如果原假设被拒绝,该假说不正确。结论从统计上,反对假说 - 决策支持中的检验
不一定,前面两种情况都存在,如Ho被拒绝,将采取措施。决策时两种情况「都要」采取措施
- 研究中的假设
- 形式
等号总在原假设中- 单侧检验
- 下侧检验
H 0 : μ ≥ μ 0 H_0:\mu \geq \mu_0 H0:μ≥μ0
H 1 : μ < μ 0 H_1:\mu <\mu_0 H1:μ<μ0 - 上侧检验
H 0 : μ ≤ μ 0 H_0:\mu \leq \mu_0 H0:μ≤μ0
H 1 : μ > μ 0 H_1:\mu >\mu_0 H1:μ>μ0
- 下侧检验
- 双侧检验
H 0 : μ = μ 0 H_0:\mu =\mu_0 H0:μ=μ0
H 1 : μ ≠ μ 0 H_1:\mu \neq\mu_0 H1:μ=μ0
- 单侧检验
2.两类错误
-
原因:假设检验建立在「样本信息」的基础上,有误差
- 预测为正例 预测为负例 实际为正例 TP:True Positive。 FN:False Negative 实际为负例 FP:False Positive TN:True Negative - 正例反例
是一个相对概念。正想里通常我是我们所关注的结果。 - 精确率precision,TP/(TP+FP)
预测为正例的正确率。实际问题中更关注准确率,样本的正负例分布并不均匀。 - 召回率recall,TP/(TP+FN)
实际为正例的正确率 - 正确率,(TP+TN)/(TP+FP+FP+TN)
判断的总正确率
- 正例反例
-
两类错误
在样本容量(n)不变的前提下,两者不能同时变小,减小α必然导致β增大;反之,减小β必然导致α增大,两者呈反向变动关系,图1
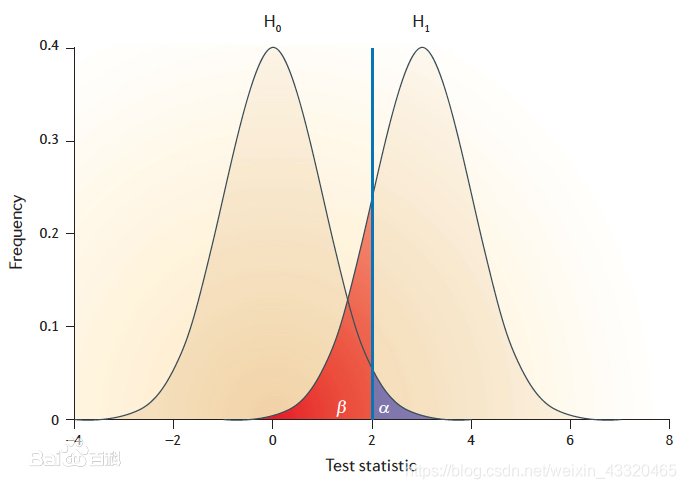
- 第一类错误
- 定义:FN,拒绝了H0但H0(原假设)为真,假阳性(阳性代表有,假阳性代表假有效)。药品是否安全:第一类错误,准许了不安全的药品投入使用
- 显著性水平
- 定义:当原假设为真成立时,犯第一类错误的概率。每一个样本都会计算出一个样本均数,每一个样本均数其实都是X轴上的一个点,有的样本均数离总体均数近,而有的离总体均数远。当我们抽中的样本计算出来的样本均数离总体均数远的时候,即两者差异较大时,我们就会倾向拒绝两者相等的假设。所以,即便实际上H0假设正确,数轴上依然会有一些点与总体均数的距离较远,当这些点对应的样本被我们抽中时,我们就会做出拒绝H0的决定,从而我们就会犯错了,这便是第一类错误的发生逻辑。
- 设定
发生第一类错误的概率最大允许值。由进行假设检验的人设定 - 表示
α ,一般为0.05或0.01。例如:在实验研究中的,假设H0通常为因素间无关中,当α 越小,实验差异越显著,意味着拒绝H0的错误很小,可以拒绝H0,则H1成立。
- 显著性检验
只控制第一类错误的假设检验
- 第二类错误
- 定义:FP,接受了H0但H0为假,假阴性(假无效)。药品是否安全:第二类错误,拒绝了安全的药品投入使用
- 设定
通过预先设定显著性水平和检验效能可以计算出实验所需要的最小样本量。这也是ab test的基础。 - 表示
β。α固定的情况下,需要增大样本容减少𝛃发生的概率。犯第二类错误,那么意味着H0(总体平均身高为1.8m)是假的,实际上可能是1.85m。这其中会出现一个比较绕的点是,由于H0和事实不一致,所以H0所代表的总体和实际研究的总体也不一样。当我们计算犯错概率时,用的是第二个实际总体,即我们这个样本并不是来自第一个总体,而是来自第二个实际的总体,
- 第一类错误
2.一般步骤
- 建立 H 0 H_0 H0与 H 1 H_1 H1
- 制定显著性水平 α
若第一类错误的成本很高,设置较小值,不高则设置较大值 - 根据样本数据计算检验统计量
- 选择拒绝法则
- p—value
如果p—value 小于等于α,拒绝 H 0 H_0 H0 - 临界值法
利用α确定临界值,比较检验统计量和临界值,确定是否拒绝 H 0 H_0 H0
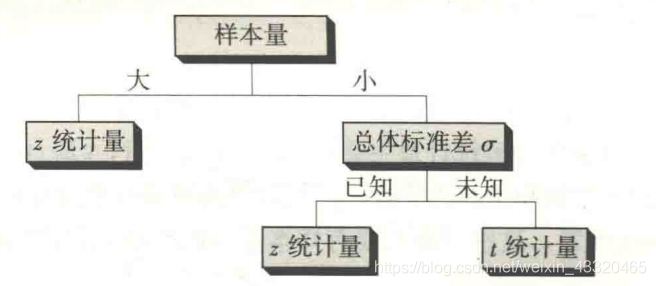
- p—value
检验统计量的确定
3.均值第二类错误概率计算
- 步骤
- 建立原假设和备择假
- 在显著性水平α下,确定「临界值」,建立「拒绝规则」,计算 Z Z Z
- 求解与「临界值」对应的「样本均值」 x ‾ \overline x x 根据 Z = x ‾ − μ 0 σ / n Z=\frac{\overline x-\mu_0}{\sigma/\sqrt n} Z=σ/nx−μ0, E = μ ± z α / 2 σ n E= \mu\pm z_{\alpha/2}\frac{\sigma}{\sqrt n} E=μ±zα/2nσ
- 得到:接受H0时对应的「样本均值」的值,构成接受域
- 对于满足「备择假设」的μ值,计算μ落在「接受域」的概率z,根据 Z = x ‾ − μ 0 σ / n Z=\frac{\overline x-\mu_0}{\sigma/\sqrt n} Z=σ/nx−μ0,根据Z,计算得到概率β
- 作用
- 当H0为假时,拒绝H0的概率,即1-β。
- 案例

解读:
- 求两类错误的概率 就是求放入正态中求 α \alpha α 和 β \beta β
- 求第一类错误,落在H0拒绝域内,使用题目中的拒绝域是相对于原假设的,所以求在H0中大于2.6的概率。简化为放入H0的正态的中求2.6边际后的面积
- 求第二类错误,落在H0的接受域H1的拒绝域中,由于H0所代表的总体和实际研究的总体也不一样,计算犯错概率时,用的是(H1)实际总体,所以求在H1中小于2.6的概率。简化为放入H0的正态的中求面积,2.6之前后的面积
- 后面的转化其实只计算后半部分, Z β / 2 = x ‾ − μ 0 σ / n Z_{\beta/2}=\frac{\overline x-\mu_0}{\sigma/\sqrt n} Zβ/2=σ/nx−μ0化为正态计算, Φ \Phi Φ用老表示 Z β / 2 逆 运 算 Z_{\beta/2}逆运算 Zβ/2逆运算,
4.总体均值假设检验
总体均值假设检验结合区间估计中总体均值的计算:大样本数据可以直接选用Z统计量,小样本按照总体标准差是否已知分为两种情况。计算的公式可以由区间估计倒推。
- 分类
- 总体
σ
\sigma
σ未知
- 检验统计量 t t = x ‾ − μ 0 s / n t=\frac{\overline x - \mu_0}{s/\sqrt n} t=s/nx−μ0
- 案例:某机器制造出的肥皂厚度为5cm,今欲了解机器性能是否良好,随机抽取10块肥皂作为样本,测得平均厚度为5.3cm,标准差为0.3cm,试以0.05的显著性水平检验机器性能良好的假设。

- 总体
σ
\sigma
σ已知
- 检验统计量 z z = x ‾ − μ 0 s / n z=\frac{\overline x - \mu_0}{s/\sqrt n} z=s/nx−μ0
- 双侧检验
- 形式: H 0 : μ = μ 0 , H 1 : μ ≠ 1 μ 0 H_0:\mu=\mu_0,H_1:\mu\ne1\mu_0 H0:μ=μ0,H1:μ=1μ0
- 拒绝法则
- 临界值法则
计算Z, ∣ Z ∣ ≥ Z α / 2 |Z|\geq Z_{\alpha/2} ∣Z∣≥Zα/2任意一个成立即可拒绝原假设 - P-value
定义:如果原假设成立,出现样本观察结果或者更极端值出现的概率。实际就是依据Z,进一步计算α 。如果值小于α,拒绝原假设。
P经验解读:强有力的证据<0.01、有力证据0.01-0.05、弱证据0.05-0.10、>0.10没有足够的证据
计算:带入公式: Z = x ‾ − μ 0 σ / n Z=\frac{\overline x-\mu_0}{\sigma/\sqrt n} Z=σ/nx−μ0检验统计量的值Z,P-value=面积(1-ϕ(Z))*2.(*2是因为Z实际是 Z α / 2 Z_{\alpha/2} Zα/2)
- 临界值法则
- 单侧检验
实际中的问题带有方向性,1.越大越好:寿命 2.越小越好,成本- 形式
H 0 : μ ≤ μ 0 , H 1 : μ > μ 0 H_0:\mu\leq \mu_0,H_1:\mu>\mu_0 H0:μ≤μ0,H1:μ>μ0; H 0 : μ ≥ μ 0 , H 1 : μ < μ 0 H_0:\mu\geq \mu_0,H_1:\mu<\mu_0 H0:μ≥μ0,H1:μ<μ0, - 拒绝法则
- P-value
定义:如果p值小于α/2,拒绝原假设。
计算:带入公式: Z = x ‾ − μ 0 σ / n Z=\frac{\overline x-\mu_0}{\sigma/\sqrt n} Z=σ/nx−μ0检验统计量的值Z,P-value=面积 1-Z - 临界值法则
计算Z,右检验 Z ≥ Z α / 2 Z\geq Z_{\alpha/2} Z≥Zα/2或者左检验 Z ≤ − Z α / 2 Z\leq -Z_{\alpha/2} Z≤−Zα/2
- P-value
- 形式
- 总体
σ
\sigma
σ未知
- 检验结果质量影响因素
与6.2同 :影响区间估计质量的因素,案例《统计学8章8.6》 - 如何确定样本容量
1.前提:同时控制一类和第二类错误
2.1 单侧检验: n = ( Z α + Z β ) 2 σ 2 ( μ 0 − μ a ) 2 n=\frac{(Z_\alpha+Z_\beta)^2\sigma^2}{(\mu_0-\mu_a)^2} n=(μ0−μa)2(Zα+Zβ)2σ2
2.2双侧检验
Z α / 2 Z_{\alpha/2} Zα/2替换 Z α Z_\alpha Zα
3. α β n \alpha\beta n αβn已知两个可以计算第三个
5.总体比率
- 形式
- 双侧: H 0 : p = p 0 , H 1 : p ≠ p 0 H_0:p=p_0,H_1:p\neq p_0 H0:p=p0,H1:p=p0
- 单侧:
H 0 : p ≤ p 0 , H 1 : p > p 0 H_0:p\leq p_0,H_1:p>p_0 H0:p≤p0,H1:p>p0; H 0 : p ≥ p 0 , H 1 : p < p 0 H_0:p\geq p_0,H_1:p<p_0 H0:p≥p0,H1:p<p0,
- 前提
- 只讨论大样本情况, n ( 1 − p ) ≥ 5 n(1-p)\geq 5 n(1−p)≥5或 n p ≥ 5 np\geq5 np≥5,此时比例p的抽样,分布可以用正态分布近似
- 检验统计量计算:
z = p ‾ − p 0 p 0 ( 1 − p 0 ) n z=\frac{\overline p-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} z=np0(1−p0)p−p0,来源于: p ‾ ± z α / 2 p ‾ ( 1 − p ‾ ) n \overline p \pm z_{\alpha/2}\sqrt\frac{\overline p (1-\overline p )}{ n} p±zα/2np(1−p), p ‾ 0 为 总 体 比 例 P 的 假 设 值 \overline p_0为总体比例P的假设值 p0为总体比例P的假设值
- 案例:
一项统计结果声称,某市老年人口(年龄在65岁以上)所占的比例为14.7%,该市老年人口研究会为了检验该项统计是否可靠,随机抽选了400名居民,发现其中有57人年龄在65岁以上。调查结果是否支持该市老年人口比例为14.7%的看法(a=0.05)?

- 高阶
-
p
‾
\overline p
p的精确分布抽样,
- 本质是离散分布,样本量足够大时,可二项分布可以转化为正态分布近似求解。由二项分布给出 p ‾ \overline p p的每个取值概率
- 小样本
- 不能采用正态近似则改用精确统计分布,实际中很少出现总体比例的小样本检测,有关比例的问题往往需要大样本量来保证结果的稳定性。
-
p
‾
\overline p
p的精确分布抽样,
8 两总体均值之差和比例之差的推断
对于两个总体,所关心的参数主要有两个总体的均值 之差 μ 1 − μ 2 \mu_1-\mu_2 μ1−μ2、两个总体的比例之差, p 1 − p 2 p_1-p_2 p1−p2、两个总体的方差比 σ 1 2 / σ 2 2 \sigma^2_1/\sigma^2_2 σ12/σ22等
均值样本之差 - 独立样本
- 独立样本( independent sample)
如果两个样本是从两个总体中独立抽取的,即一个样本中的元素与另一个样本中的元素相互独立,则称为独立样本。如果两个总体都为正态分布,或两 - 前提
两个总体都服从正态分布或者样本量足够大。
两个样本 x ‾ 1 a n d x ‾ 2 \overline x_1and \overline x_2 x1andx2近似服从正态分布, x ‾ 1 − x ‾ 2 \overline x_1- \overline x_2 x1−x2服从 μ ‾ 1 − μ ‾ 2 \overline \mu_1- \overline \mu_2 μ1−μ2的正态分布,方差: σ x ‾ 1 − x ‾ 2 = σ 1 2 n 1 + σ 2 2 n 2 \sigma_{\overline x_1- \overline x_2}=\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}} σx1−x2=n1σ12+n2σ22,即:
z = ( x ‾ 1 − x ‾ 2 ) − ( μ ‾ 1 − μ ‾ 2 ) σ 1 2 n 1 + σ 2 2 n 2 服 从 N ( 0 , 1 ) z=\frac{(\overline x_1- \overline x_2)-(\overline \mu_1- \overline \mu_2)}{\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}} 服从N(0,1) z=n1σ12+n2σ22(x1−x2)−(μ1−μ2)服从N(0,1) - 汇总
- 两个总体参数估计的不同情形及使用的分布

- 样本量
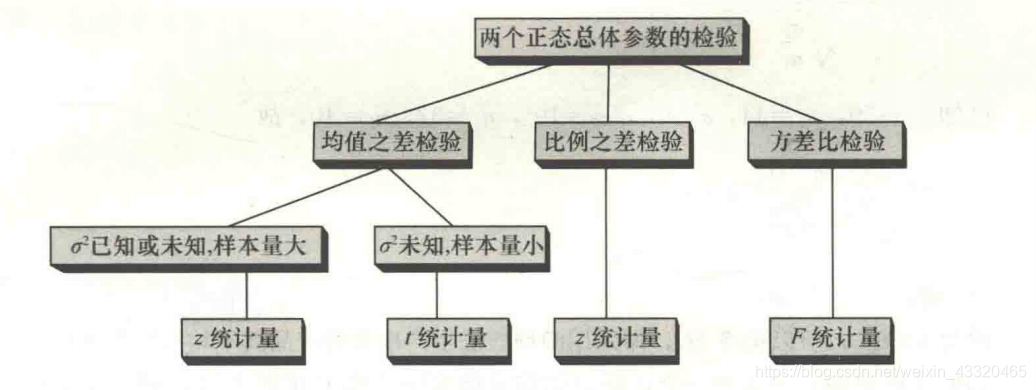
发样本 n 1 & n 2 ≥ 30 n_1\&n_2\geq30 n1&n2≥30,抽样分布分近似正态,如果样本量小于30必须满足正态分布。 - 两个正态总体参数的检验
- 两个总体参数估计的不同情形及使用的分布
-
已知 σ 1 , σ 2 \sigma_1,\sigma_2 σ1,σ2,基于Z分布
- 区间估计
( x ‾ 1 − x ‾ 2 ) ± z α / 2 σ 1 2 n 1 + σ 2 2 n 2 (\overline x_1- \overline x_2)\pm z_{\alpha/2}\sqrt{{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}} (x1−x2)±zα/2n1σ12+n2σ22
(当总体的方差 σ 1 2 , σ 2 2 \sigma^2_1,\sigma^2_2 σ12,σ22未知时用样本方差代替: ( x ‾ 1 − x ‾ 2 ) ± z α / 2 s 1 2 n 1 + s 2 2 n 2 (\overline x_1- \overline x_2)\pm z_{\alpha/2}\sqrt{{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}} (x1−x2)±zα/2n1s12+n2s22 )- 案例:
 即8±2.97=(5.03,10.97),两所中学高考英语平均分数之差的95%的置信区间为5.03~10.97分
即8±2.97=(5.03,10.97),两所中学高考英语平均分数之差的95%的置信区间为5.03~10.97分
- 案例:
- 假设检验
- 形式 : H 0 : μ 1 − μ 2 ≥ D 0 , : μ 1 − μ 2 < D 0 H_0:\mu_1-\mu_2\geq D_0,:\mu_1-\mu_2< D_0 H0:μ1−μ2≥D0,:μ1−μ2<D0; H 0 : μ 1 − μ 2 ≤ D 0 , : μ 1 − μ 2 > D 0 H_0:\mu_1-\mu_2\leq D_0,:\mu_1-\mu_2> D_0 H0:μ1−μ2≤D0,:μ1−μ2>D0; H 0 : μ 1 − μ 2 = D 0 , : μ 1 − μ 2 ≠ D 0 H_0:\mu_1-\mu_2= D_0,:\mu_1-\mu_2\neq D_0 H0:μ1−μ2=D0,:μ1−μ2=D0;
- 检验统计量
Z = ( x ‾ 1 − x ‾ 2 ) − D 0 σ 1 2 n 1 + σ 2 2 n 2 Z=\frac{(\overline x_1-\overline x_2)-D_0}{\sqrt{{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}}}} Z=n1σ12+n2σ22(x1−x2)−D0 - 案例
有两种方法可用于制造某种以抗拉强度为重要特征的产品。根据以往的资料得知,第一种方法生产出的产品抗拉强度的标准差为8千克,第二种方法的标准差为10千克。从采用两种方法生产的产品中各抽一个随机样本,样本量分别为n1=32,n2=40,测得x1=50千克x2=44千克。问采用这两种方法生产出来的产品平均抗拉强度是否有显著差别(a=0.05)?

- 区间估计
-
未知 σ 1 , σ 2 \sigma_1,\sigma_2 σ1,σ2,大样本,基于Z统计,
- 区间估计
当总体的方差 σ 1 2 , σ 2 2 \sigma^2_1,\sigma^2_2 σ12,σ22未知时用样本方差代替: ( x ‾ 1 − x ‾ 2 ) ± t α / 2 s 1 2 n 1 + s 2 2 n 2 (\overline x_1- \overline x_2)\pm t_{\alpha/2}\sqrt{{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}} (x1−x2)±tα/2n1s12+n2s22 ) - 合并样本的方差
- 区间估计
-
未知 σ 1 , σ 2 \sigma_1,\sigma_2 σ1,σ2,小样本,t统计自由度、合并样本方差计算方式不同,
-
σ 1 = σ 2 \sigma_1=\sigma_2 σ1=σ2,置信区间,计算合并样本方差、自由度能直接得出

案例:

-
σ 1 ≠ σ 2 \sigma_1\neq\sigma_2 σ1=σ2,置信区间,计算自由度、样本方差能直接带入

案例 - 假设检验 ,小样本, 未知
σ
1
,
σ
2
\sigma_1,\sigma_2
σ1,σ2
- 假设检验 ,小样本, 未知
σ
1
,
σ
2
\sigma_1,\sigma_2
σ1,σ2- 形式 : H 0 : μ 1 − μ 2 ≥ D 0 , : μ 1 − μ 2 < D 0 H_0:\mu_1-\mu_2\geq D_0,:\mu_1-\mu_2< D_0 H0:μ1−μ2≥D0,:μ1−μ2<D0; H 0 : μ 1 − μ 2 ≤ D 0 , : μ 1 − μ 2 > D 0 H_0:\mu_1-\mu_2\leq D_0,:\mu_1-\mu_2> D_0 H0:μ1−μ2≤D0,:μ1−μ2>D0; H 0 : μ 1 − μ 2 = D 0 , : μ 1 − μ 2 ≠ D 0 H_0:\mu_1-\mu_2= D_0,:\mu_1-\mu_2\neq D_0 H0:μ1−μ2=D0,:μ1−μ2=D0; - 检验统计量 t = ( x ‾ 1 − x ‾ 2 ) − D 0 s 1 2 n 1 + s 2 2 n 2 t=\frac{(\overline x_1-\overline x_2)-D_0}{\sqrt{{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}}} t=n1s12+n2s22(x1−x2)−D0
- 自由度
d f = ( s 1 2 n 1 + s 2 2 n 2 ) 2 1 n 1 − 1 ( s 1 2 n 1 ) 2 + 1 n 2 − 1 ( s 2 2 n 2 ) 2 df=\frac{({{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}})^2}{\frac{1}{n_1-1}(\frac{s^2_1}{n_1})^2+\frac{1}{n_2-1}(\frac{s^2_2}{n_2})^2} df=n1−11(n1s12)2+n2−11(n2s22)2(n1s12+n2s22)2,假设两个总体的标准差相同时:自由度: n 1 + n 2 − 2 n_1+n_2-2 n1+n2−2 - 案例
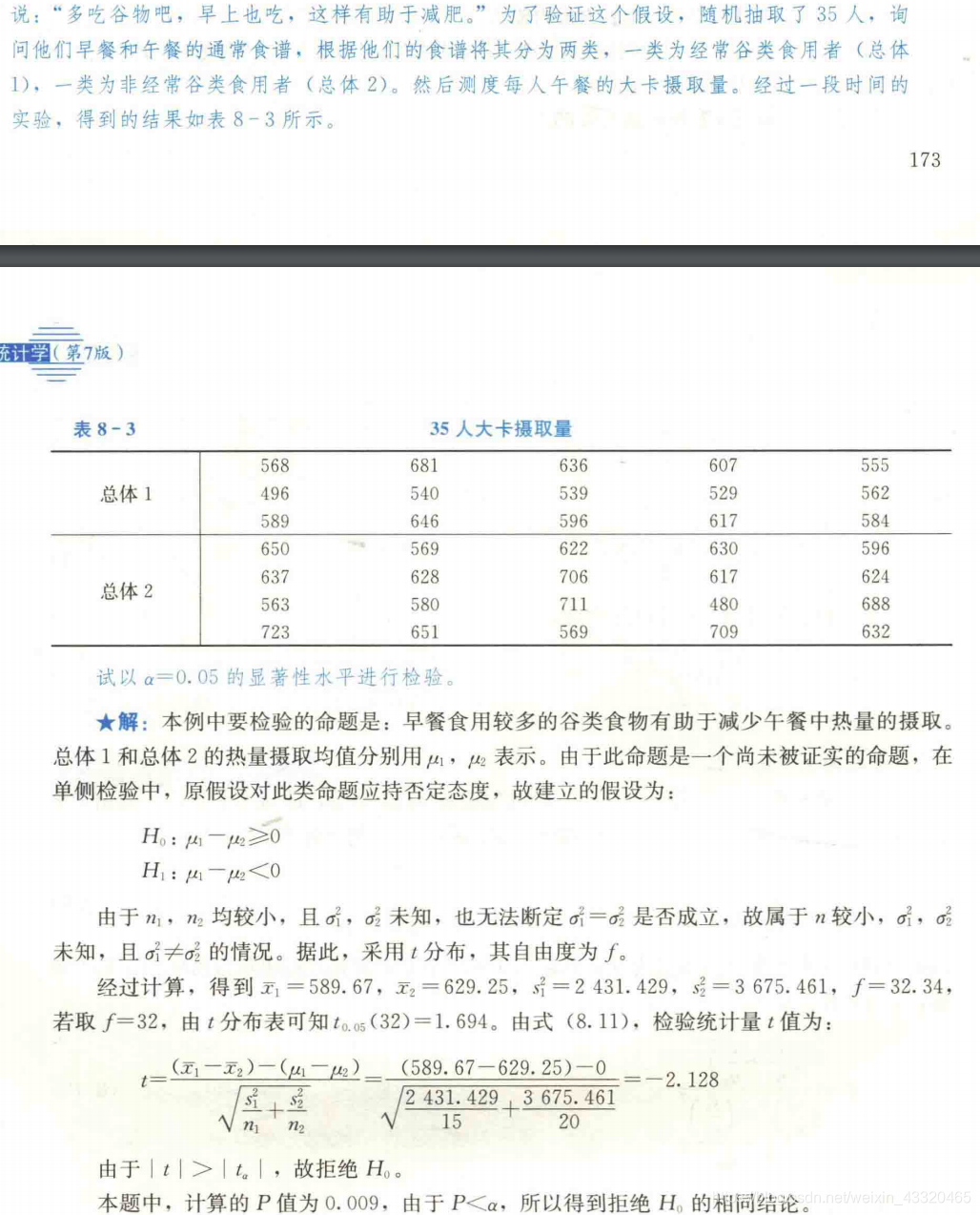
-
均值样本之差 - 匹配样本matched sample)
-
目的:由于匹配样本实质上起到了控制观测变量影响因素的作用,因而可以得到更为精确的推断结果。
- 需要注意的是,在什么情况下可以把两个样本看成是匹配样本?在两个总体参数的检验问题中,根据可能的情况采用匹配样本的设计,可以有效地提高检验的效率。
-
定义:即一个样本中的数据与另个样本中的数据相对应。比如,先指定12个工人用第一种方法组装产品,然后再让这12个工人用第二种方法组装产品,这样得到的两种方法组装产品的数据就是匹配数据。
-
关键:仅考虑差值这一列,假设差值的总体服从正态分布。
-
置信区间
d ‾ ± t α / 2 s d n \overline d \pm t_{\alpha/2}\frac{s_d}{\sqrt{n}} d±tα/2nsd,式中,d表示两个匹配样本对应数据的差值; d ‾ \overline d d表示各差值的均值; σ d \sigma_d σd表示各差值的标准
差。当总体的 σ d \sigma_d σd未知时,可用样本差值的标准差 s d s_d sd来代替
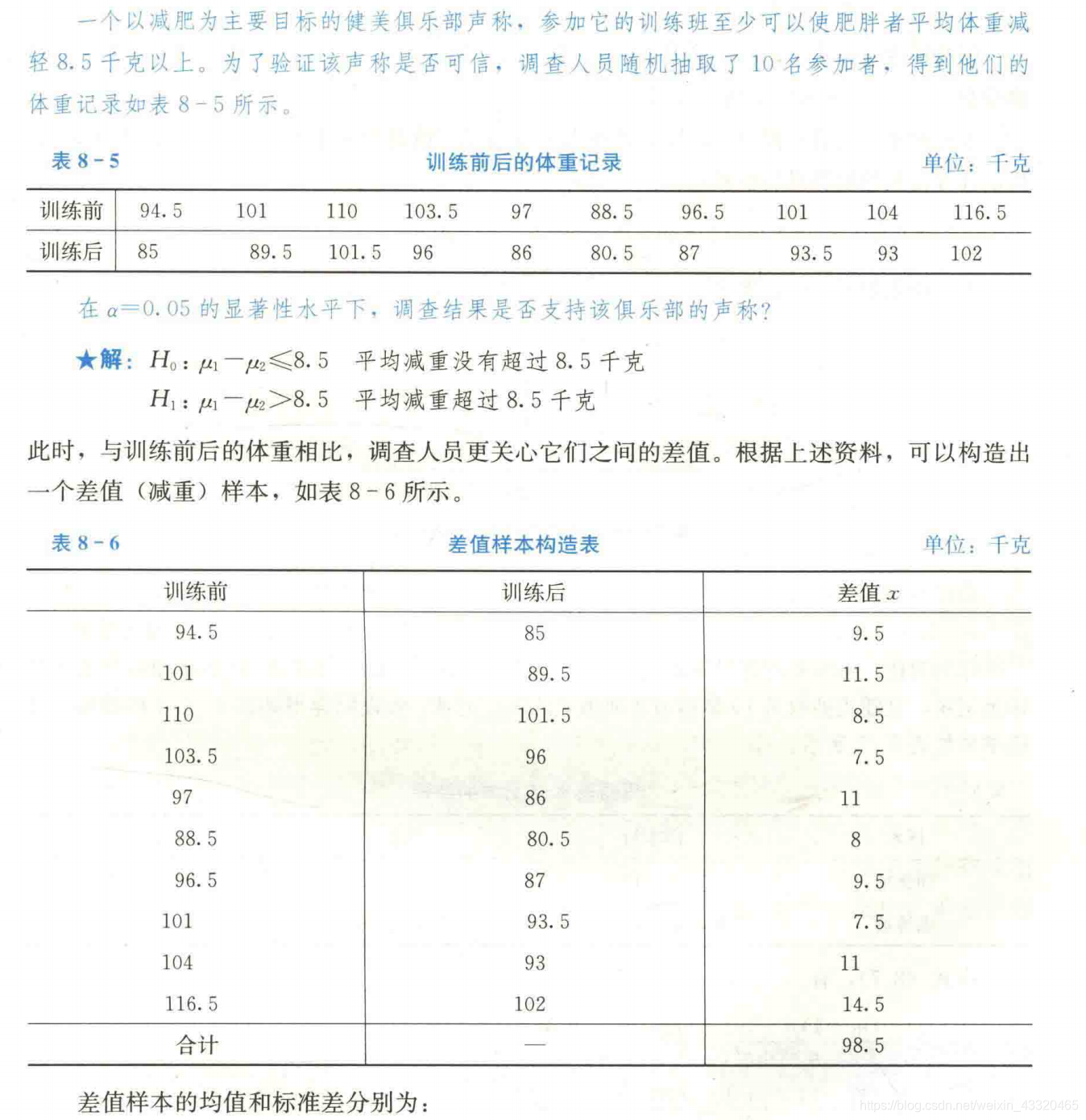
在小样本情况下,假定两个总体各观察值的配对差服从正态分布。两个总体均值之差 μ d = μ 1 − μ 2 \mu_d=\mu_1-\mu_2 μd=μ1−μ2在1-a置信水平下的置信区间为: d ‾ ± t α / 2 ( n − 1 ) s d n \overline d \pm t_{\alpha/2}(n-1)\frac{s_d}{\sqrt{n}} d±tα/2(n−1)nsd- 案例

- 案例
-
检验统计量
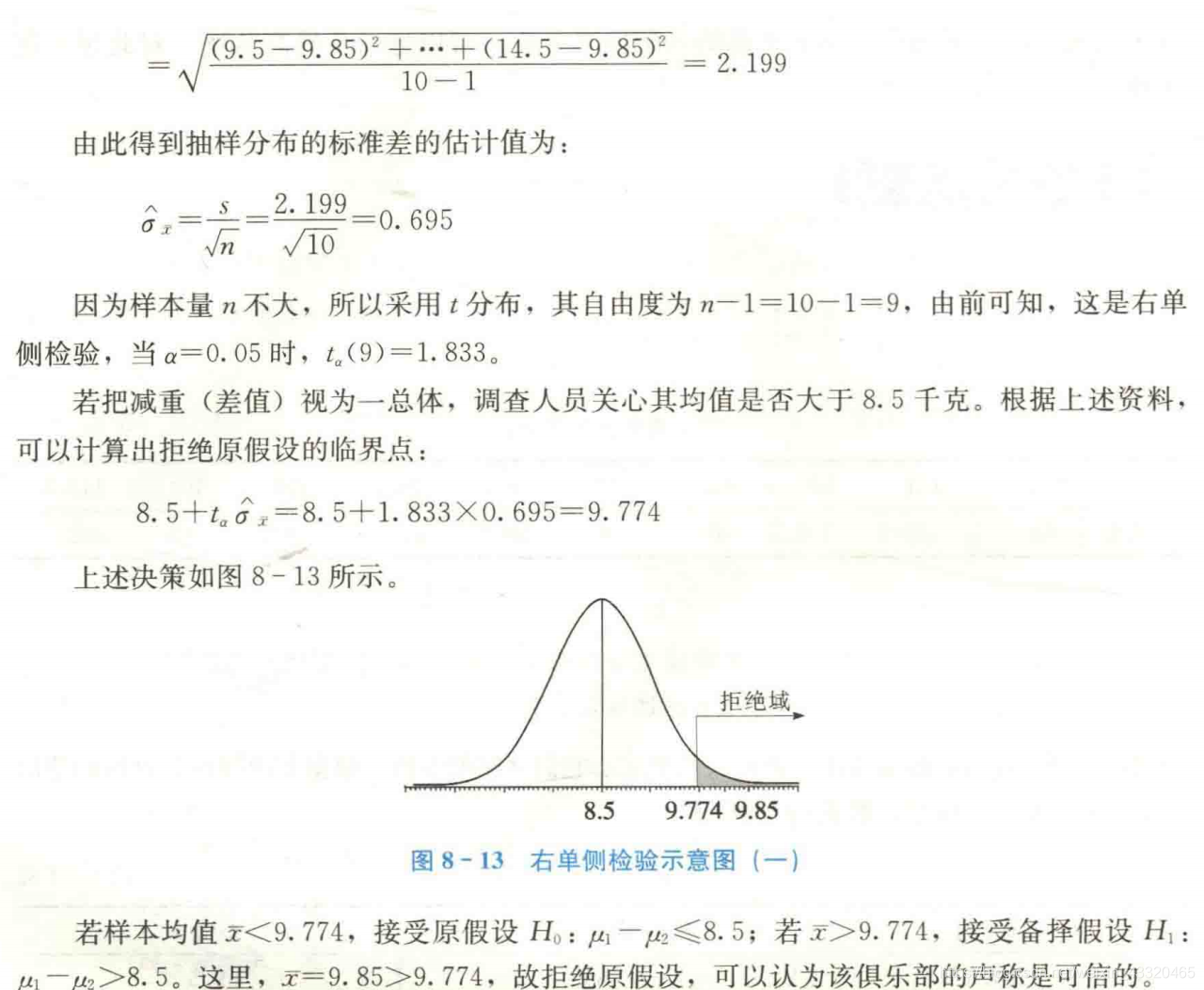
t = d ‾ − μ d s d / n t=\frac{\overline d- \mu _d}{s_d/ \sqrt{n}} t=sd/nd−μd( d ‾ = ∑ d i n \overline d=\frac{\sum d_i}{n} d=n∑di, s d = ∑ ( d i − d ‾ ) 2 n − 1 s_d=\sqrt{\frac{\sum(d_i-\overline d)_2}{n-1}} sd=n−1∑(di−d)2)- 案例

- 案例
-
对比:

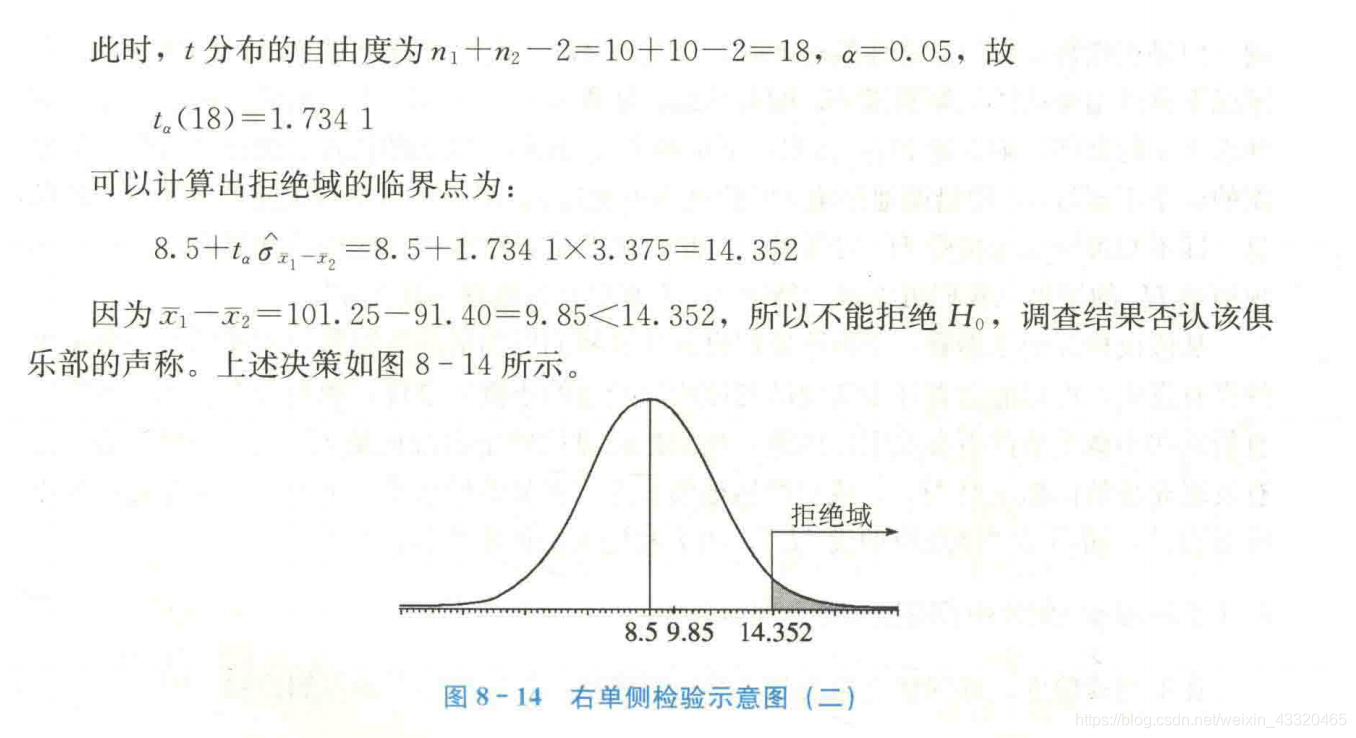
为什么由表8-5中相同的数据会得出不同的结论呢?通过对比可以看出,在匹配样本的检验中,抽样分布的标准差ax=0.695,而在独立样本的检验中,抽样分布的标准差on1-2=3.375。与较小的标准差相比,9.85显著大于8.5;而与较大的标准差相比,9.85大于8.5的程度则不显著。由于匹配样本实质上起到了控制观测变量影响因素的作用,因而可以得到更为精确的推断结果。
比例之差
- 基于
p ‾ 1 − p ‾ 2 \overline p_1-\overline p_2 p1−p2抽样满足正态分布。类似一个总体参数估计中,比例估计,只考虑大样本。能满足四值大于5: n 1 p 1 , n 1 ( 1 − p 1 ) n_1p_1,n_1(1-p_1) n1p1,n1(1−p1), n 2 p 2 , n 2 ( 1 − p 2 ) n_2p_2,n_2(1-p_2) n2p2,n2(1−p2).
由样本比例的抽样分布可知,从两个二项总体中抽出两个独立的样本,则两个样本比例之差的抽样分布服从正态分布。同样,两个样本的比例之差经标准化后服从标准正态分布,即 - 点估计量
- p ‾ 1 − p ‾ 2 \overline p_1-\overline p_2 p1−p2
- 标准误差: σ p ‾ 1 − p ‾ 2 = p ‾ 1 ( 1 − p ‾ 1 ) n 1 + p ‾ 2 ( 1 − p ‾ 2 ) n 2 \sigma_{\overline p_1-\overline p_2}=\sqrt{\frac{\overline p_1(1-\overline p_1)}{n_1}+\frac{\overline p_2(1-\overline p_2)}{n_2}} σp1−p2=n1p1(1−p1)+n2p2(1−p2)
- 区间估计
p ‾ 1 − p ‾ 2 ± z α / 2 p ‾ 1 ( 1 − p ‾ 1 ) n 1 + p ‾ 2 ( 1 − p ‾ 2 ) n 2 \overline p_1-\overline p_2\pm z_{\alpha/2}\sqrt{\frac{\overline p_1(1-\overline p_1)}{n_1}+\frac{\overline p_2(1-\overline p_2)}{n_2}} p1−p2±zα/2n1p1(1−p1)+n2p2(1−p2)

-案例:

- 假设检验
- 形式
- 双侧: H 0 : p = p 0 , H 1 : p ≠ p 0 H_0:p=p_0,H_1:p\neq p_0 H0:p=p0,H1:p=p0
- 单侧:
H 0 : p ≤ p 0 , H 1 : p > p 0 H_0:p\leq p_0,H_1:p>p_0 H0:p≤p0,H1:p>p0; H 0 : p ≥ p 0 , H 1 : p < p 0 H_0:p\geq p_0,H_1:p<p_0 H0:p≥p0,H1:p<p0, - 检验统计量计算:
设两个总体服从二项分布,这两个总体中具有某种特征的单位数的比例分别为x1和
2,但x1和2未知,可以用样本比例p1和p2代替。有以下两种情况: - 1.检验两个总体比例相等的假设
该假设的表达式为: H 0 : π 1 − π 2 = 0 H_0:\pi_1-\pi_2=0 H0:π1−π2=0
P的合并估计点,两个独立样本的点估计加权平均数。在原假设成立的条件下,最佳的方差是p(1-p),其中p是将两个样本合并后得到的比例估计量,即
p = x 1 + x 2 n 1 + n 2 = p 1 n 1 + p 2 n 2 n 1 + n 2 p=\frac{x_1+x_2}{n_1+n_2}=\frac{p_1n_1+p_2n_2}{n_1+n_2} p=n1+n2x1+x2=n1+n2p1n1+p2n2
式中,x1表示样本n1中具有某种特征的单位数;x2表示样本n2中具有某种特征的单位数。
在大样本条件下,统计量z的表达式为:
z = p 1 − p 2 p ( 1 − p ) ( 1 n 1 + 1 n 2 ) z=\frac{p_1-p_2}{\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}} z=p(1−p)(n11+n21)p1−p2
案例:
- 2.检验两个总体比例之差不为零的假设


- 形式
9总体方差的统计推断
前提
χ2(卡方)分布
-
χ2(卡方)分布(chi-square distribution)
- 介绍:
由正态分布构造而成的一个新的分布,当自由度 很大时, 分布近似为正态分布 - 定义:
n个相互独立的随机变量ξ₁,ξ₂,…,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和 Q = ∑ i = 1 n ξ i 2 Q=\displaystyle \sum^{n}_{i=1}{\xi^2_i} Q=i=1∑nξi2构成一新的随机变量,其分布规律称为卡方分布 - 自由度
其中参数 v v v称为自由度,正如正态分布中均数或方差不同就是另一个正态分布一样,自由度不同就是另一个 χ2分布。记为 $Q~ ξ 2 ( v ) \xi^2(v) ξ2(v)或者 (其中 v = n − k v=n-k v=n−k , k为限制条件数)。 - 概率表
- 只能查单侧概率值
查 χ2分布概率表时,按自由度及相应的概率去找到对应的 χ2值,单侧概率χ2 0.05(7)=14.1的查表方法就是,在第一列找到自由度7这一行,在第一行中找到概率0.05这一列,行列的交叉处即是14.1。 - 可以变化一下来查双侧概率值。
例如,要在自由度为7的卡方分布中,得到双侧概率为0.05所对应的上下端点可以这样来考虑:双侧概率指的是在上端和下端各划出概率相等的一部分,两概率之和为给定的概率值,这里是0.05,因此实际上上端点以上的概率为0.05/2=0.025,用概率0.025查表得上端点的值为16,记为 0.05/2(7)=16。下端点以下的概率也为0.025,因此可以用0.975查得下端点为1.69,记为 1-0.05/2(7)=1.69。
- 只能查单侧概率值
- 介绍:
-
样本方差抽样分布(sampling distribution of variance)
从总体中重复随机抽取容量为n的所有样本,其样本方差的概率分布。
当总体服从正态分布,从中抽取容量为n的样本,样本方差与总体方差的比值服从自由度df=n-1的χ2(卡方)分布。- 性质
- 卡方分布密度曲线下的面积都是1.
- 分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),
- 随着参数 v的增大, 分布趋近于正态分布;自由度越小,分布越偏斜。
- 性质
总体方差的统计推断与检验
1. 一个总体
- 置信区间
这里只讨论正态总体方差的估计问题。根据样本方差的抽样分布可知,样本方差服从由度为n-1的χ2分布。因此,用χ2分布构造总体方差的置信区间。
若给定一个显著性水平a,用χ2分布构造的总体方差a的置信区间可用下表示:
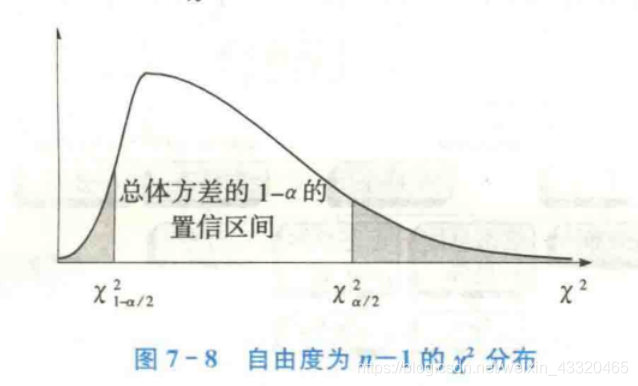
要建立总体方差 σ 2 \sigma^2 σ2的置信区间,也就是要找到一个 χ \chi χ值,使其满足:
χ 1 − α / 2 2 ≤ χ 2 ≤ χ α / 2 2 \chi^2_{1-\alpha/2}\leq\chi^2\leq\chi^2_{\alpha/2} χ1−α/22≤χ2≤χα/22
由于 ( n − 1 ) s 2 σ 2 \frac{(n-1)s^2}{\sigma^2} σ2(n−1)s2~ χ 2 ( n − 1 ) \chi^2(n-1) χ2(n−1),可用它来代替 χ 2 \chi^2 χ2,于是有:
χ 1 − α / 2 2 ≤ ( n − 1 ) s 2 σ 2 ≤ χ α / 2 2 \chi^2_{1-\alpha/2}\leq \frac{(n-1)s^2}{\sigma^2} \leq\chi^2_{\alpha/2} χ1−α/22≤σ2(n−1)s2≤χα/22
根据上式可推导出总体方差 σ 2 \sigma^2 σ2在1- α \alpha α置信水平下的置信区间为:
( n − 1 ) s 2 χ α / 2 2 ≤ σ 2 ≤ ( n − 1 ) s 2 χ 1 − α / 2 2 \frac{(n-1)s^2}{\chi^2_{\alpha/2}}\leq {\sigma^2} \leq\frac{(n-1)s^2}{\chi^2_{1-\alpha/2}} χα/22(n−1)s2≤σ2≤χ1−α/22(n−1)s2- 案例

- 案例
- 假设检验
- 作用:反应稳定性。
方差大,说明产品的性能不稳定,波动大。凡与均值有关的指标,通常也与方差有关,方差从另一个方面说明研究现象的状况。在经济生活方面,对方差关注的例子比
比皆是。例如,居民的平均收入说明了收入达到的一般水平,是衡量经济发展阶段的一个重要指标,而收入的方差则反映了收入分配的差异情况,可以用于评价收入的合理性。在投资方面,收益率的方差是评价投资风险的重要依据。 - 流程:
方差检验的程序,与均值检验、比例检验是一样的,它们之间的主要区别是所使用的检验统计量不同。方差检验所使用的是χ2统计量。
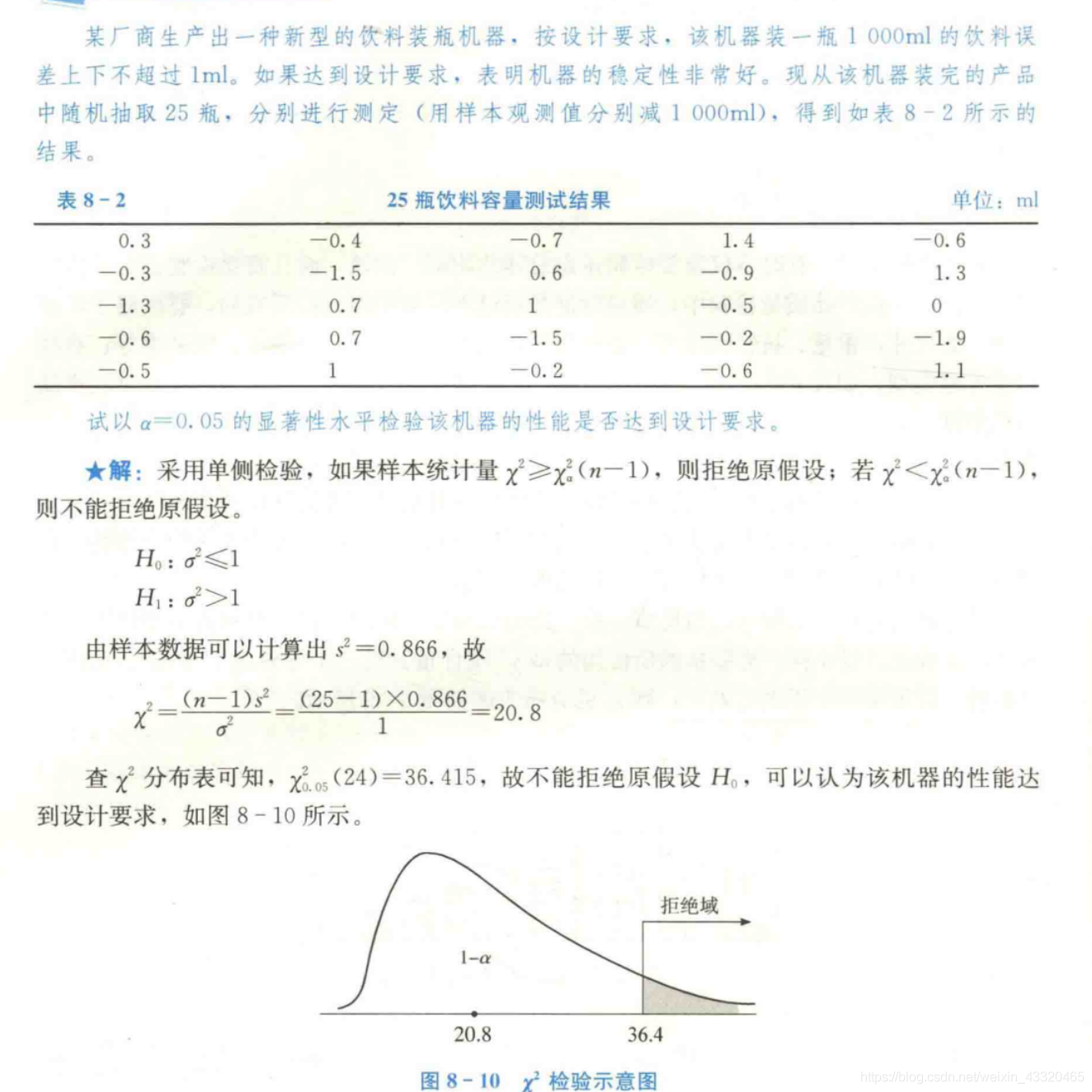
正常情况下χ2是偏态分布,因此常用于单侧检验,临界点在右侧斜尾方向 - 案例:
- 作用:反应稳定性。
2.两个总体
F分布
- F分布
两个服从卡方分布的独立随机变量各除以其自由度后的比值的抽样分布,是一种非对称分布,且位置不可互换。F分布有着广泛的应用,如在方差分析、回归方程的显著性检验中都有着重要的地位。- 统计量
1.若总体X~N(0,1),(X1,X2,Xm)与(Y1,Y2,…,Ymn2)为来自X的两个独立样本,设统计量F
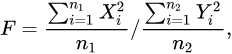
则称统计量F服从自由度n1和n2的F分布,记为F~F(n1,n2)
2.若总体X~ N(μ,1)与总体Y~N(0,1)独立,(X1,X2,…,Xm1)为来自X的一个样本,(Y,Y2,Yn2)为来自Y的
个样本,统计量
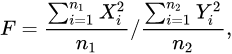
称统计量F服从自由度为n1和n2,非中心参数为 δ = n μ 2 \delta=n\mu^2 δ=nμ2的非中心F分布,记为F~F(n1,n2,δ) - 概率密度曲线
- 统计量
- 置信区间
由于两个样本方差比的抽样分布服从 F ( n 1 − 1 , n 2 − 2 ) F(n_1-1,n_2-2) F(n1−1,n2−2)分布,因此可用F分布来构造两个总体方差比 σ 1 2 / σ 2 2 \sigma^2_1/\sigma^2_2 σ12/σ22的置信区间。用F分布构造的两个总体方差比的置信区间可用图来表示:
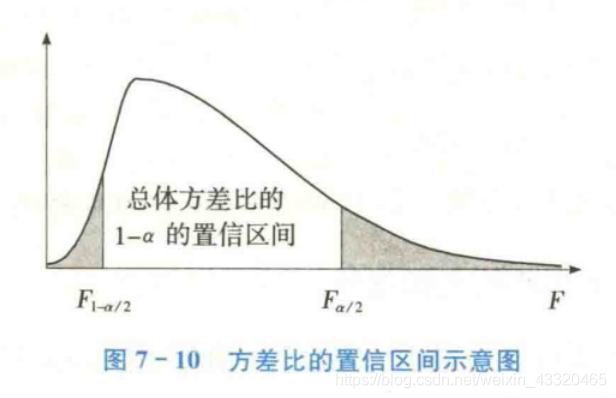
建立两个总体方差比的置信区间,也就是要找到一个F值,使其满足:
F 1 − α / 2 ≤ F ≤ F α / 2 F_{1-\alpha/2}\leq F\leq F_{\alpha/2} F1−α/2≤F≤Fα/2
由于 s 1 2 σ 2 2 s 2 2 σ 1 2 \frac{s_1^2\sigma^2_2}{s_2^2\sigma^2_1} s22σ12s12σ22~ F ( n 1 − 1 , n 2 − 1 ) F(n_1-1,n_2-1) F(n1−1,n2−1),故可用它来代替F,于是有:
F 1 − α / 2 ≤ s 1 2 σ 2 2 s 2 2 σ 1 2 ≤ F α / 2 F_{1-\alpha/2}\leq \frac{s_1^2\sigma^2_2}{s_2^2\sigma^2_1}\leq F_{\alpha/2} F1−α/2≤s22σ12s12σ22≤Fα/2
根据上式可以推导出两个总体方差比 σ 1 2 / σ 2 2 \sigma^2_1/\sigma^2_2 σ12/σ22在1- α \alpha α置信水平下的置信区间为:

式中 F α / 2 F_{\alpha/2} Fα/2和 F 1 − α / 2 F_{1-\alpha/2} F1−α/2是分子自由度为 n 1 − 1 n_1-1 n1−1和分母自由度为 n 2 − 1 n_2-1 n2−1的F分布的右侧面积为 α / 2 和 1 − α / 2 \alpha/2和1-\alpha/2 α/2和1−α/2的分位数。由于F分布表中只给出面积较小的右分位数,此时可利用下面的关系求得F1a/2的分位数值:
F 1 − α / 2 ( n 1 − n 2 ) = 1 F a ( n 2 , n 1 ) F_{1-\alpha/2}(n_1-n_2)=\frac{1}{F_a(n_2,n_1)} F1−α/2(n1−n2)=Fa(n2,n1)1式中,n1表示分子自由度;n2表示分母自由度。
案例:

- 假设检验
-作用
事实上,在许多情况下总体方差是否相等事先往往并不知道,因此在进行两个总体均值之差的检验之前,可以先进行两个总体方差是否相等的检验,由此获得所需要的信息。- 统计量F
F = s 1 2 s 1 2 F=\frac{s_1^2}{s_1^2} F=s12s12
为了比较两个未知的总体方差 σ 1 2 和 σ 2 2 \sigma^2_1和\sigma^2_2 σ12和σ22和,我们用两个样本方差的比来判断,如果F接近1,说明两个总体方差σ和很接近,如果比值远离1,说明a与a之间有较大差异。
在原假设 σ 1 2 = σ 2 2 \sigma^2_1=\sigma^2_2 σ12=σ22下,检验统计量的两个自由度:分子自由度 n 1 − 1 n_1-1 n1−1,分母自由度 n 2 − 1 n_2-1 n2−1。 - 单侧检验中,一般把较大的s2放在分子s的位置,此时F>1,拒绝域在F分布的右侧,原假设和备择假设分别为:H0:a≤02,H1:a1>02,临界点为 F ( n 1 − 1 , n 2 − 1 ) F(n_1-1,n_2-1) F(n1−1,n2−1)。这样处理含义明确,易于理解,而且查表方便。
- 双侧检验
拒绝域在F分布的两侧,两个临界点的位置分别为:
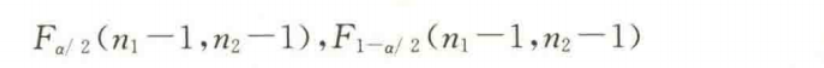

- 统计量F
10多个比率的比较&独立性检验&拟合优度检验
- 目的
根据「样本数据」基于卡方分布检验「多个总体比率」(分类数据的频数进行分析)是否全相等。利用 χ 2 \chi^2 χ2对分类数据进行拟合度检验和独立性检验
1.多个总体比率的相等性检验
-
定义:
- 目的
根据「样本数据」基于卡方分布检验「多个总体比率」(分类数据的频数进行分析)是否全相等。
- 目的
-
假设检验-步骤
- 建立假设
H 0 : p 1 = p 2 = … … p k H_0:p_1=p_2=……p_k H0:p1=p2=……pk
H a , 所 有 比 例 不 全 相 等 H_a,所有比例不全相等 Ha,所有比例不全相等 - 记录「观察频数
f i j f_{ij} fij - 假定「原假设」为真,计算期望频数
e i j = ( R o w − i − T o t a l ) ( R o w − j − T o t a l ) T o t a l S a m p l e S i z e e_{ij}=\frac{(Row-i -Total)(Row-j-Total)}{Total Sample Size} eij=TotalSampleSize(Row−i−Total)(Row−j−Total) - 计算「检验统计量」
条件:每一个单元格的「期望频数」都>=5
计算: χ 2 = ∑ i ∑ j ( f i j − e i j ) 2 e i j \chi^2= \displaystyle \sum_i\displaystyle \sum_j{\frac{(f_{ij}-e_{ij})^2}{e_{ij}}} χ2=i∑j∑eij(fij−eij)2
自由度:k-1
检验显著性水平: α \alpha α - 拒绝法则
if p-value ≤ α \leq \alpha ≤α reject H 0 H_0 H0
if χ 2 ≥ χ α 2 \chi^2\geq \chi_\alpha^2 χ2≥χα2 reject H 0 H_0 H0
- 建立假设
-
多重比较方法
- 应用背景:卡方检验已经证明总体比率「不全」相等。多重比较方法对所有「成对」的「总体比率」○进行统计检验确定○哪些总体比率之间存在差异
- marascuilo检验
(略)
-
多项概率分布
总体的每一个个体被分配到三个或多个类中,一个且仅一个。 -
应用于「两个总体比例相等」的检验
2.独立性检验
- 定义:基于 χ 2 \chi^2 χ2分布,根据样本数据检验,l来自一个总体的「两个分类变量」的「独立性。分析列联表中行变量和列变量是否相互独立。
- 列联表( contingency table)
将两个以上的变量进行交叉分类的频数分布表。例如欲分析原料的质量是否与生产地有关,将500件随机抽取的产品按质量和产地构造列联表。

- 假设检验-步骤
-
建立假设
H 0 : p 1 = p 2 = … … p k H_0:p_1=p_2=……p_k H0:p1=p2=……pk
H a , 所 有 比 例 不 全 相 等 H_a,所有比例不全相等 Ha,所有比例不全相等 -
记录「观察频数
-
假定「原假设」为真,计算期望频数
-
计算「检验统计量」
条件:每一个单元格的「期望频数」都>=5
计算: χ 2 = ∑ i ∑ j ( f i j − e i j ) 2 e i j \chi^2= \displaystyle \sum_i\displaystyle \sum_j{\frac{(f_{ij}-e_{ij})^2}{e_{ij}}} χ2=i∑j∑eij(fij−eij)2
自由度:k-1
检验显著性水平: α \alpha α -
拒绝法则
if p-value ≤ α \leq \alpha ≤α reject H 0 H_0 H0
if χ 2 ≥ χ α 2 \chi^2\geq \chi_\alpha^2 χ2≥χα2 reject H 0 H_0 H0
-
- 案例
一种原料来自三个不同的地区,原料质量被分成三个不同等级。从这批原料中随机抽取500件进行检验,结果如表9-2所示,要求检验各个地区和原料等级之间是否存在依赖关系(a=0.05)。



3.拟合优度检验( goodness of fit test)
- 定义:
基于卡方分布基于卡方分布,依据总体分布状况,计算出分类变量中各类别的期望频数,与分布的观察频数进行对比,判断期望频数与观察频数是否有显著差异,从而达到对分类变量进行分析的目的。 - 多项概率分布
实际是二项概率分布的推广为三个或多个结果,但概率之和仍为1.- 假设检验-步骤
- 建立假设
H 0 : 总 体 服 从 H_0:总体服从 H0:总体服从
H a 总 体 不 服 从 H_a总体不服从 Ha总体不服从 - 记录「观察频数」
f i f_i fi - 假定「原假设」为真,计算期望频数
e i = 样 本 容 量 ∗ 各 类 概 率 e_i=样本容量*各类概率 ei=样本容量∗各类概率 - 计算「检验统计量」
条件:每一个单元格的「期望频数」都>=5
计算: χ 2 = ∑ i = 1 k ( f i − e i ) 2 e i \chi^2= \displaystyle \sum_{i=1}^{k}{\frac{(f_{i}-e_{i})^2}{e_{i}}} χ2=i=1∑kei(fi−ei)2
自由度:k-1
检验显著性水平: α \alpha α - 拒绝法则
if p-value ≤ α \leq \alpha ≤α reject H 0 H_0 H0
if χ 2 ≥ χ α 2 \chi^2\geq \chi_\alpha^2 χ2≥χα2 reject H 0 H_0 H0
- 建立假设
- 案例

- 假设检验-步骤
- 正态分布
由于是连续分布,计算时在多项概率分布的基础上重新修正定义类别的方式和计算期望评述的方法。- 假设检验-步骤
- 建立假设
H 0 : 总 体 服 从 H_0:总体服从 H0:总体服从
H a 总 体 不 服 从 H_a总体不服从 Ha总体不服从 - 抽取一个随机的概率样本。记录「观察频数」
f
i
f_i
fi
计算:样本的均值和标准差。
定义类别:k个取值区间,将连续变量变成分类变量。- 要求:各个区间的期望频数至少为五
- 建议:使用等概率区间方法。
- 计算:样本计算样本n区间数k。计算出Z,结合样本根据样本均值和样本标准差计算出个区间的取值。
- 记录:每个区间对应的观察频数 f i f_i fi。
- 假定「原假设」为真,计算期望频数
e i = 样 本 容 量 ∗ 侦 探 分 布 落 入 各 个 区 间 的 概 率 e_i=样本容量*侦探分布落入各个区间的概率 ei=样本容量∗侦探分布落入各个区间的概率 - 计算「检验统计量」
条件:每一个单元格的「期望频数」都>=5
计算: χ 2 = ∑ i = 1 k ( f i − e i ) 2 e i \chi^2= \displaystyle \sum_{i=1}^{k}{\frac{(f_{i}-e_{i})^2}{e_{i}}} χ2=i=1∑kei(fi−ei)2
自由度:k-1-p(由样本估计分布参数个由样本估计分布参数个数决定,例如上述由样本估计分布参数个数决定。例如上述采用和标准差。所以p=2
检验显著性水平: α \alpha α - 拒绝法则
if p-value ≤ α \leq \alpha ≤α reject H 0 H_0 H0
if χ 2 ≥ χ α 2 \chi^2\geq \chi_\alpha^2 χ2≥χα2 reject H 0 H_0 H0
- 建立假设
- 假设检验-步骤
11实验设计&方差分析
基础介绍
-
统计研究分类
-
实验性数据
- 数据获取方法:控制实验变量,收集应变量
- 实验设计方法:
完全随机化设计:「处理」被随机的指派给「实验单元」的一种「实验设计
随机化区组设计○使用「区组划分」的一种实验设计
析因实验允许得到有关「两个或两个以上因子」同时存在的结论 - 很容易验证 因果关系
-
观察性数据
- 数据获取方法 :抽样调查
- 很难验证:因果关系
-
-
基础概念
-
因子factor:
要检验的对象,即引起关注的「自变量」- 处理:因子的不同表现,
- 观测值:在每个因子水平下得到的样本数据。
- 单因子实验:只涉及「一个因子」的实验.包含分类型自变量和数据型因变量。
- 例如:总体中抽取的样本数据。再如,要在不同的温度下进行一项试验,温度就是一个因素,20℃,25℃,30℃,35℃4个温度值下做试验,每个温度值就是一个水平(分类型自变量),共有4个水平,在每个温度下试验得到的数据就是观测值(数据型因变量)。
- 组内误差:来自同一(总体)水平下的内的数据误差,可以看做随机因素造成的随机误。20℃内个数据的误差
- 组间误差:由随机误差和系统误差组成。即有抽样本身形成的随机误差 和不同总体的系统性因素造成的误差
- SST
反映全部数据误差大小的平方和称为总平方和,记为SST。例如,所抽取的全部23家企业被投诉次数之间的误差平方和就是总平方和,它反映了全部观测值的离散状况.

- SSE
反映组内误差大小的平方和称为组内平方和,也称为误差平方和或残差平方和,记为SSE。例如,每个样本内部的数据平方和加在一起就是组内平方和,它反映了每个样本内各观测值的离散状况。 - SSA
反映组间误差大小的平方和称为组间平方和,也称为因素平方和,记为SSA。例如,四个行业被投诉次数之间的误差平方和就是组间平方和,它反映了样本均值之间的差异 - 误差分析
通过组间误差与组内误差经过平均后数值比值(称为均方或方差)接近程度。接近1组间误差中只包含随机误差,而没有系统误差。当这个比值大到某种程度时,就认为因素的不同水平之间存在着显著差异,也就是自变量对因变量有显著影响。 - 响应变量:即引起关注的「应变量」
- 实验单元:实验中引起关注的「研究对象
- 随机化:将「处理」随机的指派给「实验单元」的过程
- 分解:将「总平方和」与「自由度」分配给「各组成部分」的过程
-
本篇「统计检验」的基础
建立在总体方差的两个独立估计量上,
方差分析ANOVA
- 定义
表面上看,方差分析是检验多个总体均值是否相等的统计方法,但本质上它所研究的是分类型自变量对数值型因变量的影响,例如,变量之间有没有关系,关系的强度如何等。
方差分析( analysis of variance, ANOVA)就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。 - 优点
与假设检验方法相比,方差分析不仅可以提高检验的效率,同时由于它将所有的样本信息结合在一起,排除了错误累积的概率,从而避免拒绝一个真实的原假设,因此增加了分析的可靠性。 - 假定条件
(1)每个总体都应服从正态分布
(2)各个总体的方差必须相同。也就是说,各组观察数据是从具有相同方差的正态总体中抽取的。例如,在例10.1中,要求每个行业被投诉次数的方差都相同。
(3)观测值是独立的。例如,在例10.1中,要求每个被抽中的企业被投诉次数都与其他企业被投诉次数独立。 - 问题的一般提法
设因素有k个水平,每个水平的均值分别用A,p,…,表示,要检验k个水平(总体)的均值是否相等,需要提出如下假设:
H 0 : μ 1 = μ 2 = … = μ k H_0:μ_1=μ_2=…=μ_k H0:μ1=μ2=…=μk:自变量对因变量没有显著影响
H 1 : μ , μ 2 , … , μ k H_1:μ_,μ_2,…,μ_k H1:μ,μ2,…,μk:不全相等自变量对因变量有显著影响
(本章至此跳过,需要时再来补充)
完全随机化实验设计
多重比较方法
随机化区间组设计
分析实验
12简单线性回归
- 假定ⅹ和y之间关系的回归模型
- 利用最小二乘法,建立估计的回归方程
- 判定系数,表明估计的回归方程,是对样本数据较好的拟合
- 假设检验,判断X,y之间,是否存在一个显著的回归关系
- 利用残差分析,证实回归模型的假定,否成立
- 利用估计的回归方程,进行估计和预测
1.回归模型
- 概念
- 自变量:用于「预测或解释」用x表示
- 应变量:被预测或被解释的变量 y
- 回归模型 描述y如何依赖于x ,误差e
- 回归方程:描述y的期望值E(y)如何依赖x的方程
- 估计的回归方程:根据样本数据,利用最小二乘法,建立回归方程的估计
- 注意:回归分析不能说明因果关系,只能表示以怎样的程度联系在一起
- 简单线性回归
- 简单线性回归估计步骤

- 定义:含有自变量和因变量。两个变量之间的关系含有自变量和因变量。两个变量之间的关系用一条直线来
- 简单线性回归模型:
y
=
β
0
+
β
1
x
+
ϵ
y=\beta_0+\beta_1x+\epsilon
y=β0+β1x+ϵ
( β 0 \beta_0 β0:截距 , β 1 \beta_1 β1:斜率, ϵ \epsilon ϵ:模型误差估计,本质上是随机变量,说明了包含在y中但是不能被x和y之间的线性光解释的变异性) - 简单线性回归方程:
y = β 0 + β 1 x y=\beta_0+\beta_1x y=β0+β1x ,强调对于x的给一个给定值。回归方程得出y的平均值。 - 估计的简单线性回归方程
y ^ = b 0 + b 1 x \hat{y}=b_0+b_1x y^=b0+b1x
( b 0 b_0 b0 b 1 b_1 b1 给出了 β 0 \beta_0 β0 , β 1 \beta_1 β1的估计值, y ^ : Y 的 平 均 值 E ( y ) 的 一 个 估 计 点 \hat{y}:Y的平均值E(y)的一个估计点 y^:Y的平均值E(y)的一个估计点)
- 简单线性回归估计步骤
最小二乘法
- 目的:利用「样本数据」建立「估计的回归方程」。通过使因变量的观测值
y
i
y_i
yi与估计值
y
^
i
\hat y_i
y^i之间的离差平方和达达到最小来估计
β
1
\beta_1
β1和
β
0
\beta_0
β0

- 准则: m i n ∑ ( y i − y ^ i ) 2 min\sum{(y_i-\hat y_i)}^2 min∑(yi−y^i)2, y i y_i yi:观测值, y ^ i \hat y_i y^i预测值。
- 结果:估计的斜率和截距
b 1 = ∑ ( x i − x ‾ ) ( y i − y ‾ ) ∑ ( x i − x ‾ ) 2 b_1=\frac{\sum(x_i-\overline x)(y_i-\overline y)}{\sum(x_i-\overline x)^2} b1=∑(xi−x)2∑(xi−x)(yi−y), b 0 = y ‾ − b 1 x ‾ b_0=\overline y-b_1\overline x b0=y−b1x
2.判定系数
-
目的
用来度量「估计的回归方程」的「拟合优度」应变量y的「变异性」能被「估计的回归方程」解释的部分③所占的比例 -
概念
- 残差:「观测值」和「预测值」之间的「离差」, y i − y ^ i y_i-\hat y_i yi−y^i
- 总的平方和SST
观测值在直线 y ‾ \overline y y周围的聚集程度。n次观察的总离差, S S T = ∑ ( y i − y ^ i ) 2 SST= \sum(y_i-\hat y_i)^2 SST=∑(yi−y^i)2
S S T = S S R + S S E SST=SSR+SSE SST=SSR+SSE
每个观测点的离差:

- 误差平方和
除线性变化之外的影响,误差平方, S S E = ∑ ( y i − y ^ i ) 2 SSE=\sum(y_i-\hat y_i)^2 SSE=∑(yi−y^i)2 - 回归平方和SSR
观测值在回归线周围的聚集程度,线性变化带来的影, S S T = ∑ ( y ^ i − y i ) 2 SST= \sum(\hat y_i -y_i)^2 SST=∑(y^i−yi)2
-
★判定系数 R 2 R^2 R2
- 对估计的回归方程拟合优度的度量。
- 计算公式: r 2 = S S R S S T r^2=\frac{SSR}{SST} r2=SSTSSR
- 推理:越拟合,SSE越接近0, r 2 r^2 r2越接近1.总的平方和中能被(SSR)解释的百分比
- 案例

-
相关系数
r x y = ( s i g n o f b 1 ) r 2 r_{xy}=(sign of b_1)\sqrt{r^2} rxy=(signofb1)r2 -
判定系数vs相关系数
- 判定系数
范围:0-1、适用于多个变量和非线性关系 - 相关系数
范围:-1-1,只适用于两个变量和线性关系
- 判定系数
3.模型假定
- 为什么要假定模型
r 2 r^2 r2较大,仅能得出拟合较好;不能得出X,y之间的关系是否显著
应用「估计回归方程」前先要判断「假定模型」的合理性即⊙检验「变量之间关系」的显著性,★首先需要满足⊙「误差项」的假定 - 误差项的假定
- 关于回归模型
根据样本数据拟合回归方程时,实际上已经假定变量x与y之间存在着线性关系,即 y = β 0 + β 1 x + ϵ , y=\beta_0+\beta_1x+\epsilon, y=β0+β1x+ϵ,并假定误差项 ϵ \epsilon ϵ是一个服从正态分布的随机变量,且对不同的x具有相同方差。但这些假设是否成立,需要通过检验来证实。
回归分析中的显著性检验主要包括两方面内容:一是线性关系的检验;二是回归系数
的检验。 - ∈的假定
- 平均值/期望值为0
表明 β 0 , β 1 \beta_0 ,\beta_1 β0,β1都是常数, E ( β 0 , β 1 ) = β 0 , β 1 E(\beta_0 ,\beta_1)= \beta_0 ,\beta_1 E(β0,β1)=β0,β1,对于给定的x,对于给定的时候,y的期望值: E ( y ) = β 0 + β 1 x E(y)=\beta_0 +\beta_1x E(y)=β0+β1x - 对于所有的x值
∈的方差均相同,记为 σ 2 \sigma^2 σ2
y关于「回归直线」的方差等于 σ 2 \sigma^2 σ2
对于所有x值,y的方差均相等 - ∈的值是「相互独立」的
对于「特定」的x值,对应的「ε值」与「其他ⅹ值」对应的ε值「不相关」;「对应的y值」与「其他ⅹ值」对应的y值「不相关」 - ∈是一个「正态分布」的随机变量
因为y是∈的一个线性函数,y也是一个「正态分布」的随机变量
- 平均值/期望值为0
- 总结(结合下图)
从图11-6可以看出,E(y)的值随着x的不同而变化,但无论x怎样变化,ε和y的概率分布都是正态分布,并且具有相同的方差。

- 关于回归模型
4.显著性检验
-
解释
根据样本数据拟合回归方程时,实际上已经假定变量x与y之间存在着线性关系,即 y = β 0 + β 1 x + ϵ , y=\beta_0+\beta_1x+\epsilon, y=β0+β1x+ϵ,并假定误差项 ϵ \epsilon ϵ是一个服从正态分布的随机变量,且对不同的x具有相同方差。回归分析中的显著性检验主要包括两方面内容:一是线性关系的检验;二是回归系数 -
目的:
判定判 β 1 \beta_1 β1一的值是否为零
检验两变量之间是否存在一个显著的回归关系。 -
1.线性关系的检验,F-Test
- 检验的统计量,MSR/MSE.
- MSR
称为均方回归,将SSR除以其相应的自由度.(SSR的自由度是自变量的个数k,一元线性回归中自由度为1,SSR/1)的结果 - MSE
称为均方残差,将SSE除以其相应的自由度.(SSE的自由度为n-k-1,一元线性回归中自由度为n-2,SSE/(n-2))的结果
- MSR
- 步骤
- 第1步:提出假设。
H 0 : β 1 = 0 H_0:\beta_1 =0 H0:β1=0 两个变量之间的线性关系不显著 - 第2步:计算检验统计量F
F= MSR/MSE. - 第3步:作出决策。确定显著性水平α,并根据分子自由度df1=1和分母自由度df2=n-2查F分布表,找到相应的临界值 F a F_a Fa。若F> F a F_a Fa。,拒绝H_0。,表明两个变量之间的线性关系是显著的;若F< F a F_a Fa,不拒绝H,没有证据表明两个变量之间的线性关系显著。
- 第1步:提出假设。
- 检验的统计量,MSR/MSE.
-
2.回归系数的检验 T-TEST
- 目的:回归系数的显著性检验是要检验自变量对因变量的影响是否显著:检验回归系数 β 1 \beta_1 β1是否等于0。
- 统计量:t, β 1 \beta_1 β1根据最小二乘法得到的( β 1 = t α / 2 S b 1 ) \beta_1=t_{\alpha/2}S_{b_1}) β1=tα/2Sb1), t = β ^ 1 − β 1 s β 1 ^ t=\frac{\hat{\beta}_1-\beta_1}{s\hat{\beta_1}} t=sβ1^β^1−β1,( β ^ 1 \hat\beta_1 β^1服从正态分布,统计量服从自由度为n-2的t分布),
- 步骤
- 第1步:提出检验
H 0 : β 1 = 0 ; H 1 : β 1 ≠ 0 H_0:\beta_1=0;H_1:\beta_1≠0 H0:β1=0;H1:β1=0 - 第2步:计算检验统计量t
t = β ^ 1 − β 1 s β 1 ^ t=\frac{\hat{\beta}_1-\beta_1}{s\hat{\beta_1}} t=sβ1^β^1−β1 - 第3步:作出决策。
确定显著性水平α,并根据自由度 d f = n − 2 df=n-2 df=n−2查t分布表,找到相应的临界值 t α / 2 t_{\alpha/2} tα/2。
若|t|> t α / 2 t_{\alpha/2} tα/2,则拒绝 H 0 H_0 H0.回归系数等于0的可能性小于a,表明自变量x对因变量y的影响是显著的,换言之,两个变量之间存在着显著的线性关系;
若|t|< t α / 2 t_{\alpha/2} tα/2,则拒绝 H 0 H_0 H0则不拒绝H。,没有证据表明x对y的影响显著,或者说,二者之间尚不存在显著的线性关系。
- 第1步:提出检验
-
总结
在一元线性回归中,自变量只有一个,上面介绍的F检验和t检验是等价的;也就是说,如果H:B=0被t检验拒绝,它也将被F检验拒绝。但在多元回归分析中,这两种检验的意义是不同的。F检验只是用来检验总体回归关系的显著性,而t检验则是检验各个回归系数的显著性。 -
注意
- 显著性检验只能说明两变量之间有显著关系,不能说明线性关系和因果关系。
- F-test、t-test 统计量检验是基于误差项 ϵ \epsilon ϵ的正态性,检验正态性的简单方法是画出残差的直方图或正态概率图。
- 相关系数的检验与F-test、t-test 结果相同
5.估计回归方程的应用
-
预测
所谓预测( predict)是指通过自变量x的取值来预测因变量y的取值。回归模型经过各种检验并证实符合预定的要求后,就可以利用它来预测因变量了。 -
点估计
利用估计的回归方程,对于x的一个特定值 x 0 x_0 x0,求出y的一个估计值就是点估计。点估计可分为两种:一是平均值的点估计;二是个别值的点估计。- 平均值的点估计
利用估计的回归方程,对于x的一个特定值 x 0 x_0 x0,求出y的平均值的一个估计值 E ( y 0 ) E(y_0) E(y0)。 - 个别值的点估计
利用估计的回归方程,对于x的一个特定值x0,求出y的一个个别值的估计值y。
- 平均值的点估计
-
区间估计
利用估计的回归方程,对于x的一个特定值 x 0 x_0 x0,求出y的一个估计值的区间就是区间估计。区间估计也有两种类型:一是置信区间估计(更精确),二是预测区间估计

- 置信区间
它是对x的一个给定值 x 0 x_0 x0,求出y的平均值的估计区间,这一区间称为置信区间( confidence interval);- 计算

- 案例 :

- 计算
- 预测区间估计
它是对x的一个给定值x0,求出y的一个个别值的估计区间,这一区间称为预测区间(prediction interval)- 计算

- 案例

- 计算
- 置信区间
6.残差分析
-
简介
残差分析( residual analysis),确定有关 ϵ \epsilon ϵ的假定是否成立的方法之一.
在回归模型y=A+B1x+ε中,假定ε是期望值为0、方差相等且服从正态分布的一随机变量。如果关于ε的假定不成立,那么,所做的检验以及估计和预测也站不住脚. -
残差与残差图
- 残差( residua)
因变量的观测值y;与根据估计的回归方程求出的预测值 y ^ i \hat{y}_i y^i;之差,用e表示。它反映了用估计的回归方程去预测 y i y_i yi而引起的误差。
第i个观测值的残差可以写为: e i = y i − y ^ i e_i=y_i-\hat{y}_i ei=yi−y^i - 残差图
对假定「随机误差项」「方差相同」的验证 - 图
x轴自变量
y轴残差 : e i = y i − y ^ i e_i=y_i-\hat{y}_i ei=yi−y^i - 解读
如果假定对于所有x值,∈的方差是相同的,所有散点都应落在一条水平带中间。

- 残差( residua)
-
标准化残差
标准化残差( standardized residual)是残差除以它的标准差后得到的数值,也称为 Pearson残差或半学生化残差( semi-studentized residuals),用 z e z_e ze表示。
第i个观测值的标准化残差可以表示为:
z e i = e i s e = y i − y ^ i s e z_{e_i}=\frac{e_i}{s_e}=\frac{y_i-\hat{y}_i}{s_e} zei=seei=seyi−y^i, s e s_e se是残差的标准差的估计。- 标准化残差图
x-标准化残差

- 标准化残差图
-
正态概率草图
- 目的
用「正态分数」去确定 标准化残差 服从「标准正态概率分布」 - 残差图
x轴:正态分数- 正态分数
- 其他
略
- 目的
-
检测
- 异常值
- 定义
与其余的数据点所显示的趋势不符合的数据点 - 方法
散点图、标准化残差图 - 原理
异常值○用来检测○一种标准化残差
1.从数据集删除,第ⅰ次观测值
2.利用,其余的n-1次观测值,建立新的估计回归方程
3.计算,新(修正)的估计的标准误差 S ( i ) S_{(i)} S(i)
4.判断:如果 S ( i ) S_{(i)} S(i)<s第i次观测值为异常值
- 定义
- 有影响的观测值
- 定义
对回归的结果有强影响的观测值 - 包括
异常值:大的残差
极端值:高杠杆率点,高杠杆率(自变量的 - 杠杆率
定义:反映自变量数值与平均值之间差距的度量
杠杆率临界值:经验法则, h i > 3 ( p + 1 ) / n h_i>3(p+1)/n hi>3(p+1)/n - 库克距离测量
定义:建立在第i次观测的杠杆率,第i次观测残差
度量:观测影响程度
公式:p:自变量的个数;s:估计的标准误差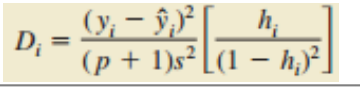
经验法则:第i次观测值是一个有影响的观测值
的基础上
- 定义
- 异常值
13多元回归
- 多元回归
在许多实际问题中,影响因变量的因素往往有多个,这种一个因变量与多个自变量的回归问题就是多元回归, - 多元线性回归
当因变量与各自变量之间为线性关系时,称为多元线性回归。
多元线性回归分析的原理同一元线性回归基本相同,但计算上要复杂得多,需借助计算机来完成。
模型基础
- 多元回归模型
y = β 0 + β 1 x 1 + β 2 x 2 + … + β p x p + ϵ y=\beta_0+\beta_1x_1+\beta_2x_2+…+\beta_px_p+\epsilon y=β0+β1x1+β2x2+…+βpxp+ϵ
描述y是如何依赖,自变量和误差项的数学方程。
误差项,包含在y里面但不能被p个自变量的线性关系解释的变异性 - 多元回归方程
E ( y ) = β 0 + β 1 x 1 + β 2 x 2 + … + β p x p E(y)=\beta_0+\beta_1x_1+\beta_2x_2+…+\beta_px_p E(y)=β0+β1x1+β2x2+…+βpxp
应变量y的「期望值」与自变量的值○之间关系的数学方程 - 估计的多元回归方程
y = b 0 + b 1 x 1 + b 2 x 2 + … + b p x p y=b_0+b_1x_1+b_2x_2+…+b_px_p y=b0+b1x1+b2x2+…+bpxp
b是β的估计值
求解:最小二乘法
拟合度优化
- 多重判定系数( multiple coefficient of determination)
多元回归中的回归平方和总平方和的比例,它是度量多元回归方程拟合程度的一个统计量,反映了因变量y的变中被估计的回归方程所解释的比例。
R 2 = S S R / S S T R^2=SSR/SST R2=SSR/SST
SST=SSR+SSE- 修正多重判定系数
- 方法:用自变量个数进行调整。
- 理由:增加「自变量」将影响估计回归方程解释的百分比, R 2 R^2 R2会变大
- 目的:避免过高估计由于自变量数目增加而带来的影响
- 公式: R a 2 = 1 − ( 1 − R 2 ) n − 1 n − p − 1 R^2_a=1-(1-R^2)\frac{n-1}{n-p-1} Ra2=1−(1−R2)n−p−1n−1(n观测值的数目,p自变量的数目)
- 注意: R 2 R^2 R2值较小,自变量数目较多
- 修正多重判定系数
模型的假定
- ∈的假定
- 平均值/期望值为0
表明 β 0 , β 1 \beta_0 ,\beta_1 β0,β1都是常数, E ( β 0 , β 1 ) = β 0 , β 1 E(\beta_0 ,\beta_1)= \beta_0 ,\beta_1 E(β0,β1)=β0,β1,对于给定的x,对于给定的时候,y的期望值: E ( y ) = E(y)= E(y)=\beta_0 +\beta_1x$ - 对于所有的x值∈的方差均相同,记为
σ
2
\sigma^2
σ2
y关于「回归直线」的方差等于 σ 2 \sigma^2 σ2
对于所有x值,y的方差均相等 - ∈的值是「相互独立」的
对于「特定」的x值,对应的「ε值」与「其他ⅹ值」对应的ε值「不相关」;「对应的y值」与「其他ⅹ值」对应的y值「不相关」 - ∈是一个「正态分布」的随机变量
因为y是∈的一个线性函数,y也是一个「正态分布」的随机变量
- 总结(结合下图)
从图11-6可以看出,E(y)的值随着x的不同而变化,但无论x怎样变化,ε和y的概率分布都是正态分布,并且具有相同的方差。

显著性检验
-
对比
- 简单线性回归,t检验和F检验,目的与结论相同
- 多元回归
F-test :总体的显著性检验;目的:应变量和所有自变量之间否存在显著性关系
t-test:单独显著性检验;目的:f检验已经表明「模型总体」的显著性,t检验用于确定每一个「单个的自变量」是否显著即应变量和单个自变量之间是否存在显著关系
-
1.总体显著性的检验,F-Test
- 检验的统计量,F=MSR/MSE.
- MSR
称为均方回归,将SSR除以其相应的自由度.(SSR的自由度是自变量的个数p)的结果。 - MSE
称为均方残差,将SSE除以其相应的自由度.(SSE的自由度为n-p-1)的结果
- MSR
- 步骤
- 第1步:提出假设。
H 0 : β 1 = β 2 = β 3 … … β k = 0 H_0:\beta_1=\beta_2=\beta_3……\beta_k =0 H0:β1=β2=β3……βk=0
H 1 : β 1 , β 2 , β 3 … … β k 至 少 有 一 个 不 为 0 H_1:\beta_1,\beta_2,\beta_3……\beta_k 至少有一个不为0 H1:β1,β2,β3……βk至少有一个不为0 - 第2步:计算检验统计量F
F= MSR/MSE. - 第3步:作出决策。确定显著性水平α,并根据分子自由度df1=k和分母自由度df2=n-k-1查F分布表,找到相应的临界值 F a F_a Fa。若F> F a F_a Fa,拒绝H_0,表明两个变量之间的线性关系是显著的;若F< F a F_a Fa,不拒绝H,没有证据表明两个变量之间的线性关系显著。根据计算机输出的结果,可直接利用P值作出决策:若P<α,则拒绝原假设;若P>α,则不拒绝原假设
- 第1步:提出假设。
- 检验的统计量,F=MSR/MSE.
-
2.单个参数显著性的 T-TEST
- 目的:回归方程通过线性关系检验后,就可以对各个回归系数 β i \beta_i βi有选择地进行一次或多次检验。但究竟要对哪几个回归系数进行检验,通常需要在建立模型之前作出决定,此外,还应对回归系数检验的个数进行限制,以避免犯过多的第Ⅰ类错误
- 步骤
-
第1步:提出检验
H 0 : β i = 0 ; H 1 : β 1 ≠ 0 H_0:\beta_i=0;H_1:\beta_1≠0 H0:βi=0;H1:β1=0 -
第2步:计算检验统计量t
t = β ^ i s β i ^ t=\frac{\hat{\beta}_i}{s\hat{\beta_i}} t=sβi^β^i~ t ( n − k − 1 ) t(n-k-1) t(n−k−1)
S β ^ i S_{\hat{\beta}_i} Sβ^i是回归系数 β ^ i {\hat{\beta}_i} β^i的抽样分布的标准差: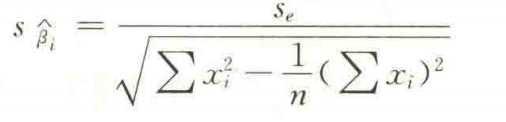
-
第3步:作出决策。
确定显著性水平α,并根据自由度 d f = n − k − 1 df=n-k-1 df=n−k−1查t分布表,找到相应的临界值 t α / 2 t_{\alpha/2} tα/2。
若|t|> t α / 2 t_{\alpha/2} tα/2,则拒绝 H 0 H_0 H0
若|t|< t α / 2 t_{\alpha/2} tα/2,则拒绝 H 0 H_0 H0则不拒绝H
-
多重共线性
-
定义:自变量之间的相关性
-
问题: 自变量之间不一定是独立,自变量高度相关时,对回归系数的解释是危险的。可能对模型估计产生问题:
- 任一自变量对应变量的单独影响无法确定,即:F检验,显著;单独参数t检验却不显著。相关性叠加
- 对参数估计的正负产生影响,特别是 β i d \beta_id βid的正负号可能与预期性相反。
- 对于两个自变量情形,样本相关系数绝对值大于0.7,可能产生多重共线性潜在影响
-
检测
检测多重共线性的方法有多种,其中最简单的一种办法是计算模型中各对自变量之间的相关系数,并对各相关系数进行显著性检验。
如果有一个或多个相关系数是显著的,就表示模型中所使用的自变量之间相关,因而存在多重共线性问题。具体来说,如果出现下列情况,则暗示存在多重共线性:
(1)模型中各对自变量之间显著相关
(2)当模型的线性关系检验(F检验)显著时,几乎所有回归系数β的t检验却不
显著。
(3)回归系数的正负号与预期的相反。
(4)容忍度( tolerance)与方差扩大因子( variance inflation factor,VIF)。某个自变量的容忍度等于1减去该自变量为因变量而其他k-1个自变量为预测变量时所得到的线性回归模型的判定系数,即1-R。容忍度越小,多重共线性越严重。通常认为容忍度小于0.1时,存在严重的多重共线性。方差扩大因子等于容忍度的倒数,即N1-R°显然,VIF越大,多重共线性越严重。一般认为VIF大于10时,存在严重的多重共线性。 -
处理
一旦发现模型中存在多重共线性问题,就应采取某种措施。至于采取什么样的方法来解决,要看多重共线性的严重程度。下面给出多重共线性问题的一些解决办法。- 将一个或多个相关的自变量从模型中剔除,使保留的自变量尽可能不相关。
- 如果要在模型中保留所有的自变量,那就应该:
●避免根据t统计量对单个参数β进行检验。
●对因变量y值的推断(估计或预测)限定在自变量样本值的范围内。
分类自变量
- 定义:含有「分类变量」的自变
- 定义:用虚拟变量/指标变量来模拟:分类自变量的影响的变量
- 使用:分类变量有k个水平,需要定义k-1个虚拟变量,能取值1或者0
- 例如:
1.分类变量:销售区域口,有A,B,C三个水平
2.定义虚拟变量:
x1:I if sales region B 0 otherwise
x2:I if sales region C 0 otherwise
3.建立回归方程
E ( y ) = β 0 + β 1 x 1 + β 2 x 2 E(y)=\beta_0+\beta_1x_1+\beta_2x_2 E(y)=β0+β1x1+β2x2⊙
4.三种变化情况

残差分析
同12-6,简单线性回归的残差分析
Logistic回归
- 略
变量选择与逐步回归
-
意义:如果在建立模型之前能对所收集到的自变量进行一定的筛选,去掉那些不必要的自变量,不仅会使建立模型变得容易,而且使模型更具有可操作性,也更容易解释。
-
原则:
增加/删除变量后对统计量进行显著性检验,最终选择残差图应该撑水平带状 -
检验的根据是:
F检验:将一个或一个以上的自变量引人回归模型中时,是否使残差平方和(SSE)显著减少。
如果增加一个自变量使残差平方和(SSE)显著减少,则说明有必要将这个自变量引入回归模型,否则,就没有必要将这个自变量引入回归模型。确定在模型中引入自变量 x i x_i xi是否使残差平方和(SSE)显著减少的方法,就是使用F统计量的值作为一个标准,以此来确定是在模型中增加一个自变量,还是从模型中剔除一个自变量。

-
向前选择( forward selection)
- 开始模型中没有自变量
- 每次添加变量不允许再从模型中删除!
- 终止条件:模型之外每一个自变量无法加入模型,p值> Alpha-to- Enter
-
向后剔除( backward elimi-nation)
- 开始模型已经包含所有自变
- 每次删除一个自变量不允许再添加回模型!
- 终止条件,模型之内每一个自变量无法被删除,p值<= Alpha-to- Remove
- 注意:前向选择和后向消元③有可能得到③不同的模型
-
逐步回归( stepwise regression)
- 每一步确定
- 已经在模型中的自变量
是否应该被删除,若有p值> Alpha-to- Remove,删除 - if没有自变量能被删除
考虑 - 不在模型中的某个自变量
是否可以被添加,若有p值<= Alpha-to- Enter,添加○具有最小p值的自变量
- 已经在模型中的自变量
- 终止条件
- 没有自变量能 进入模型or被删除
- 特点
某个自变量在某一步可能进入模型,下一步可能被删除,稍后某一步重新进入模型
- 每一步确定
-
最优子集( best subset)
判定系数(R-Sq),越大越好
其他条件都相同使用包含较少自变量的简单模型 -
自相关性&瓦特森检验
略
16时间序列及预测
- 时间序列( times series)
同一现象在不同时间的相继观察值排列而成的序列
分析目:给未来的时间序列提供预测值
时间序列的模式
-
时间序列的成分可以分为四种,即
趋势(T)、季节性或季节变动(S)、周期性或循环波动©、随机性或不规则波动(Ⅰ)。 -
平稳时间序列( stationary series)
定义:这类序列中的各观察值基本上在某个固定的水平上波动,虽然在不同的时间段波动的程度不同,但并不存在某种规律,波动可以看成是随机的,如图

-
非平稳序列( non-stationary series)
包含趋势、季节性或周期性的序列,它可能只含有其中一种成分,也可能含有几种成分。因此,非平稳序列又可以分为有趋势的序列、有趋势和季节性的序列、几种成分混合而成的复合型序列。 -
趋势( trend)
时间序列在长期内呈现出来的某种持续上升或持续下降的变动,也称长期趋势。时间序列中的趋势可以是线性的,也可以是非线性的。

-
季节性( seasonality)也称季节变动( seasonal fluctuation),
它是时间序列在一年内重复岀现的周期性波动。不仅仅是指一年中的四季,其实是指任何一种周期性的变化

-
周期性( cyclicity)
也称循环波动( cyclical fluctuation),是时间序列中呈现出来的围绕长期趋势的一种波浪形或振荡式变动。周期性通常是由商业和经济活动引起的,它不同于趋势变动,不是朝着单一方向的持续运动,而是涨落相间的交替波动;它也不同于季节变动,季节变动有比较固定的规律,且变动周期大多为一年,循环波动则无固定规律,变动周期多在一年以上,且周期长短不一。周期性通常是由经济环境的变化引起的。 -
随机性( randomness),
也称不规则波动( irregular variations)。偶然性因素对时间序列产生影响,致使时间序列呈现出某种随机波动。 -
传统时间序列分析的
把这些成分从时间序列中分离出来,并用一定的数学关系式表示它们之间的关系,而后分别进行分析。按四种成分对时间序列的影响方式不同,时间序列可分解为多种模型,如加法模型( additive model)、乘法模型( multiplicative model)等。其中较常用的是乘法模型,
其形式为: Y t = T t ∗ S t ∗ C t ∗ I t Y_t=T_t*S_t*C_t*I_t Yt=Tt∗St∗Ct∗It
时间序列的描述性分析
- 图形描述
在对时间序列进行分析时,最好是先作一个图,然后通过图形观察数据随时间变化的模式及趋势。
作图是观察时间序列形态的一种有效方法,它对于进一步分析和预测会有很大帮助。 - 增长率分析
增长率是对现象在不同时间里的变化状况所做的描述。由于对比的基期不同,增长率有不同的计算方法。这里主要介绍增长率和平均增长率的计算方法。- 增长率
増长率( growth rate)也称增长速度,它是时间序列中报告期观察值与基期观察值之比减1后的结果,用%表示。由于对比的基期不同,增长率可以分为环比增长率和定基增长率。- 环比增长率
报告期观察值与前一时期观察值之比减1的结果,说明现象逐期增长变化的程度; - 定基增长率
报告期观察值与某一固定时期观察值之比减1的结果,说明现象在整个观察期内总的增长变化程度。
- 环比增长率
- 平均增长率
平均增长率( average rate of increase)也称平均增长速度,它是时间序列中逐期环比值(也称环比发展速度)的几何平均数减1后的结果,
计算公式为:
G ‾ = ( Y 1 Y 0 ) ( Y 2 Y 1 ) ( Y 3 Y 2 ) … ( Y n Y n − 1 ) n − 1 = ( Y n Y 0 ) n − 1 \overline G=\sqrt[n]{(\frac{Y_1}{Y_0})(\frac{Y_2}{Y_1})(\frac{Y_3}{Y_2})…(\frac{Y_n}{Y_{n-1}})}-1=\sqrt[n]{(\frac{Y_n}{Y_{0}})}-1 G=n(Y0Y1)(Y1Y2)(Y2Y3)…(Yn−1Yn)−1=n(Y0Yn)−1
3.増长率分析中应注意的问题
1. 当时间序列中的观察值出现0或负数时,不宜计算增长率。例如,假定某企业连续5年的利润额(单位:万元)分别为5,2,0,一3,2,对这一序列计算增长率,要么不符合数学公理,要么无法解释其实际意义。在这种情况下,适宜直接用绝对数进行分析。
2. 在有些情况下,不能单纯就增长率论增长率,要注意将增长率与绝对值水平结合起来分析。先看一个例子.增长1%的绝对值= 前期水平/100
- 增长率
时间序列预测的程序
-
确定时间序列的类型
- 确定趋势成分是否存在,
- 绘制时间序列的线图入手。观察图13-5,可以看出时间序列中是否存在趋势,以及所存在的趋势是线性的还是非线性的。
- 回归分析拟合一条趋势线,然后对回归系改进行显著性检验。如果回归系数显著,就可以得出线性趋势显著的结论。
- 确定李节成
1. 定义:确定季节成分是否存在
2. 数据:至少需要两年的数据,而且数据需要按季度、月份、周或天等来记录。
3. 方法:绘制时间序列的线图,但需要一种特殊的时间序列图,即年度折叠时间序列图( folded annual time series plot)。
绘制该图时,需要将每年的数据分开画在图上,也就是横轴只有一年的长度,每年的数据分别对应纵轴。
- 确定趋势成分是否存在,
-
找出适合此类时间序列的预测方法。

-
对可能的预测方法进行评估,以确定最佳预测方案。
- 评价的方法:预测误差。预测值与实际值的差距
- 最优的预测方法:也就是预测误差达到最小的方法。选择哪种方法取决于预测者的目标、对方法的熟悉程度等包括:
-
平均误差
设时间序列的第i个观测值为 Y i Y_i Yi,预测值为 F i F_i Fi,所有预测误差 ( Y i − F i ) (Y_i-F_i) (Yi−Fi)的平均数就
是平均误差( mean error),用ME表示,其计算公式为
M E = ∑ i = 0 n ( Y i − F i ) n ME=\frac{\displaystyle\sum_{i=0}^{n}(Y_i-F_i)}{n} ME=ni=0∑n(Yi−Fi)
式中,n为预测值的个数。由于预测误差的数值可能有正有负,求和的结果就会相互抵消,在这种情况下,平均
误差可能会低估误差。 -
平均绝对误差 (mean absolute deviation)
将预测误差取绝对值后计算的平均误差用MAD表示,
平均绝对误差可以避免误差相互抵消的问题,因而可以准确反映实际预测误差的大小,
其计算公式为: M A D = ∑ i = 1 n ∣ Y i − F i ∣ n MAD=\frac{\displaystyle\sum_{i=1}^n{|Y_i-F_i|}}{n} MAD=ni=1∑n∣Yi−Fi∣ -
均方误差( mean square error)
通过平方消去误差的正负号后计算的平均误差,用
MSE表示
其计算公式为
M A D = ∑ i = 1 n ( Y i − F i ) 2 n MAD=\frac{\displaystyle\sum_{i=1}^n{(Y_i-F_i)^2}}{n} MAD=ni=1∑n(Yi−Fi)2 -
平均百分比误差和平均绝对百分比误差等。
ME,MAD和MSE的大小受时间序列数据的水平和计量单位的影响,有时并不能真正反映预测模型的好坏,它们只有在比较不同模型对同一数据的预测时才有意义。
平均百分比误差( mean percentage error)和平均绝对百分比误差( mean absolute percentage
error)则不同,它们消除了时间序列数据的水平和计量单位的影响,是反映误差大小的相对值。
平均绝对误差用MPE表示,其计算公式为:
M P E = ∑ i = 1 n ( Y i − F i ) Y i ∗ 100 % n MPE=\frac{\displaystyle\sum_{i=1}^n{\frac{(Y_i-F_i)}{Y_i}}*100\%}{n} MPE=ni=1∑nYi(Yi−Fi)∗100%
平均绝对百分比误差用MAPE表示,其计算公式为:
M A P E = ∑ i = 1 n ( ∣ Y i − F i ∣ ) Y i ∗ 100 % n MAPE=\frac{\displaystyle\sum_{i=1}^n{\frac{(|Y_i-F_i|)}{Y_i}}*100\%}{n} MAPE=ni=1∑nYi(∣Yi−Fi∣)∗100%
-
-
利用最佳预测方案进行预测。
-
确定趋势成分
平稳序列的预测
平稳时间序列主要是通过对时间序列进行平滑以消除随机波动,因而也称为平滑法。平滑法既可用于对平稳时间序列进行短期预测,也可用于对时间序列进行平滑以描述序列的趋势(包括线性趋势和非线性趋势)。
- 简单平均法
简单平均法是根据已有的t期观察值通过简单平均来预测下一期的数值。设时间序列已有的t期观察值为Y1,Y2,…,Y2,则t+1期的预测值F+1为:
F t + 1 = ∑ i = 1 t ( Y i ) t F_{t+1}=\frac{{\displaystyle\sum_{i=1}^{t}(Y_i)}}{t} Ft+1=ti=1∑t(Yi)
到了t+1期后,有了t+1的实际值,便可计算出t+1期的预测误差e+1:
e t + 1 = Y t + 1 − F t + 1 e_{t+1}=Y_{t+1}-F_{t+1} et+1=Yt+1−Ft+1
于是,t+2期的预测值为:
F t + 1 = ∑ i = 1 t + 1 ( Y i ) t + 1 F_{t+1}=\frac{{\displaystyle\sum_{i=1}^{t+1}(Y_i)}}{t+1} Ft+1=t+1i=1∑t+1(Yi)依此类推。 - 移动平均法
移动平均法( moving average)是通过对时间序列逐期递移求得平均数作为预测值的一种预测方法,其方法有简单移动平均法( simple moving average)和加权移动平均法( weighted moving average)两种。


- 指数平滑法
指数平滑法( exponential smoothing)是通过对过去的观察值加权平均进行预测的种方法,该方法使t+1期的预测值等于t期的实际观察值与t期的预测值的加权平均值。
指数平滑法是加权平均的一种特殊形式,观察值的时间越远,其权数呈现指数下降,因而
称为指数平滑。指数平滑法有一次指数平滑法、二次指数平滑法、三次指数平滑法等


趋势型序列的预测
上面介绍的平滑法只适合平稳时间序列。当序列存在明显的趋势或季节成分时,预测方法可以分为线性趋势和非线性趋势两大类。
如果这种趋势能够延续到未来,就可以利用趋势进行外推预测。有趋势序列的预测方法主要有线性趋势预测、非线性趋势预测和自回归模型预测等。
- 线性趋势预测
线性趋势( linear trend)是指现象随着时间的推移而呈现出稳定增长或下降的线性变化规律。



- 非线性趋势预测
若呈现出某种非线性趋势( non-linear trend),则需要拟合适当的趋势曲线。例如,图13-5(b)和图13-5(c
就有明显的非线性趋势。下面介绍几种常用的趋势曲线。
- 指数曲线
指数曲线( exponential curve)用于描述以几何级数递增或递减的现象,即时间序列的观察值Y按指数规律变化,或者说时间序列的逐期观察值按一定的比率增长或衰减。

- 多阶曲线
有些现象的变化形态比较复杂,它们不是按照某种固定的形态变化,而是有升有降,

13.6复合型序列的分解预测
复合型序列是指含有趋势、季节、周期和随机成分的序列。这类序列的预测方法通常是将时间序列的各个因素依次分解出来,然后进行预测。
由于周期成分的分析需要有多年的数据,实际中很难得到多年的数据,因此采用的分解模为:
Y
=
T
t
×
S
t
×
I
t
Y=T_t×S_t×I_t
Y=Tt×St×It。这一模型表示该时间序列中含有趋势成分、季节成分和
随机成分。这类序列的预测方法主要有季节性多元回归模型、季节自回归模型和时间序列分解法预测等。
季节性多元回归模型已在前面作了介绍,本节主要介绍时间序列分解法预测。分解法预测通常按下面的步骤进行:
第1步:确定并分离季节成分。计算季节指数,以确定时间序列中的季节成分。然后将季节成分从时间序列中分离出去,即用每一个时间序列观察值除以相应的季节指数,以消除季节性。
第2步:建立预测模型并进行预测。对消除了季节成分的时间序列建立适当的预测模型,并根据这一模型进行预测。
第3步:计算最后的预测值。用预测值乘以相应的季节指数,得到最终的预测值。
- 计算季节指数
季节指数( seasonal index)刻画了序列在一个年度内各月或各季度的典型季节特征。在乘法模型中,季节指数是以其平均数等于100%为条件而构成的,它反映了某一月份或季度的数值占全年平均数值的大小。
如果现象的发展没有季节变动,则各期的季节指数应等于100%;如果某一月份或季度有明显的季节变化,则各期的季节指数应大于或小于100%。因此,季节变动的程度是根据各季节指数与其平均数(100%)的偏差程度来测
定的。
- 平均趋势剔除法。该方法的基本步骤是:
-
计算移动平均值
(如果是季度数据,则采用4项移动平均,月份数据则采用12项移动平均),并对其结果进行中心化处理,也就是将移动平均的结果再进行一次二项移动平均,即得出中心化移动平均值(CMA)。 -
计算移动平均的比值
也称为季节比率,即将序列的各观察值除以相应的中
心化移动平均值,然后计算出各比值的季度(或月份)平均值 -
季节指数调整。
由于各季节指数的平均数应等于1或100%,若根据第2步计算的季节比率的平均值不等干1,则需要讲行调整。具体方法是:将第2步计算的每个季节比率的平均值除以他们的总平均值。
- 案例






-
17指数
基本问题
-
介绍
指数,或称统计指数,是分析分析社会经济和预测景气度的重要工具。学习指数,并不在于掌握某种指数的具体计算方法,重要的是体会方法背后蕴藏的统计思想,以便针对具体的硏究对象,依据编制指数的目的,选择或创造最恰当的计算指数。 -
指数概念
指数是测定多项内容数量综合变动的相对数。 -
两个核心要点:
-
实质是测定多项内容:
指数方法论研究如何将多项内容合在一起,从整体上进行反映。单一项目的指数计算简单,不是指数方法论中的核心内容。例如,零售价格指数反映的是零售市场几百万种商品价格变化的整体状况。单一商品价格指数也是有的,例如国家提高烟酒税后,茅台酒价格大幅上升。 -
表现形式为动态相对数:
既然是动态相对数,就涉及指标的基期对比,不同要素基期的选择就成为指数方法需要讨论的问题。
-
-
指数分类
各种分类是从不同的角度对统计指数所做的一般分类,也可以交叉进行复合分类- 按照考察对象的范围和计算方法:个体指数和总指数。
- 个体指数
反映总体中个别现象或个别项目数量变动的相对数,如某种产品的产量指数、某种商品的价格指数等。 - 总指数
综合反映多种项目数量变动的相对数,如多种产品的产量指数、多种商品的价格指数等。由于多种事物的使用价值不同,其数量不具有直接综合的性质,所以总指数的计算不能使用个体指数直接对比的方法,而需要使用专门的方法。
- 个体指数
- 按照所反映指标的性质:数量指标指数和质量指标指数
- 数量指标指数
反映数量指标变动程度的相对数,如商品销售量指数、工业产品产量指数等,数量指标通常采用实物计量单位。 - 质量指标指数
反映品质指标变动程度的相对数,如产品价格指数、产品单位成本指数等,质量指标通常采用货币计量 - 数量指标和质量指标的划分具有相对性。
如单位产品原材料消耗量指标,相对于产品产量指标,它是质量指标;但相对于单位原材料价格指标,它又是数量指标。把指标区分为数量指标和质量指标,更多的是为了讨论问题的方便,而不是真要把指标分成不同类型。
- 数量指标指数
- 按照计算形式不同,可分为简单指数和加权指数
- 简单指数
把计入指数的各个项目的重要性视为相同; - 加权指数
对计入指数的各个项目依据重要程度赋予不同的权数,再进行计算。加权指数可分为两种,即综合形式和平均形式。- 采用综合形式编制的加权指数可称为加权综合指数;
- 采用平均形式编制的加权指数可称为加权平均指数。
- 实际应用
有时由于缺少必要的权数资料,或者由于指数编制的频率或时效性要求较高,会采用适当的简单指数。
- 简单指数
- 按照考察对象的范围和计算方法:个体指数和总指数。
-
指数编制中的问题
-
选择项目
只选择代表性项目。理论上讲,指数是反映总体数量变动的相对数,但实际中将总体全部项目都计算在内往往不可能,也没必要。
例如,编制消费者价格指数时不可能将消费者所消费的所有商品和服务价格全部纳入价格指数,而需要选择:数量有保证,价格趋势有代表性的代表规格品。 -
确定权数
分配权重。指数是对代表项目进行加权得到的结果,如何确定权数是编制指数时必须解决的问题。确定权数的途径大体有两种:- 一种是利用已有的信息构造权数。指数理论要回答选择什么样的数据做权数,以及用什么时期的数据构造权数;
例如,计算零售价格指数时,每个代表规格品用其代表的商品零售额在全部零售额中的比重做权数。关键:是否具有构造权数的数据,以及这些数据的质量。 - 一种是主观权数,常见于社会现象的指数编制。指数理论要回答实际上是将指数方法拓展到哪些指标,如何形成一系列的综合评价方法
例如编制幸福感指数,是将反映幸福感不同侧面的类指数综合,每个类指数的权重是多少,一般由指数编制人员主观决定最后得到总指数。
- 一种是利用已有的信息构造权数。指数理论要回答选择什么样的数据做权数,以及用什么时期的数据构造权数;
-
指数计算方法
指数测定的研究对象不同,编制指数的数据来源不同,总指数的不同计算方法。计算方式由共识,但不唯一,需要从不同角度、用不同方式对这些指数进行选择、改造和完善。
-
总指数编制方法
-
介绍:
总指数是对个体指数的综合,综合有两个途径:-
简单指数:对个体指数的简单汇总,不考虑权数
-
加权指数:编制总指数时考虑权数的作用,根据计算方式不同,又可以分为加权综合指数和加权平均指数。
-
-
简单指数
简单指数的总缺点:
综合和平均都没有考虑到权数的影响,计算结果难以反映实际情况。另外,将使用价值不同的产品个体指数或价格(指标值)相加,既缺乏实际意义,又缺少理论依据。- 简单综合指数
这是将报告期的指标总和与基期的指标总和相对比的指数,该方法的特点是先综合后对比,计算公式为:
I p = ∑ p 1 ∑ p 0 I_p=\frac{\sum p_1}{\sum p_0} Ip=∑p0∑p1
I q = ∑ q 1 ∑ q 0 I_q=\frac{\sum q_1}{\sum q_0} Iq=∑q0∑q1
(式中,p质量指标;q数量指标; I p I_p Ip质量指标指数; I q I_q Iq数量指标指数;下标1—报告期,下标0基期)
优点:在于操作简单,对数据要求少。
缺点:指标值差距大,且变动幅度差异大时,不能反映真实的变动水平。以价格指数为例,在参与计算的商品价格水平有较大差异时,价格低的商品的价格波动会被价格高的商品掩盖。
适用:指标值差距不大的商品。

- 简单平均指数
将个体指数进行简单平均得到的总指数。该方法的计算过程是先对比,后综合,
计算公式为:
I p = ∑ p 1 ∑ p 0 n I_p=\frac{\frac{\sum p_1}{\sum p_0}}{n} Ip=n∑p0∑p1
I q = ∑ q 1 ∑ q 0 n I_q=\frac{\frac{\sum q_1}{\sum q_0}}{n} Iq=n∑q0∑q1

- 简单综合指数
-
加权指数
编制加权指数首先要确定合理的权数,然后根据实际需要确定适当的计算公式。加权指数因所采用的权数不同分为- 加权综合指数,案例:

- 直接汇总没有意义
编制甲、乙、丙三种商品的销售量总指数,需要把各种商品报告期和基期的销售量分别加总,再将两个时期的销售量进行对比。然而,这三种商品的使用价值不同,计量单位也不样,如果销售量直接加总,没有实际意义。同样,若编制这三种商品的价格总指数,把各商品
的价格加总也是没有意义的。 - 引进媒介因素。
在本例中,不同商品的销售量和价格都不能直接加总,因为它们都是不同度量因素。然而每种商品的销售量和价格的乘积即销售额是可以加总的。而且从分析的角度看,销售额的变化恰好反映了销售量增减和价格涨跌两个因素的影响。因此在编制销售量总指数时,可以通过价格这个媒介因素,将销售量转化为可以加总的销售额;而在编制价格总指数时,则可以通过销售量这个媒介因素,将价格转化为可以加总的销售额。 - 将媒介因素固定下来
单纯反映被研究指标的变动情况,按照权数固定时期,分为拉氏指数和帕氏指数。权数时期的选择主要取决于编制指数的目的:- 拉氏指数( Laspeyres index)
将作为权数的同度量因素固定在基期。相应
的计算公式为:
拉氏数量指标指数: I q = ∑ q 1 p 0 ∑ q 0 p 0 I_q=\frac{\sum q_1p_0}{\sum q_0p_0} Iq=∑q0p0∑q1p0
拉氏质量指标指数: I q = ∑ q 0 p 1 ∑ q 0 p 0 I_q=\frac{\sum q_0p_1}{\sum q_0p_0} Iq=∑q0p0∑q0p1
例如:大多数的看法是,计算数量指数(如生产量指数)时,权数(价格)应该定在基期,这样才能剔除价格变动的影响,准确反映生产量的变化,按不变价计算产量指数就是出于这个原因。 - 帕氏指数( Paasche index)
将作为权数的同度量因素固定在报告期
帕氏数量指标指数: I q = ∑ q 1 p 1 ∑ q 0 p 1 I_q=\frac{\sum q_1p_1}{\sum q_0p_1} Iq=∑q0p1∑q1p1
帕氏质量指标指数: I q = ∑ q 1 p 1 ∑ q 1 p 0 I_q=\frac{\sum q_1p_1}{\sum q_1p_0} Iq=∑q1p0∑q1p1
例如:计算质量指数(如价格指数)时,不同时期的权数含义不同:若权数定在基期,反映的是在基期商品(产品)结构下价格的整体变动,更能揭示价格变动的内容;若权数定在报告期,反映的是在现实商品(产品)结构下价格的整体变动,商品(产品)结构变化的影响会融入价格指数,更能揭示价格变动的实际影响。
- 拉氏指数( Laspeyres index)
- 直接汇总没有意义
- 加权平均指数
这是以个体指数为基础,通过对个体指数进行加权平均来编制的指数。
具体步骤为,先计算所研究现象各个项目的个体指数,然后将所给的价值量指标(产值或销售额)作为权数对个体指数进行加权平均。公式简化为:

进一步:
如果权数相对稳定,在计算指数时就不必去搜集 q 0 p 0 ∑ q 0 p 0 \frac{q_0p_0}{\sum q_0p_0} ∑q0p0q0p0, q 1 p 1 ∑ q 1 p 1 \frac{ q_1p_1}{\sum q_1p_1} ∑q1p1q1p1可以采用固定权数的方法,目前,消费价格指数和零售价格指数都是采用这种方法编制的。固定权数多采用比重方法:
I = ∑ i W ∑ W I=\frac{\sum iW}{\sum W} I=∑W∑iW,i为个体指数或类指数;W为权数。
- 区分:????
需要指出,加权综合指数和加权平均指数上述的相同只是形式上的,本质上还是有区别的,主要表现在是全面资料还是样本资料。如果是全面资料,可以采用加权综合指数,计算生产量指数一般属于这种情况,因为生产量指数要包含所有产品的生产情况;而计算价格指数时是无法得到全面资料的,因为市场商品的项目成千上万,全面统计做不到,只能采取选种方法,挑选代表规格品,在这种背景下,若采用加权综合指数,其结果就是仅仅计算了代表规格品的价格变化。价格指数要反映市场所有商品价格的变化,代表规格品是样本,其中的每一项都代表一类商品,每一项代表规格品要有自己的权数。在加权平均指数中,权数的本质是其实就是用代表规格品所代表的那一类商品的销售额在全部销售额中的比重作为权数。在这样的背景下计算指数,只能采取加权平均指数方法。所以,加权平均指数方法主要用于价格指数的计算。这样的背景下计算指数,只能采取加权平均指数方法。所以,加权平均指数方法主要用于价格指数的计算。
- 加权综合指数,案例:
指数体系
-
介绍:一个总量往往可以分解为若干个构成因素,其数量关系可以用指标体系的形式表现出来,可以对现象之间的相互联系作更深入的分析。分析方法的基础是进行因素分解,因素分解的对象可以是总量指数,也可以是平均数指数。
-
指标体系
反映了总量指标与因素指标之间的相互关系,例如:
销售额= 销售量×销售价格
总产值=产量X产品价格
总成本=产量×单位产品成本
销售利润一销售量×销售价格×销售利润率 -
指数体系, 由总量指数及其若干个因素指数构成的数量关系。实质:指标体系转为各指标指数,例如
销售额指数=销售量指数×销售价格指数
总产值指数=产量指数×产品价格指数
总成本指数=产量指数×单位产品成本指数
销售利润指数一销售量指数×销售价格指数×销售利润率指数
- 总量指数体系分析
- 总量指标的两因素分析。
在加权综合指数体系中(加权平均指数相同),为使总量指数等于各因素指数的乘积,
两个因素指数中通常一个为数量指数,另一个为质量指数
各因素指数中权数必须是不同时期的比如数量指数用基期权数加权,质量指数则必须用报告期权数加权,反之亦然。
加权综合指数由于所用权数所属时期不同,可以形成不同的指数体系。但实际分析中比较常用的是基期权数加权的数量指数(拉氏指数)和报告期权数加权的质量指数(帕氏指数)表达式为:
∑ q 1 p 1 ∑ q 0 p 0 = ∑ q 1 p 0 ∑ q 0 p 0 ∗ ∑ q 1 p 1 ∑ q 1 p 0 \frac{\sum q_1p_1}{\sum q_0p_0}=\frac{\sum q_1p_0}{\sum q_0p_0}*\frac{\sum q_1p_1}{\sum q_1p_0} ∑q0p0∑q1p1=∑q0p0∑q1p0∗∑q1p0∑q1p1

- 总量指标的两因素分析。
- 平均数变动因素分解

指数经典案例:
- 总量指数体系分析


- 平均数变动因素分解


几种典型的指数
-
宏观经济指数
- 居民消费价格指数
- 介绍( CPI)
CPI=(一组固定商品按当期价格计算的价值除以一组固定商品按基期价格计算的价值)×100% - 图
- 作用:
- 反映通货膨胀状况。
通 贷 膨 胀 率 = 报 告 期 C P I − 基 期 C P I 基 期 C P × 100 % 通贷膨胀率=\frac{报告期CPI-基期CPI}{基期CP}×100\% 通贷膨胀率=基期CP报告期CPI−基期CPI×100% - 反映居民购买力水平
货 币 购 买 力 指 数 = 1 C P I × 100 % 货币购买力指数=\frac{1}{CPI}×100\% 货币购买力指数=CPI1×100% - 测定职工实际工资水平。
通 实 际 工 资 = 名 义 工 资 C P I × 100 % 通实际工资=\frac{名义工资}{CPI}×100\% 通实际工资=CPI名义工资×100%
- 反映通货膨胀状况。
-
股票价格指数
- 上证指数
- 介绍上证股价指数是由上海证券交易所编制并发布的指数系列,包括上证综合指数、上证180指数、上证50指数、上证380指数等。其中编制最早也最具典型意义的是上证综合指数。
- 上证综合指数
该指数自1991年7月15日起正式发布,以1990年12月19日为基日,基日指数为100点,以现有所有上市股票(包括A股和B股)为样本,以报告期股票发行量为权数进
行编制,计算公式为
今 日 股 价 指 数 = 今 日 市 价 总 值 基 日 市 价 总 值 × 100 今日股价指数=\frac{今日市价总值}{基日市价总值}×100 今日股价指数=基日市价总值今日市价总值×100
市 价 总 值 = 收 盘 价 ∗ 发 行 股 数 市价总值=收盘价*发行股数 市价总值=收盘价∗发行股数,遇发行新股或扩股时,需要进行修正。
- 上证指数
-
消费者满意度指数SCSB
消费者满意度是一个经济心理学的概念,要衡量它就必须建立模型,将消费者满意度与一些相关变量(例如价值、质量、投诉行为、忠诚度等)联系起来。
基本框架模型的前导变量有两个:消费者对产品/服务的价值感知;消费者对产品/服务的期望。满意度的结果变量是消费者投诉和消费者忠诚度忠诚度是模型中最终的因变量,可以作为消费者保留和企业利润的指示器。

可以看出,这是一个结构方程模型,有多个因变量,构成一个原因和结果的关系网,通过模型参数估计,计算各要素的得分,然后计算指数。参数估计可以使用的方法有偏最小二乘方法和结构方程方法,这些是比较专门的统计方法
综合评价指数
- 定义
综合评价指数是将评价结果数量化的一种技术处理,它将多指标进行综合,最后形成概括性的一个指数,通过指数比较达到评价的目的。 - 构成
基础:单项指标,
结合:需要将数据处理技术与指数分析方法结合起来,不同的单项指标通常不能直接进行加减乘除的运算。方法不一定。
原理是:- 建立综合评价指标体系。
所建立的指标体系是否科学与合理,直接关系到评价结果的科学性和准确性。首先应进行必要的定性研究,对所研究的问题进行深入的分析,尽量选择具有一定综合意义的代表性指标。研究结果显示,采用适当的统计方法,如运用多元统计的方法进行指标的筛选,可以提高指标的客观性。 - 评价指标的无量纲化处理。
由于综合评价需要运用由多个指标组成的指数体系,而这些指标的性质不同,计量单位不同,具有不同的量纲,因此需要对各指标的实际数据进行无量纲化处理,使之具有可比性,在此基础上才有可能进行综合。 - 确定各项评价指标的权重。
这是一项重要而又容易引起争议的工作。对于不同的指标,不同的人从不同的角度审视,会有不同的看法和评价,所以在综合评价中如何确定各项指标的权重,一直是学术界讨论的问题。简单地说,确定评价指标的权重有两类方法:- 一类是主观确定权数,可以采用多种方式,但共同特征是由有关专家通过研究讨论决定,特点是可以集中专家集体智慧,工作效率比较高,但很难找到客观的评价标准。
- 另一类是客观确定权数,也有许多不同的实现方法,但共同特征是权数由实际数据确定。例如,经济指标的权数可以是该指标反映的现象的结果(如产值)占总体(总产值)的比重。也有一些研究采用专门的统计方
法,通过模型或其他计算方式产生权数。这类方法的特点是依据数据,客观性更强,但有时难以反映评价的导向性。因为综合评价是有目标性的,提倡什么、强调什么、鼓励什么、突出什么,都可以通过权数反映出来
- 建立综合评价指标体系。
- 计算综合评价指数。
有了各项指标的无量纲化处理结果,有了各项指标的权重,通过适当的方法,就可以得到综合评价指数。通常采用加权平均方法:
I = ∑ i = 1 n z i w i ∑ i = 1 n w i I=\frac{\displaystyle\sum_{i=1}^nz_iw_i}{\displaystyle\sum_{i=1}^nw_i} I=i=1∑nwii=1∑nziwi , 0 ≤ w i ≤ 1 , ∑ w i = 1 0\leq w_i \leq1,\displaystyle\sum {w_i}=1 0≤wi≤1,∑wi=1
当然,综合评价指数的计算并不是最终目的,指数只是一个综合性的描述,重要的是要对这个结果背后的东西进行深入分析,综合评价才有意义,这就是进一步的统计分析问题了。
18非参数方法(略)
背景介绍
符号检验
威尔克克森符号秩检验
曼-惠特尼-威尔克克森检验MWW
克鲁斯卡尔-沃利斯检验
秩相关
18.其他
-
欧氏距离
最常用的距离公式,也叫做欧几里得距离。在二维空间中,两点的欧式距离就是:
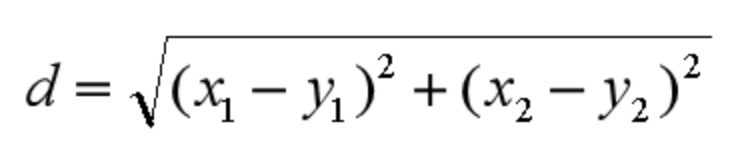
同理,我们也可以求得两点在 n 维空间中的距离:
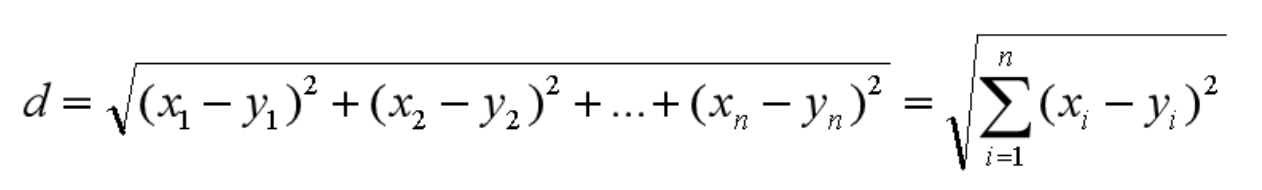
-
曼哈顿距离
在几何空间中用的比较多。以下图为例

绿色的直线代表两点之间的欧式距离,而红色和黄色的线为两点的曼哈顿距离。所以曼哈顿距离等于两个点在坐标系上绝对轴距总和。用公式表示就是:
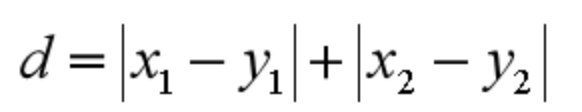
-
闵可夫斯基距离
不是一个距离,而是一组距离的定义。对于 n 维空间中的两个点 x(x1,x2,…,xn) 和 y(y1,y2,…,yn) , x 和 y 两点之间的闵可夫斯基距离为:

其中 p 代表空间的维数,当 p=1 时,就是曼哈顿距离;当 p=2 时,就是欧氏距离;当 p→∞时,就是切比雪夫距离。 -
余弦距离
实际上计算的是两个向量的夹角,是在方向上计算两者之间的差异,对绝对数值不敏感。在兴趣相关性比较上,角度关系比距离的绝对值更重要,因此余弦距离可以用于衡量用户对内容兴趣的区分度。比如我们用搜索引擎搜索某个关键词,它还会给你推荐其他的相关搜索,这些推荐的关键词就是采用余弦距离计算得出的





















 1033
1033











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








