深度学习-线性代数基础

最新推荐文章于 2023-12-16 15:13:02 发布

Mr Gao

最新推荐文章于 2023-12-16 15:13:02 发布

阅读量761

点赞数

分类专栏：数学机器学习

本文链接：https://blog.csdn.net/weixin_43327597/article/details/107199418

版权

机器学习同时被 2 个专栏收录

88 篇文章 11 订阅

订阅专栏

数学

37 篇文章 1 订阅

订阅专栏

深度学习-线性代数

1.1 标量, 向量, 矩阵, 张量

标量 (Scalar): 表⽰⼀个单独的数，通常⽤斜体⼩写字母表⽰，如 s ∈ R, n ∈ N。
向量 (Vector)：表⽰一列数，这些数有序排列的，可以通过下标获取对应值，通常⽤粗体⼩写字母表⽰：x ∈ Rn ，它表⽰元素取实数，且有 n
个元素，第⼀个元素表⽰为：x1。将向量写成列向量的形式：

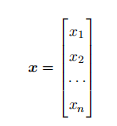
时需要向量的⼦集，例如第 1, 3, 6 个元素，那么我们可以令集合 S = {1, 3, 6} ，然后⽤ xS 来表⽰这个⼦集。另外，我们⽤符号 - 表⽰集合的补
集：xx 1 表⽰除 x1 外 x 中的所有元素，xx S 表⽰除 x1, x3, x6 外 x 中的所有元素。
矩阵 (Matrix): 表⽰⼀个二维数组，每个元素的下标由两个数字确定，通常⽤⼤写粗体字母表⽰：A ∈ Rm×n ，它表⽰元素取实数的 m ⾏ n 列
矩阵，其元素可以表⽰为：A1,1, Am,n。我们⽤ : 表⽰矩阵的⼀⾏或者⼀列：Ai,: 为第 i ⾏，A:,j 为第 j 列。
矩阵可以写成这样的形式：

有时我们需要对矩阵进⾏逐元素操作，如将函数 f 应⽤到 A 的所有元素上，此时我们⽤ $f(A)_{i,j}$ 表⽰。

张量 (Tensor): 超过二维的数组，我们⽤ A 表⽰张量， $A_{i,j,k}$ 表⽰其元素（三维张量情况下）。

import numpy as np
s = 5 # 向量
m = np.array([[1,2], [3,4]])
v = np.array([1,2])
t = np.array([
[[1,2,3],[4,5,6],[7,8,9]],
[[11,12,13],[14,15,16],[17,18,19]],
[[21,22,23],[24,25,26],[27,28,29]],
])
print("标量: " + str(s))
print("向量: " + str(v))
print("矩阵: " + str(m))
print("张量: " + str(t))

标量: 5
向量: [1 2]
矩阵: [[1 2]
[3 4]]
张量: [[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]]

[[11 12 13]
[14 15 16]
[17 18 19]]

[[21 22 23]
[24 25 26]
[27 28 29]]]

1.2 矩阵转置
矩阵转置 (Transpose) 相当于沿着对角线翻转，定义如下：
$A^⊤_{i,j} = A_{i,j}$ (1.3)

矩阵转置的转置等于矩阵本⾝：
$A^⊤)^⊤ = A$ (1.4)

转置将矩阵的形状从 m × n 变成了 n × m 。

向量可以看成是只有一列的矩阵，为了⽅便，我们可以使⽤⾏向量加转置的操作，如： $x = [x1, x2, x3]^⊤$

标量也可以看成是一行一列的矩阵，其转置等于它⾃⾝： $a^⊤ = a$ 。

A = np.array([[1.0,2.0],[1.0,0.0],[2.0,3.0]])
A_t = A.transpose()
print("A:", A)
print("A 的转置:", A_t)

1.3 矩阵加法

加法即对应元素相加，要求两个矩阵的形状⼀样：
$C = A + B, C_{i,j} = A_{i,j} + B_{i,j}$ (1.5)

数乘即一个标量与矩阵每个元素相乘： $D = a · B + c, D_{i,j} = a · B_{i,j} + c$ (1.6)
有时我们允许矩阵和向量相加的，得到⼀个矩阵，把 b 加到了 A 的每⼀⾏上，本质上是构造了⼀个将 b 按⾏复制的⼀个新矩阵，这种机制叫做⼴
播 (Broadcasting)： $C = A + b, C_{i,j} = A_{i,j} + b_{j}$ (1.7)

a = np.array([[1.0,2.0],[3.0,4.0]])
b = np.array([[6.0,7.0],[8.0,9.0]])

print("矩阵相加：", a + b)

矩阵相加：
[[ 7. 9.]
[11. 13.]]

1.4 矩阵乘法

两个矩阵相乘得到第三个矩阵，我们需要 A 的形状为 m × n，B 的形状为 n × p，得到的矩阵为 C 的形状为 m × p： C = AB (1.8)
具体定义为

$C_{i,j} = ∑ A_{i,k}B_{k,j}$ (1.9)

注意矩阵乘法不是元素对应相乘，元素对应相乘又叫 Hadamard 乘积，记作 A ⊙ B。
向量可以看作是列为 1 的矩阵，两个相同维数的向量 x 和 y 的点乘（Dot Product）或者内积，可以表⽰为 $x^⊤y$ 。
我们也可以把矩阵乘法理解为：
$C_{i,j}$ 表⽰ A 的第 i ⾏与 B 的第 j 列的点积。

m1 = np.array([[1.0,3.0],[1.0,0.0]])
m2 = np.array([[1.0,2.0],[5.0,0.0]])
print("按矩阵乘法规则：", np.dot(m1, m2))
print("按逐元素相乘：", np.multiply(m1, m2))
print("按逐元素相乘：", m1*m2)
v1 = np.array([1.0,2.0])

v2 = np.array([4.0,5.0])

print("向量内积：", np.dot(v1, v2))

按矩阵乘法规则： [[16. 2.]
[ 1. 2.]]
按逐元素相乘： [[1. 6.]
[5. 0.]]
按逐元素相乘： [[1. 6.]
[5. 0.]]
向量内积： 14.0

1.5 单位矩阵
为了引⼊矩阵的逆，我们需要先定义单位矩阵 (Identity Matrix)：单位矩阵乘以任意⼀个向量等于这个向量本⾝。记 In 为保持 n 维向量不变的
单位矩阵，即：
In ∈ Rn×n, ∀x ∈ Rn, Inx = x (1.10)
单位矩阵的结构⼗分简单，所有的对⾓元素都为 1 ，其他元素都为 0，如：

I3 = 
1 0 0
0 1 0
0 0 1
np.identity(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])



1.6 矩阵的逆

矩阵 A 的逆 (Inversion) 记作 $A^{-1}$ ，定义为⼀个矩阵使得
$AA^{-1}$ = $I_n$

如果 $A^{-1}$ 存在，那么线性⽅程组 Ax = b 的解为：
$A^{-1}Ax$ = $I_nx$ = x = $A^{-1}b$ (1.13)

A = [[1.0,2.0],[3.0,4.0]]
A_inv = np.linalg.inv(A)
print("A 的逆矩阵", A_inv)
A 的逆矩阵 [[-2. 1. ]
[ 1.5 -0.5]]

1.7 范数
通常我们⽤范数 (norm) 来衡量向量，向量的 Lp 范数定义为：
$x∥p = (∑|x_i|p)^{1/p}$ , p ∈ R, p ≥ 1 (1.14)

L2 范数，也称欧⼏⾥得范数 (Euclidean norm)，是向量 x 到原点的欧几里得距离。有时也⽤ L2 范数的平⽅来衡量向量： $x^⊤x$ 。事实上，平⽅ L2

范数在计算上更为便利，例如它的对 x 梯度的各个分量只依赖于 x 的对应的各个分量，⽽ L2 范数对 x 梯度的各个分量要依赖于整个 x 向量。
L1 范数：L2 范数并不⼀定适⽤于所有的情况，它在原点附近的增长就⼗分缓慢，因此不适⽤于需要区别 0 和⾮常⼩但是⾮ 0 值的情况。L1 范数
就是⼀个⽐较好的选择，它在所有⽅向上的增长速率都是⼀样的，定义为：
$x∥_1 = ∑ |x_i|$ (1.15)
它经常使⽤在需要区分 0 和非 0 元素的情形中。
L0 范数：如果需要衡量向量中⾮ 0 元素的个数，但它并不是一个范数 (不满⾜三⾓不等式和数乘)，此时 L1 范数可以作为它的⼀个替代。
L∞ 范数：它在数学上是向量元素绝对值的最⼤值，因此也被叫做 (Max norm)： $x∥_∞ = max|x_i|$
(1.16)

a = np.array([1.0,3.0])
print("向量 2 范数", np.linalg.norm(a,ord=2))
print("向量 1 范数", np.linalg.norm(a,ord=1))
print("向量无穷范数", np.linalg.norm(a,ord=np.inf))

向量 2 范数 3.1622776601683795
向量 1 范数 4.0
向量无穷范数 3.0

 a = np.array([[1.0,3.0],[2.0,1.0]])
print("矩阵 F 范数", np.linalg.norm(a,ord="fro"))

矩阵 F 范数 3.872983346207417

1.8 特征值分解
如果⼀个 n × n 矩阵 A 有 n 组线性⽆关的单位特征向量 {v(1), . . . , v(n)} ，以及对应的特征值 λ1, . . . , λn。将这些特征向量按列拼接成⼀个矩阵：
V = [v(1), . . . , v(n)]，并将对应的特征值拼接成⼀个向量：λ = [λ1, . . . , λn] 。 A 的特征值分解 (Eigendecomposition) 为：

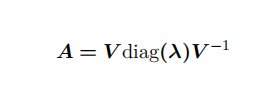
A = V diag(λ)V 졨 1
(1.18)
注意：
• 不是所有的矩阵都有特征值分解
• 在某些情况下，实矩阵的特征值分解可能会得到复矩阵

A = np.array([[1.0,2.0,3.0],
[4.0,5.0,6.0],
[7.0,8.0,9.0]])
# 计算特征值
print("特征值:", np.linalg.eigvals(A))
# 计算特征值和特征向量
eigvals,eigvectors = np.linalg.eig(A)
print("特征值:", eigvals)
print("特征向量:", eigvectors)

特征值: [ 1.61168440e+01 -1.11684397e+00 -3.73313677e-16]
特征值: [ 1.61168440e+01 -1.11684397e+00 -3.73313677e-16]
特征向量: [[-0.23197069 -0.78583024 0.40824829]
[-0.52532209 -0.08675134 -0.81649658]
[-0.8186735 0.61232756 0.40824829]]

1.9 奇异值分解
奇异值分解 (Singular Value Decomposition, SVD) 提供了另⼀种分解矩阵的⽅式，将其分解为奇异向量和奇异值。
与特征值分解相⽐，奇异值分解更加通⽤，所有的实矩阵都可以进⾏奇异值分解，⽽特征值分解只对某些⽅阵可以。
奇异值分解的形式为：

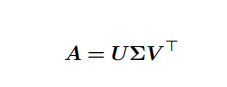
A = UΣV ⊤ (1.19)

若 A 是 m × n 的，那么 U 是 m × m 的，其列向量称为左奇异向量，⽽ V 是 n × n 的，其列向量称为右奇异向量，⽽ Σ 是 m × n 的⼀个对⾓矩
阵，其对⾓元素称为矩阵 A 的奇异值。
事实上，左奇异向量是 $AA^⊤$ 的特征向量，⽽右奇异向量是 $A^⊤A$ 的特征向量，⾮ 0 奇异值的平⽅是 $A^⊤A$ 的⾮ 0 特征值。

A = np.array([[1.0,2.0,3.0],
[4.0,5.0,6.0]])
U,D,V = np.linalg.svd(A)
print("U:", U)
print("D:", D)
print("V:", V)

U: [[-0.3863177 -0.92236578]
[-0.92236578 0.3863177 ]]
D: [9.508032 0.77286964]
V: [[-0.42866713 -0.56630692 -0.7039467 ]
[ 0.80596391 0.11238241 -0.58119908]
[ 0.40824829 -0.81649658 0.40824829]]

1.10 PCA (主成分分析)
假设我们有 m 个数据点 x(1), . . . , x(m) ∈ Rn，对于每个数据点 x(i) ，我们希望找到⼀个对应的点 c(i) ∈ Rl, l < n 去表⽰它 (相当于对它进⾏降维)，并且让损失的信息量尽可能少。

我们可以将这个过程看作是⼀个编码解码的过程，设编码和解码函数分别为 f, g ，则有 f(x) = c, x ≈ g(f(x))。考虑⼀个线性解码函数 g© =
Dc, D ∈ $R_{n×l}$ ，为了计算⽅便，我们将这个矩阵的列向量约束为相互正交的。另⼀⽅⾯，考虑到存在尺度放缩的问题，我们将这个矩阵的列向量约
束为具有单位范数来获得唯⼀解。
对于给定的 x ，我们需要找到信息损失最⼩的 c⋆，即求解：

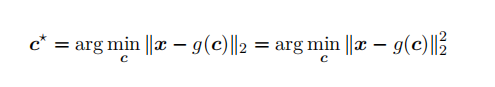c⋆ = arg minc ∥x x g(c)∥2 = arg minc ∥x x g(c)∥22(1 .20)
这⾥我们⽤⼆范数来衡量信息的损失。展开之后我们有：

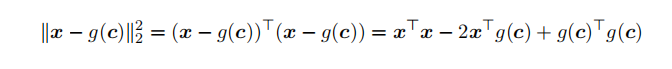
在这里插入图片描述

结合 g© 的表达式，忽略不依赖 c 的 x⊤x 项，我们有：
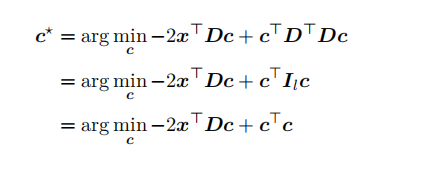c⋆ = arg minc ← 2x⊤Dc + c⊤D⊤Dc= arg minc ← 2x⊤Dc + c⊤Ilc = arg minc ← 2x⊤Dc + c⊤c(1. 22)
这⾥ D 具有单位正交性。

对 c 求梯度，并令其为零，我们有：

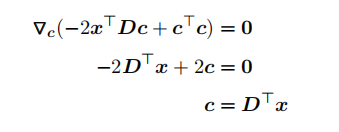
▽c(( 2x⊤Dc + c⊤c) = 0 ← 2D⊤x + 2c = 0 c = D⊤x

(1.23)
因此，我们的编码函数为：

$f(x) = D^⊤x$ (1.24)
此时通过编码解码得到的重构为：

$r(x) = g(f(x)) = DD^⊤x$ (1.25)

接下来求解最优的变换 D 。由于我们需要将 D 应⽤到所有的 $x_i$ 上，所以我们需要最优化：
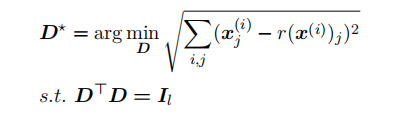D⋆ = arg minD √∑i,j(x(i) j ← r(x(i))j )2s.t. D⊤D = Il(1. 26)
为了⽅便，我们考虑 l = 1 的情况，此时问题简化为：
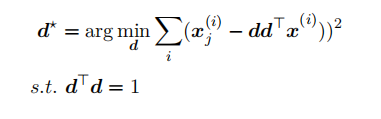d⋆ = arg mind ∑i (x(i) j ← dd⊤x(i)))2s.t. d⊤d = 1(1 .27)
考虑 F 范数，并进⼀步的推导：
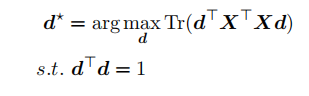d⋆ = arg maxdTr(d⊤X⊤Xd)s.t. d⊤d = 1(1 .28)

优化问题可以⽤特征分解来求解。但实际计算时，我们会采⽤如下⽅式计算：
PCA 将输⼊ x 投影表⽰成 c。c 是⽐原始输⼊维数更低的表⽰，同时使得元素之间线性⽆关。假设有⼀个 m × n 的矩阵 X，数据的均值为零，即
E[x] = 0，X 对应的⽆偏样本协⽅差矩阵： Var[x] = 1 mm 1X⊤X 。
PCA 是通过线性变换找到一个 Var [c] 是对角矩阵的表⽰ c = V ⊤x ，矩阵 X 的主成分可以通过奇异值分解 (SVD) 得到，也就是说主成分是 X
的右奇异向量。假设 V 是 $X = UΣV ^⊤$ 奇异值分解的右奇异向量，我们得到原来的特征向量⽅程：
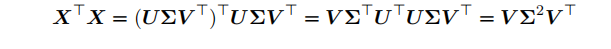
X⊤X = (UΣV ⊤)⊤UΣV ⊤ = V Σ⊤U ⊤UΣV ⊤ = V Σ2V ⊤ (1.29)
因为根据奇异值的定义 $U ^⊤U$ = I 。因此 X 的⽅差可以表⽰为：
Var[x] = 1 mm 1X⊤X = 1 mm 1V Σ2V ⊤。
所以 c 的协⽅差满⾜：
Var[c] = 1 mm 1C⊤C = 1 mm 1V ⊤X⊤XV = 1 mm 1V ⊤V Σ2V ⊤V = 1 mm 1Σ2，
因为根据奇异值定义 $V ^⊤V = I$ 。c 的协⽅差是对
⾓的，c 中的元素是彼此⽆关的。
以 iris 数据为例，展⽰ PCA 的使⽤。

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
%matplotlib inline
[13]: # 载入数据
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df.label.value_counts()


 2 50
1 50
0 50
Name: label, dtype: int64


[14]: # 查看数据



df.tail()


[14]: sepal length sepal width petal length petal width label
145 6.7 3.0 5.2 2.3 2
146 6.3 2.5 5.0 1.9 2
147 6.5 3.0 5.2 2.0 2
148 6.2 3.4 5.4 2.3 2
149 5.9 3.0 5.1 1.8 2
[15]: # 查看数据
X = df.iloc[:, 0:4] y = df.iloc[:, 4] 6深度学习：线性代数 朱明超
print("查看第一个数据： \n", X.iloc[0, 0:4])
print("查看第一个标签: \n", y.iloc[0])

查看第一个数据：
sepal length 5.1
sepal width 3.5
petal length 1.4
petal width 0.2
Name: 0, dtype: float64
查看第一个标签: 0

class PCA():
  def __init__(self):
    pass
  def fit(self, X, n_components):
    n_samples = np.shape(X)[0]
    covariance_matrix = (1 / (n_samples-1)) * (X -         X.mean(axis=0)).T.dot(X - X.mean(axis=0))
# 对协方差矩阵进行特征值分解
    eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)
# 对特征值（特征向量）从大到小排序
    idx = eigenvalues.argsort()[::-1]
    eigenvalues = eigenvalues[idx][:n_components]
    eigenvectors = np.atleast_1d(eigenvectors[:, idx])[:, :n_components]
# 得到低维表示
    X_transformed = X.dot(eigenvectors)
    return X_transformed
[17]: model = PCA()
Y = model.fit(X, 2)
[18]: principalDf = pd.DataFrame(np.array(Y),
columns=['principal component 1', 'principal component 2'])
Df = pd.concat([principalDf, y], axis = 1)
fig = plt.figure(figsize = (5,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_title('2 component PCA', fontsize = 20)
targets = [0, 1, 2]
# ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
colors = ['r', 'g', 'b']
for target, color in zip(targets,colors):
indicesToKeep = Df['label'] == target
ax.scatter(Df.loc[indicesToKeep, 'principal component 1']
, Df.loc[indicesToKeep, 'principal component 2']
, c = color
, s = 50)
ax.legend(targets)
ax.grid()

使⽤ sklearn 包实现 PCA

from sklearn.decomposition import PCA as sklearnPCA
sklearn_pca = sklearnPCA(n_components=2) Y = sklearn_pca.fit_transform(X)
 principalDf = pd.DataFrame(data = np.array(Y), columns = ['principal component 1', 'principal component 2'])
Df = pd.concat([principalDf, y], axis = 1)
fig = plt.figure(figsize = (5,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_title('2 component PCA', fontsize = 20)
targets = [0, 1, 2]
# ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
colors = ['r', 'g', 'b']
for target, color in zip(targets,colors):
      indicesToKeep = Df['label'] == target
      ax.scatter(Df.loc[indicesToKeep, 'principal component 1']
             , Df.loc[indicesToKeep, 'principal component 2']
             , c = color
              , s = 50)
ax.legend(targets)
ax.grid()
[21]: import numpy, pandas, matplotlib, sklearn
print("numpy:", numpy.__version__)
print("pandas:", pandas.__version__)

print("matplotlib:", matplotlib.__version__)
print("sklearn:", sklearn.__version__)

Mr Gao

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
深度学习-线性代数基础

深度学习-线性代数1.1 标量, 向量, 矩阵, 张量标量 (Scalar): 表⽰⼀个单独的数，通常⽤斜体⼩写字母表⽰，如 s ∈ R, n ∈ N。向量 (Vector)：表⽰一列数，这些数有序排列的，可以通过下标获取对应值，通常⽤粗体⼩写字母表⽰：x ∈ Rn ，它表⽰元素取实数，且有 n个元素，第⼀个元素表⽰为：x1。将向量写成列向量的形式：时需要向量的⼦集，例如第 1, 3, 6 个元素，那么我们可以令集合 S = {1, 3, 6} ，然后⽤ xS 来表⽰这个⼦集。另外，我们⽤符号
复制链接

扫一扫