步进电动机及其控制

知识架构框图

一、步进电动机简介

1、步进电机主要功能

1、步进电动机（Stepping Motor，或 Step Motor 、Stepper Motor）是一种可由电脉冲控制运动的特殊电动机，可以通过脉冲信号转换控制的方法将脉冲电信号变换成相应的角位移或线位移。因此步进电动机也被称为脉冲电动机（Pulse Motor）。
2、步进电动机不能直接使用通常的直流或交流电源来驱动，而是需要使用专门的步进电动机驱动器驱动。通过一定的控制方式，可以使步进电动机运动时的角位移或线位移与脉冲数成正比，即其转速或线速度与输入控制脉冲的频率成正比。

2、步进电机控制方向

3、步进电动机可以采用开环控制方式进行控制，使控制系统大为简化。步进电动机可以在较宽的范围内通过改变输入控制脉冲的频率来实现调速，并能够做到快速起动、反转和制动。
4、步进电动机与传统的交直流电动机比较：传统的交直流电动机主要功能是将电能转换成机械能，机电能量转换的效率是衡量它性能优劣的主要指标。对于步进电动机来说，不仅要求电动机完成机电能量转换的功能，还提出了运动控制方面的要求，如实现角速度和角位移的控制，于是工业中常用的高精度角位移控制常用步进电动机进行完成。
5、对于控制应用来说，主要控制指标包括:稳速精度、调速范围、动态响应、跟随精度及定位精度等。在现代高性能运动控制应用中，步进电动机、无刷直流电动机和交流伺服电动机成为主要角色。

3、步进电机电磁原理分析

6、所有电动机运动所需的力都源于电磁力。与交流电动机运动不同的是，步进电动机运动时的所需的电磁力是由定子绕组因通电产生的磁场，对由磁性材料按照一定形状做成的转子磁极的吸引力形成的。
交流电机转动时，定子绕组通电产生旋转磁场，而转子由于形成切割磁力线的等效作用在其内部产生感应电流，与定子绕组产生的旋转磁场相互作用形成运动所需的电磁力，从而产生转子的转动。为了产生运动所需的一定强度的感应电流，交流电动机在原理上就会要求旋转磁场在转速上有一定限制。步进电动机的转动类似于同步电机在同步转动时的状态，即由定子线圈通过电流产生的磁场吸引转子形成转动所需的作用力，磁场的旋转带动转子的运动。在这一过程中并不需要在转子内部产生感应电流及其产生的相应的磁场，可以走一步停一下的即步进的方式运行。
7、步进电动机转动作用力产生形式：
一种是由电磁作用原理产生的

作用力是定/转子两个磁场相互作用的结果，其作用力的来源类似于两个磁铁的同极性相排斥异极性相吸引而产生作用力的现象，目前大部分电机也都是遵循这一原理，例如一般的直流电机和交流电机。

另一种是由磁阻原理产生的

作用力则是由定/转子间气隙磁阻的变化产生的，当定子绕组通电时，产生一个单相磁场作用于转子，由于磁场在转子与定子之间的分布要遵循磁阻最小原则（或磁导最大原则），即磁通总要沿着磁阻最小（磁导最大）的路径闭合，因此，当转子的磁极轴线与定子磁极的轴线不重合时，便会有磁阻力作用在转子上并产生转矩使其趋于磁阻最小的位置，即两轴线重合位置，这类似于磁铁吸引铁质物质的现象。

以上两种产生力矩的方式都被用于步进电动机。
如步进电动机有励磁式、反应式及混合式等 其中励磁式是由电磁作用产生力矩的，而反应式是由磁阻原理产生力矩的。而混合式则同时利用了两种形式的作用。

4、步进电机基本参数

电机固有步距角:	表示控制系统每发一个步进脉冲信号，电动机所转动的角度。
步进电机的相数：指电动机内部的线圈组数，目前常用的有二相、三相、四相、五相步进电动机。
保持转矩：	指步进电动机通电但没有转动时，定子锁住转子的力矩。

二、步进电动机分类

1、 按转矩产生的原理分为

a.反应式步进电动机。
b.励磁式步进电动机。这类步进电动机又分为电磁式与永磁式；
c.混合式步进电动机。同时混合使用前两种方式。

2、按输出转矩的大小分为

a．功率步进电动机(动力式)，转矩一般在1公斤·米以上，可直接用来拖动执行元件；
b．伺服式步进电动机(指示式)，转矩在几百克·厘米以下，多用于控制系统中。

3、 按磁场方向分为

a．横向磁场式步进电动机；
b．纵向磁场式步进电动机。

4、按定转子数目分为

a.单定子式步进电动机；
b.双定子及多定子式步进电动机。

5、按定转子相对位置可分为

a.内定子外转子式步进电动机；
b.外定子内转子式步进电动机；
c.十双定子式(内外定子)步进电动机。

另外也还可按绕组形式(集中、分布)，转向（可逆转、不可逆转)、相数〔单相、两相、三相及多相)等方法分类。

三、步进电动机结构与工作原理

1、步进电动机按产生转距的方式不同可分为反应式、励磁式及混合式三种

（1）、反应式步进电动机的定转子都是凸极结构，是利用磁阻最小原理工作。因为步进电动机凸极转

子的交轴磁阻与直轴磁阻不同，所以引起电枢反应磁场按照磁阻最小原理产生电磁转矩，从而驱动转子

转动。反应式步进电动机转子齿数可以很多，因此步距角可以做得很小，即使没有减速装置，也可以低

速、高精度地实现位置控制。

（2）、励磁式步进电动机的励磁可以是永磁式或电磁励磁式，通常是永磁式励磁。励磁式步进电动机

转子由于具有磁场，驱动转矩较大，但由于制造工艺的缘故，转子磁极数目不能做的太多，因此步距角

比较大。

（3）、混合式步进电动机兼有反应式步进电动机和永磁式步进电动机的优点，可以做到步距角小而驱

动转矩又大。

2、单定子三相反应式步进电动机

结构

工作原理

1、磁阻式转矩产生的原理：在定子绕组由于通电产生的相应的电磁场的作用下，在定子小齿与转子小

齿之间存在磁场，转子小齿将被强行推动到最大磁导率（或者最小磁阻）的位置（如图6.2a所示，即定

子小齿与转子小齿对齐的位置），这一过程称为对齿，并处于平衡状态。同时在这一过程中形成转子的

转动。

2、电流换相：当定子小齿与转子小齿对齐后，将不再产生使转子转动的磁力，为了持续形成转动，必

须使其它没有对齐的即错齿（如图6.2b所示）的定子小齿与转子小齿产生磁力，并由磁阻作用形成转

矩。这一过程中即是步进电动机的电流换相。

错齿的存在是步进电动机能够旋转的前提条件。所以，在步进电动机的结构中必须保证有错齿的存在，

也就是说，当某一相处于对齿状态时，其他相必须处于错齿状态。

3、三相步进电机

结构及等效电路图

反应式步进电机

当定子绕组通电及换相时，将会产生使转子转动的力矩并使转子转动。根据通电及换相的方法的不同，可以有以下几种转动方式：

1）通电方式为U—V—W—U…的顺序轮流供电且一相通电、两相断电的方式。此时步进电动机每换一次通电方式，转子按顺时针方向转过60°。如果按U—W—V—U…顺序轮流供电，则步进电动机逆时针转动。称这种方式为“三相三位”或“单三拍”分配方式。

2）通电方式为U—UV—V—VW—W—WU—U…(或反顺序)，则称为“三相六位”或“三相六拍”。此时，步进电动机每步为30°，步距角减小一半。

3）如果通电方式为UV—VW—WU—UV…，则称为‘双三拍”，步距角仍为60°。

反应式步进电动机，除上面介绍的单段式以外，还可以把定子分成三段，称为三段式步进电动机。此

外，还可以把相数做成四相、五相、六相等．对于反应式步进电动机，绕组电流只要求向一个方向流

动，故驱动电路采用单极性驱动。

励磁式步进电机

永磁式与磁阻式的主要区别是转子用永久磁钢做成。转子极数2pr可以为一对极、二对极或多对极，呈星状。定子相数m有二相或多相，做成凸极无小齿。定子极数2pt，为转子极数的相数m倍，即 2mpr＝2pt 。

混合式步进电动机

可分为永磁混合式步进电动机和电磁混合式步进电动机两种。

永磁混合式步进电动机的典型结构，定子结构与单段磁阻式步进电动机相同，定子铁芯的凸极式磁极弧

面有与转子齿形相同的小齿。每个极上安装有控制绕组，绕组的连接方式同永磁式步进电动机一样接

A、B两相，每相绕组按正、反交替串联，转子由环形永久磁铁和两个有小齿的铁芯组成。永磁环为轴

向极性，永磁环两端上各套一转子铁芯，两端铁芯彼此错开1／2齿距．一端铁芯上各齿的极性均相同。

四、步进电动机的矩角特性

步进电动机不改变通电方式的状态称为静态运行状态。步进电动机的静态运行特性，主要是转矩T与偏离角θ的关系，T＝f (θ)，称为矩角特性。

当磁阻式步进电动机通电时，定子齿对转子齿将有吸引磁力，如图6.11所示，当转子齿与定子齿对齐时，两齿的轴线重合θ＝0，转子受到的磁力只有径向力而没有切向力，所以没有电磁转矩，T ＝ 0，此称为初始稳定平衡点，也称为协调点；当两齿错开θ角时，电磁转距应为
                              T= Tmsinθ                
式中θ为转子齿与定子齿的轴线错开的电角度。以一个转子齿距角规定为360o电角度。θ角为转子离开协调位置的角度，所以称为失调角。

从上图可知，步进电动机的转矩随转角位置的不同而不同，是脉动的。我们平时所说的转矩是整步转矩的平均值。一般把步进电动机的输出转矩与脉冲频率的关系称作矩频特性，即步进电动机的机械特性。

步进电动机的失步：
步进电动机脉冲频率不能过高，当脉冲频率过高时，由于转动力矩大小有一定范围，其起动加速度也会

在一定范围内，过高的脉冲频率会使转子的转动速度跟不上输入脉冲控制要求的转动速度，从而导致转

子转动落后于定子磁场的转速，这种情况称为步进电动机的失步。

五、步进电动机的传递函数

步进电动机本身有很多非线性因素(如涡流的影响、矩角特性的非线性等)，因此分析其动特性只能采取近似的方法。
上图示出步进电动机定、转子的三种位置。
a为稳定的平衡位置，b为不平衡位置，c为不稳定平衡位置。

步进电机的传递函数为：

动态结构图为：

六、步进电动机的运动控制

1、步进电动机驱动方法

单极性驱动电路

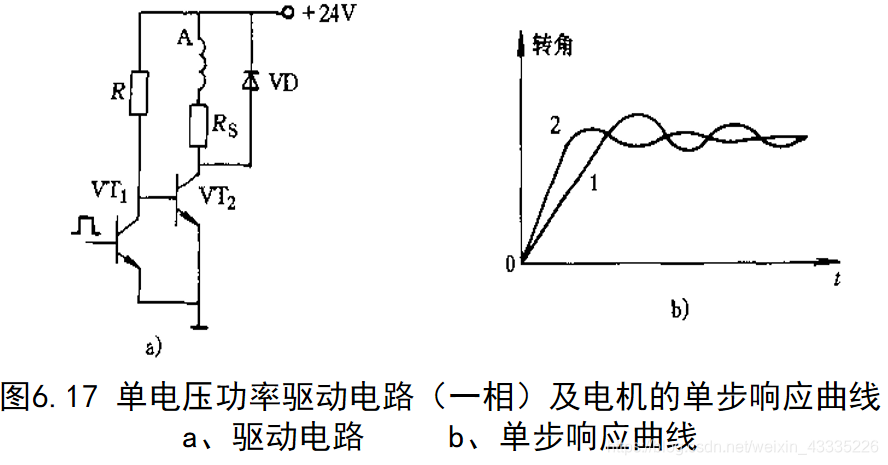
单电压功率驱动电路

高低压驱动电路
斩波恒流驱动电路