图神经网络（三）GCN的变体与框架（3）R-GCN

3.3 R-GCN

 在之前介绍的所有GNN的变体模型中，都没有显式地考虑节点之间关系的不同，相较于同构图，现实生活中的图数据往往是异构的，即图里面存在不止一种类型的关系。本节要介绍的R-GCN就是将图卷积神经网络拓展到这种场景的图数据中去 [0] 。

3.3.1 知识图谱

 一种最典型的包含多种关系的图数据就是知识图谱（Knowledge Graph）。知识图谱是一种规模非常庞大的语义网络，其主要作用是描述通用或专用场景下实体间的关联关系，主要应用场景为搜索引擎、语音助手、智能问答等。

 举一个简单的例子，当我们在Google上搜索“欧拉”时，结果返回页的右边栏会出现一个卡片。如图3-6所示，里面除了有对数学家欧拉的成就介绍外，还分门别类地列出来一些基本情况：生卒年、家庭、教育等信息。搜索引擎能够以这么简单明了的形式列出任务的相关知识，背后离不开知识图谱技术的支持。图3-6的右图将卡片中的一些信息以知识图谱的形式展现了出来。

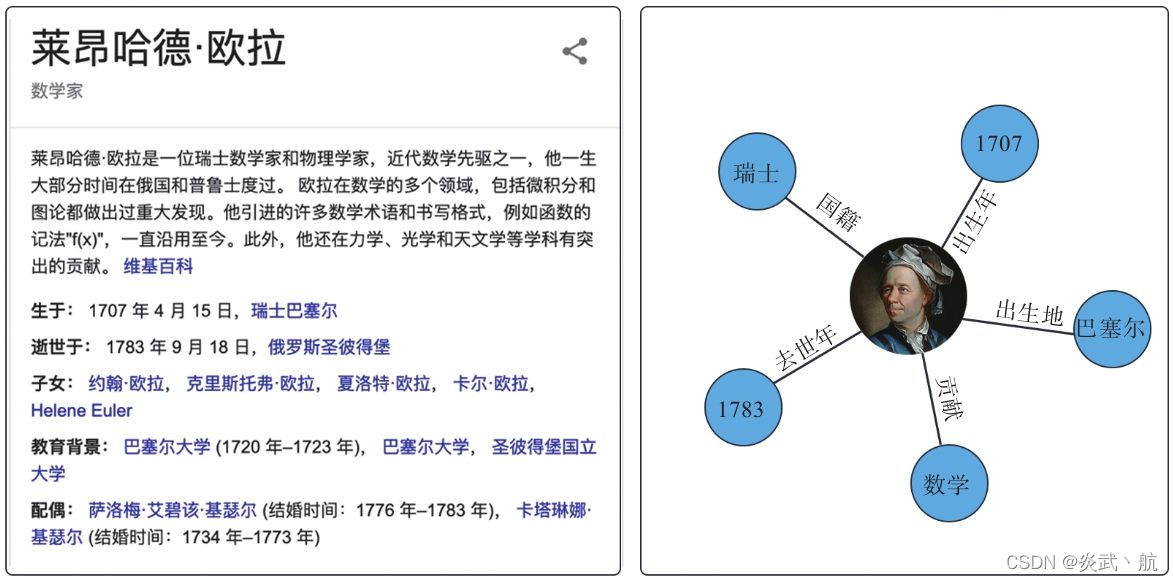
图3-6 Google搜索“欧拉”返回的结果 [1]

 知识图谱的构建所依赖的核心技术是信息抽取与知识构建，该项技术只在从大规模非结构化的自然语言文本中抽取出结构化信息，该技术决定了知识图谱可持续扩增的能力。而对于一个已有的知识图谱，有的时候还需要基于现存的实体间的关系，通过推理学习得到实体间新的关系并将其补充进知识图谱里面去。作为图数据的一种通用学习手段，将GNN应用到该任务上的最大的问题在于如何考量实体间的各种不同关系，而且往往这些关系会有上千种之多，发生过拟合的风险非常高。

[1] 图片来源：https://zh.wikipedia.org/wiki/莱昂哈德·欧拉。

3.3.2 R-GCN

 R-GCN [7] 基于GCN的聚合邻居的操作，又增加了一个聚合关系的维度，，使得节点的聚合操作变成一个双重聚合的过程，其核心公式如下：
$${\mathbf{h}}_i^{(l+1)}=\sigma (\sum _{r\in R}\sum _{v_j\in N_{v_i}^{(r)}}\frac{1}{c_{i,r}}{W}_r^{(l)}{\mathbf{h}}_j^{(l)}+W_o^{(l)}{\mathbf{h}}_i^{(l)})$$
 $R$ 表示图例所有的关系集合，$N_{v_i}^{(r)}$ 表示与节点 $v_i$ 具有 $r$ 关系的邻居集合。$c_{i,r}$ 用来做归一化，比如取 $c_{i,r}=|N_{v_i}^{(r)}|$ 。$W_r$ 是具有 $r$ 关系的邻居对应的权重参数，$W_o$ 是节点自身对应的权重参数。

 由于GCN考虑的是同构图建模，节点之间只存在一种关系，因此GCN只需要一组权重参数来对节点的特征进行变换。R-GCN考虑的是异构图建模，在处理邻居的时候，考量关系的因素对邻居进行分类操作：对于每一种关系的邻居引入不同的权重参数，分别对属于同一关系类型的邻居聚合之后，在进行一次总的聚合，如图3-7所示。

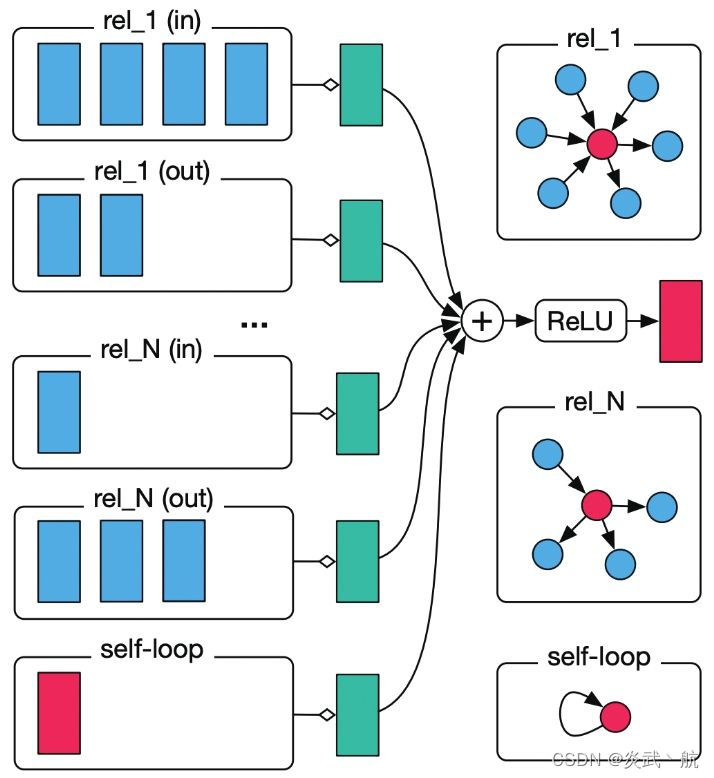
图3-7 R-GCN聚合邻居操作 [1]

 图3-7所示为R-GCN聚合邻居操作的示意图，我们可以清晰地看到这是一个两层的聚合操作：先对同种关系的邻居进行单独聚合，这里对于每一种关系，也同时考虑了关系的正反方向，同时对于自身加入了自连接的关系，在将上述所有不同关系的邻居进行聚合之后，在进行一次总的聚合。

 之前我们提到，一个典型的多关系图数据——知识图谱往往包含着大量的关系。如果我们为每一种关系都设计一组权重，那么单层R-GCN需要学习的参数量僵尸粉庞大，同时，由于不同关系的节点数量是不一样的，对于一些不常见的关系而言，其权重参数对应的学习数据非常少，这大大增加了过拟合的风险。为了避免上述情况发生，R-GCN提出了对 $W_r$ 进行基分解（basic decomposition）的方案，即：
$$W_r=\sum _{b=1}^B{a}_{rb}{V}_b$$
 我们称 $V_b\in R^{d^{(l+1)}\times d^{(l)}}$ 为基，$a_{rb}$ 是 $W_r$ 在 $V_b$ 上的分解系数，$B$ 是超参数，控制着 $V_b$ 的个数，$V_b$ 、$a_{rb}$ 是取代 $W_r$ 需要学习的参数。通过上式的基分解，我们将 $W_r$ 变成了一组基的线性加和，且对于 $|R|$ 组 $W_r$ ，可以反复利用 $|B|$ 组基进行线性加和表示。这样做的好处在于，首先，将需要学习的参数减至原来的$$\frac{B\times d^{(l+1)}\times d^{(l)}+|R|\times B}{|R|\times d^{(l+1)}\times d^{(l)}}$$，在实际训练的时候，我们可以设置一个较小的 $B$ 值，使得$$B\ll \text{min}(|R|\times d^{(l+1)}\times d^{(l)})$$；其次，基 $V_b$ 的优化是所有的常见或者不常见关系所共享的，这种共享的优化参数可以有效防止非常见关系上过拟合现象的出现。基分解是一种非常长喊的数据变换的表示方式（图信号的傅里叶变换中也体现了这种思想），在机器学习中，其作为一种重要的数据处理技巧得到了广泛的应用。

参考文献

[0] 刘忠雨, 李彦霖, 周洋.《深入浅出图神经网络: GNN原理解析》.机械工业出版社.

[1] Schlichtkrull M ， Kipf T N ， Bloem P ， et al.Modeling relational data with graph convolutional networks[C]//European Semantic Web Conference.Springer ， Cham，2018：593-607.

[7] Schlichtkrull M，Kipf T N，Bloem P，et al.Modeling relational data with graph convolutional networks[C]//European Semantic Web Conference.Springer，Cham，2018：593-607.