VAMP由浅入深（Part-1：由消息传递直接推导）

Vector Approximate Message Passing, VAMP

前言

事实上，到今天为止，我才知道AMP/VAMP的推导方式并不局限，而且多种多样。此篇博客所介绍的VAMP推导方法基于期望传播算法（Expecation Propagation, EP），相对来说较为简单，也便于理解。

问题模型

考虑要从观测信号
$$\mathbf{y}={\mathbf{A}\mathbf{x}}^0+\mathbf{w}\in {\mathbb{R}}^M\text{\hspace{1em}(1)}$$
中恢复向量${\mathbf{x}}^0\in {\mathbb{R}}^N$，其中，$\mathbf{A}\in {\mathbb{R}}^{M\times N}$已知。对于该问题，主要有以下两种解决思路：
思路1（优化方向）：
$$\widehat{x\text{x}x}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathbf{x}\in {\mathbb{R}}^{\mathrm{N}}}{\min }\frac{1}{2}{\Vert \mathbf{y}-\mathbf{A}\mathbf{x}\Vert }_2^2+f\left(\mathbf{x}\right)\text{\hspace{1em}(2)}$$
式(2)中的$f(x\text{x}x)$的选取是为了提升估计$\widehat{x\text{x}x}$的结构性，比如选取$f(x\text{x}x)=\lambda {\Vert x\text{x}x\Vert }_1$是考虑到${\mathbf{x}}^0$的稀疏性。
思路2（贝叶斯方向）：
MAP估计
$$\text{MAP: }{\widehat{x\text{x}x}}_{\text{MAP}}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathbf{x}}{\max }p(x\text{x}x|y\text{y}y)=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathbf{x}}{\max }p(y\text{y}y|x\text{x}x)p(x\text{x}x)\text{\hspace{1em}(3)}$$

MMSE估计
$$\text{MMSE: }{\widehat{x\text{x}x}}_{\text{MMSE}}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\tilde{\mathbf{x}}}{\min }\int {\Vert \mathbf{x}-\tilde{\mathbf{x}}\Vert }^{2}p(x\text{x}x|y\text{y}y)\text{d}x\text{x}x=\mathbb{E}[x\text{x}x|y\text{y}y]\text{\hspace{1em}(4)}$$

后验概率密度函数
{ p ( x n ∣ y ) } n = 1 N (5) {\{p(x_n|\pmb y)\}}^N_{n=1} \tag{5} {p(xn​∣y​y​​y)}n=1N​(5)

优化和贝叶斯的共通性：若式（1）中观测信号被高斯噪声破坏，即$w\text{w}w\sim \mathcal{N}(0\text{0}0,{{\gamma }_{\omega }}^{-1}I\text{I}I)$，那么当MAP准则中的先验概率$p(x\text{x}x)$与优化中的正则项$f(x\text{x}x)$满足
$$p(x\text{x}x)\propto \exp [-{\gamma }_{\omega }f(x\text{x}x)]\text{\hspace{1em}(6)}$$
时，认为式（2），即该优化方法与MAP等效。

AMP与贝叶斯推理的简要介绍

若$x\text{x}x$的先验分布满足元素之间独立同分布（i.i.d.），那么
$$p(x\text{x}x)=\prod _{n=1}^{N}p(x_n)\text{\hspace{1em}(7)}$$
对于AMP算法所使用的滤波函数，这里考虑依据以下两个准则分别建立：
准则1（MAP）：滤波函数为（$k$表示迭代次数，${\gamma }_k$表示AMP状态演化时的噪声精度）
$${\mathrm{g}}_1\left(r_{kn},{\gamma }_k\right)=\mathrm{a}\mathrm{r}\mathrm{g}\underset{x_n\in \mathbb{R}}{\min }\left[\frac{{\gamma }_k}{2}{\left|x_n-r_{kn}\right|}^2-\ln p\left(x_n\right)\right]\text{\hspace{1em}(8)}$$
准则2（MMSE）：滤波函数为
$${\mathrm{g}}_1\left(r_{kn},{\gamma }_k\right)={\mathbb{E}}_{p(x_n|r_{kn},{\gamma }_k)}\left[x_n|r_{kn},{\gamma }_k\right]\text{\hspace{1em}(9)}$$
其中，
$$p(x_n|r_{kn},{\gamma }_k)\propto \exp \left[-\frac{{\gamma }_k}{2}{\left|x_n-r_{kn}\right|}^2+\ln p\left(x_n\right)\right]\text{\hspace{1em}(10)}$$
事实上，式（10）中的$p(x_n|r_{kn},{\gamma }_k)$可以被看作是AMP在第$k$次迭代下的后验概率$p(x_n|y\text{y}y)$。另外，对于式（9）所描述的MMSE滤波函数${\mathrm{g}}_1\left(r_{kn},{\gamma }_k\right)$关于$r_{kn}$的一阶导为：
$${\mathrm{g}}_1^{\prime }\left(r_{kn},{\gamma }_k\right)={\gamma }_k\text{var}[x_n|r_{kn},{\gamma }_k]\text{\hspace{1em}(11)}$$
AMP的算法描述

AMP算法中的第7行，“Select ${\gamma }_{k+1}$”建议使用
$${\gamma }_{k+1}=\frac{M}{{\Vert {v\text{v}v}_k\Vert }^2}\text{\hspace{1em}(12)}$$
其中${v\text{v}v}_k$是第$k$次迭代线性估计（第5行）的残差。

基于期望传播的VAMP推导

我们将联合概率密度函数做分解：
$$p(y\text{y}y,x\text{x}x)=p(x\text{x}x)\mathcal{N}(y\text{y}y;Ax\text{Ax}Ax,{{\gamma }_{\omega }}^{-1}I\text{I}I)\text{\hspace{1em}(13)}$$
进一步引入Dirac符号，把$x\text{x}x$拆分为两个等价的向量${x\text{x}x}_1$和${x\text{x}x}_2$，则式（13）可分解为
$$p(y\text{y}y,{x\text{x}x}_1,{x\text{x}x}_2)=p({x\text{x}x}_1)\delta ({x\text{x}x}_1-{x\text{x}x}_2)\mathcal{N}(y\text{y}y;A\text{A}A{x\text{x}x}_2,{{\gamma }_{\omega }}^{-1}I\text{I}I)\text{\hspace{1em}(13)}$$
式（13）分解结果所对应的因子图为

图1：VAMP推导所使用的因子图

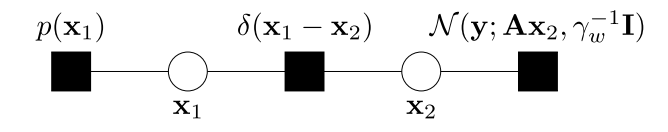
可以看出，该因子图的变量节点为向量形式而非标量。这里首先定义一下三个消息传递规则：

1. 规则1（估计信念）：在变量节点$x\text{x}x$上的估计信念（Approximate Beliefs）$b_{app}(x\text{x}x)=\mathcal{N}(x\text{x}x;\widehat{x\text{x}x},{\eta }^{-1}I\text{I}I)$，其中
   $$\{\begin{array}{l}\widehat{x\text{x}x}={\mathbb{E}}_{b_{sp}}[x\text{x}x]\\ {\eta }^{-1}=<\text{diag}({\text{Cov}}_{b_{sp}}[x\text{x}x])>\end{array}\text{\hspace{1em}(14)}$$
   其中，$b_{sp}(x\text{x}x)$表示所有到变量节点$x\text{x}x$的信念之积，即$b_{sp}(x\text{x}x)\propto {\prod }_i{\mu }_{f_i\to \mathbf{x}}(x\text{x}x)$。
2. 规则2（变量节点到因子节点的消息）：本质上与经典的和积算法一致，假设消息从变量节点$\mathbf{x}$传递到相邻的一个因子节点$f_i$，那么
   $${\mu }_{\mathbf{x}\to f_i}(\mathbf{x})\propto \frac{b_{app}(x\text{x}x)}{{\mu }_{f_i\to \mathbf{x}}(x\text{x}x)}\text{\hspace{1em}(15)}$$
3. 规则3（因子节点到变量节点的消息）：本质上与经典的和积算法一致，假设消息从因子节点$f$传递到相邻的一个变量节点${\mathbf{x}}_i$，那么
   μ f → x i ( x i ) ∝ ∫ f ( x i , { x j } j ≠ i ) ∏ j ≠ i μ x j → f d x j (16) \mu_{f \rightarrow \boldsymbol x_i} (\boldsymbol x_i) \propto \int f(\boldsymbol x_i,{\{ \boldsymbol x_j \}}_{j \neq i}) \prod_{j \neq i} \mu_{\boldsymbol x_j \rightarrow f} \text{d} \boldsymbol x_j \tag{16} μf→xi​​(xi​)∝∫f(xi​,{xj​}j​=i​)j​=i∏​μxj​→f​dxj​(16)

在下面的推导中，我们使用索引$k$表示第$k$次迭代，用$n$表示向量的第$n$个元素。

第一步（初始化）：$k=0$时，初始化消息${\mu }_{\delta \to {\mathbf{x}}_1}({\mathbf{x}}_1)=\mathcal{N}({\mathbf{x}}_1;{\mathbf{r}}_{10},{{\gamma }_{10}}^{-1}\mathbf{I})$，以下几个步骤交替迭代（for $k=0,1,\dots$）

第二步（${\mathbf{x}}_1$处的信念估计）：变量节点${\mathbf{x}}_1$在和积算法操作下的真实信念为$b_{sp}({\mathbf{x}}_1)\propto p({\mathbf{x}}_1)\mathcal{N}({\mathbf{x}}_1;{\mathbf{r}}_{1k},{{\gamma }_{1k}}^{-1}\mathbf{I})$，其均值为${\hat{\mathbf{x}}}_{1k}=\mathbb{E}[{\mathbf{x}}_1|b_{sp}({\mathbf{x}}_1)]$，”平均方差“为${\eta }_{1k}^{-1}=<\text{diag}(\text{Cov}[{\mathbf{x}}_1|b_{sp}({\mathbf{x}}_1)])>$（”平均方差“这个概念只是为了好叙述，实质上表示的是该分布协方差矩阵对角元素的均值）。进一步使用估计信念$b_{app}({\mathbf{x}}_1)=\mathcal{N}({\mathbf{x}}_1;{\hat{\mathbf{x}}}_{1k},{\eta }_{1k}^{-1}I\text{I}I)$来近似，联合式（9）(滤波函数使用MMSE准则)，可以写出
$$\{\begin{array}{l}[{\hat{\mathbf{x}}}_{1k}{]}_n={\mathrm{g}}_1\left(r_{kn},{\gamma }_k\right)\\ {\eta }_{1k}^{-1}={{\gamma }_{1k}}^{-1}{{\mathrm{g}}_1}^{\prime }\left(r_{kn},{\gamma }_k\right)\end{array}\text{\hspace{1em}(17)}$$
第三步（消息传递）：从变量节点${\mathbf{x}}_1$到因子节点$\delta$的消息为
$${\mu }_{{\mathbf{x}}_1\to \delta }({\mathbf{x}}_1)\propto \frac{\mathcal{N}({\mathbf{x}}_1;{\hat{\mathbf{x}}}_{1k},{\eta }_{1k}^{-1}I\text{I}I)}{\mathcal{N}({\mathbf{x}}_1;{\mathbf{r}}_{1k},{{\gamma }_{1k}}^{-1}\mathbf{I})}\text{\hspace{1em}(18)}$$
又因为
$$\frac{\mathcal{N}(\mathbf{x};\hat{\mathbf{x}},{\eta }^{-1}I\text{I}I)}{\mathcal{N}(\mathbf{x};\mathbf{r},{\gamma }^{-1}I\text{I}I)}\propto \mathcal{N}(\mathbf{x};(\hat{\mathbf{x}}\eta -\mathbf{r}\gamma )/(\eta -\gamma ),({\eta -\gamma )}^{-1}I\text{I}I)\text{\hspace{1em}(19)}$$
将式(18)带入到式(19)中，得到${\mu }_{{\mathbf{x}}_1\to \delta }({\mathbf{x}}_1)=\mathcal{N}({\mathbf{x}}_1;{\mathbf{r}}_{2k},{{\gamma }_{2k}}^{-1}I\text{I}I)$，其中
$$\{\begin{array}{l}{\mathbf{r}}_{2k}=({\hat{\mathbf{x}}}_{1k}{\eta }_{1k}-{\mathbf{r}}_{1k}{\gamma }_{1k})/({\eta }_{1k}-{\gamma }_{1k})\\ {\gamma }_{2k}^{}={\eta }_{1k}-{\gamma }_{1k}\end{array}\text{\hspace{1em}(20)}$$
进一步，从因子节点$\delta$到变量节点${\mathbf{x}}_2$的消息为
$${\mu }_{\delta \to {\mathbf{x}}_2}({\mathbf{x}}_2)=\int \delta ({\mathbf{x}}_1-{\mathbf{x}}_2){\mu }_{{\mathbf{x}}_1\to \delta }({\mathbf{x}}_1)\text{d}{\mathbf{x}}_1={\mu }_{{\mathbf{x}}_1\to \delta }({\mathbf{x}}_2)\text{\hspace{1em}(21)}$$
因此，${\mu }_{\delta \to {\mathbf{x}}_2}({\mathbf{x}}_2)=\mathcal{N}({\mathbf{x}}_2;{\mathbf{r}}_{2k},{{\gamma }_{2k}}^{-1}I\text{I}I)$
第四步（${\mathbf{x}}_2$处的信念估计）：类似第二步，在变量节点${\mathbf{x}}_2$处的真实信念为$b_{sp}({\mathbf{x}}_2)\propto \mathcal{N}({\mathbf{x}}_2;{\mathbf{r}}_{2k},{{\gamma }_{2k}}^{-1}I\text{I}I)\mathcal{N}(\mathbf{y};{\mathbf{A}\mathbf{x}}_2,{{\gamma }_{\omega }}^{-1}I\text{I}I)$，其均值和方差分别为
$$\{\begin{array}{l}{\hat{\mathbf{x}}}_{2k}={\left({\gamma }_{\omega }{\mathbf{A}}^T\mathbf{A}+{\gamma }_{2k}I\text{I}I\right)}^{-1}\left({\gamma }_{\omega }{\mathbf{A}}^T\mathbf{y}+{\gamma }_{2k}+{\mathbf{r}}_{2k}\right)\\ \text{Cov}[{\mathbf{x}}_2|b_{sp}({\mathbf{x}}_2)]={\left({\gamma }_{\omega }{\mathbf{A}}^T\mathbf{A}+{\gamma }_{2k}I\text{I}I\right)}^{-1}\end{array}\text{\hspace{1em}(22)}$$
依据规则一，令${\mathbf{x}}_2$处的估计信念为$\mathcal{N}({\mathbf{x}}_2;{\hat{\mathbf{x}}}_{2k},{\eta }_{2k}^{-1}I\text{I}I)$，则${\hat{\mathbf{x}}}_{2k}$直接可得，${\eta }_{2k}^{-1}=<\text{diag}(\text{Cov}[{\mathbf{x}}_2|b_{sp}({\mathbf{x}}_2)])>$。
令
$${\mathrm{g}\text{g}\mathrm{g}}_2({\mathbf{r}}_{2k},{\gamma }_{2k}):={\left({\gamma }_{\omega }{\mathbf{A}}^T\mathbf{A}+{\gamma }_{2k}I\text{I}I\right)}^{-1}\left({\gamma }_{\omega }{\mathbf{A}}^T\mathbf{y}+{\gamma }_{2k}+{\mathbf{r}}_{2k}\right)\text{\hspace{1em}(23)}$$
并且有
$$<{\mathrm{g}\text{g}\mathrm{g}}_2^{\prime }({\mathbf{r}}_{2k},{\gamma }_{2k})>=\frac{{\gamma }_{2k}}{N}\text{Tr}\left[{\left({\gamma }_{\omega }{\mathbf{A}}^T\mathbf{A}+{\gamma }_{2k}I\text{I}I\right)}^{-1}\right]\text{\hspace{1em}(24)}$$
类似于式（17），可以写出
$$\{\begin{array}{l}{\hat{\mathbf{x}}}_{2k}={\mathrm{g}\text{g}\mathrm{g}}_2({\mathbf{r}}_{2k},{\gamma }_{2k})\\ {\eta }_{2k}^{-1}={{\gamma }_{2k}}^{-1}<{\mathrm{g}\text{g}\mathrm{g}}_2^{\prime }({\mathbf{r}}_{2k},{\gamma }_{2k})>\end{array}\text{\hspace{1em}(25)}$$
第五步（消息传递）：类似于第三步，从变量节点${\mathbf{x}}_2$传递到因子节点$\delta$的消息为
$${\mu }_{{\mathbf{x}}_2\to \delta }({\mathbf{x}}_2)\propto \frac{\mathcal{N}({\mathbf{x}}_2;{\hat{\mathbf{x}}}_{2k},{\eta }_{2k}^{-1}I\text{I}I)}{\mathcal{N}({\mathbf{x}}_2;{\mathbf{r}}_{2k},{{\gamma }_{2k}}^{-1}\mathbf{I})}\text{\hspace{1em}(26)}$$
令${\mu }_{{\mathbf{x}}_2\to \delta }({\mathbf{x}}_2)=\mathcal{N}({\mathbf{x}}_2;{\mathbf{r}}_{1,k+1},{\gamma }_{1,k+1}^{-1}I\text{I}I)$，联合式（19）和式（26）可得
$$\{\begin{array}{l}{\mathbf{r}}_{1,k+1}=({\hat{\mathbf{x}}}_{2k}{\eta }_{2k}-{\mathbf{r}}_{2k}{\gamma }_{2k})/({\eta }_{2k}-{\gamma }_{2k})\\ {\gamma }_{1,k+1}^{}={\eta }_{2k}-{\gamma }_{2k}\end{array}\text{\hspace{1em}(27)}$$
而从因子节点$\delta$传递到变量节点${\mathbf{x}}_1$的消息与${\mu }_{{\mathbf{x}}_2\to \delta }({\mathbf{x}}_2)$是一致的。整个消息传递过程和信念估计操作依次迭代直至收敛。

总结：初始化因子节点$\delta$到变量节点${\mathbf{x}}_1$的消息后，首先计算变量节点${\mathbf{x}}_1$的估计信念；然后将消息传递至${\mathbf{x}}_2$，类似地计算变量节点${\mathbf{x}}_2$的估计信念，这样依次迭代直至收敛。

对矩阵$\mathbf{A}$做SVD分解，代入到Algorithm-3 （LMMSE Form）中，可以得到另一个等效的简化形式（尤其是简化了矩阵求逆！）：