AMP State Evolution的计算：以指数分布先验为例（AWGN）

最新推荐文章于 2024-06-26 20:22:05 发布

Turbo-shengsong

最新推荐文章于 2024-06-26 20:22:05 发布

阅读量882

点赞数 26

文章标签：概率论线性代数

本文链接：https://blog.csdn.net/weixin_43413559/article/details/136354424

版权

信号模型

对于AWGN模型:
$\tag{1}$

我们考虑

$x$ 的先验分布为伯努利-指数分布，即 $p(x)=(1-\rho) \cdot \delta(x) + \rho \cdot \lambda e^{- \lambda x} \mathbf 1_{x\geq0}$
$w$ 的分布为 $\sim \mathcal N(0, \tau^2)$

基于上述信息，我们可以计算 $X, Y$ 的联合分布
$\cdot p(y|x) = \left ( (1-\rho) \cdot \delta(x) + \rho \cdot \lambda e^{- \lambda x} \mathbf 1_{x\geq0} \right) \cdot \mathcal N(y-x; 0, \tau^2) \tag{2}$

进一步，可以计算Y的边际分布，令 $-\lambda \tau^2$
$\begin{aligned} p(y) &= \int p(x,y) dx \\ &= \int \left ( (1-\rho) \cdot \delta(x) + \rho \cdot \lambda e^{- \lambda x} \right) \cdot \mathcal N(y-x; 0, \tau^2) dx \\ &= (1-\rho) \int \delta(x) \mathcal N(y; x, \tau^2) \mathrm {d} x+ \rho \cdot \lambda \int_{0}^{\infty} e^{- \lambda x} \cdot \frac{1}{\sqrt{2 \pi \tau^2}} e^{ -\frac{(x-y)^2}{2 \tau^2} } \mathrm {d} x \\ & = (1- \rho) \mathcal N(y; 0, \tau^2) + \rho \cdot \lambda \cdot e^{ \frac{-2\lambda y+\lambda^2 \tau^2}{2 } } \int_{0}^{\infty} \frac{1}{\sqrt{2 \pi \tau^2}} e^{ - \frac{ \left( x - (y -\lambda \tau^2)\right)^2 }{ 2 \tau^2} } \mathrm {d} x \\ & = (1- \rho) \mathcal N(y; 0, \tau^2) + \rho \cdot \lambda \cdot e^{ \frac{-2\lambda y+\lambda^2 \tau^2}{2 } } \left( 1 - \Phi \left (-\frac{(y -\lambda \tau^2)}{\tau} \right) \right ) \\ &= (1- \rho) \mathcal N(y; 0, \tau^2) + \rho \lambda e^{-\frac{\lambda^2 \tau^2}{2}} \cdot e^{- \lambda m(y)} \left( 1 - \Phi \left (-\frac{m(y)}{\tau} \right) \right ) \end{aligned} \tag{3}$

若记
$\begin{aligned} \beta_0(y) &=(1- \rho) \mathcal N(y; 0, \tau^2) \\ \beta_1(y) &= c \cdot e^{- \lambda m(y)} \left( 1 - \Phi \left (-\frac{m(y)}{\tau} \right) \right ) \end{aligned}$

其中 $c=\rho \lambda e^{-\frac{\lambda^2 \tau^2}{2}}$ ，则 $=\beta_0(y) + c \cdot \beta_1(y)$ 。

后验均值和后验方差的推导

我们想要求后验均值 $\mathbb E[x|y]$ ，即
$\begin{aligned} \mathbb E[x|y] &= \frac{1}{p(y)} \int x \cdot p(x,y) \mathrm {d} x \\ &= \frac{1}{p(y)} \cdot \rho \cdot \lambda \cdot e^{ \frac{-2\lambda y+\lambda^2 \tau^2}{2 } } \int_{0}^{\infty} x \frac{1}{\sqrt{2 \pi \tau^2}} e^{ - \frac{ \left( x - (y -\lambda \tau^2)\right)^2 }{ 2 \tau^2} } \mathrm {d} x \\ & = \frac{1}{p(y)} \cdot \rho \cdot \lambda \cdot e^{ \frac{-2\lambda y+\lambda^2 \tau^2}{2 } } \cdot \left ( {1 - \Phi\left(\frac{-\left(y -\lambda \tau^2\right)}{\tau}\right)} \right ) \cdot \int_{0}^{\infty} x f(x;y -\lambda \tau^2, \tau, 0) \mathrm dx \\ &=\rho \lambda \cdot \frac{1}{p(y)} e^{ \frac{-2\lambda y+\lambda^2 \tau^2}{2 } } \cdot \left( {1 - \Phi\left(\frac{-\left(y -\lambda \tau^2\right)}{\tau}\right)} \right) \cdot \left \{ \left(y -\lambda \tau^2\right) + \tau \frac{\varphi\left(\frac{-\left(y -\lambda \tau^2\right)}{\tau}\right)}{1 - \Phi\left(\frac{-\left(y -\lambda \tau^2\right)}{\tau}\right)} \right \} \\ & = \frac{1}{p(y)} \cdot \rho \lambda e^{-\frac{\lambda^2 \tau^2}{2}} \cdot \left( {1 - \Phi\left(-\frac{m(y)}{\tau}\right)} \right) \cdot \left \{ m(y) e^{- \lambda m(y)} + \tau e^{- \lambda m(y)} \frac{\varphi\left(-\frac{m(y)}{\tau}\right)}{1 - \Phi\left(-\frac{m(y)}{\tau}\right)} \right \} \end{aligned} \tag{4}$

其中 $f$ 表示截断高斯分布，见附录-A，进一步我们计算后验二阶矩：
$\begin{aligned} \mathbb E[x^2|y] &= \frac{1}{p(y)} \int x^2 \cdot p(x,y) \mathrm {d} x \\ &= \frac{1}{p(y)} \cdot \rho \cdot \lambda \cdot e^{ \frac{-2\lambda y+\lambda^2 \tau^2}{2 } } \int_{0}^{\infty} x^2 \frac{1}{\sqrt{2 \pi \tau^2}} e^{ - \frac{ \left( x - (y -\lambda \tau^2)\right)^2 }{ 2 \tau^2} } \mathrm {d} x \\ & = \frac{1}{p(y)} \cdot \rho \cdot \lambda \cdot e^{ \frac{-2\lambda y+\lambda^2 \tau^2}{2 } } \cdot \left ( {1 - \Phi\left(\frac{-\left(y -\lambda \tau^2\right)}{\tau}\right)} \right ) \cdot \int_{0}^{\infty} x^2 f(x;y -\lambda \tau^2, \tau, 0) \mathrm dx \\ &= \frac{1}{p(y)} \cdot \rho \cdot \lambda \cdot e^{ \frac{-2\lambda y+\lambda^2 \tau^2}{2 } } \cdot \left ( {1 - \Phi\left(\frac{-\left(y -\lambda \tau^2\right)}{\tau}\right)} \right ) \cdot \left ( (y -\lambda \tau^2)^2 + \tau^2 + (y -\lambda \tau^2) \tau \frac{\varphi\left(\frac{-\left(y -\lambda \tau^2\right)}{\tau}\right)}{1 - \Phi\left(\frac{-\left(y -\lambda \tau^2\right)}{\tau}\right)} \right ) \\ &= \frac{1}{p(y)} \cdot \rho \lambda e^{-\frac{\lambda^2 \tau^2}{2}} \cdot \left( {1 - \Phi\left(-\frac{m(y)}{\tau}\right)} \right) \cdot \left ( m(y)^2 e^{- \lambda m(y)} + \tau^2 e^{- \lambda m(y)} + \tau m(y) e^{- \lambda m(y)} \cdot \frac{\varphi\left(-\frac{m(y)}{\tau}\right)}{1 - \Phi\left(-\frac{m(y)}{\tau}\right)} \right) \end{aligned} \tag{5}$

我们可以把(4,5)写为
$\begin{aligned} \mathbb E[x|y] &= c \frac{\beta_1(y)}{p(y)} \left \{ m(y) + \tau \frac{\varphi\left(-\frac{m(y)}{\tau}\right)}{1 - \Phi\left(-\frac{m(y)}{\tau}\right)} \right \} = c \frac{\beta_1(y)}{p(y)} t_1(y)\\ \mathbb E[x^2|y] &= c \frac{\beta_1(y)}{p(y)} \left \{ m(y)^2 + \tau^2 + \tau m(y) \cdot \frac{\varphi\left(-\frac{m(y)}{\tau}\right)}{1 - \Phi\left(-\frac{m(y)}{\tau}\right)} \right \} = c \frac{\beta_1(y)}{p(y)} t_2(y) \end{aligned}$

联合式(4)和式(5)，我们可以得到 $X ∣ Y$ 对应的后验方差，即
$\begin{aligned} \mathrm{var}[x|y] &= \mathbb E[x^2|y] - \mathbb E[x|y]^2 \\ \end{aligned}$

贝叶斯MMSE的计算和数值仿真

贝叶斯MMSE为
$\begin{aligned} mmse(\tau^2) &= \int \mathrm{var}[x|y] p(y) \mathrm d y \\ &=\int \frac{\beta_1(y)}{p(y)} \left \{ c t_2(y) - c^2 t_1^2(y) \right \} p(y) \mathrm d y \\ &=\int {\beta_1(y)} \left \{ c t_2(y) - c^2 \frac{\beta_1(y)}{p(y)} t_1^2(y) \right \} \mathrm d y \\ &= c \int {\beta_1(y)} t_2(y) \mathrm d y - c^2 \int \frac{\beta_1(y)}{p(y)} t_1^2(y) \mathrm d y \end{aligned}$

% basic parameters
rho = 0.2; lambda = 0.5; tau2 = 0.1;

normpdf = @(z) exp(-0.5 * z.^2) ./ sqrt(2 * pi);
normcdf = @(z) 0.5 * (1 + erf(z ./ sqrt(2)));

tau = sqrt(tau2);
mu_y = @(y) y - lambda * tau2;
alpha = @(y) -mu_y(y) ./ tau;

constant = rho * lambda * exp(-lambda^2 * tau2 / 2);

beta_1 = @(y) exp(-lambda * mu_y(y)) .* (1 - normcdf(alpha(y)));

p_y = @(y) (1-rho) .* normpdf(y./tau) ./ tau + ...
    rho .* lambda .* exp( (-2*lambda*y + lambda^2 * tau2) ./ 2 ) .* ...
    (1 - normcdf(alpha(y) ) );

t2_y = @(y) mu_y(y).^2 + tau2 + tau * mu_y(y) .* normpdf(alpha(y)) ./ (1-normcdf(alpha(y)));

t1_y = @(y) mu_y(y) + tau * normpdf(alpha(y)) ./ (1-normcdf(alpha(y)));

integral_1stTerm = @(y) beta_1(y) .* t2_y(y);
integral_2ndTerm = @(y) beta_1(y).^2 ./ p_y(y) .* t1_y(y).^2;

% find the beginning of integration
% if the beginning start from -inf, it suffers from numerical problem..
% as the mse is too small for MATLAB.
step = 0;
step_size = 0.01;
while true
    if constant^2 * integral_2ndTerm(step) < 1e-8
        lim_start = step ;
        break
    elseif step < -100
        lim_start = -100;
        break;
    else
        step = step - step_size;
    end 
end

%lim_start,
mse_1stTerm = constant * integral(integral_1stTerm, lim_start, 60);

mse_2ndTerm = constant^2 * integral(integral_2ndTerm, lim_start, 60);

bayesianMSE = mse_1stTerm - mse_2ndTerm;

验证

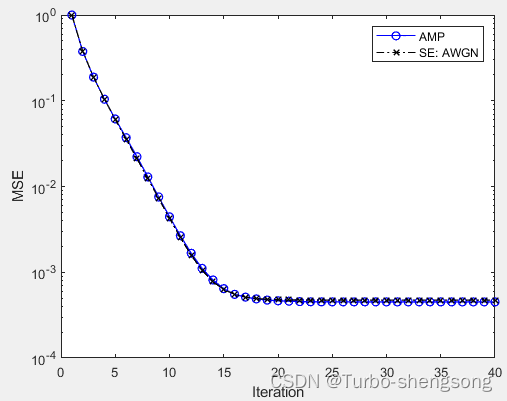
利用AMP算法与State evolution在MSE上的一致性，在大系统极限下，如果经过AMP得到的MSE与经过State evolution得到的MSE一致，那么认为结论是争取的。

截断高斯分布

假设 $\sim \mathcal N(\mu, \sigma^2)$ ，高斯分布在 $\infty)$ 处截断，那么阶段高斯的分布可以写为：
$f(x;\mu,\sigma,a) = \frac{1}{\sigma} \frac{ \varphi \left ( \frac{x-\mu}{\sigma} \right) }{1 - \Phi \left( \frac{a-\mu}{\sigma} \right)}$
其中
$\varphi(\xi) = \frac{1}{\sqrt{2 \pi}} e^{ -\frac{1}{2} \xi^2 }$

令 $\alpha=\frac{a-\mu}{\sigma}$ ， $Z=1-\Phi(\alpha)$ ，则我们可以得到均值和方差
$\begin{aligned} \mathbb E_f[x] &= \mu + \sigma \frac{\varphi(\alpha)}{Z} \\ \mathrm var_f[x] &= \sigma^2 \left ( 1 + \frac{\alpha \varphi(\alpha)}{Z} - \left( \frac{\varphi(\alpha)}{Z} \right)^2 \right) \end{aligned}$

借此，我们可以得到二阶矩为
$\begin{aligned} \mathbb E_f[x^2] &= \mathbb E_f[x]^2 + \mathrm var_f[x] \\ &= \left( \mu + \sigma \frac{\varphi(\alpha)}{Z} \right)^2 + \sigma^2 \left ( 1 + \frac{\alpha \varphi(\alpha)}{Z} - \left( \frac{\varphi(\alpha)}{Z} \right)^2 \right) \\ &= \mu^2 + \sigma^2 + (2 \mu \sigma + \alpha \sigma^2) \frac{\varphi(\alpha)}{Z} \\ &= \mu^2 + \sigma^2 + \sigma(\mu + a ) \frac{\varphi(\alpha)}{Z} \end{aligned}$