林轩田《机器学习基石》（六）—— Theory of generalization

最新推荐文章于 2021-03-08 12:40:37 发布

不抱我起来就没法医治

最新推荐文章于 2021-03-08 12:40:37 发布

阅读量308

点赞数 1

分类专栏：机器学习基石文章标签：人工智能

本文链接：https://blog.csdn.net/weixin_43463276/article/details/107416449

版权

机器学习基石专栏收录该内容

16 篇文章 4 订阅

订阅专栏

之前我们假设了M为有限个的时候，机器学习可以进行。上一节课我们讨论了M是无限个的时候，我们定义了一个成长函数 $m_H(N)$ ，即dichotomy的最大个数。可以看到，当 $m_H(N)$ 是多项式，那么不等式会表现好，如果是指数则表现不一定会好。又提到，如果存在一个break point时， $m_H(N)$ 可能会越来越远离2^N，而这就是我们所希望的。

一、回顾

我们首先回顾一下上一次讲的内容，即四种成长函数与break point的关系：

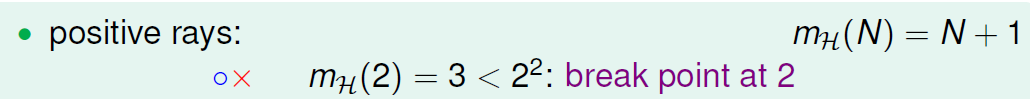
相当于对一维数轴的N个点进行分类，

如图，只有阈值的正方向被分类为正。

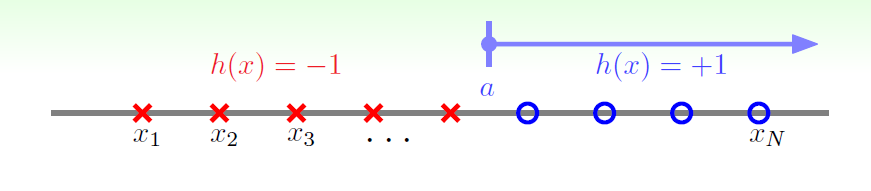
所以，它没法分‘x o’这样的数据，所以在break point 在2.

————————————————————————————————————————————————

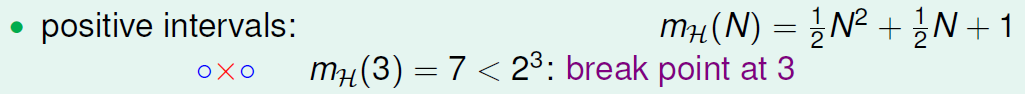
相当于h是一个区间，这个区间内含着的点被分类为正。

所以，它没法分‘o x o’这样的数据，所以在break point 在3.

————————————————————————————————————————————————

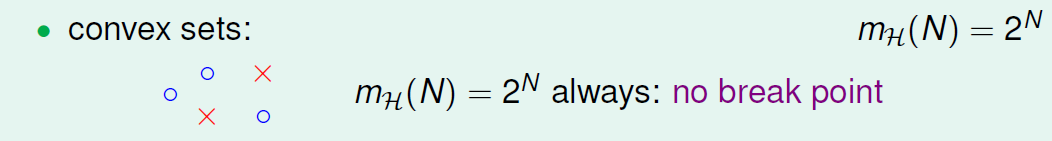
相当于h是一个凸集，当在凸集内时，点被分类为正。

由于成长函数是dichotomy的最大个数。所以我们看如何分布数据才有可能找到dichotomy的最大个数，为了使得点两两间不受影响，所以我们使得数据集D按照如下的凸分布，即所有的数据点围成一个圆圈，

可以看到只要我们把所有的正点连起来，就可以正确分类，显然没有没办法分的情况，所有情况都可以分，即 $m_H =2^N$ 。这种情况下，N个点所有可能的分类情况都能够被hypotheses set覆盖，我们把这种情形称为shattered。通俗来讲shattered就是： $m_H =2^N$ 。

————————————————————————————————————————————————

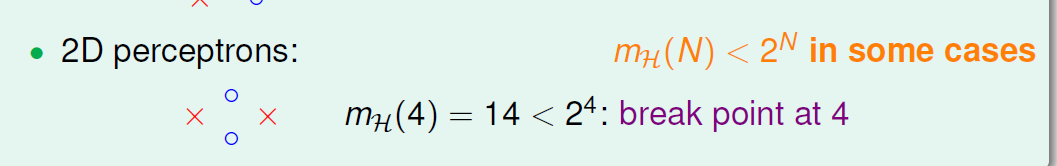
2D感知是指用一条直线分割两类的点。直线的一面被分类为正，另一面被分类为负，可以看到在左下角这种情况时候，不能仅用一条直线就完美分类，所以break point在4。

————————————————————————————————————————————————

二、B(N, K)：成长函数的上限

如果我们已知break point，那我们能否知道他的成长函数是多少或者最大可能是多少呢？

我们来看一个例子，如果我们已知break point在2，即k=2，

那么我们肯定可以知道

N=1, $m_H =2$ ,

N=2, $m_H$ 最大是3（意味着不会shatter 任意两个点）

那么N=3时会怎么样呢？

先看如果h只有一种时候的情况，就是仅把他们都分类为正。那么此时不会shatter 任意两个点。

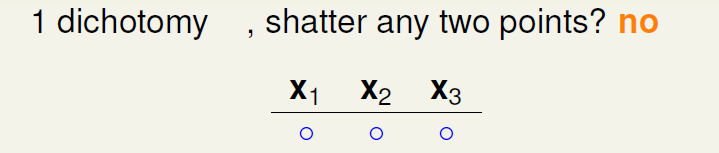
我们增加h的种类，使得它不会使得点全分类为正，还有别的分类‘’o o x。此时也不会shatter 任意两个点。

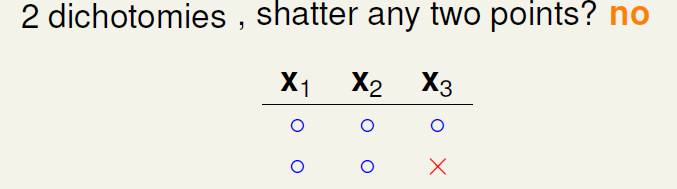
继续增加h的种类，新增分类‘’o x o。此时也不会shatter 任意两个点。

继续增加h的种类，新增分类‘’o x x。此时x2和x3被shattered。

所以上面的那种分类不能算，我们看其他新增的，新增分类‘x o o’，此时不会shatter 任意两个点

继续增加h的种类，新增分类‘’x o x。此时x1和x3被shattered。

继续这样试下去....

可以发现，当N=3时， $m_H$ 最大是4，4远小于2^3。可以看到，只要出现一个break point，那么对未来的成长函数会产生一个限制。

我们的一个想法是：

我们想知道在break point之后的点的 $m_H$ 的上限是多少，我们定义一个上限函数B(N, K)，而且，当我们知道break point K=？可以推出 $m_H(K)< 2^K$ ，从而可以知道B(N, K)，一个麻烦的方法是穷举法。

我们先说说找到B(N, K)的好处：在将来，我们只需要看break point在多少就行了，而不用看具体的h是多少，通俗一点的解释是，例如2D感知和正区间的break point都在3，但现在我们不管h究竟是什么函数，是2D感知还是正区间，只需要明白break point一样，我们按一种类型进行研究。

那么究竟如何确定B(N, K)呢？

我们先看一些已知的情况。

比如刚才提到的B(2, 2)=3，B(3, 2)=4，以及显然的B(N, 1)=1.

值得注意的是B(N, K)只是 $m_H$ 一个上限，实际的 $m_H$ 可能会小。

三、B(N, K)的上限：成长函数上限的上限是多少？

以B(4,3)为例，首先想着能否构建B(4,3)与B(3,x)之间的关系。

我们先用穷举法看一下，B(4,3)=11

首先关注x4，它有两种样子：

橙色：成双成对，即其他三个点一样的情况下，‘o’，‘x’都有，记为 $\alpha$ 个

紫色：只有单个的，记为 $\beta$ 个

$B(4,3)=11=2\alpha +\beta$ ，我们再看下面这张图，由于我们知道k=3，所以任意三个点，比如现在的x1，x2，x3不会shatter，所以得到 $\alpha +\beta \leq B(3,3)$

我们拿出橙色的部分，可以看到x4已经都成双成对了，所以如果x1，x2，x3中某两个点shatter，即两个点也是成双成对，那么这两个点和x4的组合就会成为3个点的shatter（与已知矛盾，所以x1，x2，x3中不会有两个点shatter）。

因此橙色的个数 $\alpha \leq B(3,2)$ 。

可以得到：

以及进一步

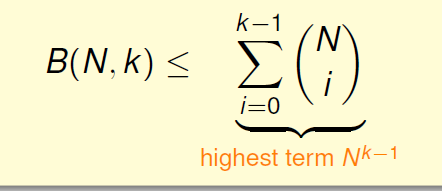
可以看到B(N,k)的上界是N^(k-1)。所以 $m_H$ 会被B(N,k) bound住，B(N,k)会被一个N的多项式poly（N）bound住。其实这里就是给了一个B(N, K)上限的上限，上述的小于等于号可以被证明为等号。（视频没有详细解答）

四、理论部分

由上面可能知道，不等式中的成长函数可能是多项式一样的，那么我们能否直接将 $m_H(N)$ 带入到原不等式呢？就像下面这样：

但我们实际上的结果不是上述那样的，是一个差不多的版本：

课程不具体讲述他的每一步数学细节，而是大概提供一个思路。

主要有三个步骤：

1.用 $E_{in'}$ 代替 $E_{out}$

在原来的式子中，因为样本的个数是有限的，所以可以h的所有种类， $E_{in}$ 是有限个的，但是在空间中样本无限，而且直线稍微变一下角度就是不同的h，所以 $E_{out}$ 有无限个。

那么如何让 $E_{out}$ 有限呢？除非点有限，所以我们可以拿不同于原资料D的新资料D‘（D‘中也是有N个点），来计算 $E_{in'}$ 去估计 $E_{out}$ 。也就是说 $E_{in'}$ 使用D‘估计出的值。

我们可以得到一个结论：如果今天有BAD发生（ $E_{in}$ 和 $E_{out}$ 很远），那么大概率 $E_{in}$ 和 $E_{in'}$ 也会很远（一种新BAD）。所以我们可以将原来的BAD换成新的一种BAD。

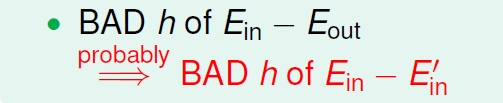
所以我们可以获得：

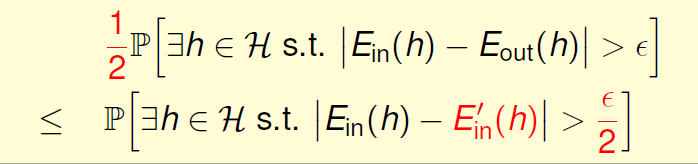
左边这个1/2是因为：上述事情是“大概率”的，所以肯定大于1/2。而且右边更严格了，因为我们希望 $E_{in}$ 和 $E_{in'}$ 更严格一点。

2.按类别分解H

我们这边在乎的是BAD，如果我hypothesis set在D和D'上作出一样的dichotomy，那么今天他的 $E_{in}$ 和 $E_{in'}$ 都会长得一样，所以我们只要知道：

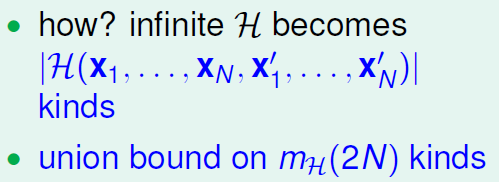
用下图直观的解释一下我们所做的事情：

图一是所有dataset，红色表示发生错误的概率只有红色部分，但是图二是使用union bound（这会使得放缩太大）发现发生BAD的几率占据了整个平面，但现在其实我们知道他是有交集的，实际情况是图三那样的。以下是我个人的理解：所以现在我们不用在全平面找BAD了，可以用D和D‘中的2N个点来固定hypothesis set了。

3.固定hypothesis set

这是我们使用抽样D'时候的情况，我们现在要看抽样一次和抽样所有取平均有什么差别。比如抽D'和抽D+D'（2N个）的平均：

因此我们引入成长函数，得到了一个新的不等式，称为Vapnik-Chervonenkis(VC) bound：

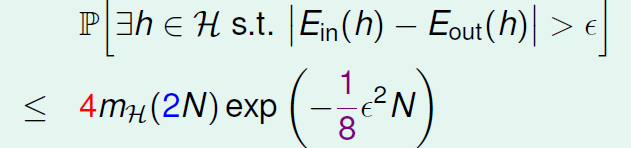
可以看到这个 bound用了很多近似，既然不是那么准，为什么大量时间研究呢？（以后会讲）

总结

不抱我起来就没法医治

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
林轩田《机器学习基石》（六）—— Theory of generalization

之前我们假设了M为有限个的时候，机器学习可以进行。上一节课我们讨论了M是无限个的时候，我们定义了一个成长函数，即dichotomy的最大个数。可以看到，当是多项式，那么不等式会表现好，如果是指数则表现不一定会好。又提到，如果存在一个breakpoint时，可能会越来越远离2^N，而这就是我们所希望的。一、回顾我们首先回顾一下上一次讲的内容，即四种成长函数与break point的关系：相当于对一维数轴的N个点进行分类，如图，只有阈值的正方向被分类为正。所以，它没法分‘x o’这.
复制链接

扫一扫