1.Introduction
本系列将“https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python”的内容进行整理。
下面这个图是kalman filter 的核心思想,结合系统自身的动力学特性做预测,再结合传感器的数据,进行更新。

变量解释:
| Column 1 | Column 2 |
|---|---|
| x | 状态真实值 |
| x ^ \hat{x} x^ | 状态的estimate (posterior) |
| x ‾ \overline{x} x | 状态的预测值 (prior) |
| z k z_k zk | 传感器的数值 (measurement) |
2. gh filter
- prediction
x ‾ = x ^ + v ^ ∗ d t v ‾ = v ^ (2.1) \begin{aligned} \overline{x} &=\hat{x}+\hat{v}*dt \\ \overline{v} & =\hat{v} \end{aligned} \tag{2.1} xv=x^+v^∗dt=v^(2.1) - update
x和v的更新,都可以用下面这个图表示。

x ^ = x ‾ + g ( z k − x ‾ ) v ^ = v ‾ + h ( z k − x ^ ) Δ t (2.2) \begin{aligned} \hat{x} &=\overline{x}+g(z_k-\overline{x}) & \\ \hat{v} & = \overline{v}+h\frac{(z_k-\hat{x})}{\Delta{t}} \end{aligned} \tag{2.2} x^v^=x+g(zk−x)=v+hΔt(zk−x^)(2.2)
g和h的取值范围是[0,1]代表着我们对测量数据的相信程度,越相信测量数据,则g和h越大。
3. 离散贝叶斯滤波器
离散贝叶斯滤波器同样遵循gh filter 的框架。
- prediction
作者以tracking dog为例,假设狗当前位置的概率分布为左图,狗在接下来1s内可能跑0m,1m,2m对应的离散概率分布为[0.1,0.8,0.1]。预测狗接下来的位置为右图。可以用卷积的方式表达。卷积之后的效果是,概率更加发散,所以prediction以后往往不确定性会提高。
x k ‾ = x k ^ ∗ f x ( ⋅ ) (3.1) \overline{x_k}=\hat{x_k}*f_x(\cdot) \tag{3.1} xk=xk^∗fx(⋅)(3.1)

- update
为了体现离散概率的特点,在tracking dog这个例子中,使用的位置传感器,不能直接给出位置,但是能判断狗当前是在门前还是墙前。传感器正确的概率0.75。根据传感器返回的结果 z k z_k zk更新狗的位置的概率分布。
P ( x ^ ∣ z ) = P ( z ∣ x ‾ ) P ( x ‾ ) P ( z ) (3.2) P(\hat{x}|z)=\frac{P(z|\overline{x})P(\overline{x})}{P(z)} \tag{3.2} P(x^∣z)=P(z)P(z∣x)P(x)(3.2)
这个公式代表这
p o s t e r i o r = l i k e l i h o o d ∗ p r i o r n o r m a l i z a t i o n (3.3) posterior=\frac{likelihood*prior}{normalization} \tag{3.3} posterior=normalizationlikelihood∗prior(3.3)
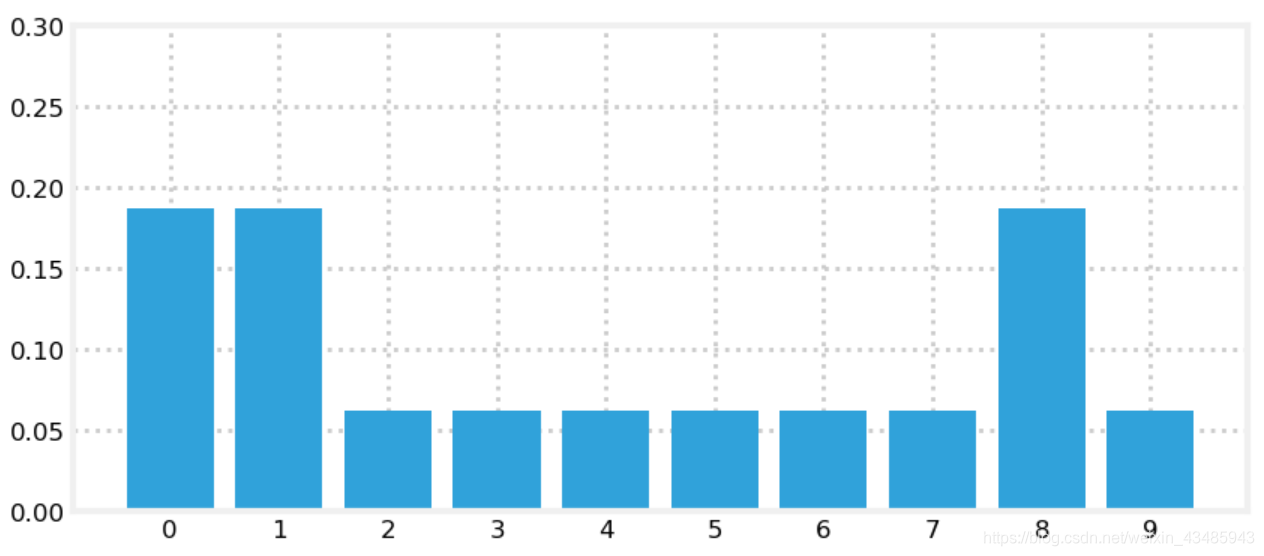
假设有10个离散的位置点,狗一开始随机在一个位置,位置的map用向量表示为[1,1,0,0,0,0,0,0,1,0] (1表示门,0表示墙),每个位置点的概率是0.1*ones[10,1],然后传感器给出了狗在门前,更新之后狗所处位置的概率如下图。因而测量数据能降低不确定性。
4. 卡尔曼滤波
4.1 单变量卡尔曼滤波
4.1.1 卡尔曼滤波和离散贝叶斯滤波的联系
离散贝叶斯滤波有几个重要的缺陷
- 没办法计算多变量
- 计算太复杂,需要独立的计算每个离散点位置点的概率
- 可能会有多个结果,如果出现多个点的概率是一样的,就出现了多个结果
在实际生活中,每个点的概率很可能遵循一定的概率分布,其中常见的概率分布是正态分布,所以单变量卡尔曼滤波将离散贝叶斯中的每个点的概率用正态分布表示。
4.1.2 predict 和 update
- predict
x ‾ = x ^ + f ( x ) \overline{x}=\hat{x}+f(x) x=x^+f(x),其中 f ( x ) f(x) f(x)均值和方差分别为 μ \mu μ和 σ 2 \sigma^2 σ2,因为两个正态分布的期望和方差之和的满足下面的关系。
x ‾ = x ^ + μ f ( x ) σ x ‾ 2 = σ ^ 2 + σ f ( x ) 2 (4.1) \begin{aligned} \overline{x} &=\hat{x}+\mu_{f(x)} \\ \overline{\sigma_{x}}^2 & = \hat{\sigma}^2+\sigma_{f(x)}^2 \end{aligned} \tag{4.1} xσx2=x^+μf(x)=σ^2+σf(x)2(4.1) - update
计算update,按照贝叶斯公式(3.2),只能按照正态分布的公式去计算所需要的结果。
P ( z k ∣ x k ^ ) = 1 2 π σ z 2 exp ( − ( x − u z ) 2 2 σ z 2 ) P ( x k ^ ) = 1 2 π σ x 2 exp ( − ( x − u x ) 2 2 σ x 2 ) (4.2) \begin{aligned} P(z_k|\hat{x_k}) & =\frac{1}{\sqrt{2\pi\sigma_z^2}}\exp(-\frac{(x-u_z)^2}{2\sigma_z^2}) \\ P(\hat{x_k}) & = \frac{1}{\sqrt{2\pi\sigma_x^2}}\exp(-\frac{(x-u_x)^2}{2\sigma_x^2}) \end{aligned} \tag{4.2} P(zk∣xk^)P(xk^)=2πσz21exp(−2σz2(x−uz)2)=2πσx21exp(−2σx2(x−ux)2)(4.2)
因为 P ( z k ∣ x k ^ ) P ( x k ^ ) P(z_k|\hat{x_k}) P(\hat{x_k}) P(zk∣xk^)P(xk^)的结果经过normalization之后仍然是正态分布。
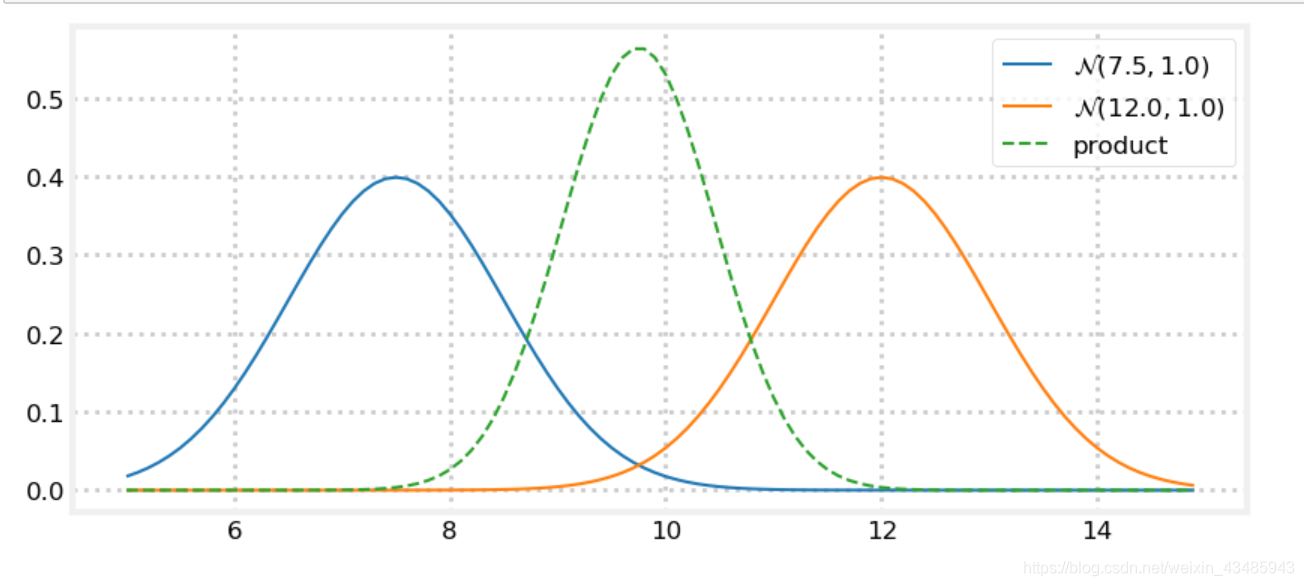
P ( x k ^ ∣ z k ) ∝ P ( z k ∣ x k ‾ ) P ( x k ‾ ) ∝ 1 2 π σ x 2 exp ( − ( x − u x ) 2 2 σ x 2 ) ∝ exp ( − x 2 ( σ z 2 + σ x 2 ) − 2 x ( μ z σ x 2 + μ x σ z 2 ) 2 σ z 2 σ x 2 ) ∝ exp ( − x − μ x σ z 2 + μ z σ x 2 σ z 2 + σ x 2 σ x 2 σ z 2 σ x 2 + σ y 2 ) (4.3) \begin{aligned} P(\hat{x_k}|z_k) & \propto P(z_k|\overline{x_k}) P(\overline{x_k}) \\ & \propto \frac{1}{\sqrt{2\pi\sigma_x^2}}\exp(-\frac{(x-u_x)^2}{2\sigma_x^2}) \\ & \propto \exp(-\frac{x^2(\sigma_z^2+\sigma_x^2)-2x(\mu_z\sigma_x^2+\mu_x\sigma_z^2)}{2\sigma_{z}^2\sigma_{x}^2}) \\ & \propto \exp(-\frac{x-\frac{\mu_x\sigma_z^2+\mu_z\sigma_x^2}{\sigma_z^2+\sigma_x^2}} {\frac{\sigma_x^2\sigma_z^2}{\sigma_x^2+\sigma_y^2}}) \end{aligned} \tag{4.3} P(xk^∣zk)∝P(zk∣xk)P(xk)∝2πσx21exp(−2σx2(x−ux)2)∝exp(−2σz2σx2x2(σz2+σx2)−2x(μzσx2+μxσz2))∝exp(−σx2+σy2σx2σz2x−σz2+σx2μxσz2+μzσx2)(4.3)
根据公式(4.3)可以推导出结合测量结果更新后的数据的期望和方差为
x ^ = μ z σ x ‾ 2 + μ x ‾ σ z 2 σ x ‾ 2 + σ z 2 σ x ^ 2 = σ x ‾ 2 σ z 2 σ x ‾ 2 + σ z 2 (4.4) \begin{aligned} \hat{x} &=\frac{\mu_z\sigma_{\overline{x}}^2+\mu_{\overline{x}}\sigma_z^2} {\sigma_{\overline{x}}^2+\sigma_z^2} \\ \sigma_{\hat{x}}^2 & = \frac{\sigma_{\overline{x}}^2\sigma_z^2}{\sigma_{\overline{x}}^2+\sigma_z^2} \end{aligned} \tag{4.4} x^σx^2=σx2+σz2μzσx2+μxσz2=σx2+σz2σx2σz2(4.4)
4.1.3 单变量卡尔曼滤波和gh滤波的联系
在gh滤波中,我们知道gh表示对测量数据的信任程度(范围是[0,1])。
在单变量卡尔曼滤波中,令
g
=
σ
x
‾
2
σ
x
‾
2
+
σ
z
2
(4.5)
g=\frac{\sigma_{\overline{x}}^2}{\sigma_{\overline{x}}^2+\sigma_z^2} \tag{4.5}
g=σx2+σz2σx2(4.5)
update过程可以改写成:
x
^
=
μ
x
‾
+
g
(
μ
z
−
μ
x
‾
)
σ
x
^
2
=
g
σ
z
2
=
(
1
−
g
)
σ
x
‾
2
(4.6)
\begin{aligned} \hat{x} &=\mu_{\overline{x}}+g(\mu_z-\mu_{\overline{x}}) \\ \sigma_{\hat{x}}^2 & = g\sigma_z^2=(1-g)\sigma_{\overline{x}}^2 \end{aligned} \tag{4.6}
x^σx^2=μx+g(μz−μx)=gσz2=(1−g)σx2(4.6)
我
们
能
观
察
到
这
里
只
有
参
数
g
,
并
没
有
出
现
了
h
?
\color{red}{我们能观察到这里只有参数g,并没有出现了h?}
我们能观察到这里只有参数g,并没有出现了h?
在单变量卡尔曼滤波中,v只能来源于自身的命令输入u,或者是其他的测速传感器。
4.1.4 单变量卡尔曼滤波和互补滤波器
互补滤波器的结构如下
- predict
x k ‾ = x k ^ + f ( x ) Δ t (4.7) \overline{x_k}=\hat{x_k}+f(x)\Delta t \tag{4.7} xk=xk^+f(x)Δt(4.7) - update
x ^ k + 1 = 0.98 ∗ x k ‾ + 0.02 ∗ z k = x k ‾ + 0.02 ( z k − x k ‾ ) (4.8) \begin{aligned} \hat{x}_{k+1} &=0.98*\overline{x_k}+0.02*z_k \\ & =\overline{x_k}+0.02(z_k-\overline{x_k}) \end{aligned} \tag{4.8} x^k+1=0.98∗xk+0.02∗zk=xk+0.02(zk−xk)(4.8)
可以发现互补滤波器本质上就是一个最简单的gh 滤波。 - 低通滤波特性
因为在互补滤波器中存在延时环节 z z − 0.98 \frac{z}{z-0.98} z−0.98z,可以推广到所有的gh架构的滤波器都具有一定的低通滤波的功能,从这个角度来看,卡尔曼滤波本身也有一定的滤波的作用(经过measurement之后方差减小了,效果类似低通滤波)
r o l l = ( 0.02 ∗ z k + 0.98 ∗ f ( x ) Δ t ) z z − 0.98 (4.9) roll=(0.02*z_k+0.98*f(x)\Delta t)\frac{z}{z-0.98} \tag{4.9} roll=(0.02∗zk+0.98∗f(x)Δt)z−0.98z(4.9)

图片来源于[2]
4.1.5 单变量卡尔曼滤波的缺陷
最重要的实际上我们知道 ( x , x ˙ ) (x,\dot{x}) (x,x˙)是有很大的相关性,但是在单变量卡尔曼滤波中,变量 x ˙ \dot{x} x˙的特性并没有利用上,和x之间的联系也没有用上。
4.2 多变量卡尔曼滤波
4.2.1 多变量正态分布
因为多变量之间存在一定的联系,所以多变量的采用协方差的方式进行定义。
例如身高和体重(W,H)是一对正相关的变量
Σ
=
[
σ
H
2
σ
H
W
σ
W
H
σ
W
2
]
(4.10)
\Sigma= \begin{bmatrix} \sigma_H^2 & \sigma_{HW} \\ \sigma_{WH} & \sigma_W^2 \end{bmatrix} \tag{4.10}
Σ=[σH2σWHσHWσW2](4.10)
正态分布的数学表达式为:
f
(
x
,
u
,
Σ
)
=
1
(
2
π
)
n
Σ
exp
(
−
1
2
(
x
−
u
)
T
Σ
(
x
−
u
)
)
(4.11)
f(x,u,\Sigma)=\frac{1}{\sqrt{(2\pi)^n\Sigma}} \exp(-\frac{1}{2}(x-u)^T\Sigma(x-u)) \tag{4.11}
f(x,u,Σ)=(2π)nΣ1exp(−21(x−u)TΣ(x−u))(4.11)
同样的需要计算两个多变量高斯分布的product和相加,在我们展开计算之前,尝试从几何的角度理解,product 和相加的影响,这里以二维正态分布为例。
对于标准的高斯分布,有65%的数据落在
[
u
−
σ
,
u
+
σ
]
[u-\sigma, u+\sigma]
[u−σ,u+σ], 有95%的数据落在
[
u
−
2
σ
,
u
+
2
σ
]
[u-2\sigma, u+2\sigma]
[u−2σ,u+2σ],有99.7%的数据落在
[
u
−
3
σ
,
u
+
3
σ
]
[u-3\sigma, u+3\sigma]
[u−3σ,u+3σ]。以
3
σ
3\sigma
3σ为范围表示正态分布的数据,如下图。

- 高斯分布的product
下面第一个图时协方差为0的二维高斯分布和协方差不为0的二维高斯分布的product,其结果的方差更小。下面第二个图是两个协方差不为0的高斯分布的product结果非常理想。


对于两个两个相关的变量,在测量过程中,虽然仅仅位置可以被直接观察到,速度是hidden variable,但是只要他们之间存在着线性关系,位置和速度都会变得非常精确。

接 下 来 需 要 非 常 关 注 , 如 何 只 观 察 位 置 , 得 到 更 加 精 确 的 位 置 和 速 度 ? \color{red}{接下来需要非常关注,如何只观察位置,得到更加精确的位置和速度?} 接下来需要非常关注,如何只观察位置,得到更加精确的位置和速度?
关于具体的高斯分布相加和product的公式,采用类比的方式进行理解 - 高斯分布相加

- 高斯分布product

4.2.2 线性动力学模型
考虑的模型噪声的线性动力学模型,可以表示为:
X
˙
=
A
X
+
B
U
+
w
(4.12)
\dot{X}=AX+BU+w \tag{4.12}
X˙=AX+BU+w(4.12)
在时不变系统中,可以表示为
X
(
t
k
+
1
)
=
F
(
Δ
t
)
X
t
k
+
B
(
t
k
)
U
(
t
k
)
+
w
(4.13)
X(t_{k+1})=F(\Delta t)X{t_k}+B(t_k)U(t_k)+w \tag{4.13}
X(tk+1)=F(Δt)Xtk+B(tk)U(tk)+w(4.13)
问题是如何将A转换成
F
(
Δ
t
)
F(\Delta t)
F(Δt),在无外部干扰的情况进行分析,根据欧拉法
X
=
exp
(
A
t
)
X
0
(4.14)
X=\exp(At)X_0 \tag{4.14}
X=exp(At)X0(4.14)
exp
(
A
t
)
\exp(At)
exp(At)通过泰勒展开可以得到:
exp
(
A
t
)
=
I
+
A
t
+
(
A
t
)
2
2
!
+
(
A
t
)
3
3
!
+
o
(
A
t
)
3
(4.15)
\exp(At)=I+ At + \frac{(At)^2}{2!}+ \frac{(At)^3}{3!} + o(At)^3 \tag{4.15}
exp(At)=I+At+2!(At)2+3!(At)3+o(At)3(4.15)
我们在使用的时候根据模型的阶数,选择
exp
(
A
t
)
\exp(At)
exp(At)需要精确的位数
- 一阶系统
x
(
t
k
+
1
)
=
x
˙
(
t
k
)
Δ
t
+
x
(
t
k
)
x(t_{k+1})=\dot{x}(t_k)\Delta t+x(t_k)
x(tk+1)=x˙(tk)Δt+x(tk)
改写成标准形式为:
[ x ˙ x ¨ ] = [ 0 1 0 0 ] [ x x ˙ ] (4.16) \begin{bmatrix} \dot{x} \\ \ddot{x} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \end{bmatrix} \tag{4.16} [x˙x¨]=[0010][xx˙](4.16)
则有
A = [ 0 1 0 0 ] (4.17) A = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \tag{4.17} A=[0010](4.17)
这里精确到 exp ( A t ) \exp(At) exp(At)的一阶倒数
F ( t k ) = I + A Δ t = [ 1 Δ t 0 1 ] (4.18) F(t_k)= I+A\Delta t = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix} \tag{4.18} F(tk)=I+AΔt=[10Δt1](4.18) - 二阶系统
x
(
t
k
+
1
)
=
0.5
x
¨
(
Δ
t
)
2
+
x
˙
(
t
k
)
Δ
t
+
x
(
t
k
)
x(t_{k+1})=0.5\ddot{x} (\Delta t)^2 + \dot{x}(t_k)\Delta t+x(t_k)
x(tk+1)=0.5x¨(Δt)2+x˙(tk)Δt+x(tk)
简化成标准形式:
[ x ˙ x ¨ x ¨ ′ ] = [ 0 1 0 0 0 1 0 0 0 ] [ x x ˙ x ¨ ] (4.19) \begin{bmatrix} \dot{x} \\ \ddot{x} \\ \ddot{x}' \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \\ \ddot{x} \end{bmatrix} \tag{4.19} ⎣⎡x˙x¨x¨′⎦⎤=⎣⎡000100010⎦⎤⎣⎡xx˙x¨⎦⎤(4.19)
则有:
A = [ 0 1 0 0 0 1 0 0 0 ] (4.20) A = \begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \tag{4.20} A=⎣⎡000100010⎦⎤(4.20)
这里精确到 exp ( A t ) \exp(At) exp(At)的二阶倒数
F ( t k ) = I + A Δ t + ( A Δ t ) 2 2 ! = [ 1 Δ t 0.5 ( Δ t ) 2 0 1 Δ t 0 0 1 ] (4.21) F(t_k)= I+A\Delta t + \frac{(A\Delta t)^2}{2!}= \begin{bmatrix} 1 & \Delta t & 0.5(\Delta t)^2\\ 0 & 1 & \Delta t \\ 0 & 0 & 1 \end{bmatrix} \tag{4.21} F(tk)=I+AΔt+2!(AΔt)2=⎣⎡100Δt100.5(Δt)2Δt1⎦⎤(4.21)
4.2.3 多变量卡尔曼滤波
- predict
期望是按照线性动力学公式推导过来的,没有什么好说的。
方差可以从1维的角度进行类比
Σ [ x ‾ ] 2 = E [ ( F x − F μ ) 2 ] = E [ F ( x − u ) 2 F T ] = E [ F Σ Σ T F T ] = F P F T (4.22) \begin{aligned} \Sigma[\overline{x}]^2 & = E[(Fx-F\mu)^2] \\ & = E[F(x-u)^2F^T] \\ & =E[F\Sigma \Sigma^TF^T] \\ & =FPF^T \end{aligned} \tag{4.22} Σ[x]2=E[(Fx−Fμ)2]=E[F(x−u)2FT]=E[FΣΣTFT]=FPFT(4.22)
对于Q,有两种主要的处理方式。
1)piecewise noise model: 以一阶系统为例,那么输入噪声w只对最高阶次(加速度)有影响,系统输入的噪声w对状态的影响可以表示为以下,
[ x x ˙ x ¨ ] = [ 1 Δ t 0.5 ( Δ t ) 2 0 1 Δ t 0 0 1 ] [ 0 0 1 ] w = [ 0.5 ( Δ t ) 2 Δ t 1 ] w = Γ w (4.23) \begin{bmatrix} x \\ \dot{x} \\ \ddot{x} \end{bmatrix} = \begin{bmatrix} 1 & \Delta t & 0.5(\Delta t)^2\\ 0 & 1 & \Delta t \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} w = \begin{bmatrix} 0.5(\Delta t)^2 \\ \Delta t \\ 1 \end{bmatrix} w = \Gamma w \tag{4.23} ⎣⎡xx˙x¨⎦⎤=⎣⎡100Δt100.5(Δt)2Δt1⎦⎤⎣⎡001⎦⎤w=⎣⎡0.5(Δt)2Δt1⎦⎤w=Γw(4.23)
那么w对状态变量 [ x , x ˙ ] [x, \dot{x}] [x,x˙]的影响可以表示为:
[ x x ˙ ] = Γ w = [ 0.5 ( Δ t ) 2 Δ t ] w \begin{bmatrix} x \\ \dot{x} \end{bmatrix} = \Gamma w = \begin{bmatrix} 0.5(\Delta t)^2 \\ \Delta t \end{bmatrix} w [xx˙]=Γw=[0.5(Δt)2Δt]w
可以计算Q为
Q = E [ Γ w w T Γ T ] = Γ σ v 2 Γ T (4..24) Q = E[\Gamma w w^T\Gamma^T]=\Gamma \sigma_v^2\Gamma^T \tag{4..24} Q=E[ΓwwTΓT]=Γσv2ΓT(4..24)
在计算二阶系统的时候,也可以采用同样的方式,认为w作为在最高阶变量(jerk)上,这样太复杂,没有必要,一般用:
Γ = [ 0.5 ( Δ t ) 2 Δ t 1 ] \Gamma= \begin{bmatrix} 0.5(\Delta t)^2 \\ \Delta t \\ 1 \end{bmatrix} Γ=⎣⎡0.5(Δt)2Δt1⎦⎤
2)simplific form 上面这种方法比较发杂,以二阶系统为例,在工程里,有时候也直接将Q简化的表示成:
Q = [ 0 0 0 0 0 0 0 0 σ v 2 ] Q = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & \sigma_v^2 \end{bmatrix} Q=⎣⎡00000000σv2⎦⎤
σ v 的 选 择 为 [ 0.5 Δ a , Δ a ] , 其 中 Δ a 是 单 个 采 样 周 期 内 加 速 度 最 大 变 化 值 \color{red}{\sigma_v的选择为[0.5\Delta a, \Delta a], 其中\Delta a是单个采样周期内加速度最大变化值} σv的选择为[0.5Δa,Δa],其中Δa是单个采样周期内加速度最大变化值。

- update
以一阶系统为例,推导下面的关系。
第一种情况,假设传感器只能测量位置信息
Z k = H X + V k = [ 1 0 0 0 ] [ x x ˙ ] + [ v x 0 ] (4.25) \begin{aligned} Z_k & =HX+V_k \\ & = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \end{bmatrix} + \begin{bmatrix} v_x \\ 0 \end{bmatrix} \end{aligned} \tag{4.25} Zk=HX+Vk=[1000][xx˙]+[vx0](4.25)
先把K放在一边(K计算比较麻烦),计算尝试取计算P。
x − x ^ = x − ( x ‾ + K ( z − H x ‾ ) ) = x − ( x ‾ + K ( H x + V k − H x ‾ ) ) = ( I − K H ) ( x − x ‾ ) − K V k (4.26) \begin{aligned} x-\hat{x} &=x-(\overline{x}+K(z-H\overline{x})) \\ & = x-(\overline{x}+K(Hx+V_k-H\overline{x})) \\ & = (I-KH)(x-\overline{x})-KV_k \end{aligned} \tag{4.26} x−x^=x−(x+K(z−Hx))=x−(x+K(Hx+Vk−Hx))=(I−KH)(x−x)−KVk(4.26)
计算添加了测量数值后的方差,假设噪声是白噪声,即 E [ V k ] = 0 E[V_k]=0 E[Vk]=0
P = E [ ( x − x ^ ) ( x − x ^ ) ] = E [ ( ( I − K H ) ( x − x ‾ ) − K V k ) ( ( I − K H ) ( x − x ‾ ) − K V k ) T ] = ( I − K H ) ( x − x ‾ ) ( x − x ‾ ) T ( I − K H ) T + K V k V k T K T − 2 ( I − K H ) ( x − x ‾ ) E [ V k ] T K T = ( I − K H ) P ‾ ( I − K H ) T + K R K T (4.27) \begin{aligned} P &=E[(x-\hat{x})(x-\hat{x})] \\ &=E[((I-KH)(x-\overline{x})-KV_k) ((I-KH)(x-\overline{x})-KV_k)^T] \\ &=(I-KH)(x-\overline{x})(x-\overline{x})^T(I-KH)^T + KV_kV_k^TK^T-2(I-KH)(x-\overline{x})E[V_k]^TK^T \\ &= (I-KH)\overline{P}(I-KH)^T+KRK^T \end{aligned} \tag{4.27} P=E[(x−x^)(x−x^)]=E[((I−KH)(x−x)−KVk)((I−KH)(x−x)−KVk)T]=(I−KH)(x−x)(x−x)T(I−KH)T+KVkVkTKT−2(I−KH)(x−x)E[Vk]TKT=(I−KH)P(I−KH)T+KRKT(4.27)
这样就得到了P,接下来就是研究K是如何计算的。希望取一个非常合理的K,使得P的数值最小。
d P d K = 0 (4.28) \begin{aligned} \frac{dP}{dK} =0 \end{aligned} \tag{4.28} dKdP=0(4.28)
在因为P和K是矩阵,所以采用矩阵的trace计算倒数,在进一步计算之前,有两个公式至关重要(AB是方阵,C是对称矩阵)
d t r a c e ( A B ) d A = B T d t r a c e ( A C A T ) d A = 2 A C (4.29) \begin{aligned} \frac{d trace(AB)}{dA} & =B^T \\ \frac{d trace(ACA^T)}{dA} &=2AC \\ \end{aligned} \tag{4.29} dAdtrace(AB)dAdtrace(ACAT)=BT=2AC(4.29)
再结合(4.27和4.28)计算K
d t r a c e ( P ) d K = 2 ( K H − I ) P ‾ H T + 2 K R = 0 (4.30) \begin{aligned} \frac{dtrace(P)}{dK} =2(KH-I)\overline{P}H^T+2KR =0 \end{aligned} \tag{4.30} dKdtrace(P)=2(KH−I)PHT+2KR=0(4.30)
根据(4.30)可以计算K为
K = P ‾ H T ( H P ‾ H T + R ) − 1 K=\overline{P}H^T(H\overline{P}H^T+R)^{-1} K=PHT(HPHT+R)−1
关于观测方差R,是一个m*m矩阵(m是传感器的个数),例如有位置和速度两个传感器。
R = [ σ x 2 0 0 σ v 2 ] R= \begin{bmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_v^2 \end{bmatrix} R=[σx200σv2]
传感器的方差就是传感器噪声的功率谱。
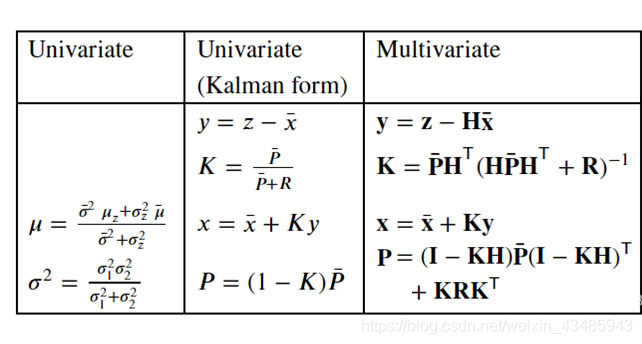
理论部分的回顾到此结束,下一章节开始进入线性卡尔曼滤波的应用。
References
[1] https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python
[2] https://www.youtube.com/watch?v=whSw42XddsU










 本文深入探讨了卡尔曼滤波的原理与应用,包括gh滤波、离散贝叶斯滤波器、单变量及多变量卡尔曼滤波,详细解析了预测与更新步骤,以及与互补滤波器的关系。
本文深入探讨了卡尔曼滤波的原理与应用,包括gh滤波、离散贝叶斯滤波器、单变量及多变量卡尔曼滤波,详细解析了预测与更新步骤,以及与互补滤波器的关系。
















 3044
3044

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








