MC采样（随机投点法）——附代码

1.MC采样(随机投点法)理论基础

在数学上，一般用蒙特卡罗方法去估计 一些不能求解的积分值。
                 ~~~~~~~~~~~~~~~~                  核心思想：面积占比。积分值在理论上可以表示为面积。
在统计学，蒙特卡罗方法一般用于求解给定概率密度函数下的采样点集合。
                 ~~~~~~~~~~~~~~~~                  主要方法：根据概率密度函数建立拒绝接受机制。

用蒙特卡罗方法计算定积分(随机投点法)
设0<=f(x)<=1,求f(x)在区间[0,1]上的积分值
$$J={\int }_0^{1}f(x)dx\text{\hspace{1em}(1)}$$
设二维随机变量（X,Y）服从正方形{0<=x<=1，0<=y<=1}上的均匀分布，则可知X服从[0,1]上的均匀分布，Y也服从[0,1]上的均匀分布，且X与Y独立。又记事件A={Y<=f(X)},则
$$P(A)=P(Y<=f(X))={\int }_{-\infty }^{+\infty }{\int }_0^{f(x)}dydx={\int }_{-\infty }^{+\infty }f(x)dx={\int }_0^{1}f(x)dx=J\text{\hspace{1em}(2)}$$
即定积分的值J就是事件A的概率p.由伯努利大数定律，我们可以用重复实验中A出现的频率作为p的估计值。
这种求定积分的方法也称随机投点法，即将（X,Y）看成是向正方形{0<=x<=1，0<=y<=1}内的随机投的点，用随机投的点落在区域{y<=f(x)}中的频率作为定积分的近似值。

2.具体步骤：

（1）先用计算机产生（0，1）上均匀分布的n对随机数(xi,yi),i=1,2,…n,这里n可以很大，建议取n=10000,n=100000.
（2）对n对数对(xi,yi),i=1,2,…n,记录满足如下不等式
$$yi<=f(xi)\text{\hspace{1em}(3)}$$
的次数，这就是事件A发生的频数Sn,由此可得事件A发生的频率$\frac{Sn}{n}$.可以近似估计J值。
满足式（3）不等式的xi样本点集合即为按照概率密度f(x)采样得到的样本点集合。

3. 概念理解

建立拒绝接受机制，若y<f(x)，则接受该样本点。

从概率论角度理解：采样点依概率分布发生,概率大的事件比较容易发生。

从几何角度理解：

拒绝接受机制会在x*y矩形中随机均匀撒点，但是只有在曲线f(x)下面的点会被接受成为样本点。
进一步，因为是均匀撒点，概率密度小的地方采样点数量少，密度大的地方采样点数量多。随即均匀采样保证了被采样的点集合的概率密度分布与f(x)吻合。
综上采样可行的保障机制：（均匀采样）and (y<f(x))
因为当{0<=x<=1，0<=y<=1}时，整个矩形面积为$1\times 1$，曲线面积为函数积分面积J，所以有效采样概率为$\frac{J}{1\times 1}=J$

概率密度函数

$f(x)=\frac{(x-0.4{)}^4}{{\int }_0^1(x-0.4{)}^{4}dx}$

采样区间[0,1]

import numpy as np
import matplotlib.pyplot as plt
import math
import random
import os 

#概率密度函数f（x）=(x-0.4)^4/f_0_1(x-0.4)^4dx
#积分区间[0,1]

#step1 生成随机数种子，确保实验可复现
seed=13
random.seed(seed)
np.random.seed(seed)
os.environ['PYTHONHASHSEED']=str(seed)

#step2 建立拒绝接受机制，若y<f(x)接受该样本点，
#理论：采样点依概率分布发生,概率大的事件比较容易发生。
#从几何角度考虑，下面的机制会在x*y矩形中随机均匀撒点，但是只有在曲线f(x)下面的点会被接受成为样本点
##进一步，因为是均匀撒点，保证曲线下面点发生的概率分布符合f(x),密度小的地方采样点的数量少，密度大的地方采样点数量多，
###保证了被采样的点集合的概率密度分布与f(x)吻合
###有效性保障机制：1均匀采样，2y<f(x)。
###有效采样概率为（1/maxf(x)）因为整个矩形面积为maxf(x)，曲线面积为函数积分面积为1，占比1/（1/maxf(x)）
def acceptreject(split_value):
    global t
    global power
    global sum_
    global max_fx
    x=random.uniform(0,1)
    y=random.uniform(0,max_fx)
    if y<=math.pow(x-0.4,4)/sum_:
        return x

#step3设置概率密度函数相关参数
t=0.4
power=4
sum_=(math.pow(1-0.4,5)-math.pow(0-0.4,5))/5
max_fx=math.pow(1-0.4,4)/sum_
x=np.linspace(0,1,100)
maxfx=[max_fx for i in x]
fx=[math.pow(xi-0.4,4)/sum_ for xi in x]

#step4 循环采样得到有效采样值集合（以列表形式表现）
samples=[acceptreject(t) for i in range(100000)]
samples=[i for i in samples if i is not None]#去除原列表无效采样值
print("迭代100000次，有效采样个数{}".format(len(samples)))
print("1/max_fx={:.4f}".format(1/max_fx))

#绘图
plt.plot(x,maxfx,'--',label='maxf(x)')
plt.plot(x,fx,label='f(x)',color='yellow')
plt.hist(samples,bins=50,density=True,label='samples',color='yellow')
plt.legend(loc='upper right',title='function')
plt.show()

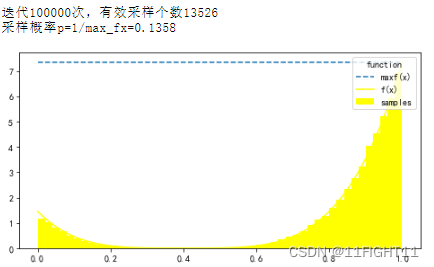
上述代码中，有效采样点集合存储在samples列表里。
上图中看出，有效采样点集合概率密度分布与f（x）一致，可以认为其是f（x）的成功采样点集合。

附加：
1.如何实现采取原概率密度函数$f(x)=\frac{(x-0.4{)}^4}{{\int }_0^1(x-0.4{)}^{4}dx}$在[0,0.4]或者[0.4,1]区间上的采样集合？（采取[0,1]区间采样集合——将集合中元素根据大小区分——分别得到[0,0.4]或者[0.4,1]区间上的采样集合。
2.如何采取$f(x)=\frac{(x-0.4{)}^4}{{\int }_0^{0.4}(x-0.4{)}^{4}dx}$在[0,0.4]区间上的采样集合？
或者如何采取$f(x)=\frac{(x-0.4{)}^4}{{\int }_{0.4}^1(x-0.4{)}^{4}dx}$在[0.4,1]区间上的采样集合？

后续会更新

参考文章：
1.马尔可夫链蒙特卡罗算法（MCMC）
2.markdown最简单的公式居中以及编号方法
3.markdown 数学公式 累加、连乘与乘号的代码