Swin Transformer源码——超详细图解

凯尔哥

已于 2024-12-16 10:42:02 修改

阅读量2.9k

点赞数 43

分类专栏：深度学习源码图解系列文章标签： transformer 深度学习人工智能

于 2024-02-23 14:20:50 首次发布

本文链接：https://blog.csdn.net/weixin_43507865/article/details/136254557

版权

深度学习源码图解系列专栏收录该内容

5 篇文章

订阅专栏

论文地址：https://arxiv.org/pdf/2103.14030.pdf

模型原理：Swin-Transformer网络结构详解_swin transformer-CSDN博客

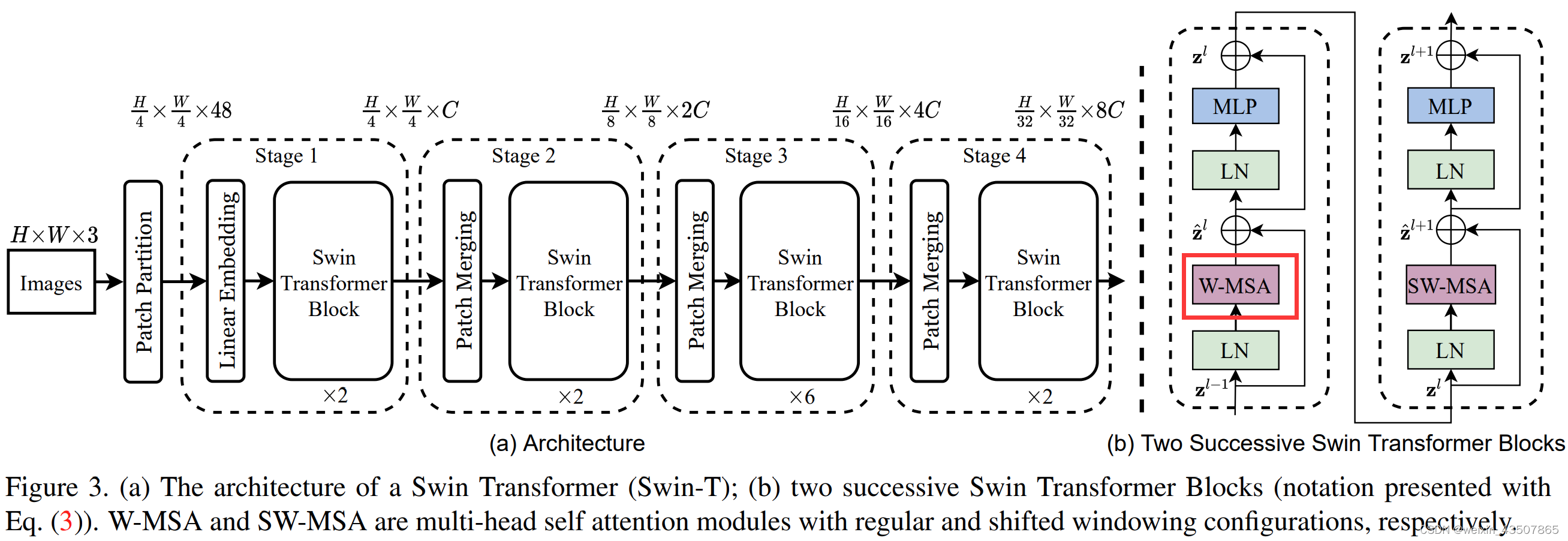
模型代码：https://github.com/WZMIAOMIAO/deep-learning-for-image-processing/tree/master/pytorch_classification/swin_transformer

1. 整体流程图

2. PatchEmbedding

输入：预处理之后的原始图像（这里为了演示方便，将每张图像缩放成 16*16*3，每个批次为 2，因此输入的维度是(2, 3, 16, 16)）

处理：nn.Conv2d

输出：(2, 16, 8)

在源码中，实际上就是一个卷积操作。 x = self.proj(x)，self.proj = nn.Conv2d(in_c, embed_dim, kernel_size=patch_size, stride=patch_size)

输入 x 的 shape 为(B, C, H, W)，输出 x 的 shape 为(B, C, H, W)。假设输入 x 的 shape 为(2,3,16,16)，那么输出 x 的 shape 为(2,8,4,4)。

在卷积操作之后，还需要对形状做一次变形。x = x.flatten(2).transpose(1, 2)，假设输入 x 的 shape 为(2,8,4,4)，那么输出 x 的 shape 为(2,16,8)。如下图所示：

3. SwinTransformerBlock

3.1. W-MSA 部分中的第一个 LN 层

输入：PatchEmbedding 的输出，即(2, 16, 8)

处理：nn.LayerNorm

输出：(2, 4, 4, 8)

x = self.norm1(x)		# 层标准化
x = x.view(B, H, W, C)	# 改变tensor形状，(2, 4, 4, 8)

x = self.norm1(x)的结果如下：

x = x.view(B, H, W, C)的结果如下：

3.2. W-MSA

先对 x 进行重构

# 把feature map给pad到window size的整数倍
pad_l = pad_t = 0
pad_r = (self.window_size - W % self.window_size) % self.window_size
pad_b = (self.window_size - H % self.window_size) % self.window_size
x = F.pad(x, (0, 0, pad_l, pad_r, pad_t, pad_b))	# (2, 6, 6, 8)

x = F.pad(x, (0, 0, pad_l, pad_r, pad_t, pad_b))的结果如下：

3.2.1. WindowPartition

将feature map按照window_size划分成一个个没有重叠的window

def window_partition(x, window_size: int):
    """
    将feature map按照window_size划分成一个个没有重叠的window
    Args:
        x: (B, H, W, C)
        window_size (int): window size(M)

    Returns:
        windows: (num_windows*B, window_size, window_size, C)
    """
    B, H, W, C = x.shape
    x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)  # (2,2,3,2,3,8)
    # permute: [B, H//Mh, Mh, W//Mw, Mw, C] -> [B, H//Mh, W//Mh, Mw, Mw, C]
    # view: [B, H//Mh, W//Mw, Mh, Mw, C] -> [B*num_windows, Mh, Mw, C]
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)  # (8,3,3,8)
    return windows

x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)的结果如下：

windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)的结果如下(8,3,3,8)：

x_windows = x_windows.view(-1, self.window_size * self.window_size, C)的结果如下(8,9,8)：

对于一张图片的特征图，划分出了 4 个 window，如下图所示：

3.2.2. q、k、v

qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)

w_q,w_k,w_v 的 shape 为(8, 24)

qkv(): -> [batch_size*num_windows, Mh*Mw, 3 * total_embed_dim], [2*4, 3*3, 3*8]
reshape: -> [batch_size*num_windows, Mh*Mw, 3, num_heads, embed_dim_per_head], [2*4, 3*3, 3, 2, 4]
permute: -> [3, batch_size*num_windows, num_heads, Mh*Mw, embed_dim_per_head], [3, 2*4, 2, 3*3, 4]

q, k, v = qkv.unbind(0)，将 q、k、v 拆分开

q: ->[batch_size*num_windows, num_heads, Mh*Mw, embed_dim_per_head], [2*4, 2, 3*3, 4]
k: ->[batch_size*num_windows, num_heads, Mh*Mw, embed_dim_per_head], [2*4, 2, 3*3, 4]
v: ->[batch_size*num_windows, num_heads, Mh*Mw, embed_dim_per_head], [2*4, 2, 3*3, 4]

解释下上面 q（k 和 v 是一样的）的 shape，一个 batch 中的每一张图片中的每一个 window 的每个 head 都有自己的 q、k、v 值。

3.2.3. 计算 attention

attention 的计算公式如下：

$\operatorname{Attention}(\mathrm{Q}, \mathrm{K}, \mathrm{V})=\operatorname{SoftMax}\left(\frac{\mathrm{QK}^{\mathrm{T}}}{\sqrt{\mathrm{d}}}\right) \mathrm{V}$

q = q * self.scale，即 Q / √d

attn = (q @ k.transpose(-2, -1)), @: multiply, q @ k.transpose(-2, -1)) 即 $\mathrm{QK}^{\mathrm{T}}$ 。attn 的 shape 为(8, 2, 9, 9)

3.2.3.1. Relative Position Bias

swintransformer 使用了如下公式来计算最终的 attention 值，

$\operatorname{Attention}(\mathrm{Q}, \mathrm{K}, \mathrm{V})=\operatorname{SoftMax}\left(\frac{\mathrm{QK}^{\mathrm{T}}}{\sqrt{\mathrm{d}}} + B\right) \mathrm{V}$

上面公式中的 B 就是Relative Position Bias

3.2.3.2. relative position bias table

有一个relative position bias table，里面保存了每个相对位置的偏置参数，其大小为(2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads)

self.relative_position_bias_table = nn.Parameter(torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads))，定义relative_position_bias_table 参数，初始值都为 0，shape 为(25, 2)：

coords_h = torch.arange(self.window_size[0])
coords_w = torch.arange(self.window_size[1])
coords = torch.stack(torch.meshgrid([coords_h, coords_w], indexing="ij"))  # [2, Mh, Mw]
coords_flatten = torch.flatten(coords, 1)
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # [2, Mh*Mw, Mh*Mw]
relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # [Mh*Mw, Mh*Mw, 2]

relative_coords 的结果如下：

relative_coords[:, :, 0] += self.window_size[0] - 1 , 每个位置的横坐标+2，结果如下：

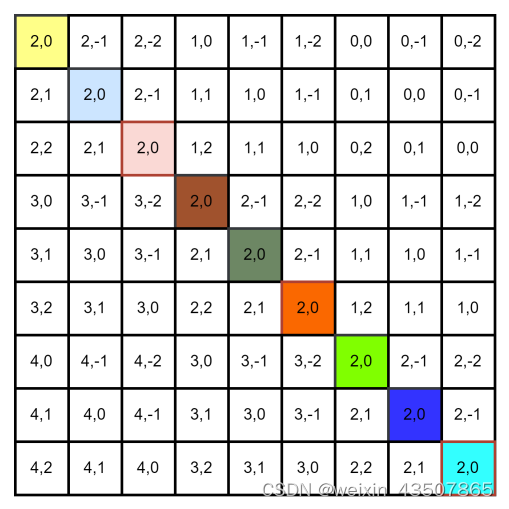
relative_coords[:, :, 1] += self.window_size[1] - 1 ，每个位置的纵坐标+2，结果如下：

relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1 ，每个位置的横坐标 * 5，结果如下：

relative_position_index = relative_coords.sum(-1)的结果如下：

根据relative_position_index 从relative_position_bias_table 中查找偏置值

relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1)，shape 为(9, 9, 2)

relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()，shape 为(2, 9, 9), 表示

attn = attn + relative_position_bias.unsqueeze(0), (8, 2, 9, 9) + (2, 9, 9) = (8, 2, 9, 9)

以一个 window 举例，如下图所示：

attn = self.softmax(attn)，即公式 $\operatorname{Attention}(\mathrm{Q}, \mathrm{K}, \mathrm{V})=\operatorname{SoftMax}\left(\frac{\mathrm{QK}^{\mathrm{T}}}{\sqrt{\mathrm{d}}} + B\right) \mathrm{V}$

中的 softmax 函数。

x = (attn @ v).transpose(1, 2).reshape(B_, N, C)，其中attn @ v 即为公式 $\operatorname{Attention}(\mathrm{Q}, \mathrm{K}, \mathrm{V})=\operatorname{SoftMax}\left(\frac{\mathrm{QK}^{\mathrm{T}}}{\sqrt{\mathrm{d}}} + B\right) \mathrm{V}$ 中的最后一个部分。reshape 之后的 shape 为(8, 9, 8)。

attn_windows = self.attn(x_windows, mask=attn_mask)，到这里 attn 就计算完了。

attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C)，shape 为(8, 3, 3, 8)

shifted_x = window_reverse(attn_windows, self.window_size, Hp, Wp)，将一个个 window 还原成 feature map。shape 为(2, 6, 6, 8)，其中 2 表示 batch_size；8 表示特征维度，又还原成下图的样子了（针对一张图片）：

从上图看出，还有之前 pad 的数据，因此需要把它移除掉。x = x[:, :H, :W, :].contiguous()，shape 为(2, 4, 4, 8)

再对维度进行整合，x = x.view(B, H * W, C)，shape 为(2, 16, 8)

3.3. W-MSA 中的第二个 LN 层 + MLP

x = shortcut + self.drop_path(x)

x = x + self.drop_path(self.mlp(self.norm2(x)))

3.4. SW-MSA 中第一个 LN 层

进入到 SW-MSA 部分，先还是有一个 LN 层，代码和之前的代码都是一样的。

3.5. SW-MSA

3.5.1. 特征图滑动

shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))，

x 如左图所示，shifted_x 如右图所示：

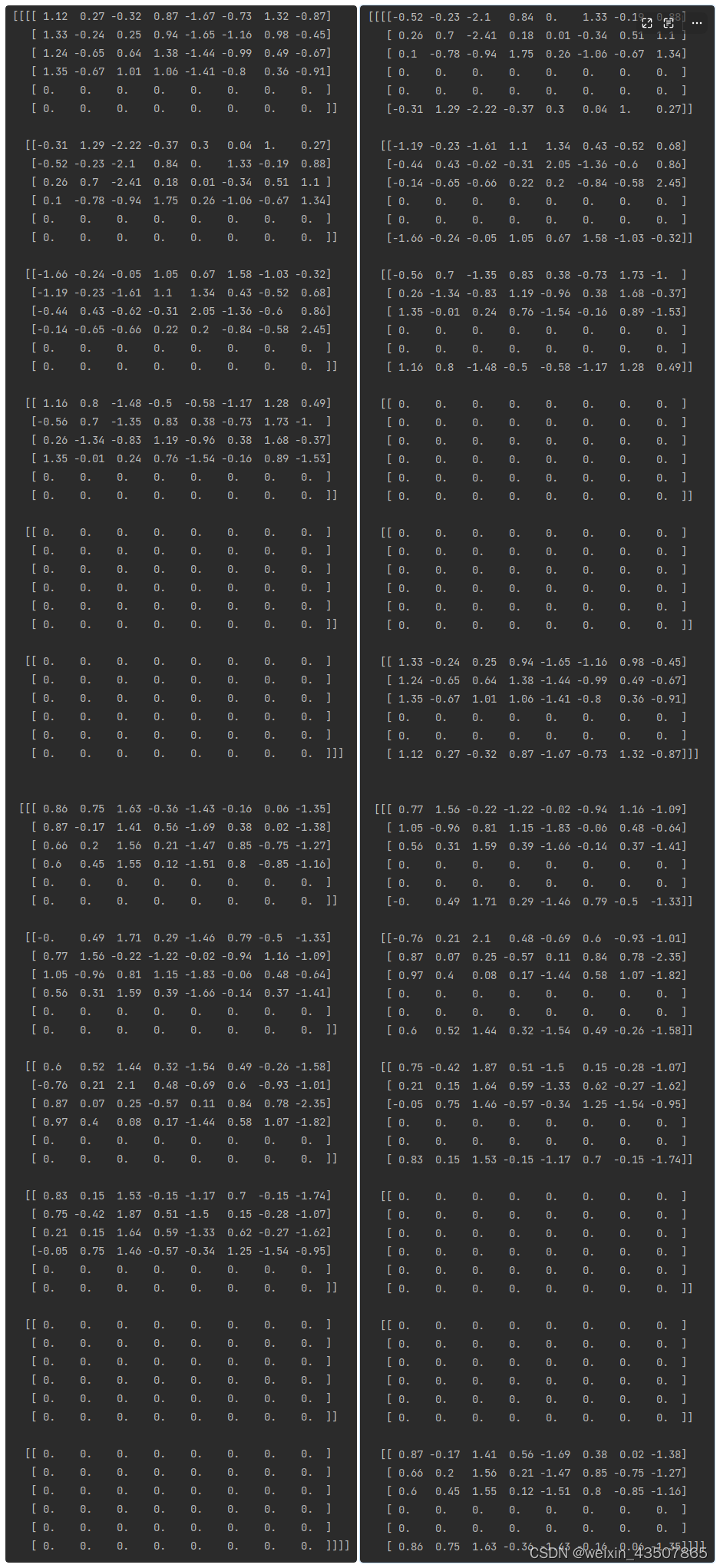
用特征图表示如下：

3.5.2. WindowPartition

同 W-MSA 部分的代码一样，这里就不再重复了。得到 4 个 window 的特征图，如下图所示：

3.5.3. attention mask

先说一下为什么需要 attention mask，在 SW-MSA 中，需要对特征图进行滑动，如下图所示：

说明：在我的代码中，生成的特征图是 4*4 的，而 window_size 为 3，因此需要对特征图进行扩充，以适应窗口大小。上图用字母标注的区域都是扩充的部分；

对于滑动之后的特征图，如果还是像 W-MSA 中直接对每个 3*3 的窗口计算 attention 值的话，就会有问题。

滑动后新生成的 4 的 window，对于第一个 window，可以直接计算 attention 值，这是没有问题的。但是对于第 2、3、4 个窗口，就不能直接计算 attention 值了，信息会乱窜。

上图所示，需要单独对每个子区域计算 attention 值，相当于总共要计算 9 个区域的 attention 值。但是在 W-MSA 中，只计算了 4 个区域的 attention 值，为了保证计算量一样，源码中引入了 attention mask。其作用是还是计算 4 个区域的 attention 值，但是对于第 2、3、4 个窗口，每个子区域单独计算 attention 值。

attention mask 的生成过程如下：

img_mask(1, 6, 6, 1)

Hp = int(np.ceil(H / self.window_size)) * self.window_size	# window_size=3  Hp=6
Wp = int(np.ceil(W / self.window_size)) * self.window_size	# Wp = 6
# 拥有和feature map一样的通道排列顺序，方便后续window_partition
img_mask = torch.zeros((1, Hp, Wp, 1), device=x.device)
h_slices = (slice(0, -self.window_size),
            slice(-self.window_size, -self.shift_size),
            slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
            slice(-self.window_size, -self.shift_size),
            slice(-self.shift_size, None))
cnt = 0
for h in h_slices:
    for w in w_slices:
        img_mask[:, h, w, :] = cnt
        cnt += 1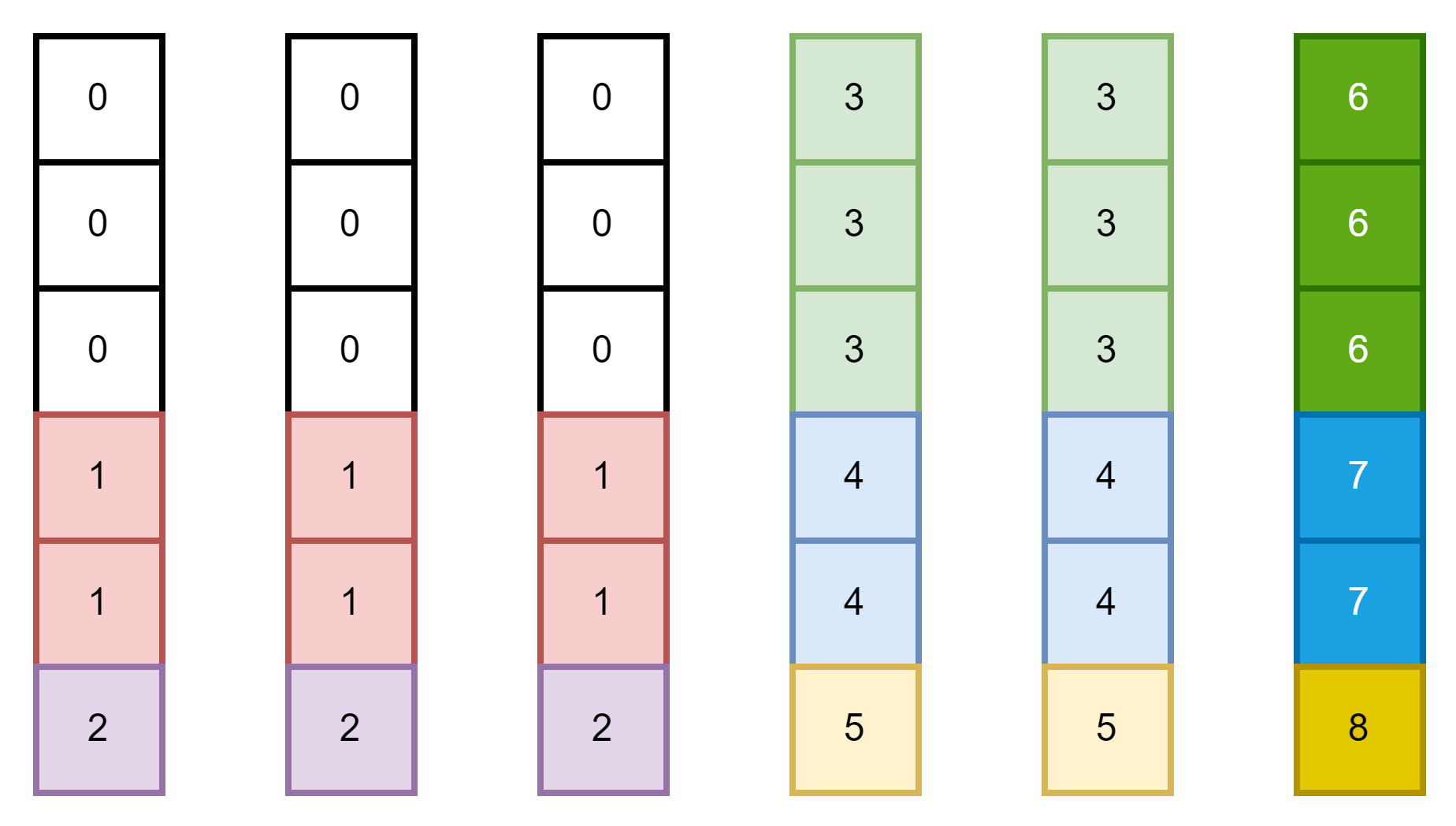

mask_window(4, 9)

mask_windows = window_partition(img_mask, self.window_size)  # [nW, Mh, Mw, 1]
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)  # [nW, Mh*Mw]

attn_mask(4, 9, 9)

attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)

attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))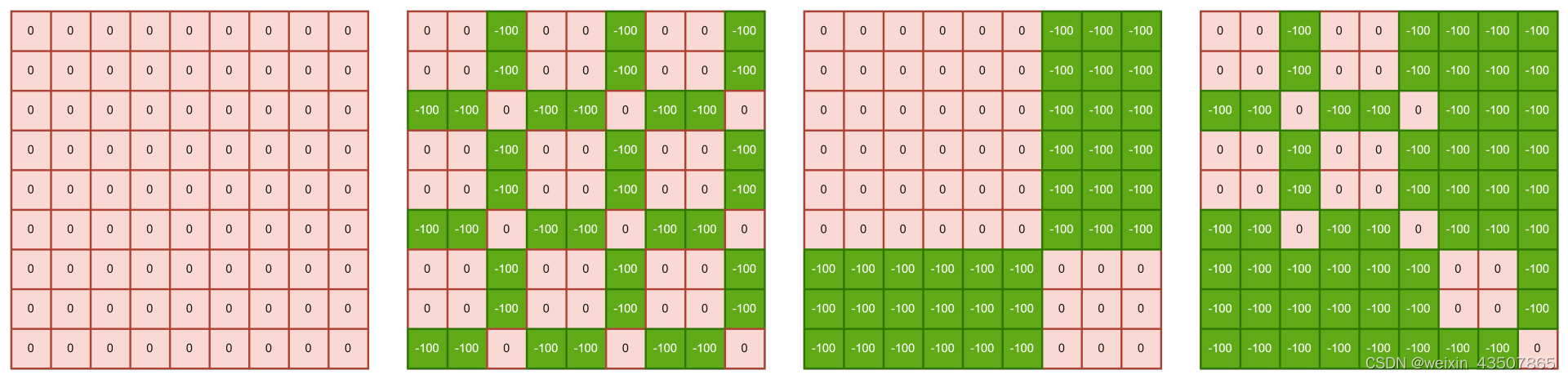

3.5.4. 计算 attention

每个 window 的 q 和 k 矩阵进行计算，得到 9*9 的 attention 矩阵

attn = (q @ k.transpose(-2, -1))

然后加上相对位置的偏移值

relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
    self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1)
relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()  # [nH, Mh*Mw, Mh*Mw]
attn = attn + relative_position_bias.unsqueeze(0)

然后加上 attention mask

if mask is not None:
    # mask: [nW, Mh*Mw, Mh*Mw]
    nW = mask.shape[0]  # num_windows
    # attn.view: [batch_size, num_windows, num_heads, Mh*Mw, Mh*Mw],[2, 4, 2, 9, 9]
    # mask.unsqueeze: [1, nW, 1, Mh*Mw, Mh*Mw], [1, 4, 1, 9, 9]
    attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
    attn = attn.view(-1, self.num_heads, N, N)
    attn = self.softmax(attn)

如下图所示：

即，每个窗口的子区域单独计算 attention 值。

举个例子：上图中的第二个 window，b1 的 q 只需要同 b1、b2、c1、c2、d1、d2 的 k 计算 attention 值，即 q_b1*k_b1, q_b1*k_b2,q_b1*k_4,q_b1*k_c1,q_b1*k_c2,q_b1*k_8,q_b1*k_d1,q_b1*k_d2,q_b1*k_12,红色的部分就是上图中第一行的三个-100 值的位置，-100 的位置在经过 softmax 之后就会变成 0，相当于没有计算当前位置的 attention 值。

3.6. SW-MSA 中的第二个 LN 层 + MLP

x = shortcut + self.drop_path(x)
x = x + self.drop_path(self.mlp(self.norm2(x)))

4. PatchMerging

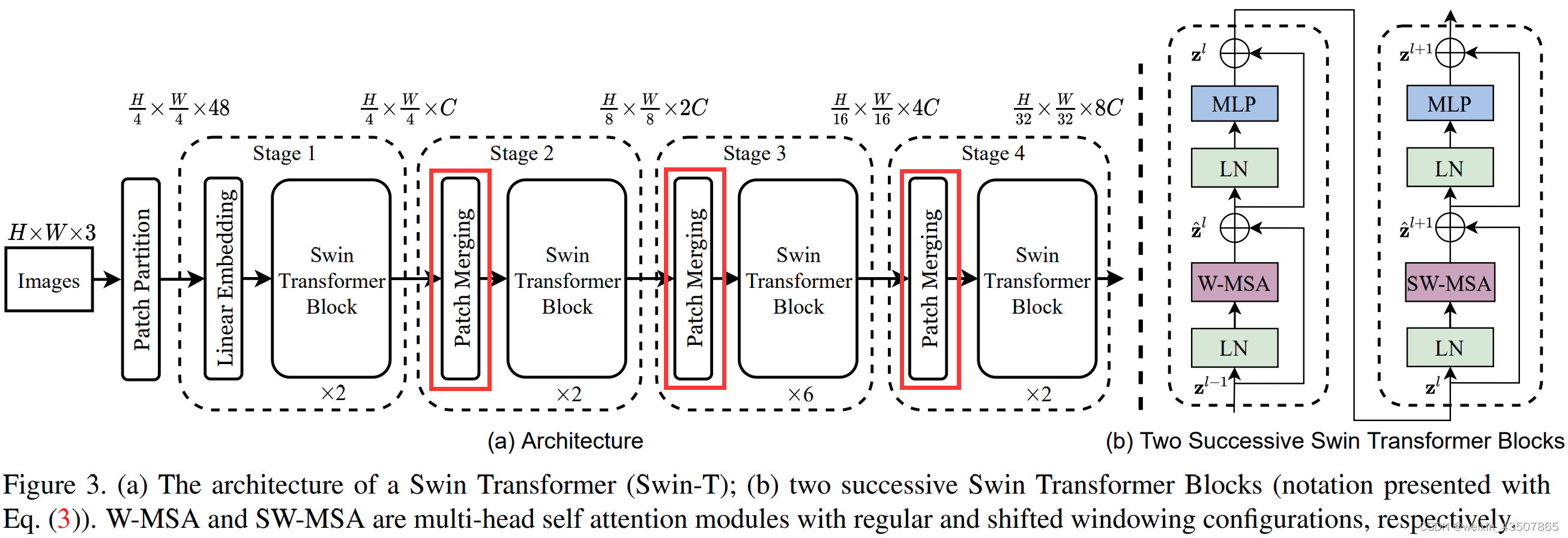
def forward(self, x, H, W):
    """
    x: B, H*W, C
    """
    B, L, C = x.shape
    assert L == H * W, "input feature has wrong size"

    x = x.view(B, H, W, C)

    # padding
    # 如果输入feature map的H，W不是2的整数倍，需要进行padding
    pad_input = (H % 2 == 1) or (W % 2 == 1)
    if pad_input:
        # to pad the last 3 dimensions, starting from the last dimension and moving forward.
        # (C_front, C_back, W_left, W_right, H_top, H_bottom)
        # 注意这里的Tensor通道是[B, H, W, C]，所以会和官方文档有些不同
        x = F.pad(x, (0, 0, 0, W % 2, 0, H % 2))

    x0 = x[:, 0::2, 0::2, :]  # [B, H/2, W/2, C]
    x1 = x[:, 1::2, 0::2, :]  # [B, H/2, W/2, C]
    x2 = x[:, 0::2, 1::2, :]  # [B, H/2, W/2, C]
    x3 = x[:, 1::2, 1::2, :]  # [B, H/2, W/2, C]
    x = torch.cat([x0, x1, x2, x3], -1)  # [B, H/2, W/2, 4*C]
    x = x.view(B, -1, 4 * C)  # [B, H/2*W/2, 4*C]

    x = self.norm(x)
    x = self.reduction(x)  # [B, H/2*W/2, 2*C]

    return x