深度学习复习笔记

最新推荐文章于 2025-10-23 21:18:02 发布

原创

最新推荐文章于 2025-10-23 21:18:02 发布 · 2.3k 阅读

35 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习

这篇深度学习复习笔记涵盖了神经元构造、前馈神经网络的激活函数（如Sigmoid、ReLU及其改进），卷积神经网络的卷积概念与参数理解，循环神经网络的长程依赖问题和LSTM，以及网络优化方法。笔记讨论了梯度消失问题、学习率调整和参数初始化，同时介绍了PCA在无监督学习中的应用。

深度学习（邱锡鹏）HDU复习笔记 A

第1章绪论

神经元的构造

典型的神经元结构大致可分为细胞体和细胞突起．
（1）细胞体（Soma）中的神经细胞膜上有各种受体和离子通道，胞膜的受体可与相应的化学物质神经递质结合，引起离子通透性及膜内外电位差发生改变，产生相应的生理活动：兴奋或抑制．
（2）细胞突起是由细胞体延伸出来的细长部分，又可分为树突和轴突．
a ) 树突（Dendrite）可以接收刺激并将兴奋传入细胞体．每个神经元可以有一或多个树突．
b ) 轴突（Axon）可以把自身的兴奋状态从胞体传送到另一个神经元或其他组织．每个神经元只有一个轴突．
神经元之间通过突触进行互联来传递信息，有兴奋和抑制两种状态

神经网络的发展历史

在这里插入图片描述

第2章前馈神经网络

激活函数相关知识Sigmoid（Logistic、Tanh）RELU优缺点和不足，需要改进的地方

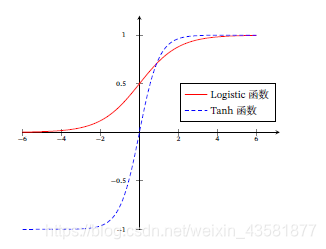
Sigmoid型函数，常用的Sigmoid型函数有Logistic 函数和Tanh 函数．
Logistic 函数
优点：平滑、易于求导。

缺点：

激活函数计算量大（在正向传播和反向传播中都包含幂运算和除法）；
反向传播求误差梯度时，求导涉及除法；
Logistic导数取值范围是[0, 0.25]，由于神经网络反向传播时的“链式反应”，很容易就会出现梯度消失的情况。
Logistic的输出不是0均值（即zero-centered）；这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入，随着网络的加深，会改变数据的原始分布。
$\sigma(x) = \frac{1}{1+exp(-x)}$
Tanh 函数
tanh 是双曲正切函数，tanh 函数和 Logistic 函数的曲线是比较相近。首先，在输入很大或是很时，输出都几乎平滑，梯度很小，不利于权重更新；不同的是输出区间，tanh的输出区间是在 (-1,1) z之间，而且整个函数是以0为中心的，这个特点比 Logistic 的好。
$\frac{exp(x)-exp(-x)}{exp(x)+exp(-x)}$

在这里插入图片描述
ReLU
$\begin{cases} x, \quad x \geq 0 \\ 0, \quad x < 0 \end{cases} \\ =max(0,x)$
ReLU作为激活函数的特点：
优点：在优化方面，相比于Sigmoid 型函数的两端饱和，ReLU 函数为左饱和函数，且在𝑥 > 0 时导数为1，在一定程度上缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度．

缺点：ReLU 函数的输出是非零中心化的，给后一层的神经网络引入偏置偏移，会影响梯度下降的效率．此外，ReLU 神经元在训练时比较容易“死亡”．在训练时，如果参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU 神经元在所有的训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远不能被激活．这种现象称为死亡ReLU问题，并且也有可能会发生在其他隐藏层
改进：

Leaky ReLU
$\begin{cases} x, \quad if & x > 0 \\ \gamma x, \quad if & x \leq 0 \end{cases}\\ =max(0,x)+\gamma min(0,x)\\ 当\gamma <1 时\\ LeakyReLU(x) = max(a,\gamma x)$
PReLU
$pReLU_i(x) = \begin{cases} x, \quad if & x > 0 \\ \gamma_ix, \quad if & x \leq 0 \end{cases}\\ =max(0,x)+\gamma min(0,x)$
ELU
$\begin{cases} x, \quad if & x > 0 \\ \gamma(exp(x)-1), \quad if & x \leq 0 \end{cases}\\ =max(0,x)+min(0,\gamma(exp(x)-1)$