卡尔曼滤波状态估计

 

clear all;
close all;
clc;
%% 上面是调用卡尔曼滤波
% 定义状态维数和初始条件
n = 3;                               % 状态维数
q = 0.2;                             % 过程噪声标准差
r = 0.15;                             % 测量噪声标准差
Q = q * eye(n);                    % 过程噪声协方差矩阵
R = r^2;                             % 测量噪声协方差矩阵
fstate = @(x)[x(2); x(3); 0.5*x(1)*(x(2) + x(3))];  % 状态转移方程
hmeas = @(x)x(1);                                   % 测量方程

% 初始化状态和协方差矩阵
s = [0; 0; 1];                       % 真实初始状态
x = s + q * randn(3,1);              % 加入噪声的初始状态估计
P = eye(n);                          % 初始状态协方差矩阵

% 模拟参数
N = 200;                              % 动态步数
xV = zeros(n, N);                    % 保存状态估计值
sV = zeros(n, N);                    % 保存真实状态值
zV = zeros(1, N);                    % 保存测量值

% 开始模拟
for k = 1:N
    z = hmeas(s) + r * randn;        % 模拟测量值
    sV(:, k) = s;                    % 存储真实状态值
    zV(k) = z;                       % 存储测量值

    [x, P] = ukf(fstate, x, P, hmeas, z, Q, R); % 调用UKF
    xV(:, k) = x;                    % 存储状态估计值

    s = fstate(s) + q * randn(3, 1); % 更新真实状态
end

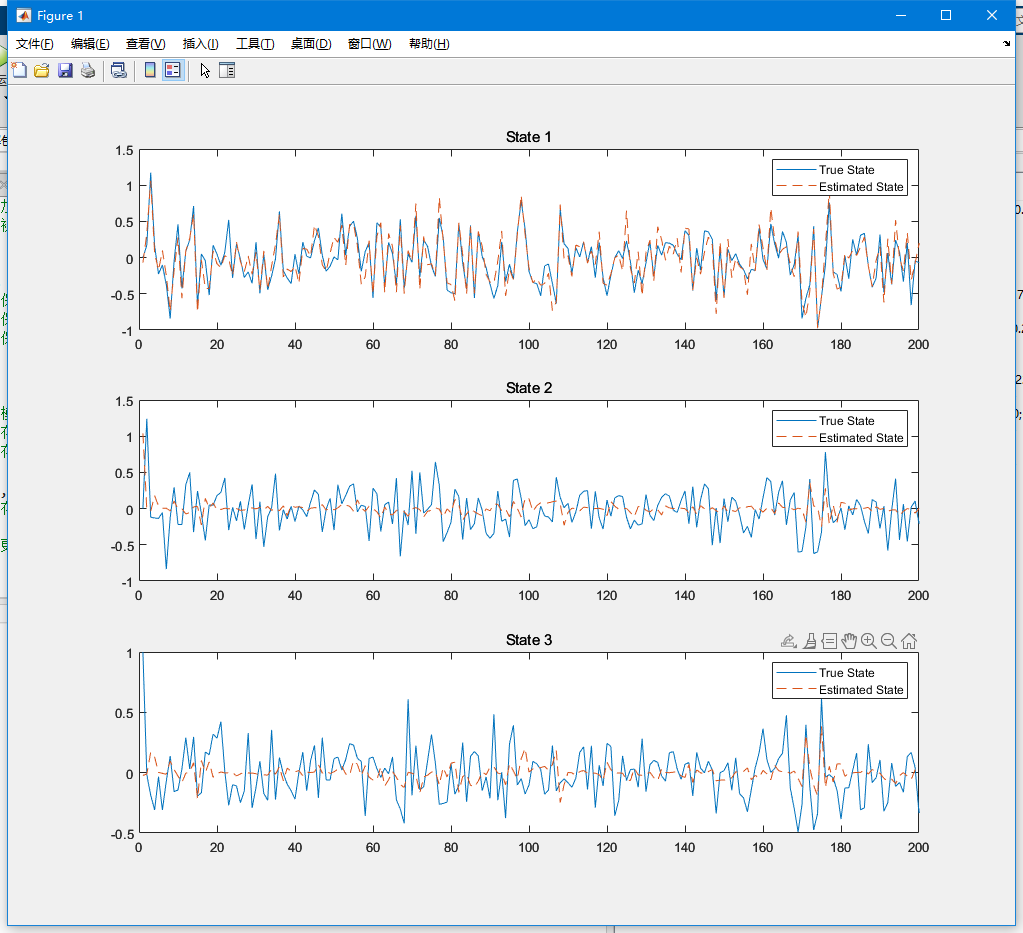
% 绘制结果
for k = 1:3
    subplot(3, 1, k)
    plot(1:N, sV(k, :), '-', 1:N, xV(k, :), '--')
    title(['State ', num2str(k)])
    legend('True State', 'Estimated State')
end



 function X=sigmas(x,P,c)
    %Sigma points around reference point
    %Inputs:
    %       x: reference point
    %       P: covariance
    %       c: coefficient
    %Output:
    %       X: Sigma points
    
        A = c*chol(P)';
        Y = x(:,ones(1,numel(x)));
        X = [x Y+A Y-A]; 
    end
  function [y,Y,P,Y1]=ut(f,X,Wm,Wc,n,R)
    %Unscented Transformation
    %Input:
    %        f: nonlinear map
    %        X: sigma points
    %       Wm: weights for mean
    %       Wc: weights for covraiance
    %        n: numer of outputs of f
    %        R: additive covariance
    %Output:
    %        y: transformed mean
    %        Y: transformed smapling points
    %        P: transformed covariance
    %       Y1: transformed deviations
    
        L=size(X,2);
        y=zeros(n,1);
        Y=zeros(n,L);
        for k=1:L                   
            Y(:,k)=f(X(:,k));       
            y=y+Wm(k)*Y(:,k);       
        end
        Y1=Y-y(:,ones(1,L));
        P=Y1*diag(Wc)*Y1'+R;          
    end


function [x,P]=ukf(fstate,x,P,hmeas,z,Q,R)
% UKF   Unscented Kalman Filter for nonlinear dynamic systems
% [x, P] = ukf(f,x,P,h,z,Q,R) returns state estimate, x and state covariance, P 
% for nonlinear dynamic system (for simplicity, noises are assumed as additive):
%           x_k+1 = f(x_k) + w_k
%           z_k   = h(x_k) + v_k
% where w ~ N(0,Q) meaning w is gaussian noise with covariance Q
%       v ~ N(0,R) meaning v is gaussian noise with covariance R
% Inputs:   f: function handle for f(x)
%           x: "a priori" state estimate
%           P: "a priori" estimated state covariance
%           h: fanction handle for h(x)
%           z: current measurement
%           Q: process noise covariance 
%           R: measurement noise covariance
% Output:   x: "a posteriori" state estimate
%           P: "a posteriori" state covariance
%
% Example:
%{
n=3;      %number of state
q=0.1;    %std of process 
r=0.1;    %std of measurement
Q=q^2*eye(n); % covariance of process
R=r^2;        % covariance of measurement  
f=@(x)[x(2);x(3);0.05*x(1)*(x(2)+x(3))];  % nonlinear state equations
h=@(x)x(1);                               % measurement equation
s=[0;0;1];                                % initial state
x=s+q*randn(3,1); %initial state          % initial state with noise
P = eye(n);                               % initial state covraiance
N=20;                                     % total dynamic steps
xV = zeros(n,N);          %estmate        % allocate memory
sV = zeros(n,N);          %actual
zV = zeros(1,N);
for k=1:N
  z = h(s) + r*randn;                     % measurments
  sV(:,k)= s;                             % save actual state
  zV(k)  = z;                             % save measurment
  [x, P] = ukf(f,x,P,h,z,Q,R);            % ekf 
  xV(:,k) = x;                            % save estimate
  s = f(s) + q*randn(3,1);                % update process 
end
for k=1:3                                 % plot results
  subplot(3,1,k)
  plot(1:N, sV(k,:), '-', 1:N, xV(k,:), '--')
end
%}
% Reference: Julier, SJ. and Uhlmann, J.K., Unscented Filtering and
% Nonlinear Estimation, Proceedings of the IEEE, Vol. 92, No. 3,
% pp.401-422, 2004. 
%
% By Yi Cao at Cranfield University, 04/01/2008
%
    L=numel(x);                                 %numer of states
    m=numel(z);                                 %numer of measurements
    alpha=1e-3;                                 %default, tunable
    ki=0;                                       %default, tunable
    beta=2;                                     %default, tunable
    lambda=alpha^2*(L+ki)-L;                    %scaling factor
    c=L+lambda;                                 %scaling factor
    Wm=[lambda/c 0.5/c+zeros(1,2*L)];           %weights for means
    Wc=Wm;
    Wc(1)=Wc(1)+(1-alpha^2+beta);               %weights for covariance
    c=sqrt(c);
    X=sigmas(x,P,c);                            %sigma points around x
    [x1,X1,P1,X2]=ut(fstate,X,Wm,Wc,L,Q);          %unscented transformation of process
    % X1=sigmas(x1,P1,c);                         %sigma points around x1
    % X2=X1-x1(:,ones(1,size(X1,2)));             %deviation of X1
    [z1,Z1,P2,Z2]=ut(hmeas,X1,Wm,Wc,m,R);       %unscented transformation of measurments
    P12=X2*diag(Wc)*Z2';                        %transformed cross-covariance
    K=P12*inv(P2);
    x=x1+K*(z-z1);                              %state update
    P=P1-K*P12';                                %covariance update
end
  

`sigmas` 函数：

sigmas函数用来生成一系列特殊的点，叫做σ点，它们围绕着我们估算的当前位置（也就是状态的均值），通过这些点可以反映出我们对当前位置的不确定性有多大。

这个函数的目的是计算σ点（Sigma Points），这是一组围绕状态均值`x`分布的点，能够捕捉状态的均值和协方差特性。在无迹卡尔曼滤波器（UKF）中，σ点是非常关键的，因为它们通过过程和测量模型的非线性变换来传播状态的分布。

- `x`：状态向量的均值，围绕它来生成σ点。

- `P`：与状态向量`x`相关的协方差矩阵。

- `c`：生成σ点时使用的缩放系数。

`A = c*chol(P)'`：这行代码计算了缩放协方差矩阵的Cholesky分解。这个分解用于以一种与状态不确定性一致的方式扩展σ点。

`Y = x(:,ones(1,numel(x)))`：这创建了一个矩阵，其中每一列都是状态向量`x`的副本。

`X = [x Y+A Y-A]`：这行代码按如下方式构造σ点集——状态`x`，然后是`x`加上矩阵`A`中的每一列（正偏差），最后是`x`减去矩阵`A`中的每一列（负偏差）。这些点旨在捕捉原始状态分布的均值和协方差。

 `ut` (无迹变换) 函数：

ut函数的作用是把这些σ点通过一个复杂的函数（可能会改变它们的形状和间距）转换到另一种形式，然后计算转换后的点的新均值和新不确定性。

这个函数应用无迹变换过程于σ点上。这是UKF过程中的关键步骤，它包括将σ点通过非线性函数传播，以估计新的均值和协方差。 - `f`：σ点通过的非线性状态或测量函数。 - `X`：σ点的矩阵。 - `Wm`：用于从变换后的σ点计算均值的权重。 - `Wc`：用于从变换后的σ点计算协方差的权重。 - `n`：函数`f`的输出数量（观测/测量的维度）。 - `R`：附加的测量噪声协方差。 该函数对每个σ点`X(:,k)`进行迭代，使用`f`对其进行变换，并计算加权均值`y`和样本点`Y`。然后，它计算变换点的协方差`P`（包括测量噪声`R`）。

`ukf` (无迹卡尔曼滤波) 函数：

ukf函数是无迹卡尔曼滤波的核心，它重复使用sigmas和ut来不断更新我们对系统状态的估计，并使用最新的测量数据来校正这个估计，使我们对系统的了解越来越精确。

这是UKF算法本身，使用`sigmas`函数确定围绕当前状态估计`x`的σ点，然后通过`ut`（无迹变换）将这些σ点通过过程模型和测量模型进行变换。随后，根据当前的测量`z`更新状态估计`x`和协方差`P`。

- `fstate`：代表系统动态的函数句柄。

- `x`：先验状态估计（测量更新之前）。

- `P`：先验状态协方差估计。

- `hmeas`：代表测量模型的函数句柄。

- `z`：当前的测量向量。

- `Q`：过程噪声协方差矩阵。

- `R`：测量噪声协方差矩阵。 函数最后的步骤是计算卡尔曼增益`K`，然后使用来自测量`z`的新信息更新`x`和`P`。这个过程有效地结合了过程模型的预测和实际的测量，以形成一个改进的状态估计和相应的不确定性。 这些是复杂的统计过程，而UKF本质上提供了一种在不线性化过程或测量模型的情况下处理非线性状态变换的方法。