《视觉SLAM十四讲 第二版》笔记及课后习题（第五讲）

读书笔记：相机与图像

相机模型

相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程能够用一个几何模型进行描述。这个模型有很多种，其中最简单的称为针孔模型。针孔模型是很常用，而且有效的模型，它描述了一束光线通过针孔之后，在针孔背面投影成像的关系。在本书中我们用一个简单的针孔相机模型来对这种映射关系进行建模。同时，由于相机镜头上的透镜的存在，会使得光线投影到成像平面的过程中会产生畸变。因此，我们使用针孔和畸变两个模型来描述整个投影过程。

针孔相机模型

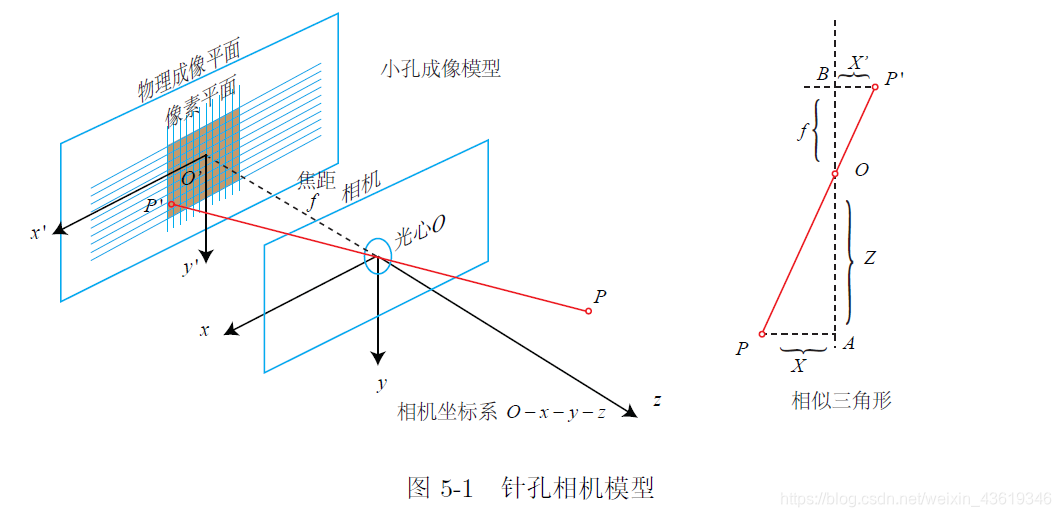
该式中，我们把中间的量组成的矩阵称为相机的内参数矩阵（Camera Intrinsics）K.
同一直线上的投影点仍是同一个
投影顺序：世界——相机——归一化平面——像素:(激光数据的观测模型更加简单)

畸变：



最后，我们小结一下单目相机的成像过程：

双目相机

针孔相机模型描述了单个相机的成像模型。然而，仅根据一个像素，我们是无法确定这个空间点的具体位置的。这是因为，从相机光心到归一化平面连线上的所有点，都可以投影至该像素上。只有当P 的深度确定时（比如通过双目或RGB-D 相机），我们才能确切地知道它的空间位置。
测量像素距离（或深度）的方式有很多种，像人眼就可以根据左右眼看到的景物差异（或称视差）来判断物体与我们的距离。双目相机的原理亦是如此。通过同步采集左右相机的图像，计算图像间视差，来估计每一个像素的深度。下面我们简单讲讲双目相机的成像原理（图5-6 ）。


RGB-D相机：物理手段测量深度

• ToF或结构光两种主要原理
• 通常能得到与RGB图对应的深度图
  

实践部分

注意：先别安装4,后面会讲原因。
本章需要安装OpenC