《视觉SLAM十四讲第二版》笔记及课后习题（第七讲）

最新推荐文章于 2023-03-14 18:42:57 发布

nullwh

最新推荐文章于 2023-03-14 18:42:57 发布

阅读量4.3k

点赞数 9

分类专栏：视觉SLAM十四讲学习笔记

本文链接：https://blog.csdn.net/weixin_43619346/article/details/103213752

版权

本文为《视觉SLAM十四讲第二版》第七讲的读书笔记，主要探讨基于特征点的视觉里程计算法，包括特征点提取、匹配、2D-2D对极几何、3D-2D PnP、3D-2D ICP等问题。实践中使用OpenCV实现特征点提取和匹配，通过实验数据展示ORB特征点的提取和匹配速度。课后习题涉及特征点类型、优化方法、避免误匹配策略等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

读书笔记：视觉里程计1

之前的内容，介绍了运动方程和观测方程的具体形式，并讲解了以非线性优化为主的求解方法。从本讲开始，我们结束了基础知识的铺垫，开始步入正题：按照第二讲的内容，分别介绍视觉里程计、优化后端、回环检测和地图构建四个模块。本讲和下一讲主要介绍作为视觉里程计的主要理论，然后在第九章中进行一次实践。本讲关注基于特征点方式的视觉里程计算法。我们将介绍什么是特征点，如何提取和匹配特征点，以及如何根据配对的特征点估计相机运动。

特征点法

经典SLAM模型中以位姿——路标（Landmark）来描述SLAM过程
- 路标是三维空间中固定不变的点，能够在特定位姿下观测到
- 数量充足，以实现良好的定位
- 较好的区分性，以实现数据关联
在视觉SLAM中，可利用图像特征点作为SLAM中的路标

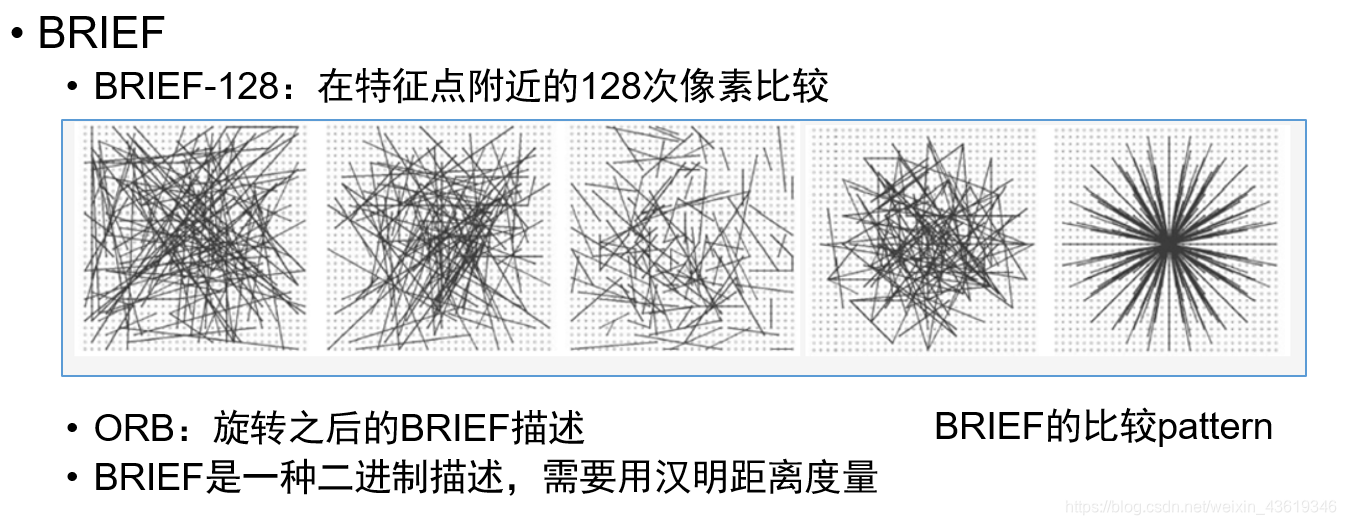
在这里插入图片描述

2D-2D: 对极几何

特征匹配之后，得到了特征点之间的对应关系：

如果只有两个单目图像，得到2D-2D间的关系 ——对极几何
如果匹配的是帧和地图，得到3D-2D间的关系 ——PnP
如果匹配的是RGB-D图，得到3D-3D间的关系 ——ICP

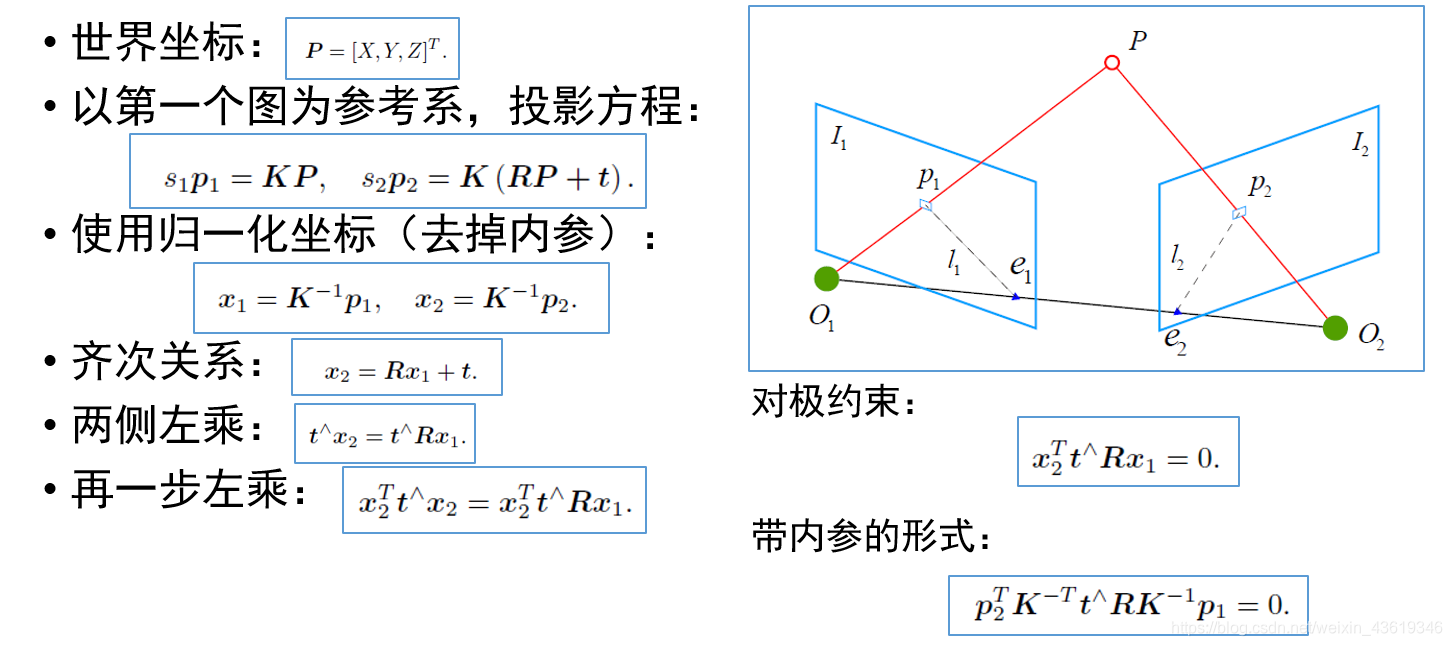
八点法的讨论：
尺度不确定性：归一化 t 或特征点的平均深度
纯旋转问题：t=0 时无法求解
多于八对点时：最小二乘
有外点时：RANSAC

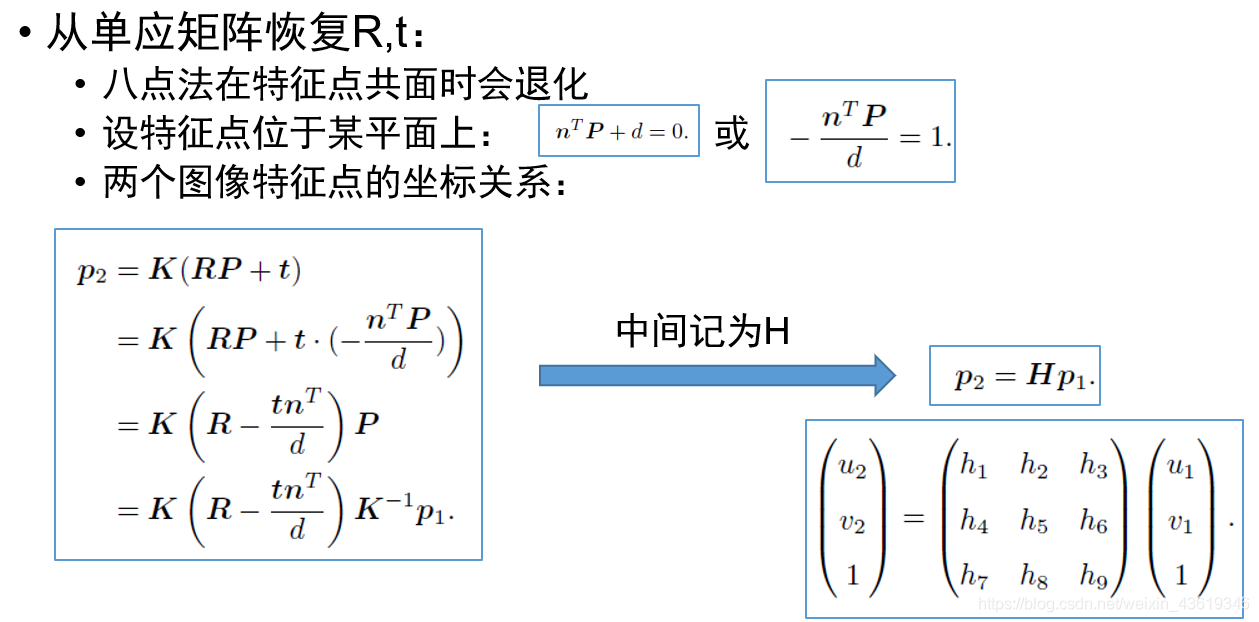
小结：

2D-2D情况下，只知道图像坐标之间的对应关系
- 当特征点在平面上时（例如俯视或仰视），使用H恢复R,t
- 否则，使用E或F恢复R,t
- t 没有尺度
求得R,t后：
- 利用三角化计算特征点的3D位置（即深度）
实际中用于单目SLAM的初始化部分

3D-2D PnP

在这里插入图片描述

3D-2D ICP

在这里插入图片描述

三角化与深度估计

在这里插入图片描述

小结：
本节介绍了基于特征点的视觉里程计中的几个重要的问题。包括：

特征点是如何提取并匹配的；
如何通过2D-2D 的特征点估计相机运动；
如何从2D-2D 的匹配估计一个点的空间位置；
3D-2D 的PnP 问题，它的线性解法和Bundle Adjustment 解法；
3D-3D 的ICP 问题，其线性解法和Bundle Adjustment 解法。

实践部分

orb_cv：

和之前几章一样，导入相应的图片参数后运行代码即可：

/home/wh/shenlan/slambook2/ch7/cmake-build-debug/orb_cv /home/wh/shenlan/slambook2/ch7/1.png /home/wh/shenlan/slambook2/ch7/2.png
extract ORB cost = 0.222814 seconds. 
match ORB cost = 0.000989399 seconds. 
-- Max dist : 95.000000 
-- Min dist : 7.000000

在这里插入图片描述

orb_self：

需要注意一下配置文件（~~通过之前的各种错误调试，对这个已经驾轻就熟了（逃~~ ）：
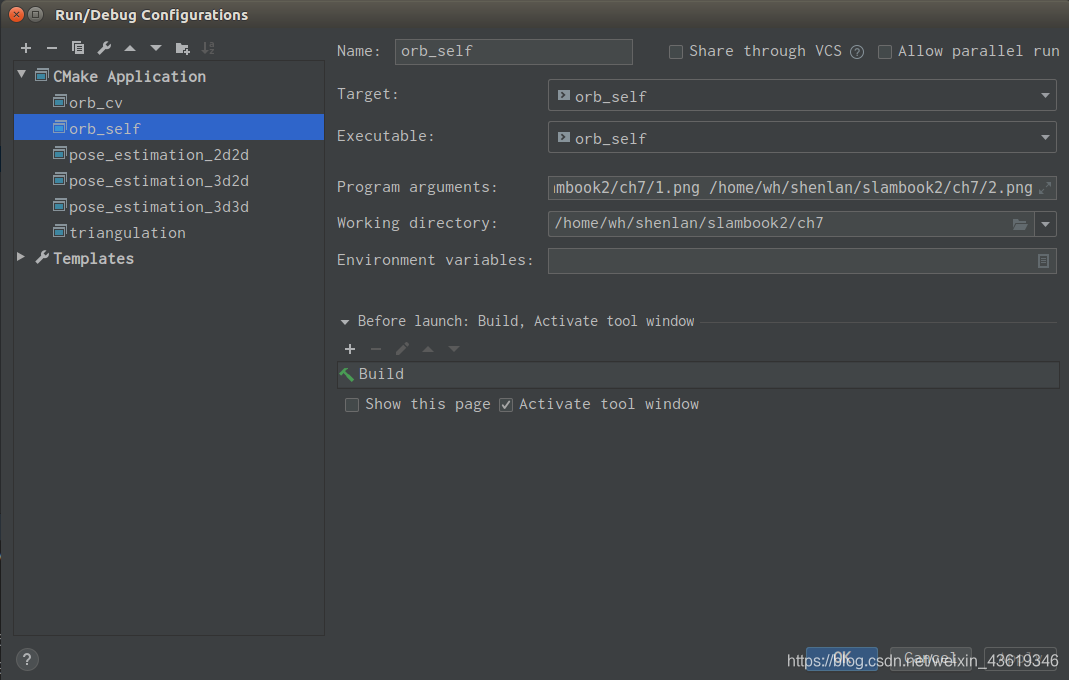
在这里插入图片描述
运行后结果为：

/home/wh/shenlan/slambook2/ch7/cmake-build-debug/orb_self /home/wh/shenlan/slambook2/ch7/1.png /home/wh/shenlan/slambook2/ch7/2.png
bad/total: 43/638
bad/total: 8/595
extract ORB cost = 0.00240357 seconds. 
match ORB cost = 0.000984295 seconds. 
matches: 51

在这里插入图片描述
可见，这个程序中，ORB的提取只要2.4毫秒，匹配只需要0.98毫秒。提升效果还是很明显的。

pose_estimation_2d2d：

导入正确的图片位置参数即可，运行结果如下：

/home/wh/shenlan/slambook2/ch7/cmake-build-debug/pose_estimation_2d2d /home/wh/shenlan/slambook2/ch7/1.png /home/wh/shenlan/slambook2/ch7/2.png
-- Max dist : 95.000000 
-- Min dist : 7.000000 
一共找到了81组匹配点
fundamental_matrix is 
[5.435453065896191e-06, 0.0001366043242983499, -0.02140890086929781;
 -0.0001321142229818118, 2.339475702766975e-05, -0.006332906454914053;
 0.02107630352186664, -0.003666833952417687, 1]
essential_matrix is 
[0.007841371796261635, 0.2075176016541406, 0.1181719698273573;
 -0.190270235105878, 0.03346203071185214, -0.6710910536624433;
 -0.07512093110340777, 0.6702181417805779, 0.0197271235906156]
homography_matrix is 
[0.9131751791765326, -0.1092435315745437, 29.95860009812312;
 0.02223560352253669, 0.9826008005030865, 6.50891083922104;
 -0.000100156038109612, 0.0001037779436268401, 1]
R is 
[0.9980704024700457, -0.05457644989749674, 0.02961220744670522;
 0.05354481493884546, 0.9979665375218761, 0.03457951387400768;
 -0.03143921924039243, -0.03292720916178488, 0.9989631496658776]
t is 
[-0.9411804751897357;
 -0.1569351957186449;
 0.2992501586739325]
t^R=
[-0.01108937434188349, -0.293474206690423, -0.1671204024221927;