8. An Efficient Framework for Clustered Federated Learning

Summary：

0. Three questions

• 文章在解决什么问题?

  现实世界中各个数据参与者拥有的数据大都是 non-IID 的，为了在此基础上训练更高效的联邦学习模型。

  对应联邦学习中主要挑战之一：处理数据分布中的异质性

• 用了什么方法 (创新方法) ?

  现有的解决思路：

  ​ 聚类联邦学习( clustered federated learning )：用户被划分到不同的集群(用户组)。不同的用户组有自己的目标(学习任务)，通过将用户的数据与同一集群中的其他用户聚合(相同的学习任务)，从而可以利用数量上的优势，执行更高效的联邦学习。

  ​ 聚类联邦学习不是建模 non-IID 数据的唯一方法。问题的性质不同，不同的算法可能更适合不同的应用场景。

  本文提出的方法：

  ​ 迭代联邦聚类算法( Iterative Federated Clustering Algorithm，IFCA )，该算法主要思想：交替 estimates the cluster identities of each worker machine(估计用户的聚类身份)、optimizes model parameters for the user clusters via gradient descent 通过梯度下降优化用户聚类的模型参数(最小化损失函数)。

• 效果如何？

  （1）可以放宽对初始化的要求。对于线性模型，即使通过 random initialization and multiple restarts ，算法2 也能收敛。

  （2）算法在 non-convex 非凸损失函数 (eg. 神经网络) 上是有效的。

• 我们的工作

  • 分析该算法 在具有平方损失的线性模型中的收敛速度，分析 在一般的强凸和光滑损失函数的收敛速度。

    证明了在这两种情况下，只要初始化良好，

    • IFCA 就能保证指数级收敛
    • 能够获得接近最优的统计错误率

    我们的工作是第一个描述 clustered FL problems 的收敛行为和统计最优性。

  • 对于有两个 clusters 的线性模型，只要初始化略好于随机，就可以保证我们的算法收敛

  • 当 clustering structure 不明确时，我们将 IFCA 与 多任务学习中的权值共享技术 相结合来训练模型。更具体地，我们使用来自所有用户的数据来训练 共享表示层(shared representation layers)，并使用 IFCA 为每个单独的 cluster 训练 最终层(final layers)

• 在此基础上我的想法

  • first article （只使用 model averaging）

    • 每次迭代时，不随机选择 worker machine 的子集（个数太随机啦，不确定每轮次有多少 worker machines啦），而是使用全部 worker machines（或者使用 C 来控制 worker machines 的数量）。（计算任务主要分布在 worker machines，所以对 center machine 的计算量影响不大）

    • LocalUpdate 函数改为对本地数据进行 B减小、E增加。（增加本地计算量，使得达到目标精度所需的通信次数减小）

      C：每一轮次参与计算的客户端比例数

      B：用于客户端更新的本地小批量大小

      E：每一轮次每个客户端训练本地数据的遍数

    • 梯度裁剪（使得上传的梯度变小，但同时对收敛速度影响不大）

    • 不需要每轮都计算 cluster identity，两轮计算一次呢(不太行)

  • second article（只使用 model averaging）

    • gradient averaging 中 worker machine 上传 gradient 时可以加 差分隐私（原因：直接上传 gradient 容易泄露隐私。属于 模型更新传输阶段的数据泄漏）
    • model averaging 中 worker machine 上传 $\widetilde{{\theta }_i}$ 时会遭到模型反演(逆推)攻击，应添加对应的保护措施（暂时不知道如何保护模型。属于 模型更新传输阶段的数据泄漏）

1. Introduction

用户之间的异质性具有潜在价值：

• 每台机器本身可能没有足够的数据，因此我们需要更好地利用用户之间的相似性（扩大训练模型的数据集）
• 如果我们将所有用户的数据作为 IID 样本，我们无法提供个性化预测

 

思路：将用户划分到不同的 clusters，我们的目标是为每个 cluster 训练模型。

主要挑战：users 的 cluster identities 是未知的

 

待解决问题：

• identifying the cluster membership of each user（estimates the cluster identities of each worker machine）
• optimizing each of the cluster models in a distributed setting

 

2. Related Work

Mansour¹ 提出用 clustered FL 解决联邦学习中的个性化问题。本文提出的算法与 Mansour 提出的算法类似。

本文的主要贡献是在良好的初始化条件下建立了 population loss function (总体损失函数) 的 convergence rate (收敛速度)，同时保证了 convergence of the training loss 和 测试数据的泛化性。而 Mansour 只提供了泛化保证。

 

[1] Three approaches for personalization with applications to federated learning.

 

2.1 Federated Learning and Non-I.I.D. Data

2.2 Latent Variable Problems

 

3. Problem Formulation

假设有 $k$ 个不同的数据分布 $D_1，...,D_k$ ， $m$ 台机器被划分为 $k$ 个不相连的簇 $S_1^{\ast }，...,S_k^{\ast }$ 。

假设不知道每台机器的 cluster identity。假设每个 worker machine $i\in S_j^{\ast }$ 有 $n$ 个 $i.i.d$ data points $z^{i,1}，...,z^{i,n}$ 均属于一个 $D_j$。

其中，每个 data point $z^{i,l}$ 由 a pair of feature and response 组成，即 $z^{i,l}=（x^{i,l},y^{i,l}）$ 。

$z^{i,l}$ ：第 $i$ 个 work machine 的第 $l$ 个 data point

 

目标：最小化 population loss function (一个 cluster 对应一个 $F^j(\theta )$ )
$$F^j(\theta ):=E_{z\sim D_j}[f(\theta ;z)],forallj\in [k]$$

$f(\theta ;z):\Theta \to \mathbb{R}$ 为与 data point (数据点) $z$ 相关的 loss function

E：期望

 

我们把重点放在强凸损失上。该情况下，可以估计（对于每一个 cluster）使得每一个 population loss function 最小的唯一解（可提供证明）。我们尝试找到它们 { θ j ^ } j = 1 k {\{\widehat{\theta_j}\}_{j=1}^k} {θj​ ​}j=1k​ ，他们接近于
$${\theta }_j^{\ast }=argmi{n}_{\theta \in \Theta }{F}^j(\theta ),j\in [k]$$

{ θ j ^ } j = 1 k {\{\widehat{\theta_j}\}_{j=1}^k} {θj​ ​}j=1k​ ：每一个 cluster 最终的 solution

 

由于我们只能访问有限的数据，所有我们使用 empirical loss functions （代替 population loss function）。令 Z ⊆ { z i , 1 ， . . . , z i , n } {Z \subseteq \{z^{i,1}， ..., z^{i,n}\}} Z⊆{zi,1，...,zi,n} 是第 $i$ 台机器上 data points (数据点) 的子集，与 $Z$ 相关的 empirical loss functions 为
$$F_i(\theta ;Z)=\frac{1}{\mid Z\mid }\sum _{z\in Z}f(\theta ;z)$$
我们也可以使用 $F_i(\theta )$ 来表示 第 $i$ 个 worker machine 的 some(or all) data 的 empirical loss functions

 

4. Algorithm

本节中，首先提出 one-shot clustering algorithm ，皆在 在 center machine 上的一轮聚类中 estimate cluster identities of each worker machine 。并讨论了存在的缺陷；

4.2节，提出一种迭代联邦聚类算法，该算法交替 估计用户的聚类身份、通过梯度下降优化用户聚类的模型参数(最小化损失函数)。

 

4.1 One-Shot Clustering（只有一次的聚类）

步骤：

• 每个 worker machine 使用本地数据训练一个模型 $\widetilde{{\theta }_i}$ ，并将 $\widetilde{{\theta }_i}$ 发送给 center machine
• center machine 通过 在 $\widetilde{{\theta }_i}$ 上执行 k-means 来 estimates the cluster identities of each worker machine
• 之后，center machine 在每个 cluster 单独运行任何FL算法，例如 gradient-based methods、Federated Averaging (FedAvg) algorithm、second-order methods

该算法主要缺点：

• 只对 worker machine 进行了一次聚类。如果 clustering algorithm 生成了不正确的 identity estimations ，该算法则没有纠正能力
• 聚类是在 center machine 上完成的，如果 m 很大，则计算量就会很大
• 第一阶段计算局部 empirical risk minimization (ERM，经验风险最小化) 时，只能使用 convex loss functions ，而不能是更复杂的模型，如神经网络。原因：ERM 的解 $\widetilde{{\theta }_i}$ 还会被用于基于距离的聚类算法，如 k-means。对于神经网络，由于模型对隐藏单元的 permutation invariance (置换不变性)，两个相似的模型的参数可能相距很远。

 

4.2 Iterative Federated Clustering Algorithm (IFCA)（迭代联邦聚类算法）

与 one-shot clustering 对比：IFCA 不需要 a centralized clustering algorithm，降低了 center machine 的计算量，即不需要 center machine 执行 k-means

 

IFCA 的两种变体：梯度平均、模型平均

 

(a) server 广播模型

(b) worker machines 识别他们的 cluster memberships 并执行 local updates

© worker machines 将本地模型发给 server

(d) 对 same estimated cluster $S_j$ 中的模型进行平均

 

步骤：

center machine 生成 $k$ 个初始模型参数 ${\theta }_j^{(0)},j\in [k]$ 。

在 IFCA 第 $t$ 次迭代中，center machine 选择 worker machines 的一个随机子集 $M_t\subseteq [m]$ ，并广播当前模型参数 { θ j ( t ) } j = 1 k {\{\theta^{(t)}_j\}_{j=1}^k} {θj(t)​}j=1k​ 给 $workermachine\in M_t$ 。

{ θ j ( t ) } j = 1 k {\{\theta^{(t)}_j\}_{j=1}^k} {θj(t)​}j=1k​ ：在第 $t$ 次迭代时，将参数 ${\theta }_j$ 广播给 $M_t$

每一个 worker machine 都有 local empirical loss functions $F_i(\cdot )$ ，使用接收到的 parameter estimate 和 $F_i$ ，第 $i,i\in M_t$ 个 worker machine 通过找到损失最小的模型参数来 estimates its cluster identities，eg. $\hat{j}=argmi{n}_{j\in [k]}{F}_i({\theta }_j^{(t)})$。

• 如果我们选择梯度平均，

  • worker machine 然后需要计算 local empirical loss $F_i$ 在 ${\theta }_{\hat{j}}^{(t)}$ 上的(随机)梯度，并 将其 cluster identity estimate and gradient 发送给 center machine 。
  • 在接收到来自所有 $M_t$ 的 cluster identity estimate and gradient 后，center machine 收集（ 来自 cluster identity estimate 相同的所有 的 $workermachine\in M_t$ ）梯度更新，并对相应 cluster 的模型参数执行梯度下降更新。

• 如果我们选择模型平均(similar to FedAvg)，

  • 每个 $workermachine\in M_t$ 需要运行 $\tau$ 次 local(随机)梯度下降更新以获得更新的模型。并 将新的模型和 its cluster identity estimate 发送给 center machine 。
    • 然后 center machine 对 （ 来自 cluster identity estimate 相同的所有 $workermachine\in M_t$ 的） 新模型求平均值。

 

 

4.3 Practical Implementation of IFCA（IFCA 的实施工作；结合多任务学习，没有读懂）

 

分析一下算法存在的问题(本地的计算量太大、通信次数会不会太多、存在的隐私问题)

存在的问题：

​ 在一些实际问题中，cluster structure 可能是模糊的，这意味着来自不同 cluster 的数据分布是不同的，但 用户的数据之间存在一些共同的属性，模型应该利用这些属性。

 

解决思路：

​ 将多任务学习中的权值共享技术，与 IFCA 结合。

​ 更具体地，当我们训练神经网络模型时，在所有 cluster 之间共享前几层的权重（以便我们可以使用所有数据学习一个 good representation，共享表示层(shared representation layers) ），然后只在最后一层（或最后几层）上运行 IFCA 算法（以解决不同聚类之间的不同分布，最终层(final layers) ）。

具体实现：

​ 我们在 the coordinates of ${\theta }_j^{(t)}$ 的子集上运行 IFCA，并在剩余的 coordinates 运行 vanilla(普通的) gradient or model averaging 。该方法的另一个好处是 可以降低通信成本：center machine 不需要向所有 worker machines 发送 $k$ 个模型，只需要发送 $k$ different versions of a subset of all the weights，以及 shared layers 的 one single copy。

​

​ 另一种降低通信成本的技术是：当 center machine 观察到所有 worker machines 的 cluster identities 是稳定的（即：它们的 estimates cluster identities 在几次的并行迭代中都没有发生变化 ），那么 center machine 可以不再每次都向每个 worker machine 发送 $k$ 个模型，而是直接发送与该 worker machine 对应的 cluster 的模型（仅有1个模型）。

 

5. Theoretical Guarantees (理论保证)

 

5.1 Linear Models with Squared Loss (平方损失的线性模型)

分析 IFCA 在具有平方损失的线性模型中的收敛速度

 

5.2 Strongly Convex Loss Functions (强凸损失函数)

分析在一般的强凸和光滑损失函数的收敛速度。

 

6. Experiments (实验)

我们没有在每次迭代中都重新采样新的数据点

 

6.1 Synthetic Data (合成数据)

​ 首先评估 算法2 的 gradient averaging (option I) 在线性模型上的平方损失。

​ 对于 $allj\in [k]$ ，首先生成 ${\theta }_j^{\ast }\sim Bernoulli(0.5)$ coordinate-wise（坐标态），然后将他们的 $l_2$ 范数重新缩放到 $R$ 。这确保 the separation between the ${{\theta }_j^{\ast }s}^{’}$ 与 $R$ in expectation( $R$ 的期望) 成正比。在实验中，使用 $R$ 表示 { θ j } j = 1 k {\{{\theta_j}\}_{j=1}^k} {θj​}j=1k​ （ground truth 参数向量）之间的 $separation$ 。此外，我们模拟了如下场景：所有的 worker machines 参与所有的 iterations，并且 所有的 clusters 包含相同数量的 worker machines。在每次实验中，我们首先生成 ${{\theta }_j^{\ast }s}^{’}$ 参数向量，将他们固定。然后根据一个独立的 coordinate-wise Bernoulli distribution 随机初始化 ${\theta }_j^{(0)}$ 。然后我们迭代 300 次算法2（step size 不变，即学习率不变）。

​ 当 k=2、k=4 时，我们分别选择步长为 { 0.01, 0.1, 1 }、{ 0.5, 1.0, 2.0 } 。为了确保我们是否成功地学习了模型，我们 sweep over(遍历) 前面提到的步长，并定义了以下的距离度量 $dist=\frac{1}{k}{\sum }_{j=1}^k\mid \mid \widehat{{\theta }_j}-{\theta }_j^{\ast }\mid \mid$ ，其中 { θ j ^ } j = 1 k {\{\widehat{\theta_j}\}_{j=1}^k} {θj​ ​}j=1k​ 是从算法2获得的参数估计。对于一个 ${\theta }_j^{\ast }$ 的固定集合，在10个随机初始化的 ${\theta }_j^{(0)}$ 中 ，至少有一个使得 $dist\le 0.6\sigma$ （$\sigma$：noise parameter for synthetic data generation），则试验被认为是成功的。

 

 

​ (a-b) 中，绘制了关于 $R$ 的40次 empirical success probability 。(a) 中 设置的参数为 (m, n, d) = (100, 100, 1000)、k=2，(b) 中 设置的参数为 (m, n, d) = (400, 100, 1000)、k=4。观察可知，当 $R$ 变大时（即：参数 { θ j } j = 1 k {\{{\theta_j}\}_{j=1}^k} {θj​}j=1k​ 之间的间隔增大），问题更容易解决，可获得更高的成功率。这验证了我们的理论：较高的信噪比产生较小的误差下限。

m：number of machines

n：number of datapoints for each machine

d：dimension of the datapoint 数据点的维度

 

​ (c-d) 中，描述了 m 与 n 的依赖关系。© 中 固定 (R, d) = (0.1, 1000)、(d) 中 固定 (R, d) = (0.5, 1000)。观察可知，当增大 m 或 n 时，成功率提高。这验证了我们的理论：更多的数据或更多的 worker machines 有助于提高算法的性能。

 

6.2 Rotated MNIST and CIFAR (旋转 MNIST 和 旋转 CIFAR)

介绍实验数据：

​ 为了模拟环境：不同 worker machine 上的数据从不同的分布生成，我们使用 rotation(旋转) 来增强数据集，创建了 Rotated MNIST 和 Rotated CIFAR 数据集。

• 对于 Rotated MNIST ，首先 对图像进行 0，90，180，270 度的旋转来增强数据集，从而得到 $k=4clusters$ 。 对于给定的 m、n 满足 mn=60000k，我们将图像随机划分给 $m$ 个 worker machines，保证每台机器保留 $n$ 张图像（相同的旋转角度）；我们以同样的方式将测试数据分到 $m_{test}=10000k/n$ 个 worker machines 上。
• Rotated CIFAR 以与 Rotated MNIST 类似的方式创建，主要区别在于： 对图像进行 0,180 度的旋转来增强数据集，从而得到 $k=2clusters$ 。

 

介绍实验模型：

​ 在 MNIST 实验中，使用具有 ReLU 激活的全连接神经网络，其中单个隐藏层大小为200；

​ 在 CIFAR 实验中，使用 由2个卷积层和2个全连接层组成的卷积神经网络，并对图像进行了标准数据增强处理，eg. 翻转、随机裁剪等的。

 

算法对比：

• 将 IFCA model averaging (option II) 与 two baseline algirithm（global model、local model） 比较。

  • 对于 MNIST 实验，所有 worker machines（$M_t=[m]forallt$） 均参与训练。在 LocalUpdate 中，选择 $\tau =10、stepsize\gamma =0.1$ 。
  • 对于 CIFAR 实验，我们选择 $\mid M_t\mid =0.1m$ 并应用 step size 衰减 0.99。在 LocalUpdate 中，选择 $\tau =5、batchsize=50$ 。

• 在 global model 中，算法尝试学习单个全局模型，使得能对所有的分布做出预测。该算法不考虑 cluster identities ，所以算法1 中的模型平均修改为 ${\theta }^{(t+1)}={\sum }_{i\in M_t}\frac{\widetilde{{\theta }_i}}{\mid M_t\mid }$ ，即对所有参与训练的 machines 进行 参数平均。

• 在 local model 中，每个 machines 只对本地数据进行梯度下降，不进行模型平均。

对于 IFCA 和 global model 方案，我们采用以下方式进行 inference (推理)。对于每一台 test worker machine，我们对学习到的模型（IFCA 的 k 个模型和 global model 的1个模型）进行 inference (推理)，并对 smallest loss value 的模型计算精度。为了测试 local model baselines，通过 measure 具有相同分布（相同旋转角度）的 test data 的精度来 test 模型。我们汇报了 worker machines 中所有模型的平均精度。对于所有的算法，我们使用5种不同的随机种子进行实验，汇报了平均值和标准差。

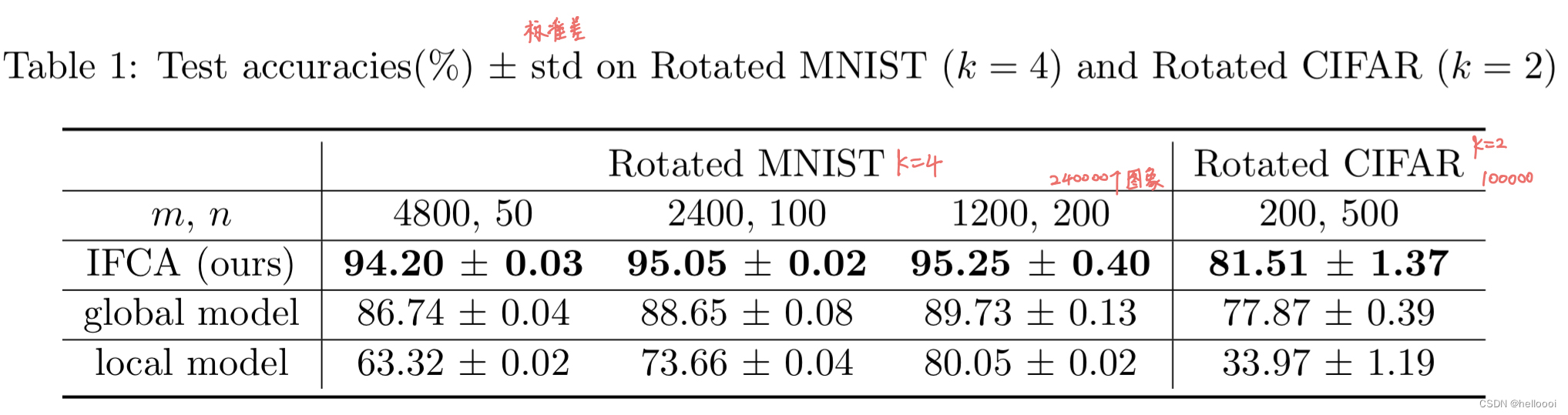
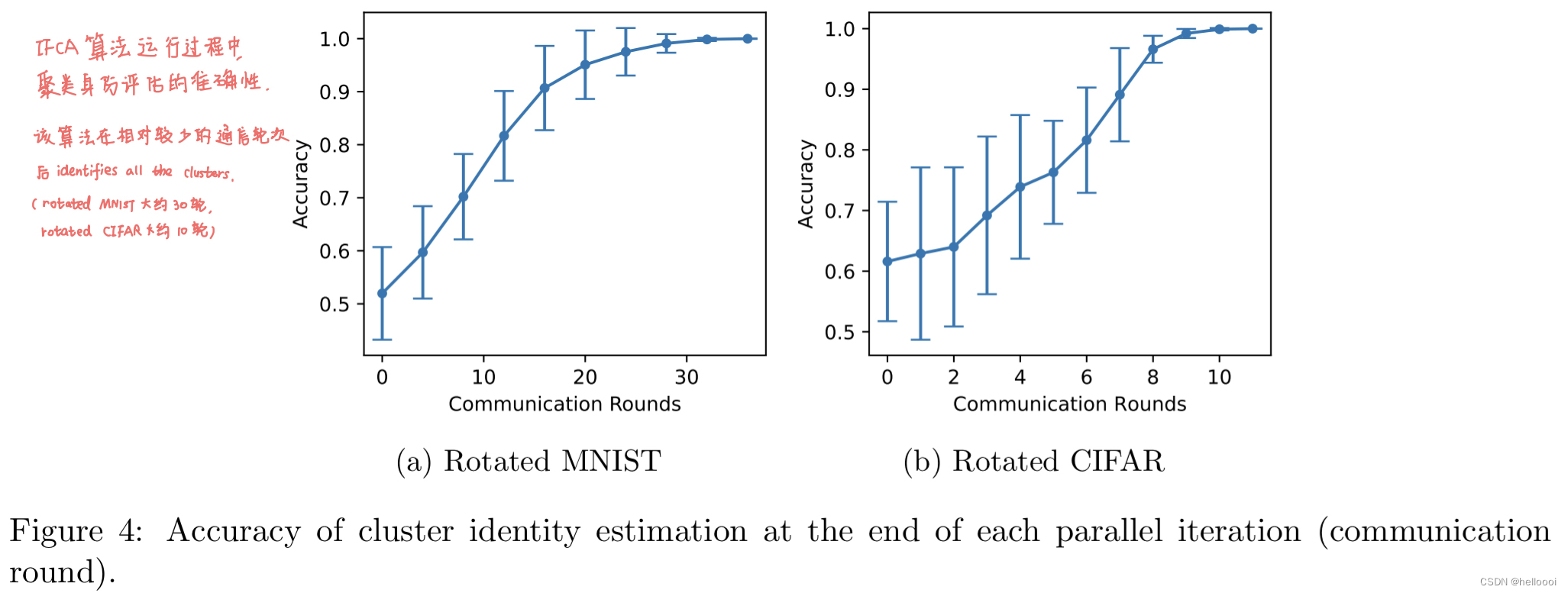
算法对比：

​ 运行 IFCA 时，可以观察到 算法可以逐渐找到 worker machines 的 underlying cluster identities (正确的 cluster id) ，并且在找到正确的集群后，使用具有相同分布的数据对每个模型进行训练和测试，可以获得更好的准确性。

​ global model 的表现比我们差，因为它试图拟合来自不同分布的所有数据，并不能提供个性化预测。

​ local model 容易对 local data 过拟合，导致性能不如我们的算法。
 

6.2 Federated EMNIST (使用到 权重共享技术，没看懂)

​ Federated EMNIST (FEMNIST) 是一个 realistic (现实的) 数据集，其中每一个 worker machine 上的数据点来自于一个 specific writer 的手写数字或字母。虽然所有用户之间的数据分布是相似的，但由于不同人的 writing styles 可能被聚类，因此可能存在 ambiguous cluster structure (模糊的聚类结构) 。

​ 我们使用 4.3节中 提到的 权值共享技术 。我们用一个有2个卷积层的神经网络，在每个卷积层后有一个 max pooling layer，然后是两个全连接层。我们共享所有层的权重（除了由 IFCA 训练的最后一层的权重）。我们将 cluster 的数量 k 作为一个超参数，并以不同的 k 运行实验。

 

• IFCA 比 global model 和 local model 有明显的优势。

• IFCA 与 one-shot 的结果相似，但 IFCA 不运行集中式聚类过程，降低了 center machine 的计算成本。

• IFCA 对 cluster的数量 k 具有鲁棒性。当 k=2、k=3 时，算法的结果相似。我们还注意到，当 k>3 时，IFCA 自动识别 3 clusters，其余的 cluster 为空。这表名 IFCA 在 cluster structure is ambiguous and the number of clusters is unknown 的现实问题中具有更强的适用性。