最小频移键控 Minimum shift keying(MSK)
最近需要学习MSK,在论坛上看了很多篇文章仍然是云里雾里,倒腾了好多天终于稍微弄清楚了点MSK的调制部分,所以写了这篇浅入浅出的学习笔记。主要参考的是Marvin K.Simon的《Bandwidth-Efficient Digital Modulation with Application to Deep-Space Communications》中前两章部分;欢迎大家指正。
一、 MSK的CPM调制
1.连续相位调制CPM与MSK的关系
Continuous phase modulation(CPM)通过改变载波的相位来反应原信号信息,按调制频率脉冲是一个比特时间还是更长分为全响应和部分响应。全响应中,调制指数h=0.5,任意频率脉冲的为广义MSK。若频率脉冲为一个矩形频率脉冲,则为MSK,若是升余弦,则为sinusodial frequency-shift-keying (SFCK)。而调制指数任意但频率脉冲为矩形的是continuous phase frequency pulse (CPFSK),此时若调制指数为0.5,则又成为了MSK。部分响应中,以Gaussian minimum-shift-keying(GMSK)最为常见,事实上,在进行MSK调制前将矩形信号脉冲先通过一个高斯型的低通滤波器即可得到GMSK。整个关系在全响应那里有点绕,尝试用markdown的mermaid流程图阐述一下我理解的关系:
2.Continuous Phase Frequency Modulation Representation (CPFM)
下面进行MSK的CPM调制的数学推导:一个具有连续包络波形的二进制单模CPM信号通式为:
s
(
t
)
=
2
E
b
T
b
c
o
s
(
2
π
f
c
t
+
ϕ
(
t
,
α
)
+
ϕ
0
)
,
n
T
b
≤
t
≤
(
n
+
1
)
T
b
(
1
)
s(t) = \sqrt{\frac{2E_b}{T_b}} cos(2\pi f_ct+\phi(t,\alpha)+\phi_0), \qquad nT_b\leq t \leq (n+1)T_b \quad(1)
s(t)=Tb2Ebcos(2πfct+ϕ(t,α)+ϕ0),nTb≤t≤(n+1)Tb(1) 其中。Eb和Tb分别是一个比特的能量和持续时间,fc是载波频率,
ϕ
0
\phi_0
ϕ0是初始相位,可以取0.而
ϕ
(
t
,
α
)
\phi(t,\alpha)
ϕ(t,α)即是相位调制过程(瞬时相位偏移随m(t)作线性变化),可表示为:
ϕ
(
t
,
α
)
=
2
π
∑
i
≤
n
α
i
h
q
(
t
−
i
T
b
)
(
2
)
\phi(t,\alpha)=2\pi\sum_{i\leq n} \alpha_ihq(t-iT_b)\qquad (2)
ϕ(t,α)=2πi≤n∑αihq(t−iTb)(2)
α
\alpha
α是独立同分布(i.i.d)的二进制序列,相等概率地取
±
1
\pm 1
±1,h为调制指数,q(t)为归一化平滑相应(the normalized phase-smoothing response),也就是说,q(t)决定了基本相位(the underlying phase)
2
π
α
i
h
2\pi\alpha_ih
2παih是如何变化的;同时,我们定义q(t)的导数g(t)为第零时刻的信号间隔内产生的瞬时频率脉冲:
g
(
t
)
=
d
q
(
t
)
d
t
(
3
)
g(t)=\frac{dq(t)}{dt}\qquad (3)
g(t)=dtdq(t)(3) 因此,q(t)可以由g(t)积分得到:
q
(
t
)
=
∫
−
∞
t
g
(
τ
)
d
τ
(
4
)
q(t)=\int_{-\infty}^t g(\tau)d\tau \qquad (4)
q(t)=∫−∞tg(τ)dτ(4) 由于对于MSK,g(t)是一个矩形脉冲,
T
b
T_b
Tb内积分面积为
1
2
\frac12
21 ,且g(t)仅在比特时间间隔内不为0 (g(t) is nonzero only over the bit interval) ,因此q(t)其实是满足下面这个式子的:
q
(
t
)
=
{
0
,
t
≤
0
1
2
,
t
≥
T
b
(
5
)
q(t) =\begin{cases}0, & t \leq 0 \\\frac12, & t\geq T_b\end{cases} \qquad(5)
q(t)={0,21,t≤0t≥Tb(5) 从(5)式可以看出,第i个数据
α
i
\alpha_i
αi对在
T
b
T_b
Tb时间后对整个相位有
π
α
i
h
\pi\alpha_ih
παih的贡献,这种被修正后的相位变化会持续到之后的所有时间。由于这种相位平滑响应上的重叠,每个信号间隔内的总想为是当前数据和之前所有数据的函数,因此我们说MSK的CPM调制是具有记忆性的,最佳的解调方式是最大似然序列分析(Maximum-likelihood sequence estiymator) 对于g(t),可以由下式来描述:
g
(
t
)
=
{
1
2
T
b
,
0
≤
t
≤
T
b
0
,
o
t
h
e
r
w
i
s
e
(
6
)
g(t) =\begin{cases}\frac{1}{2T_b}, & 0\leq t \leq T_b \\0, & otherwise\end{cases} \qquad(6)
g(t)={2Tb1,0,0≤t≤Tbotherwise(6) 那么由(4)式定义得到的相位脉冲即为:
q
(
t
)
=
{
t
2
T
b
,
0
≤
t
≤
T
b
1
2
,
t
≥
T
b
(
7
)
q(t) =\begin{cases}\frac{t}{2T_b}, & 0\leq t \leq T_b \\\frac12, & t \geq T_b\end{cases} \qquad(7)
q(t)={2Tbt,21,0≤t≤Tbt≥Tb(7) g(t)和q(t)的函数图像如下表示,可以看出q(t)其实是无限延伸的。

现在,结合 h=0.5 和g(t)表达式,我们可以得到MSK的CPM调制表达式:
s
M
S
K
(
t
)
=
2
E
b
T
b
c
o
s
(
2
π
f
c
t
+
π
2
T
b
∑
i
≤
n
α
(
t
−
i
T
b
)
)
,
n
T
b
≤
t
≤
(
n
+
1
T
b
)
(
8
)
s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}cos(2\pi f_ct+\frac{\pi}{2T_b}\sum_{i\leq n}\alpha(t-iT_b) ),\quad nT_b\leq t \leq (n+1T_b) \qquad(8)
sMSK(t)=Tb2Ebcos(2πfct+2Tbπi≤n∑α(t−iTb)),nTb≤t≤(n+1Tb)(8) 为了更直观地理解MSK的相位变化,给出其相位树:
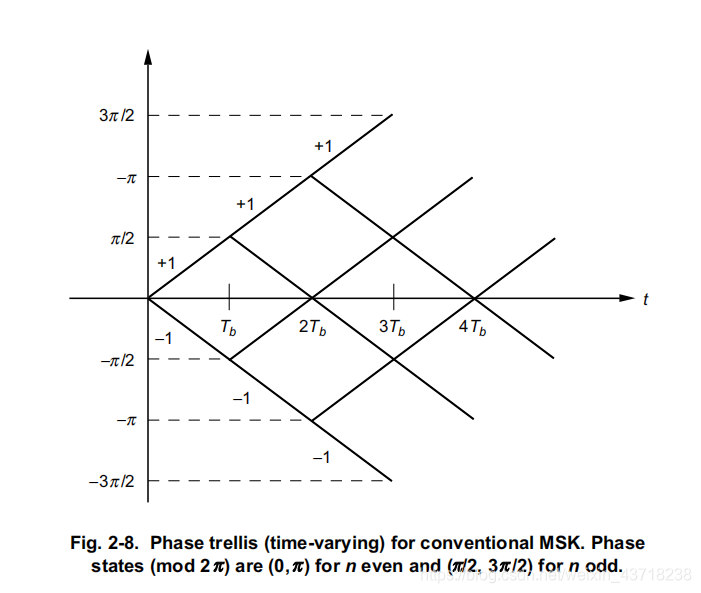
可以看出,MSK随时间的相位变化是线性的,其相位树上的路径是斜率为 ± π 2 T b \pm \frac{\pi}{2}T_b ±2πTb的直线。每个比特时间的相位变化根据 α i \alpha_i αi的极性来决定是 π 2 \frac{\pi}{2} 2π还是 − π 2 -\frac{\pi}{2} −2π。且在模2 π \pi π的体系下,其偶数时刻的相位是0或 π \pi π,奇数时刻的相位是 π 2 \frac{\pi}{2} 2π或 3 π 2 \frac{3\pi}{2} 23π.
二、MSK的正交表示
由于记忆性,CPM需要采用如最大似然序列分析(MLSE)的解调方式,而像MSK这样调制指数h=0.5的全响应调制实际上可以进行无记忆性的I-Q接收。因为MSK调制的发射可以用类似于OQPSK的I-Q形式执行。
1.Equivalent I-Q Representation of MSK
下面进行MSK正交表达式的数学推导: 改写(8)式里第n个信号间隔里MSK信号的附加相移为: ϕ ( t , α ) = π 2 T b ∑ i ≤ n α i ( t − i T b ) = α n π 2 T b ( t − n T b ) + π 2 ∑ i ≤ n − 1 α i = α n π 2 T b t + x n , \phi(t,\alpha)=\frac{\pi}{2T_b}\sum_{i\leq n} \alpha_i(t-iT_b)=\alpha_n\frac{\pi}{2T_b}(t-nT_b)+\frac\pi2 \sum_{i\leq n-1} \alpha_i=\alpha_n\frac{\pi}{2T_b}t+x_n, ϕ(t,α)=2Tbπi≤n∑αi(t−iTb)=αn2Tbπ(t−nTb)+2πi≤n−1∑αi=αn2Tbπt+xn, n T b ≤ t ≤ ( n + 1 ) T b ( 11 ) nT_b\leq t\leq (n+1)Tb\qquad\qquad(11) nTb≤t≤(n+1)Tb(11)其中 π 2 ∑ i ≤ n − 1 α i \frac\pi2 \sum_{i\leq n-1} \alpha_i 2π∑i≤n−1αi是第n个时间间隔开始时的累积相位。 x n x_n xn是使 t = n T b t=nT_b t=nTb和 t = ( n + 1 ) T b t=(n+1)T_b t=(n+1)Tb处码元相位连续的相位常数,同时其也是模 2 π 2\pi 2π的附加相位图路径上的y轴截距。前一个时间间隔的附加相移为: ϕ ( t , α ) = α n π 2 T b ( t − ( n − 1 ) T b ) + π 2 ∑ i ≤ n − 2 α i = α n − 1 π 2 T b t + x n − 1 , \phi(t,\alpha)=\alpha_n\frac{\pi}{2T_b}(t-(n-1)T_b)+\frac\pi2 \sum_{i\leq n-2} \alpha_i=\alpha_{n-1}\frac{\pi}{2T_b}t+x_{n-1}, ϕ(t,α)=αn2Tbπ(t−(n−1)Tb)+2πi≤n−2∑αi=αn−12Tbπt+xn−1, ( n − 1 ) T b ≤ t ≤ n T b ( 12 ) (n-1)T_b\leq t\leq nTb\qquad\qquad(12) (n−1)Tb≤t≤nTb(12)对比(11)式和(12)式,为使相位在 t = n T b t = n T_b t=nTb处连续,要求: α n π 2 T b ( n T b ) + x n = α n − 1 π 2 T b ( n T b ) + x n − 1 ( 13 ) \alpha_n\frac{\pi}{2T_b}(nT_b)+x_n=\alpha_{n-1}\frac{\pi}{2T_b}(nT_b)+x_{n-1}\qquad(13) αn2Tbπ(nTb)+xn=αn−12Tbπ(nTb)+xn−1(13)即 x n = x n − 1 + π n 2 ( α n − 1 − α n ) ( 14 ) x_n=x_{n-1}+\frac{\pi n}{2}(\alpha_{n-1}-\alpha_n)\qquad (14) xn=xn−1+2πn(αn−1−αn)(14)由该递归式可知在给定初始条件 x 0 x_0 x0的情况下,任何时间间隔内的 x n x_n xn都可以被确定。注意到 ( α n − 1 − α n ) (\alpha_{n-1}-\alpha_n) (αn−1−αn)是一个分别以概率1/2,1/4,1/4取值于0,+1,-1的三元随机变量。因此,由(14)可知,当 α n − 1 = α n \alpha_{n-1}=\alpha_n αn−1=αn时, x n = x n − 1 x_n=x_{n-1} xn=xn−1,当 α n − 1 ≠ α n \alpha_{n-1}\neq\alpha_n αn−1̸=αn时, x n = x n − 1 ± π n x_n=x_{n-1}\pm\pi n xn=xn−1±πn。如果取= 0 ,可以发现在模 2 π 2\pi 2π时取值0或 π \pi π。由(8)和(11),通过三角公式展开,可得: s M S K ( t ) = 2 E b T b ( c o s ϕ ( t , α ) c o s 2 π f c t − s i n ϕ ( t , α ) s i n 2 π f c t ) , n T b ≤ t ≤ ( n + 1 T b ) ) ( 15 ) s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}(cos\phi(t,\alpha)cos2\pi f_ct-sin \phi(t,\alpha)sin2\pi f_ct),\quad nT_b\leq t \leq (n+1T_b) )\qquad(15) sMSK(t)=Tb2Eb(cosϕ(t,α)cos2πfct−sinϕ(t,α)sin2πfct),nTb≤t≤(n+1Tb))(15) 其中 c o s ϕ ( t , α ) = c o s ( α π 2 T b t + x n ) = ± c o s ( α π 2 T b t ) = ± c o s π 2 T b t = a n c o s π 2 T b t , 令 a n = c o s x n = ± 1 cos\phi(t,\alpha)=cos(\alpha\frac{\pi}{2T_b}t+x_n)=\pm cos(\alpha\frac{\pi}{2T_b}t)=\pm cos\frac{\pi}{2T_b}t=a_ncos\frac{\pi}{2T_b}t,令a_n=cosx_n=\pm1 cosϕ(t,α)=cos(α2Tbπt+xn)=±cos(α2Tbπt)=±cos2Tbπt=ancos2Tbπt,令an=cosxn=±1 s i n ϕ ( t , α ) = s i n ( α π 2 T b t + x n ) = ± s i n ( α π 2 T b t ) = ± α s i n π 2 T b t = b n s i n π 2 T b t , 令 b n = α n c o s x n = ± 1 sin\phi(t,\alpha)=sin(\alpha\frac{\pi}{2T_b}t+x_n)=\pm sin(\alpha\frac{\pi}{2T_b}t)=\pm \alpha sin\frac{\pi}{2T_b}t=b_nsin\frac{\pi}{2T_b}t,令b_n=\alpha_n cosx_n=\pm1 sinϕ(t,α)=sin(α2Tbπt+xn)=±sin(α2Tbπt)=±αsin2Tbπt=bnsin2Tbπt,令bn=αncosxn=±1 ( 16 ) \qquad\qquad\qquad\qquad(16) (16)最后用(16)代替(15)可以得到MSK的I-Q形式: s M S K ( t ) = 2 E b T b ( a n C ( t ) c o s 2 π f c t − b n S ( t ) s i n 2 π f c t ) , n T b ≤ t ≤ ( n + 1 ) T b ( 17 ) s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}(a_nC(t)cos2\pi f_ct-b_nS(t)sin2\pi f_ct),\quad nT_b\leq t \leq (n+1)T_b \qquad(17) sMSK(t)=Tb2Eb(anC(t)cos2πfct−bnS(t)sin2πfct),nTb≤t≤(n+1)Tb(17) 其中 C ( t ) = c o s π t 2 T b C(t)=cos\frac{\pi t}{2T_b} C(t)=cos2Tbπt S ( t ) = s i n π t 2 T b S(t)=sin\frac{\pi t}{2T_b} S(t)=sin2Tbπt ( 18 ) \qquad\qquad\qquad\qquad(18) (18)是同相分量(I)和正交分量(Q)的脉冲波形,即二进制数据序列{ a n a_n an},{ b n b_n bn}的正弦型加权函数。
2.MSK信号与FSK的联系
下面通过MSK的I-Q形式来讨论MSK信号与FSK的联系:用积化和差公式对(17)中成分进行变形,得到:
C
(
t
)
c
o
s
2
π
f
c
t
=
1
2
c
o
s
[
2
π
(
f
c
+
1
4
T
b
)
t
]
+
1
2
c
o
s
[
2
π
(
f
c
−
1
4
T
b
)
t
]
S
(
t
)
s
i
n
2
π
f
c
t
=
−
1
2
c
o
s
[
2
π
(
f
c
+
1
4
T
b
)
t
]
+
1
2
c
o
s
[
2
π
(
f
c
−
1
4
T
b
)
t
]
(
19
)
C(t)cos2\pi f_ct=\frac12cos[2\pi(f_c+\frac{1}{4T_b})t]+\frac12cos[2\pi(f_c-\frac{1}{4T_b})t]\\ S(t)sin2\pi f_ct=-\frac12cos[2\pi(f_c+\frac{1}{4T_b})t]+\frac12cos[2\pi(f_c-\frac{1}{4T_b})t]\\ \qquad(19)
C(t)cos2πfct=21cos[2π(fc+4Tb1)t]+21cos[2π(fc−4Tb1)t]S(t)sin2πfct=−21cos[2π(fc+4Tb1)t]+21cos[2π(fc−4Tb1)t](19)代入(17)得:
s
M
S
K
(
t
)
=
2
E
b
T
b
[
(
a
n
+
b
n
2
)
c
o
s
[
2
π
(
f
c
+
1
4
T
b
)
]
+
(
a
n
−
b
n
2
)
c
o
s
[
2
π
(
f
c
−
1
4
T
b
)
]
]
,
n
T
b
≤
t
≤
(
n
+
1
)
T
b
(
20
)
s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}\bigl[(\frac{a_n+b_n}{2})cos[2\pi(f_c+\frac{1}{4T_b})]+(\frac{a_n-b_n}{2})cos[2\pi(f_c-\frac{1}{4T_b})]\bigr],\quad nT_b\leq t \leq (n+1)T_b\qquad(20)
sMSK(t)=Tb2Eb[(2an+bn)cos[2π(fc+4Tb1)]+(2an−bn)cos[2π(fc−4Tb1)]],nTb≤t≤(n+1)Tb(20)因此,当
α
=
1
时
a
n
=
b
n
\alpha=1时a_n=b_n
α=1时an=bn,有
s
M
S
K
(
t
)
=
2
E
b
T
b
c
o
s
[
2
π
(
f
c
+
1
4
T
b
)
t
]
(
21
)
s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}cos[2\pi(f_c+\frac{1}{4T_b})t]\qquad(21)
sMSK(t)=Tb2Ebcos[2π(fc+4Tb1)t](21)此时频率为
f
c
+
1
4
T
b
f_c+\frac{1}{4T_b}
fc+4Tb1.
当
α
=
−
1
时
a
n
=
−
b
n
\alpha=-1时a_n=-b_n
α=−1时an=−bn,有
s
M
S
K
(
t
)
=
2
E
b
T
b
c
o
s
[
2
π
(
f
c
−
1
4
T
b
)
t
]
(
21
)
s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}cos[2\pi(f_c-\frac{1}{4T_b})t]\qquad(21)
sMSK(t)=Tb2Ebcos[2π(fc−4Tb1)t](21)此时频率为
f
c
−
1
4
T
b
f_c-\frac{1}{4T_b}
fc−4Tb1.
即
α
=
1
α= 1
α=1时,MSK信号频率为
f
c
+
1
4
T
b
f_c+\frac{1}{4T_b}
fc+4Tb1,
α
=
−
1
α= -1
α=−1时,MSK信号频率为
f
c
−
1
4
T
b
f_c-\frac{1}{4T_b}
fc−4Tb1;通过信号频率的变化反应信息,属于一种FSK频移键控。
3.MSK与OQPSK的联系
MSK是一种特殊的OQPSK;先补充OQPSK的相关知识
QPSK和OQPSK 正交相移键控:
Quadriphase-Shift-Keying(QPSK) 是多进制相移键控 M-ary phase-shift-keying (M-PSK) 当M=4时的一种特殊情况,此时 T s = T b l o g 2 M = 2 T b T_s=T_blog_2M=2T_b Ts=Tblog2M=2Tb,相位取值集合 { β i } = { π 4 3 π 4 5 π 4 7 π 4 } \{\beta_i\}=\{\frac{\pi}{4}\frac{3\pi}{4}\frac{5\pi}{4}\frac{7\pi}{4}\} {βi}={4π43π45π47π},其实数域上的数学表达式为: s ( t ) = P m I ( t ) c o s ( 2 π f c t + θ c ) − P m Q ( t ) s i n ( 2 π f c t + θ c ) , s(t)=\sqrt{P}m_I(t)cos(2\pi f_c t +\theta_c)-\sqrt{P}m_Q(t)sin(2\pi f_c t +\theta_c), s(t)=PmI(t)cos(2πfct+θc)−PmQ(t)sin(2πfct+θc), m I ( t ) = ∑ n = − ∞ ∞ a I n p ( t − n T s ) , m Q ( t ) = ∑ n = − ∞ ∞ a Q n p ( t − n T s ) ( 9 ) m_I(t)=\sum_{n=-\infty}^\infty a_{In}p(t-nT_s),m_Q(t)=\sum_{n=-\infty}^\infty a_{Qn}p(t-nT_s) \qquad (9) mI(t)=n=−∞∑∞aInp(t−nTs),mQ(t)=n=−∞∑∞aQnp(t−nTs)(9)显然,当 a I n 和 a Q n a_{In}和a_{Qn} aIn和aQn同时改变时,相位可能发生180°的跳变,这种幅度上大范围的波动是我们所不希望看到的,因此,我们将同相分量和正交分量错开 T s 2 s \frac{T_s}{2}s 2Tss的时间,得到带偏移量的正交相移键控 Offset (Staggered) Quadriphase-Shift-Keying ,这样一来, a I n 和 a Q n a_{In}和a_{Qn} aIn和aQn不会同时发生改变,将相位波动缩小到了90°以内,包络跳动更小,频谱旁瓣也更小(the smaller the flfluctuation, the smaller the sidelobe regeneration and vice versa)。其实数域上的数学模型为: s ( t ) = P m I ( t ) c o s ( 2 π f c t + θ c ) − P m Q ( t ) s i n ( 2 π f c t + θ c ) , s(t)=\sqrt{P}m_I(t)cos(2\pi f_c t +\theta_c)-\sqrt{P}m_Q(t)sin(2\pi f_c t +\theta_c), s(t)=PmI(t)cos(2πfct+θc)−PmQ(t)sin(2πfct+θc), m I ( t ) = ∑ n = − ∞ ∞ a I n p ( t − n T s ) , m Q ( t ) = ∑ n = − ∞ ∞ a Q n p ( t − ( n + 1 2 ) T s ) ( 10 ) m_I(t)=\sum_{n=-\infty}^\infty a_{In}p(t-nT_s),m_Q(t)=\sum_{n=-\infty}^\infty a_{Qn}p(t-(n+\frac12)T_s) \qquad (10) mI(t)=n=−∞∑∞aInp(t−nTs),mQ(t)=n=−∞∑∞aQnp(t−(n+21)Ts)(10) 而对于多进制相移键控来说存在相位模糊的问题(M-fold phase ambiguity),为了解决这个问题引入差分编码(differential encoding);以上都是为了更好的理解从正交看MSK与OQPSK的联系所作的铺垫,不继续深入讨论。
下面讨论MSK与OQPSK的联系:
由(18)可知:由于C(t)和S(t)是彼此Tb的偏移,则由(18)式表示的SMSK(t)可能是半正弦脉冲成型的OQPSK形式。为了证实这一点,进一步讨论实际的I-Q数据序列{
a
n
a_n
an}、{
b
n
b_n
bn}和输入序列{
α
i
\alpha_i
αi}之间的关系以及改变规律。由于每个比特时间内
α
i
\alpha_i
αi都可能变化,
a
n
a_n
an和
b
n
b_n
bn也同样可能在每个比特时间里变化。然而由于式(14)相位连续性的约束,实际上
a
n
a_n
an仅在C(t)的过零点改变,
b
n
b_n
bn仅在S(t)的过零点改变。又C(t)和S(t)的过零点各自是间隔2Tb的,因此an和bn在每2Tb时间处是连续的(不发生跳变,如下图):

进一步由于C(t)和S(t)的波形以2Tb为周期,可以用在I和Q通道的合成的正的有时限脉冲来把这个符号变化和I-Q序列本身相结合。特别地,定义脉冲波形为:
p
(
t
)
=
{
s
i
n
π
t
2
T
b
,
0
≤
t
≤
2
T
b
0
,
o
t
h
e
r
w
i
s
e
(
22
)
p(t) =\begin{cases}sin\frac{\pi t}{2T_b}, & 0\leq t \leq 2T_b \\0, & otherwise\end{cases} \qquad(22)
p(t)={sin2Tbπt,0,0≤t≤2Tbotherwise(22)
这里需要注意到
s
i
n
π
t
2
T
b
sin\frac{\pi t}{2T_b}
sin2Tbπt的周期为4Tb,因此在
0
≤
t
≤
2
T
b
0\leq t \leq 2T_b
0≤t≤2Tb时,p(t)恒为正,则MSK的I-Q表达可以表示为:
s
M
S
K
(
t
)
=
2
E
b
T
b
(
d
c
(
t
)
c
o
s
2
π
f
c
t
−
d
s
(
t
)
s
i
n
2
π
f
c
t
)
,
n
T
b
≤
t
≤
(
n
+
1
)
T
b
(
23
)
s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}(d_c(t)cos2\pi f_ct-d_s(t)sin2\pi f_ct),\quad nT_b\leq t \leq (n+1)T_b \qquad(23)
sMSK(t)=Tb2Eb(dc(t)cos2πfct−ds(t)sin2πfct),nTb≤t≤(n+1)Tb(23)
其中,
d
c
(
t
)
=
∑
n
c
n
p
(
t
−
(
2
n
−
1
)
T
b
)
d
s
(
t
)
=
∑
n
d
n
p
(
t
−
2
n
T
b
)
(
23
)
d_c(t)=\sum_n c_np(t-(2n-1)T_b)\\ d_s(t)=\sum_n d_np(t-2nT_b)\\ \qquad(23)
dc(t)=n∑cnp(t−(2n−1)Tb)ds(t)=n∑dnp(t−2nTb)(23)而
c
n
=
(
−
1
)
n
a
2
n
−
1
d
n
=
(
−
1
)
n
b
2
n
(
24
)
c_n=(-1)^na_{2n-1}\\d_n=(-1)^nb_{2n}\\ \qquad(24)
cn=(−1)na2n−1dn=(−1)nb2n(24)
为完成MSK和正弦脉冲成形OQPSK的类比,需要理解从输入序列{αn}获得(24)需要的I-Q序列的特征,即{a2n-1}和{b2n}是{αn}的差分编码{Vn}序列的奇偶分量。以下图为例:

从图中还可以看出,b2n和a2n-1不会在同一个Tb里发生改变,保证了载波相位不会发生180°的跳变,符合OQPSK的特性。
最终得到MSK的I-Q表示如下图所示。

从图中可以看到MSK的生成类似于OPQSK,只不过脉冲波形是半正弦而不是矩形,另外,以1/Ts作串并变换前对输入序列进行了差分编码。
最后,式(20)的MSK表达式同样可以以差分编码的形式写出:
对奇数n:
s
M
S
K
(
t
)
=
2
E
b
T
b
[
(
v
n
−
1
+
v
n
2
)
c
o
s
[
2
π
(
f
c
+
1
4
T
b
)
]
−
(
v
n
−
1
−
v
n
2
)
c
o
s
[
2
π
(
f
c
−
1
4
T
b
)
]
]
,
n
T
b
≤
t
≤
(
n
+
1
)
T
b
(
25
)
s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}\bigl[(\frac{v_{n-1}+v_n}{2})cos[2\pi(f_c+\frac{1}{4T_b})]-(\frac{v_{n-1}-v_n}{2})cos[2\pi(f_c-\frac{1}{4T_b})]\bigr],\quad nT_b\leq t \leq (n+1)T_b\qquad(25)
sMSK(t)=Tb2Eb[(2vn−1+vn)cos[2π(fc+4Tb1)]−(2vn−1−vn)cos[2π(fc−4Tb1)]],nTb≤t≤(n+1)Tb(25)
对偶数n:
s
M
S
K
(
t
)
=
2
E
b
T
b
[
(
v
n
−
1
+
v
n
2
)
c
o
s
[
2
π
(
f
c
+
1
4
T
b
)
]
+
(
v
n
−
1
−
v
n
2
)
c
o
s
[
2
π
(
f
c
−
1
4
T
b
)
]
]
,
n
T
b
≤
t
≤
(
n
+
1
)
T
b
(
26
)
s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}\bigl[(\frac{v_{n-1}+v_n}{2})cos[2\pi(f_c+\frac{1}{4T_b})]+(\frac{v_{n-1}-v_n}{2})cos[2\pi(f_c-\frac{1}{4T_b})]\bigr],\quad nT_b\leq t \leq (n+1)T_b\qquad(26)
sMSK(t)=Tb2Eb[(2vn−1+vn)cos[2π(fc+4Tb1)]+(2vn−1−vn)cos[2π(fc−4Tb1)]],nTb≤t≤(n+1)Tb(26)
写在一个式子中即:
s
M
S
K
(
t
)
=
2
E
b
T
b
[
(
v
n
−
1
+
v
n
2
)
c
o
s
[
2
π
(
f
c
+
1
4
T
b
)
]
+
(
−
1
)
n
(
v
n
−
1
−
v
n
2
)
c
o
s
[
2
π
(
f
c
−
1
4
T
b
)
]
]
,
n
T
b
≤
t
≤
(
n
+
1
)
T
b
(
27
)
s_{MSK}(t)=\sqrt{\frac{2E_b}{T_b}}\bigl[(\frac{v_{n-1}+v_n}{2})cos[2\pi(f_c+\frac{1}{4T_b})]+(-1)^n(\frac{v_{n-1}-v_n}{2})cos[2\pi(f_c-\frac{1}{4T_b})]\bigr],\quad nT_b\leq t \leq (n+1)T_b\qquad(27)
sMSK(t)=Tb2Eb[(2vn−1+vn)cos[2π(fc+4Tb1)]+(−1)n(2vn−1−vn)cos[2π(fc−4Tb1)]],nTb≤t≤(n+1)Tb(27)
三、MSK的CPM调制和I-Q调制仿真
关于MSK的调制网上有很多Matlab仿真程序,这里附上我的,唯一的优点就是注释非常详细…
MSK的CPM调制
MSK的正交调制程序还没有通过审核,有机会再补上,如若需要可以去我的主页里下载。
下面是部分仿真波形
CPM调制
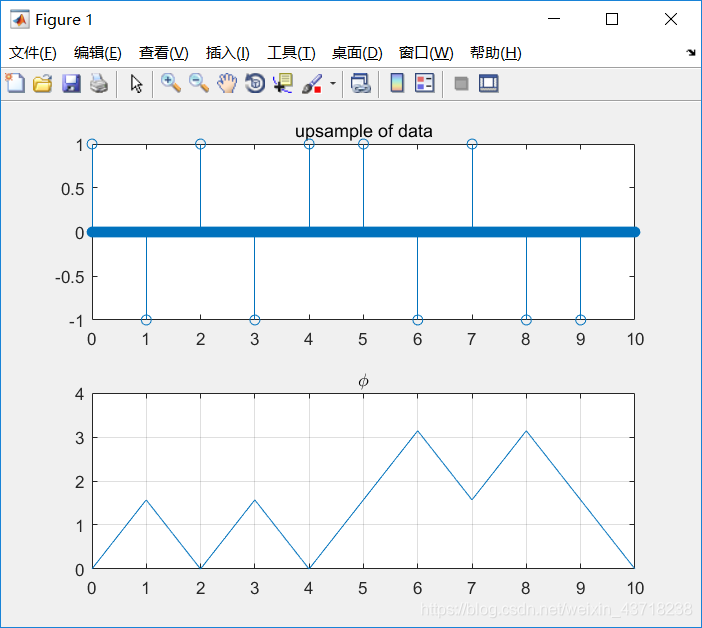

I-Q调制
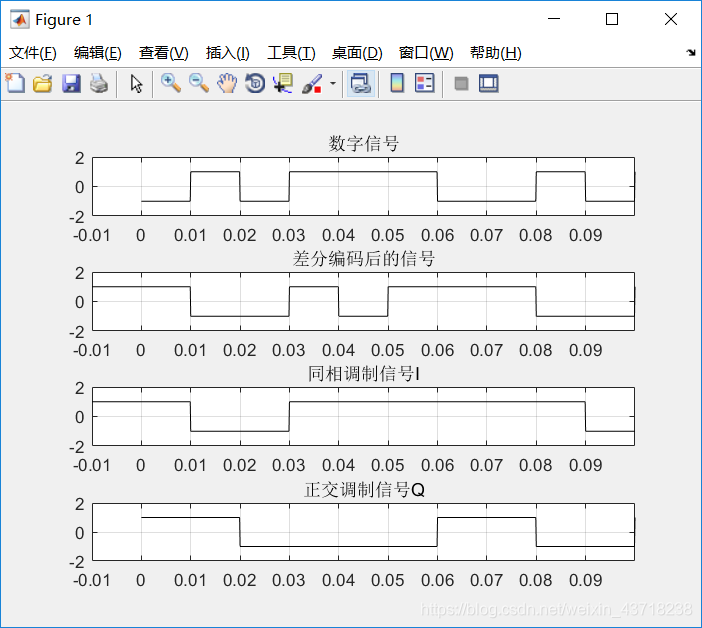








 本文深入探讨最小频移键控(MSK)的连续相位调制(CPM)及正交表示,解析MSK的数学模型,揭示其与FSK、OQPSK的关系,并提供详细的MSK调制仿真代码。
本文深入探讨最小频移键控(MSK)的连续相位调制(CPM)及正交表示,解析MSK的数学模型,揭示其与FSK、OQPSK的关系,并提供详细的MSK调制仿真代码。
















 4874
4874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








