数学基础&&信息论
提示:一些常忘或容易混淆的数学基础概念及公式,以便日后自己查看
一、数学基础
1、复数
任何复数都可以表示为:
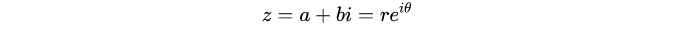
a和b是实数,而i是虚数单位,它有着性质
i
2
=
−
1
i^2=-1
i2=−1。实数a叫做复数的实部,而实数b叫做复数的虚部。
复平面:横的叫实轴,竖的叫虚轴,然后确定0的位置,
z
=
a
+
b
i
z=a+bi
z=a+bi可以用二维空间来表示出来。
共轭复数是z关于实数轴的“对称点”:
z
=
a
−
i
b
z=a-ib
z=a−ib
绝对值(模):
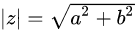
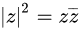
数域的具体解说可见文章欧拉公式,复数域的成人礼
2、多项式
P
n
(
t
)
=
a
0
+
a
1
∗
t
+
a
2
∗
t
2
+
.
.
.
+
a
n
∗
t
n
Pn(t) = a0 + a1*t + a2*t^2 + ... +an*t^n
Pn(t)=a0+a1∗t+a2∗t2+...+an∗tn
Pn(t)的一组基为
[
1
,
t
,
t
2
,
.
.
.
,
t
n
]
[1, t, t^2, ... ,t^n]
[1,t,t2,...,tn]
多项式相乘公式
1、完全平方
(
a
+
b
)
2
=
a
(
a
+
b
)
+
b
(
a
+
b
)
=
a
2
+
2
a
b
+
b
2
(a+b)^2=a(a+b)+b(a+b)=a^2+2ab+b^2
(a+b)2=a(a+b)+b(a+b)=a2+2ab+b2
(
a
−
b
)
2
=
a
(
a
−
b
)
−
b
(
a
−
b
)
=
a
2
−
2
a
b
+
b
2
(a-b)^2=a(a-b)-b(a-b)=a^2-2ab+b^2
(a−b)2=a(a−b)−b(a−b)=a2−2ab+b2
2、平方差
(
a
+
b
)
(
a
−
b
)
=
a
(
a
−
b
)
+
b
(
a
−
b
)
=
a
2
−
b
2
(a+b)(a-b)=a(a-b)+b(a-b)=a^2-b^2
(a+b)(a−b)=a(a−b)+b(a−b)=a2−b2
3、完全立方
(
a
+
b
)
3
=
(
a
2
+
2
a
b
+
b
2
)
(
a
+
b
)
=
a
3
+
3
a
2
b
+
3
a
b
2
+
b
3
(a+b)^3=(a^2+2ab+b^2)(a+b)=a^3+3a^2b+3ab^2+b^3
(a+b)3=(a2+2ab+b2)(a+b)=a3+3a2b+3ab2+b3
(
a
−
b
)
3
=
(
a
2
−
2
a
b
+
b
2
)
(
a
−
b
)
=
a
3
−
3
a
2
b
−
3
a
b
2
+
b
3
(a-b)^3=(a^2-2ab+b^2)(a-b)=a^3-3a^2b-3ab^2+b^3
(a−b)3=(a2−2ab+b2)(a−b)=a3−3a2b−3ab2+b3
4、立方和差
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
=
(
a
3
−
a
2
b
+
a
b
2
)
+
(
a
2
b
−
a
b
2
+
b
3
)
=
a
3
+
b
3
(a+b)(a^2-ab+b^2)=(a^3-a^2b+ab^2)+(a^2b-ab^2+b^3)=a^3+b^3
(a+b)(a2−ab+b2)=(a3−a2b+ab2)+(a2b−ab2+b3)=a3+b3
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
=
(
a
3
+
a
2
b
+
a
b
2
)
−
(
a
2
b
+
a
b
2
+
b
3
)
=
a
3
−
b
3
(a-b)(a^2+ab+b^2)=(a^3+a^2b+ab^2)-(a^2b+ab^2+b^3)=a^3-b^3
(a−b)(a2+ab+b2)=(a3+a2b+ab2)−(a2b+ab2+b3)=a3−b3
3、函数
Gamma 函数

gamma函数具体解释及推导过程见文章LDA-math - 神奇的 Gamma 函数
克罗内克(Kronecker)函数
又称克罗内克δ函数、克罗内克δ、克罗内克符号,得名于德国数学家 利奥波德·克罗内克 。克罗内克函数δ(x, y)是一个 二元函数 ,自变量 (输入值)一般是两个整数 ,如果两者相等,则其输出值为1,否则为0,即当 x= y 时, δ(x, y)=1, 否则δ(x, y) = 0 。
4、排列与组合
组合数
组合数的两种表达形式:
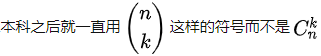
原因参考知乎回答-组合数记法
求解方法常见公式为
其他求解方法见计算组合数的几种方法总结
5、线性变换

具体解释见知乎问题-如何理解几何重数和代数重数?
6、正交矩阵
正交矩阵(Orthogonal Matrix)是指其转置等于其逆的矩阵。
当
A
A
T
=
A
A
−
1
AA^T = AA^{-1}
AAT=AA−1,即
A
T
=
A
−
1
A^T = A^{-1}
AT=A−1时,A是正交矩阵。
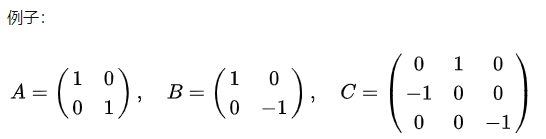
因为
A
A
T
=
I
AA^T = I
AAT=I,也就是说矩阵的行(或列)向量之间点积等于0(向量正交),行(或列)向量与自身的点积等于1(单位向量),所以正交矩阵又有另一种定义:由行之间两两正交、列之间两两正交的单位向量组成的方阵。
此外,正交矩阵的行列式必定是+1或-1。
7、概率统计
1、伯努利分布 X ~ Bernoulli ( p )
扔一次硬币,随机变量X可取为“正面朝上”
2、二项分布 X ~ Binomial (n, p)
扔n次硬币,随机变量X可取为“正面(反面)朝上为Xi”,n次后共有m次正面朝上
3、贝塔分布 p ~ Beta (a,b)
随机变量p即为二项分布中的概率(参数)p
4、category分布 X ~ Category (p1,p2,…,pk)或X ~ Multinomial (p1,p2,…,pk)
扔一次骰子,随机变量X可取为“正面朝上的点数为某一常量i”,此时k最大取6
对于category分布有时会通过dummy variable Xi来增强理解
5、多项分布 X ~ Multinomial (n, p1,p2,…,pk)
扔n次骰子,随机变量X可取为“某点数朝上为Xi”,n次后共有xi次某点数朝上
6、Dirichlet分布 P ~ Dirichlet (α1,α2,…,αk)
随机变量P即为多项分布中的p1,p2,…,pk
概率统计13——二项分布与多项分布
二、信息论基础
1、熵(Entropy)
定义随机变量x在概率分布p的熵:
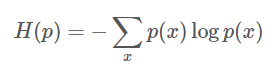
相对熵(Relative Entropy),也称KL散度 (Kullback–Leibler divergence)。
p(x),q(x)为随机变量x的两个概率分布,定义p对q的相对熵(KL散度)为:
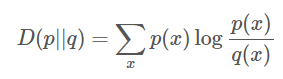
KL散度在p(x)和q(x)相同时取到最小值0,两个概率分布越相似,则KL散度越小。
注意, D ( p ∣ ∣ q ) ! = D ( q ∣ ∣ p ) D(p||q) != D(q||p) D(p∣∣q)!=D(q∣∣p),也不满足三角不等式。
假设p(x)是随机变量的真实分布,q(x)是模型预测的分布,则可以用KL散度作为分类问题的Loss Function,通过训练使预测分布接近于真实分布。
交叉熵(Cross Entropy):

在分类问题中,随机变量的真实分布p(x)是确定的,于是H§也是确定的,相当于一个常数。因此,优化KL散度与优化交叉熵等价,这也是为什么用交叉熵作为分类问题损失函数的原因。
以上引自熵,交叉熵,KL散度公式与计算实例





















 5061
5061











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








