训练神经网络—激活函数的选择
文章目录
神经元的输入在线性求和之后需要使用非线性的激活函数来把它激活，正是因为非线性的激活函数才能为神经网络带来非线性，才可以拟合非线性的决策边界以解决非线性的分类和回归问题。
我们可以将激活函数分为两类：分别是“饱和激活函数”以及“非饱和激活函数”。
1、Sigmoid函数
Sigmoid函数表达式
σ ( x ) = 1 1 + e − x \sigma \left( x \right) =\frac{1}{1+e^{-x}} σ(x)=1+e−x1 {$$}
Sigmoid函数图像
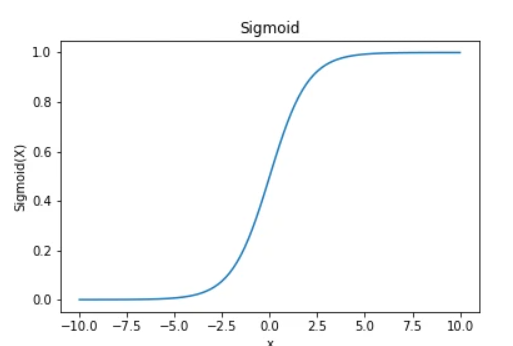
Sigmoid函数特点
- 该函数是挤压函数，可以把数值挤压在[0,1]之间。
- 该函数可解释性好，可类比神经细胞是否激活，本质上可以划分为二分类问题，0为一类，1为一类。
Sigmoid函数缺点
在实际编程中，我们几乎不选择Sigmoid函数作为激活函数，主要是因为Sigmoid函数存在三个问题：
①饱和性会导致梯度消失现象（x过大或过小的时候接近于0）
举例说明：
L
=
[
σ
(
w
x
+
b
)
2
]
,
σ
(
x
)
=
1
1
+
e
−
x
∂
L
∂
x
=
∂
L
∂
σ
⋅
∂
σ
∂
x
=
2
⋅
σ
(
w
x
+
b
)
⋅
σ
′
(
x
)
=
2
⋅
σ
(
w
x
+
b
)
⋅
σ
(
w
x
+
b
)
(
1
−
σ
(
w
x
+
b
)
)
⋅
w
L\,\,=\,\,\left[ \sigma \left( wx+b \right) ^2 \right] ,\sigma \left( x \right) =\frac{1}{1+e^{-x}} \\ \frac{\partial L}{\partial x}=\frac{\partial L}{\partial \sigma}\cdot \frac{\partial \sigma}{\partial x} \\ \,\, =2\cdot \sigma \left( wx+b \right) \cdot \sigma '\left( x \right) \\ \,\, =2\cdot \sigma \left( wx+b \right) \cdot \sigma \left( wx+b \right) \left( 1-\sigma \left( wx+b \right) \right) \cdot w
L=[σ(wx+b)2],σ(x)=1+e−x1∂x∂L=∂σ∂L⋅∂x∂σ=2⋅σ(wx+b)⋅σ′(x)=2⋅σ(wx+b)⋅σ(wx+b)(1−σ(wx+b))⋅w
当x=-10时，局部梯度趋近于0
当x= 0 时，局部梯度等于0.25
当x = 10时，局部梯度等于0
②经过激活函数后，输出值不再关于零对称，且伴随ZigZagPath现象。
每个神经元中函数关于权重值的导数同号，即所有的权重值要么一起增大要么一起减小，同步增长。
举例说明：
假如有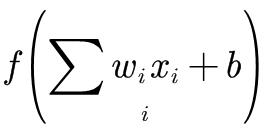
，即有
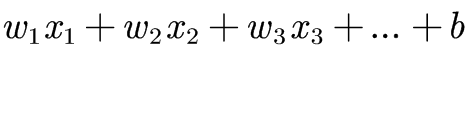用f=sigmoid函数激活，对
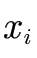求偏导有
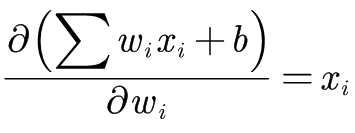，其中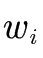
为本层输入（同时也可以看做上一层的输出)，若上层神经元全用sigmoid激活，那么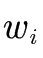一定为正数，即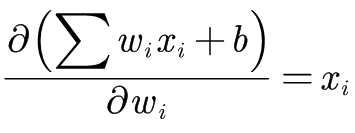的结果都是整数，即所有权重要么同时增大，要么同时减小，即会出现zigzagpath现象。
③exp()指数运算相较于其他运算会更加消耗计算资源。
2、双曲正切函数
双曲正切函数表达式
tanh x = e x − e − x e x + e − x \tanh x=\frac{e^x-e^{-x}}{e^x+e^{-x}} tanhx=ex+e−xex−e−x
双曲正切函数图像
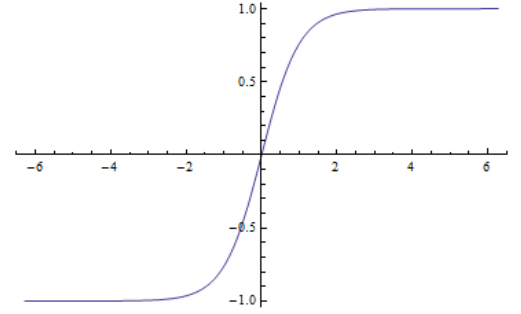
双曲正切函数特点
从双曲正切函数的图像和sigmoid函数类似，两者之间可以通过缩放，平移变换得到，相比于sigmoid函数的优点就是函数的输出值有正有负，解决了zigzagpath现象。
双曲正切函数缺点
①饱和现象
双曲正切函数同样在输入值过大或过小时产生饱和现象，即会出现梯度消失现象。
3、Relu函数及其变形
Relu函数表达式
σ ( x ) = { x i f x ⩾ 0 0 o t h e r w i s e \sigma \left( x \right) =\begin{cases} x\,\,\,\,if\,\,x\geqslant 0\\ 0\,\,\,\,otherwise\\ \end{cases} σ(x)={xifx⩾00otherwise
Relu函数图像
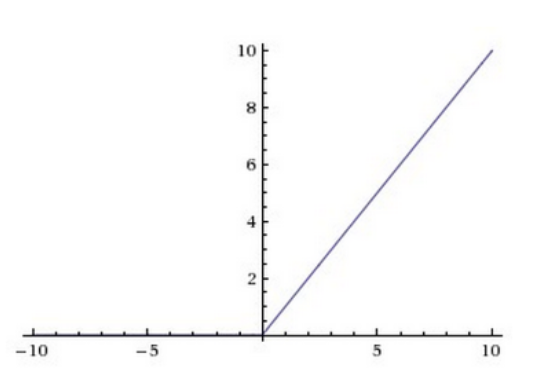
Relu函数特点
由图像可以看出来在x小于0的部分，函数的取值都为0，也就是把输入值x小于0的部分都抹平了，这也叫做整流（Relu函数叫做线性整流函数，又称修正线性单元）。该函数从图像上可以看出：随着x的增大，输出值也增大，不会发生饱和。由于在x大于0的部分，函数对数据没有经过处理，直接输出，所以relu函数易于计算，消耗的计算资源少（在CIFAR-10数据集上，使用不同的激活函数来训练4层的CNN网络收敛速度不同，relu要比sigmoid和tanh快6倍以上）
Relu函数缺点
①输出不关于0对称
从图像可以看出，当x小于0时，图像输出为0，即函数的梯度也是0，代表神经元死亡或瘫痪。（Dead Relu will never activate which means never update）
产生原因
1.初始化不良：随机初始化权重可能会导致产生大部分输入都是0甚至全部都是0的现象，即梯度也是0。2.学习率太大，会跳入黑洞。
改进优化
增添偏置项
开始时Relu函数增加一个偏置项0.01即可保证不会出现输出值为0的情况：
σ
(
x
)
=
max
(
0
,
x
)
+
0.01
\sigma \left( x \right) =\max \left( 0,x \right) +0.01
σ(x)=max(0,x)+0.01
Leaky Relu
函数表达式：
σ
(
x
)
=
{
x
i
f
x
⩾
0
α
x
o
t
h
e
r
w
i
s
e
\sigma \left( x \right) =\begin{cases} x\,\,\,\,if\,\,x\geqslant 0\\ \alpha x\,\,\,\,otherwise\\ \end{cases}
σ(x)={xifx⩾0αxotherwise
函数图像：
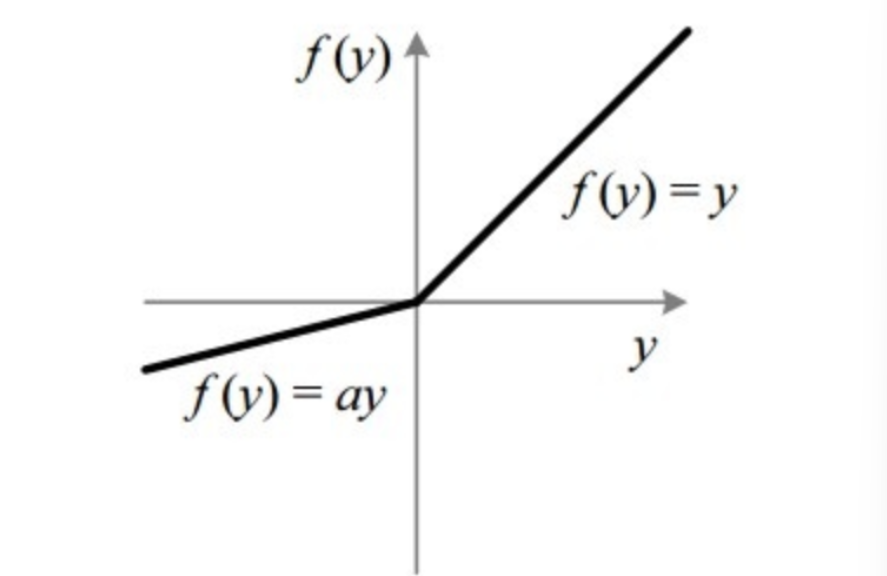
函数特点：
在Leaky Relu中，参数是提前人为指定的，通常为0.01，函数在所有取值上都不会饱和，同时解决了relu函数中当x小于0时出现梯度为0的情况。
PRelu
函数表达式：
σ
(
x
)
=
{
x
i
f
x
⩾
0
α
x
o
t
h
e
r
w
i
s
e
\sigma \left( x \right) =\begin{cases} x\,\,\,\,if\,\,x\geqslant 0\\ \alpha x\,\,\,\,otherwise\\ \end{cases}
σ(x)={xifx⩾0αxotherwise
函数图像：
函数特点：
参数化修正线性单元（Parametic Rectifier），在PRelu中，参数是反向传播过程中根据数据值大小，由神经网络自己学习的，而非预先定义，通常为0.01，函数在所有取值上都不会饱和，同时解决了relu函数中当x小于0时出现梯度为0的情况。
RRelu
函数表达式：
σ
(
x
)
=
{
x
i
f
x
⩾
0
α
x
o
t
h
e
r
w
i
s
e
\sigma \left( x \right) =\begin{cases} x\,\,\,\,if\,\,x\geqslant 0\\ \alpha x\,\,\,\,otherwise\\ \end{cases}
σ(x)={xifx⩾0αxotherwise
函数图像：
函数特点：
随机修正线性单元（ randomized leaky rectified），在RRelu中，参数在训练集中是随机的，即在某个区间内变动，在之后的测试中就变成了固定的值，不再改变。
ERelu
函数表达式：
σ
(
x
)
=
{
x
i
f
x
⩾
0
α
(
e
x
−
1
)
o
t
h
e
r
w
i
s
e
\sigma \left( x \right) =\begin{cases} x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,x\geqslant 0\\ \alpha \left( e^x-1 \right) \,\,\,\,\,otherwise\\ \end{cases}
σ(x)={xifx⩾0α(ex−1)otherwise
函数图像：
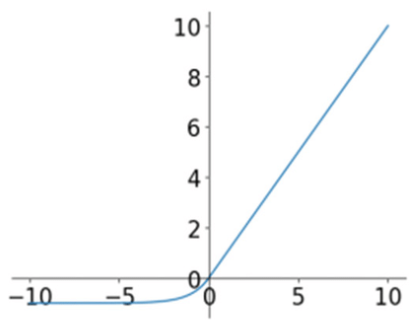
函数特点：
随机修正线性单元（ randomized leaky rectified），在RRelu中，参数在训练集中是随机的，即在某个区间内变动，在之后的测试中就变成了固定的值，不再改变。
4、Maxout
参考：Maxout
Maxout表达式
h i ( x ) = max j ∈ [ 1 , k ] z i j z i j = x T W . . . i j + b i j h_i\left( x \right) \,\,=\,\,\underset{j\in \left[ 1,k \right]}{\max}z_{ij} \\ z_{ij}\,\,=\,\,x^TW_{...ij}\,\,+\,\,b_{ij} hi(x)=j∈[1,k]maxzijzij=xTW...ij+bij
Maxout函数示意图（k=2）
before:
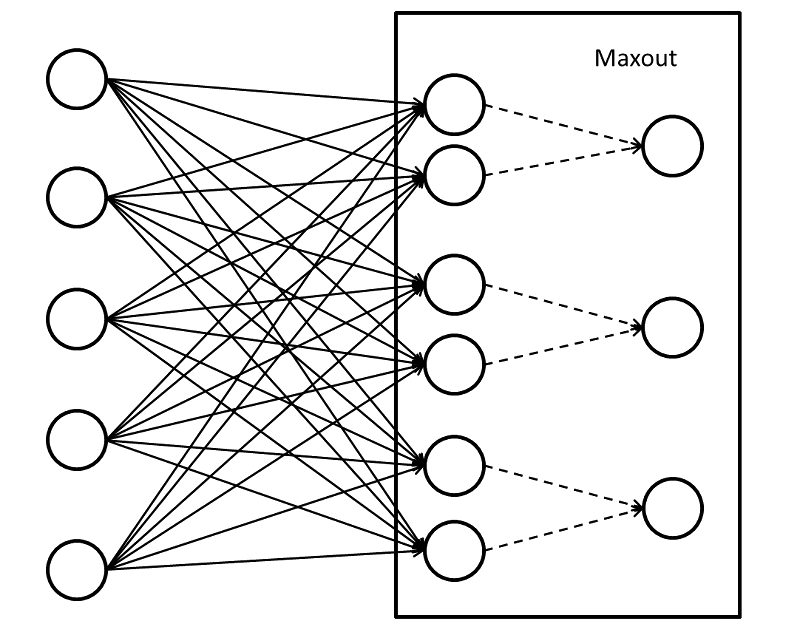
该图是基本的Maxout连接示意图，前半部分与常见的全连接层并无区别，之后每两个单元"连接"到一个单元上（由于五参数，故并非真正连接），从这两个单元中如何选出一个单元值呢，那也就是比较这两个单元中的最大值，大的值便可通过，这也就是maxout。
after：
两个单元中最大的单元被选出。
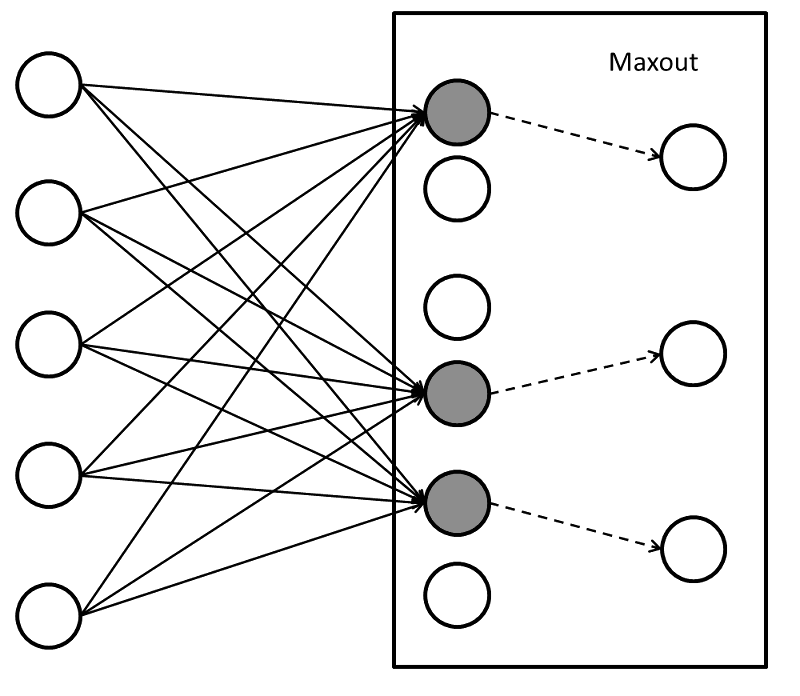
Maxout函数特点
Maxout不仅仅是激活函数，还改变了神经网络的结构。我们知道在该层神经网络中，每个单元都是上层特征的线性组合，那么如果一个单元学到了y=0，另一个学到了y=x，那么本质上相当于Relu激活函数。
如果我们使每个k单元都连接到一个单元上，那么Maxout可以学习到更多段的分段函数作为激活函数，当k足够大时，理论上可以拟合任何凸函数。
总结
- Use Relu.Be careful with your learning rates.(要使用Relu，但是我们要注意学习率不要太大，否则可能会跳入黑洞)
- Try out tanh but donnot except much.(可以使用双曲正切函数，但是不要对结果抱有太大希望)
都连接到一个单元上，那么Maxout可以学习到更多段的分段函数作为激活函数，当k足够大时，理论上可以拟合任何凸函数。
总结
- Use Relu.Be careful with your learning rates.(要使用Relu，但是我们要注意学习率不要太大，否则可能会跳入黑洞)
- Try out tanh but donnot except much.(可以使用双曲正切函数，但是不要对结果抱有太大希望)
- Donnot use sigmoid(不要在中间层轻易使用sigmoid)
365
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
