文章目录
呃呃,在看learnopengl的立方体贴图那张,做环境映射的时候,需要用到世界空间中的法线信息,但是很离谱,我又忘了,这里直接转载一下别的大佬的文章,作为自己的记录,下次忘了就直接翻自己的博客,文章末尾放了引用的文章链接。
0. 背景介绍
很多 顶点着色器 ( vertex shader) 中都用到法线矩阵 ( normal matrix )。本文内容涉及法线矩阵是什么、法线矩阵有什么用。
有很多计算工作是在 观测空间 ( eye space ) 下完成的,其中包括与光照相关的计算。如果不在观测空间计算,与观测位置相关的效果将很难实现,如高光 ( specular )。
因此,我们需要一种方法,将法线转换到观测空间。将顶点变换到观测空间的计算,可以写成:
vertexEyeSpace = gl_ModelViewMatrix * gl_Vertex;
那为什么不能对法线做一遍同样的操作呢?法线是有 3 个浮点数分量的向量,模型-观测矩阵 是 4x4 的矩阵。法线是一个向量,我们只想改变其方向。模型-观测矩阵 左上区域的 3x3 矩阵包含改变方向的子矩阵,那我们为什么不直接用法向量左乘这个子矩阵?
1.错误的做法与分析
这很容易通过下面的代码实现:
normalEyeSpace = vec3(gl_ModelViewMatrix * vec4(gl_Normal, 0.0f));
所以,gl_NormalMatrix 只是一个简化或优化代码编写的捷径?不,不是的。上面一行代码只在某些情况下有效。
让我们看看潜在的问题:
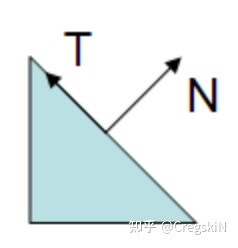
上图中有一个三角形、一条法向量、一条切向量。下图将展示当 模型-观测矩阵 包含非均匀的缩放时,会发生什么。
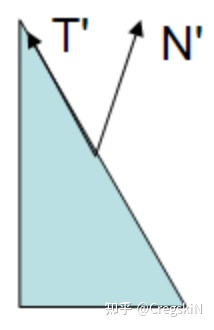
注意:如果缩放是均匀的,法线的方向将保持不变,长度会受影响,但很容易通过单位化修复
如果上图的 模型-观测矩阵 被应用到所有顶点和法线,显然会得到错误的结果:法线将不再垂直于平面。
我们知道,向量可以用两个点的差表示。比如切向量,可以通过三角形边上的两个顶点做差得到。如果
P
1
P_1
P1 和
P
2
P_2
P2 就是定义在三角形边上的两个顶点,可以得到:
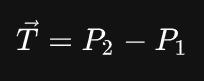
考虑到在齐次坐标中,向量可以用含四个分量的元组表示 ( 最后一个分量为 0 ),可以让等号两侧同时左乘 模型-观测矩阵:

化简成:

因为
P
1
′
P'_1
P1′ 和
P
2
′
P'_2
P2′ 是变换后三角形边上的顶点,所以
T
′
T'
T′ 仍然是三角形边上的切向量,故可以认为:模型-变换矩阵 保留了切向量,却没有保留法向量。
2. 改进与推导
考虑对向量
T
′
⃗
\vec{T'}
T′ 采用的方法,我们可以假设两个顶点,如下:
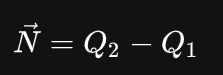
主要的问题如之前图中展示的那样,通过变换后的点定义的向量
Q
2
′
Q'_2
Q2′-
Q
1
′
Q'_1
Q1′ 不一定保持原样 ( 原来是垂直于三角形面的 )。法向量不像切向量那样,通过两个点做差定义,而只定义为一个垂直于平面的向量。
所以,我们明白了,不能简单地把 模型-观测矩阵 应用于所有情况下的法向量。那问题来了,我们应该用啥样的矩阵呢?
考虑一个 3x3 的矩阵 G ,然后我们来看看这个矩阵如何计算,并完美地转换法向量。
在变换前后,
T
⃗
\vec{T}
T 和
N
⃗
\vec{N}
N 都是垂直的,因此在变换前,满足
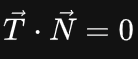
变换后还满足
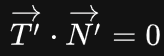
切向量 T ⃗ \vec{T} T 可以安全地左乘 模型-观测矩阵 左上方的 3x3 子矩阵 ( T ⃗ \vec{T} T 是一个齐次坐标下的向量,w 分量为 0 ),我们把这个子矩阵称为 M M M
假设矩阵 G 能正确的转换法向量
N
⃗
\vec{N}
N ,得出等式:
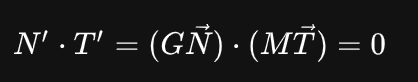
向量点积等价于对应分量乘积之和,得:
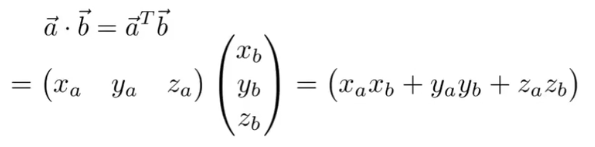
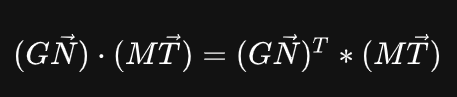
注意:第一个向量必须转置,以便计算对应分量乘积之和
我们还知道,乘法的转置,就是转置的乘法,即:

所以:
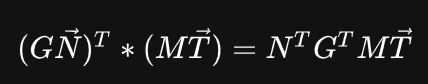
首先声明
N
⃗
\vec{N}
N ·
T
⃗
\vec{T}
T = 0 ,所以如果有:
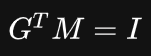
那就能满足我们的声明:
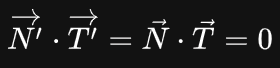
所以通过 M 反推出 G :

3. 总结
因此,能正确转换法向量的矩阵,就是 M M M 的逆的转置。OpenGL 在 gl_NormalMatrix 中进行这步计算。
在本节开始提到,在某些情况下,模型-变换矩阵 可以直接应用于法向量的变换,即当 模型-观测矩阵 是正交矩阵时:
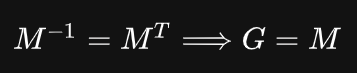
对于正交矩阵,其转置等于其逆。那什么是正交矩阵呢?
- 一个正交矩阵,任意的行/列都是单位长度,且互相垂直。
- 两个向量分别乘正交矩阵后的夹角,与变换前是一致的。
- 简单地说,变换保留了向量之间的角度关系,因此变换后的法线与切线仍互相垂直!此外,还保留了向量的长度。
那如何确定 M 是正交矩阵呢?
- 当我们的变换中,只包含旋转和平移,即在 OpenGL 中,我们只使用 glRotate 和 glTranslate,而不使用 glScale。这样操作能保证 M 是正交的。注意: gluLookAt 也创建了一个正交矩阵!
4. 例子GLSL:用transpose和inverse函数转换顶点着色器里的法线向量
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
out vec3 FragPos;
out vec3 Normal;
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;
void main()
{
FragPos = vec3(model * vec4(aPos, 1.0));
Normal = mat3(transpose(inverse(model) ) ) * aNormal;
gl_Position = projection * view * vec4(FragPos, 1.0);
}
为什么要转换顶点着色器里的法线向量?
- 为了确定法线向量在顶点着色器里的方向始终垂直于表面。
- 如果模型矩阵进行非一致性(non-uniform)缩放(scale),顶点变化后,其法线向量不再垂直于表面,所以需要法线矩阵
- 法线矩阵是 乘 法线向量,可把该法线转化为即使缩放也不会不垂直于表面的法线向量
- 法线矩阵可从模型视图矩阵转换而来(转置逆转矩阵),但因为是工作在世界空间(而不是视图空间),所以用模型矩阵转换
- 把模型矩阵转化为3x3矩阵(用mat3)失去转置属性,而后可和vec3向量相乘
新增:TBN空间和TBN矩阵
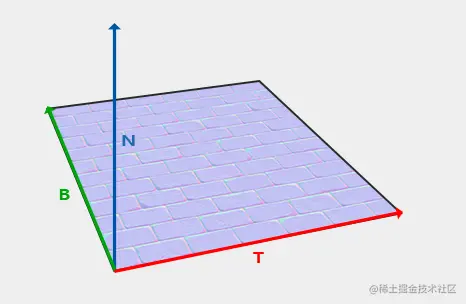
- 切线空间定义于每一个顶点之中,是由切线( T a n g e n t Tangent Tangent),副切线( B i T a n g e n t BiTangent BiTangent),顶点法线( N o r m a l Normal Normal)以模型顶点为中心的坐标空间。
- n o r m a l M a p normalMap normalMap 中的法向量在切空间中表示,其中法向量总是大致指向正z方向。
- 切线空间是一个三角形表面的局部空间:法线相对于单个三角形的局部参考系。把它想象成法向量的局部空间;它们都是指向正z方向的不管最终变换的方向是什么。
- 使用一个特定的矩阵,我们可以将这个局部切线空间的法向量转换为世界或视图坐标,并将它们沿最终映射曲面的方向定向。这个矩阵就是
T
B
N
TBN
TBN 矩阵。接下来将详细推导
T
B
N
TBN
TBN 矩阵的构造过程。
 只需要下面两个步骤即可得到规范化的
T
B
N
TBN
TBN 矩阵:
只需要下面两个步骤即可得到规范化的
T
B
N
TBN
TBN 矩阵:
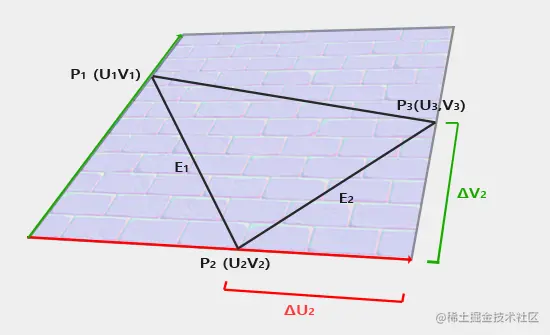
E 1 = Δ U 1 T + Δ V 1 B E 2 = Δ U 2 T + Δ V 2 B E_1 = \Delta U_1T + \Delta V_1B \\ E_2 = \Delta U_2T + \Delta V_2B E1=ΔU1T+ΔV1BE2=ΔU2T+ΔV2B
该公式的数学意义是,如何将一个点从uv空间映射到三维空间,其中TB作为基矢量,以uv空间中u和v的增长作为控制参数,假设三角形中存在一点p,则 A P ⃗ = u ( p ) ∗ T ⃗ + v ( p ) ∗ B ⃗ \vec {AP}=u(p) * \vec T + v(p) * \vec B AP=u(p)∗T+v(p)∗B , (点p可以表示为以TB为基矢量的uv空间,TB轴的线性组合,在这里A是UV坐标原点)。
根据以上公式可以快速的推导出TB:
T
⃗
=
Δ
V
1
E
2
−
Δ
V
2
E
1
Δ
V
1
Δ
U
2
−
Δ
V
2
Δ
U
1
B
⃗
=
−
Δ
U
1
E
2
+
Δ
U
2
E
1
Δ
V
1
Δ
U
2
−
Δ
V
2
Δ
U
1
\vec T = \frac {\Delta V_1E_2 - \Delta V_2E_1}{\Delta V_1 \Delta U_2 - \Delta V_2 \Delta U1}\\ \space \\ \vec B = \frac {- \Delta U_1E_2 + \Delta U_2E_1}{\Delta V_1 \Delta U_2 - \Delta V_2 \Delta U1}
T=ΔV1ΔU2−ΔV2ΔU1ΔV1E2−ΔV2E1 B=ΔV1ΔU2−ΔV2ΔU1−ΔU1E2+ΔU2E1
目前给出的TB还是不是真正的切线与副切线,需要正交化后得到
T
B
N
TBN
TBN 矩阵:
t
⊥
⃗
=
n
o
r
m
a
l
i
z
e
d
(
t
⃗
−
(
t
⃗
⋅
n
⃗
)
n
⃗
)
b
⊥
⃗
=
n
o
r
m
a
l
i
z
e
d
(
b
⃗
−
(
b
⃗
⋅
n
⃗
)
n
⃗
−
(
b
⃗
⋅
t
⊥
⃗
)
t
⊥
)
\vec {t_{\perp}} = normalized(\vec t - (\vec t · \vec n)\vec n)\\ \space \\ \vec {b_{\perp}} = normalized(\vec b - (\vec b · \vec n)\vec n - (\vec b · \vec {t_{\perp}}) t_{\perp})\\
t⊥=normalized(t−(t⋅n)n) b⊥=normalized(b−(b⋅n)n−(b⋅t⊥)t⊥)
- t ⃗ \vec t t 是正交前的切线方向,也可以说是u方向。
- b ⃗ \vec b b 是正交前的副切线方向,也可以说是v方向。
- 而 t ⊥ ⃗ \vec {t_{\perp}} t⊥ 和 b ⊥ ⃗ \vec {b_{\perp}} b⊥ 表示的是正交后的切线方向和正交后的副切线方向。正交后的切线和副切线才能算作是切向空间的坐标轴。
- 切向空间是由切线 t ⊥ ⃗ \vec {t_{\perp}} t⊥ 、副切线 b ⊥ ⃗ \vec {b_{\perp}} b⊥ 、顶点法线 n ⃗ \vec n n 以模型顶点为中心的坐标空间。也就是说切线空间的三个坐标轴就是( t ⊥ ⃗ \vec {t_{\perp}} t⊥, b ⊥ ⃗ \vec {b_{\perp}} b⊥, n ⃗ \vec n n)。
- (另一种理解:其中n是建模软件中规定的顶点法线,可以看到n在正交化过程中不会受到影响,该过程是对TB向量进行方向的调整以及长度的归一化。TB在此过程后会相互垂直,此时将不再一定与UV方向保持相同。特别的,当调整顶点法线后,TB平面甚至将与三维空间中的三角形平面不同,也就是说归正交化后的 T B N TBN TBN 矩阵, T B TB TB 轴将不再与uv相等,uv是正交化前的 T B TB TB 轴。)
通过正交化后的
T
a
n
g
e
n
t
(
T
)
Tangent(T)
Tangent(T),
B
i
t
a
n
g
e
n
t
(
B
)
Bitangent(B)
Bitangent(B),
N
o
r
m
a
l
(
N
)
Normal(N)
Normal(N) 可以推导出
T
B
N
TBN
TBN 矩阵:
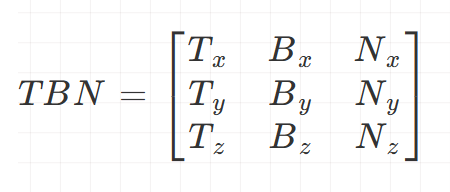
n
o
r
m
a
l
M
a
p
normalMap
normalMap 中存储的法线信息是基于
T
B
N
TBN
TBN 空间的,而光照计算需要所有的参数在同一空间下,以上计算出的
T
B
N
TBN
TBN 矩阵就是用于实现将
T
B
N
TBN
TBN 空间中定义的法线转换到世界空间。
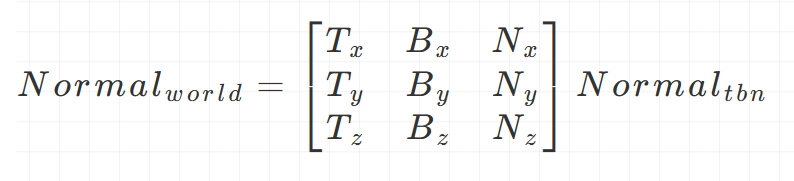
根据矩阵的逆的性质,
T
B
N
TBN
TBN 矩阵的逆矩阵可以用来将矢量从世界空间转换到
T
B
N
TBN
TBN 空间中,而
T
B
N
TBN
TBN 矩阵是正交化过的,根据正交矩阵的特殊性质(正交矩阵的逆等于其转置),可以轻松求得
T
B
N
TBN
TBN 的逆矩阵:
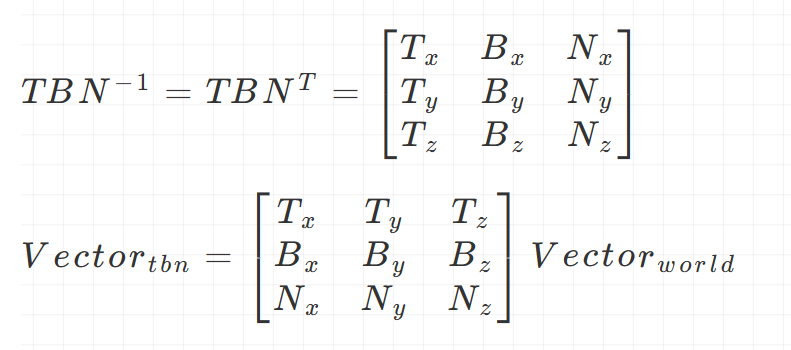
TBN矩阵注意点
这里还有一些需要记住的东西:
- 法线贴图中的法线向量是定义在切线空间中。
- TBN矩阵是切线空间和其他空间的转换矩阵。
- TBN矩阵是正交矩阵,即 ( T B N ) T = = ( T B N ) − 1 (TBN)^T == (TBN)^{-1} (TBN)T==(TBN)−1 ,矩阵的转置=矩阵的逆 。
- Unity的mul函数对矩阵和向量的运算做了不同的处理,以 float3x3矩阵 和 float3向量 为例:
- mul(向量, 矩阵)—— 行向量*矩阵,得行向量。
- mul(矩阵, 向量)——矩阵*列向量,得列向量。
- Unity的TBN矩阵(先行再列)在 mul函数的参数顺序:
- 其他空间 → \rightarrow → 切向空间:TBN矩阵在前,如 lDirTS = mul(TBN_OS, lDirOS);
- 切向空间 → \rightarrow → 其他空间(法线贴图使用):TBN矩阵在后,如 nDirWS = mul(nDirTS, TBN_WS)。
- UnityShader的矩阵组成是先行再列的,所以Unity的TBN矩阵为
[ T x T y T z B x B y B z N x N y N z ] \begin{bmatrix} T_x&T_y&T_z\\ B_x&B_y&B_z\\ N_x&N_y&N_z \end{bmatrix} TxBxNxTyByNyTzBzNz
引用
用的别的大佬的,下面放一下链接:








 文章介绍了在OpenGL中处理法线向量的重要性,特别是在环境映射和光照计算中。法线矩阵,即模型-观测矩阵的逆转置,用于确保法线在变换后仍垂直于表面。文章讨论了错误地直接使用模型-观测矩阵变换法线的问题,以及为何需要转置和逆矩阵。此外,还讲解了TBN空间的概念,它是由切线、副切线和法线构成的局部坐标系统,用于处理法线贴图,TBN矩阵用于在不同空间之间转换法线向量。
文章介绍了在OpenGL中处理法线向量的重要性,特别是在环境映射和光照计算中。法线矩阵,即模型-观测矩阵的逆转置,用于确保法线在变换后仍垂直于表面。文章讨论了错误地直接使用模型-观测矩阵变换法线的问题,以及为何需要转置和逆矩阵。此外,还讲解了TBN空间的概念,它是由切线、副切线和法线构成的局部坐标系统,用于处理法线贴图,TBN矩阵用于在不同空间之间转换法线向量。














 6649
6649











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








