张量分解基础

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

本文主要对张量的基于pytorch的基础操作以及张量的CP分解、Tucker分解的关键知识点总结。

---

张量变换基础

1.Reshape

torch.reshape()可以对张量的各个维度的大小进行变换，但总的维度大小需保存不变。

import torch
a = torch.arange(4.)
b = torch.arange(4.)
##用法一
a = torch.reshape(a, (2, 2))
print(a.shape)
print(a)
##用法二
b = b.reshape(2,2)
print(b.shape)
print(b)

2.permute

对矩阵维度之间的交换。
torch.permute(input, dims) → Tensor

import torch
c=torch.arange(24)
c=c.reshape(2,3,4)
print('c:\n',c)
print('c.shape',c.shape)
d = torch.permute(c,(2,0,1)) #index 0和index 2交换
e = c.permute(2,0,1) #也可以这么用
print('d.shape',d.shape)
print('d\n',d)
print('e.shape',e.shape)
print('e\n',e)

输出结果如下：

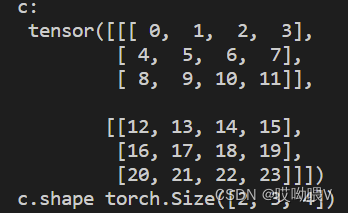
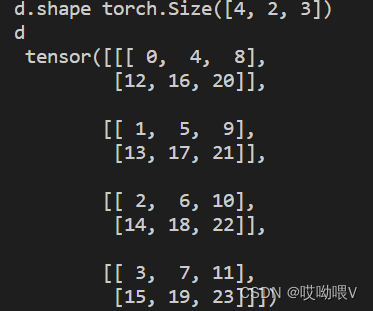
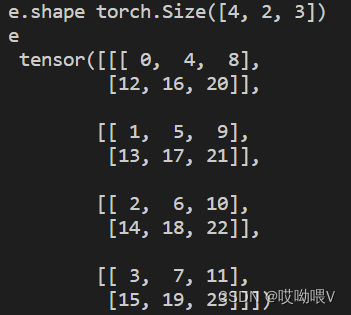
2.einsum

这是张量计算非常强大非常重要的一个函数
torch.einsum(equation, *operands) → Tensor

（1）计算 trace(迹)

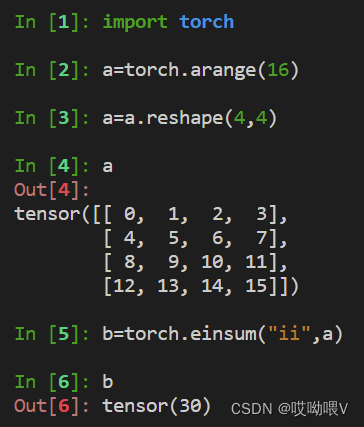
（2）计算diagonal，返回对角线

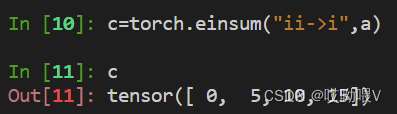
（3）计算外积(outer product)

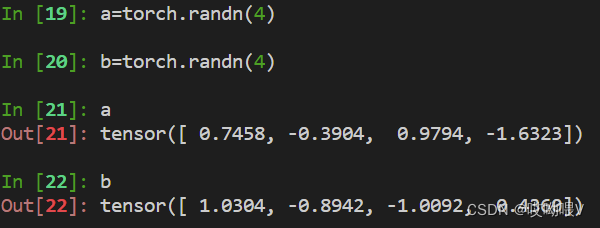
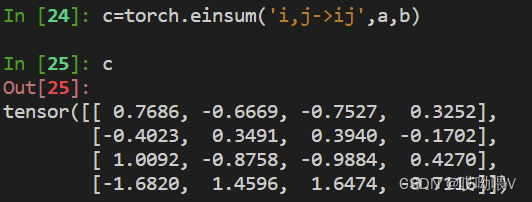
（4）张量相乘

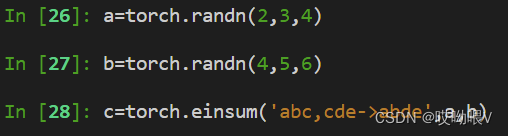
->右边消失的维度即时沿着该维度累加，例如‘abc,cde->abe’
例如在神经网络中，我们想进行batch计算

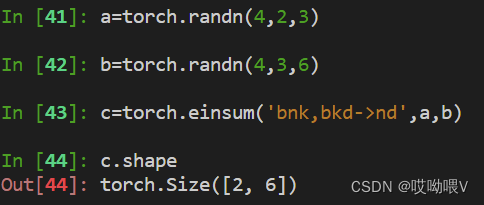
二、张量矩阵化

可以参考b站课程【张量网络PyThon编程：1.4 张量网络图形表示】
实际上就是把张量变成矩阵。对于三维张量，有张量按模式展开成矩阵，假设原来张量维度(i,j,k)。
模一张开即为(i,j,k)->(i,jk)
模二展开即为(i,j,k)->(j,ik)
模三展开即为(i,j,k)->(k,ij)

可参考如何简单地理解和实现「张量展开」

我们可以借助torch.reshape()函数实现。

三、张量分解

关于这部分的知识点来自于张量网络PyThon编程

1、单秩分解

将K阶张量分解为K个向量的直积。

$\mathbf{T}=\zeta {\prod }_{\otimes k=0}^{K-1}{\mathbf{v}}^{(k)}$

其中$\zeta$是一个标量系数。
由于大多数张量不存在严格的单秩分解，于是便有了最优单秩近似问题。

min ⁡ ζ , { ∣ v [ k ] ∣ = 1 } ∣ T − ζ ∏ ⊗ k = 0 K − 1 v ( k ) ∣ \min _{\zeta,\left\{\left|v^{[k]}\right|=1\right\}}\left|\boldsymbol{T}-\zeta \prod_{\otimes k=0}^{K-1} \boldsymbol{v}^{(k)}\right| minζ,{∣v[k]∣=1}​ ​T−ζ∏⊗k=0K−1​v(k) ​

通过对张量进行单秩分解，我们可以达到对参数进行压缩的目的。

2、CP分解(Canonical polyadic decomposition)

CP分解,是将张量分解为一系列秩一张量之和。
将单秩张量的形式稍作扩展，定义CP积，设N阶张量𝑇为𝑅 个单秩张量的求和：

$\mathcal{T}={\sum }_{r=0}^{R-1}{T}^{(r-1)}={\sum }_{r=0}^{R-1}{\zeta }^{(r)}{\prod }_{\otimes k=0}^{K-1}{\mathbf{v}}^{(r,k)}$

将${\zeta }^{(r)}$看成向量,${\mathbf{v}}^{(r,k)}$看成矩阵，则上式的CP形式也可写成如下的形式：

$\mathcal{T}={\sum }_{r=0}^{R-1}{\mathbf{\zeta }}_r{\prod }_{\otimes k=0}^{K-1}{\mathbf{V}}_{(r,a_n)}^{(k)}$

其中，$\mathbf{\zeta }$为R维向量，$V^{(n)}$为对应于第n个指标的矩阵，由R个列向量组成。

例如给定一个三维张量$\mathcal{T}\in {\mathbb{R}}^{I\times J\times K}$，CP分解就是将其分解为

$\mathcal{T}={\sum }_{r=1}^R{\mathbf{v}}_r^1\circ {\mathbf{v}}_r^2\circ {\mathbf{v}}_r^3$

(在此$\zeta$没有提取出来)其中${\mathbf{v}}_r^1\circ {\mathbf{v}}_r^2\circ {\mathbf{v}}_r^3$对应一个秩一张量，${\mathbf{v}}_r^1\in {\mathbb{R}}^I$，${\mathbf{v}}_r^2\in {\mathbb{R}}^J$,${\mathbf{v}}_r^3\in {\mathbb{R}}^K$是第r个分量的三种模态的分解向量。

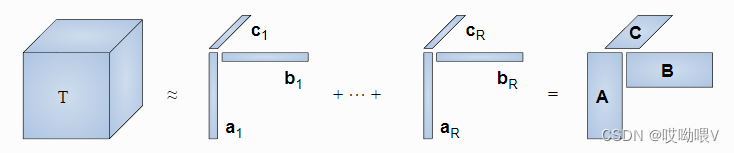
建议想进一步了解可以参考知乎-矩阵分析

3、Tucker分解

Tucker分解，又称高阶奇异值分解（Higher-order singular value decomposition，简称HOSVD），是主成分分析(PCA)的高阶形式。

（1）PCA

它的目的是为了用k个主分量概况表达统计相关的n个特征，即，主分量分析就是要在$C^n$空间中寻找 k个正交基，这k个正交基构成了我们想要的低维子空间。它的做法为对原数据矩阵X的协方差矩阵C进行特征分解，并将特征向量按行排列降序排列得到变换矩阵P，Y=PX 便是是要求的低维矩阵，其中P中的特征向量并不是全部特征向量，我们选取特征值较大的前几个特征向量组成P以达到降维效果。知乎-[PCA分解]

（2）Tucker分解

Tucker分解是将高阶张量分解为一个和它同阶的核心张量以及若干变换矩阵。
$T_{i_0\dots i_{N-1}}={\sum }_{j_0\dots j_{N-1}}{G}_{j_0\dots j_{N-1}}{\prod }_{n=0}^{N-1}{U}_{i_n{j}_n}^{(n)}$

约束条件

①G称为核心张量，其各个指标的约化矩阵(reduced matrix)必须为非负实对角矩阵。

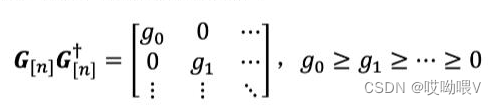
$G_{[}n]$模n展开。

②变换矩阵{$U^{(n)}$}满足幺正条件$U^{(n)}{U}^{(n)\ast }=U^{(n)\ast }{U}^{(n)}=I$

求解方法

①对$T_{[n]}$通过奇异值分解获得变换矩阵:$U^{(n)}{S}^{(n)}{V}^{(n)\ast }$

②核张量满足：$G_{i_0\dots i_{N-1}}={\sum }_{j_0\dots j_{N-1}}{T}_{j_0\dots j_{N-1}}{\prod }_{n=0}^{N-1}{U}_{j_n{i}_n}^{(n)\ast }$

③$T_{[n]}$的秩构成的Tucker秩(所以Tucker秩应该有N-1个)
如果我们对Tucker秩们取低秩近似的话，就实现了压缩。

回顾单秩分解，可知单秩张量的Tucker秩为(1, 1, …, 1)
（建议参考【知乎-CP分解与Tucker分解详解】)