example:根据学生的两门成绩,判断是否会被大学accepted。
data:
34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
95.86155507093572,38.22527805795094,0
75.01365838958247,30.60326323428011,0
82.30705337399482,76.48196330235604,1
69.36458875970939,97.71869196188608,1
39.53833914367223,76.03681085115882,0
53.9710521485623,89.20735013750205,1
69.07014406283025,52.74046973016765,1
67.94685547711617,46.67857410673128,0
70.66150955499435,92.92713789364831,1
76.97878372747498,47.57596364975532,1
67.37202754570876,42.83843832029179,0
89.67677575072079,65.79936592745237,1
50.534788289883,48.85581152764205,0
34.21206097786789,44.20952859866288,0
77.9240914545704,68.9723599933059,1
62.27101367004632,69.95445795447587,1
80.1901807509566,44.82162893218353,1
93.114388797442,38.80067033713209,0
61.83020602312595,50.25610789244621,0
38.78580379679423,64.99568095539578,0
61.379289447425,72.80788731317097,1
85.40451939411645,57.05198397627122,1
52.10797973193984,63.12762376881715,0
52.04540476831827,69.43286012045222,1
40.23689373545111,71.16774802184875,0
54.63510555424817,52.21388588061123,0
33.91550010906887,98.86943574220611,0
64.17698887494485,80.90806058670817,1
74.78925295941542,41.57341522824434,0
34.1836400264419,75.2377203360134,0
83.90239366249155,56.30804621605327,1
51.54772026906181,46.85629026349976,0
94.44336776917852,65.56892160559052,1
82.36875375713919,40.61825515970618,0
51.04775177128865,45.82270145776001,0
62.22267576120188,52.06099194836679,0
77.19303492601364,70.45820000180959,1
97.77159928000232,86.7278223300282,1
62.07306379667647,96.76882412413983,1
91.56497449807442,88.69629254546599,1
79.94481794066932,74.16311935043758,1
99.2725269292572,60.99903099844988,1
90.54671411399852,43.39060180650027,1
34.52451385320009,60.39634245837173,0
50.2864961189907,49.80453881323059,0
49.58667721632031,59.80895099453265,0
97.64563396007767,68.86157272420604,1
32.57720016809309,95.59854761387875,0
74.24869136721598,69.82457122657193,1
71.79646205863379,78.45356224515052,1
75.3956114656803,85.75993667331619,1
35.28611281526193,47.02051394723416,0
56.25381749711624,39.26147251058019,0
30.05882244669796,49.59297386723685,0
44.66826172480893,66.45008614558913,0
66.56089447242954,41.09209807936973,0
40.45755098375164,97.53518548909936,1
49.07256321908844,51.88321182073966,0
80.27957401466998,92.11606081344084,1
66.74671856944039,60.99139402740988,1
32.72283304060323,43.30717306430063,0
64.0393204150601,78.03168802018232,1
72.34649422579923,96.22759296761404,1
60.45788573918959,73.09499809758037,1
58.84095621726802,75.85844831279042,1
99.82785779692128,72.36925193383885,1
47.26426910848174,88.47586499559782,1
50.45815980285988,75.80985952982456,1
60.45555629271532,42.50840943572217,0
82.22666157785568,42.71987853716458,0
88.9138964166533,69.80378889835472,1
94.83450672430196,45.69430680250754,1
67.31925746917527,66.58935317747915,1
57.23870631569862,59.51428198012956,1
80.36675600171273,90.96014789746954,1
68.46852178591112,85.59430710452014,1
42.0754545384731,78.84478600148043,0
75.47770200533905,90.42453899753964,1
78.63542434898018,96.64742716885644,1
52.34800398794107,60.76950525602592,0
94.09433112516793,77.15910509073893,1
90.44855097096364,87.50879176484702,1
55.48216114069585,35.57070347228866,0
74.49269241843041,84.84513684930135,1
89.84580670720979,45.35828361091658,1
83.48916274498238,48.38028579728175,1
42.2617008099817,87.10385094025457,1
99.31500880510394,68.77540947206617,1
55.34001756003703,64.9319380069486,1
74.77589300092767,89.52981289513276,1
其中0代表not accepted,1代表accepted。
数据的大概:

以EXAM1为横轴,以EXAM2为纵轴,画出录取和未被录取的点的分布。



定义一个获取原始数据的函数。
data.insert(0,'ones',1)
是在第一列的位置插入全是1的一列,列名为’ones’,因为我们的
x
x
x的第一个分量是1。
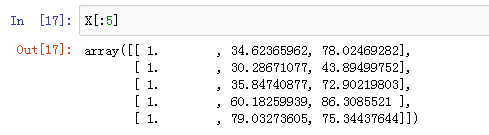
我们的
x
x
x最终长这个样子:
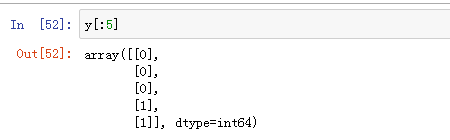
y
y
y取的是最后一列:
然后定义sigmoid函数:

接下来是cost function:
 我们在这里全部使用矩阵乘法,因为这样很方便(这叫向量化)。
我们在这里全部使用矩阵乘法,因为这样很方便(这叫向量化)。
A=sigmoid(X@theta)
中的@符号就是矩阵乘法的意思。
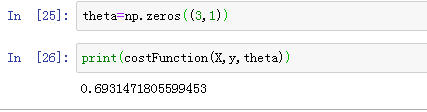
随便初始化一个
θ
\theta
θ,我们得到一个cost:
下面是最重要的梯度下降法了。
为了向量化,我们先做些准备:
令
x
=
[
1
x
1
(
1
)
x
2
(
1
)
⋯
x
n
(
1
)
1
x
1
(
2
)
x
2
(
2
)
⋯
x
n
(
2
)
⋮
⋮
⋮
⋯
⋮
1
x
1
(
m
)
x
2
(
m
)
⋯
x
n
(
m
)
]
x=\begin{bmatrix}1&x_1^{(1)}&x_2^{(1)}&\cdots&x_n^{(1)}\\1&x_1^{(2)}&x_2^{(2)}&\cdots&x_n^{(2)}\\\vdots&\vdots&\vdots&\cdots&\vdots\\1&x_1^{(m)}&x_2^{(m)}&\cdots&x_n^{(m)}\end{bmatrix}
x=⎣⎢⎢⎢⎢⎡11⋮1x1(1)x1(2)⋮x1(m)x2(1)x2(2)⋮x2(m)⋯⋯⋯⋯xn(1)xn(2)⋮xn(m)⎦⎥⎥⎥⎥⎤
x x x有 m m m个样本,每个样本有 n + 1 n+1 n+1个特征。
θ = [ θ 0 θ 1 ⋮ θ n ] \theta=\begin{bmatrix}\theta_0\\\theta_1\\\vdots\\\theta_n\end{bmatrix} θ=⎣⎢⎢⎢⎡θ0θ1⋮θn⎦⎥⎥⎥⎤
y = [ y ( 1 ) y ( 2 ) ⋮ y ( m ) ] y=\begin{bmatrix}y^{(1)}\\y^{(2)}\\\vdots\\y^{(m)}\end{bmatrix} y=⎣⎢⎢⎢⎡y(1)y(2)⋮y(m)⎦⎥⎥⎥⎤
我们知道梯度下降算法为:
θ j : = θ j − α m ∑ i = 1 m [ h ( i ) − y ( i ) ] x j ( i ) \theta_j:=\theta_j-\frac{\alpha}{m}\sum_{i=1}^m[h^{(i)}-y^{(i)}]x_j^{(i)} θj:=θj−mα∑i=1m[h(i)−y(i)]xj(i)
一个一个来更新
θ
j
\theta_j
θj就是这个样子:
θ
0
:
=
θ
0
−
α
m
∑
i
=
1
m
[
h
(
i
)
−
y
(
i
)
]
x
0
(
i
)
θ
1
:
=
θ
1
−
α
m
∑
i
=
1
m
[
h
(
i
)
−
y
(
i
)
]
x
1
(
i
)
θ
2
:
=
θ
2
−
α
m
∑
i
=
1
m
[
h
(
i
)
−
y
(
i
)
]
x
2
(
i
)
⋯
θ
n
:
=
θ
n
−
α
m
∑
i
=
1
m
[
h
(
i
)
−
y
(
i
)
]
x
n
(
i
)
\theta_0:=\theta_0-\frac{\alpha}{m}\sum_{i=1}^m[h^{(i)}-y^{(i)}]x_0^{(i)}\\\theta_1:=\theta_1-\frac{\alpha}{m}\sum_{i=1}^m[h^{(i)}-y^{(i)}]x_1^{(i)}\\\theta_2:=\theta_2-\frac{\alpha}{m}\sum_{i=1}^m[h^{(i)}-y^{(i)}]x_2^{(i)}\\\cdots\\\theta_n:=\theta_n-\frac{\alpha}{m}\sum_{i=1}^m[h^{(i)}-y^{(i)}]x_n^{(i)}
θ0:=θ0−mα∑i=1m[h(i)−y(i)]x0(i)θ1:=θ1−mα∑i=1m[h(i)−y(i)]x1(i)θ2:=θ2−mα∑i=1m[h(i)−y(i)]x2(i)⋯θn:=θn−mα∑i=1m[h(i)−y(i)]xn(i)
我们这样来写:
θ
:
=
θ
−
α
δ
\theta:=\theta-\alpha\delta
θ:=θ−αδ
因此
δ
=
[
1
m
∑
i
=
1
m
[
h
(
i
)
−
y
(
i
)
]
x
0
(
i
)
1
m
∑
i
=
1
m
[
h
(
i
)
−
y
(
i
)
]
x
1
(
i
)
⋯
1
m
∑
i
=
1
m
[
h
(
i
)
−
y
(
i
)
]
x
n
(
i
)
]
=
1
m
[
1
1
1
⋯
1
x
1
(
1
)
x
1
(
2
)
x
1
(
3
)
⋯
x
1
(
m
)
x
2
(
1
)
x
2
(
2
)
x
2
(
3
)
⋯
x
2
(
m
)
⋮
⋮
⋮
⋮
⋮
x
n
(
1
)
x
n
(
2
)
x
n
(
3
)
⋯
x
n
(
m
)
]
[
h
θ
(
x
(
1
)
)
−
y
(
1
)
h
θ
(
x
(
2
)
)
−
y
(
2
)
⋮
⋮
h
θ
(
x
(
m
)
)
−
y
(
m
)
]
=
1
m
x
T
(
h
−
y
)
\delta=\begin{bmatrix}\frac{1}{m}\sum_{i=1}^m[h^{(i)}-y^{(i)}]x_0^{(i)}\\\frac{1}{m}\sum_{i=1}^m[h^{(i)}-y^{(i)}]x_1^{(i)}\\\cdots\\\frac{1}{m}\sum_{i=1}^m[h^{(i)}-y^{(i)}]x_n^{(i)}\end{bmatrix}\\=\frac{1}{m}\begin{bmatrix}1&1&1&\cdots&1\\x_1^{(1)}&x_1^{(2)}&x_1^{(3)}&\cdots&x_1^{(m)}\\x_2^{(1)}&x_2^{(2)}&x_2^{(3)}&\cdots&x_2^{(m)}\\\vdots&\vdots&\vdots&\vdots&\vdots\\x_n^{(1)}&x_n^{(2)}&x_n^{(3)}&\cdots&x_n^{(m)}\end{bmatrix}\begin{bmatrix}h_{\theta}(x^{(1)})-y^{(1)}\\h_{\theta}(x^{(2)})-y^{(2)}\\\vdots\\\vdots\\h_{\theta}(x^{(m)})-y^{(m)}\end{bmatrix}\\=\frac{1}{m}x^T(h-y)
δ=⎣⎢⎢⎢⎡m1∑i=1m[h(i)−y(i)]x0(i)m1∑i=1m[h(i)−y(i)]x1(i)⋯m1∑i=1m[h(i)−y(i)]xn(i)⎦⎥⎥⎥⎤=m1⎣⎢⎢⎢⎢⎢⎢⎡1x1(1)x2(1)⋮xn(1)1x1(2)x2(2)⋮xn(2)1x1(3)x2(3)⋮xn(3)⋯⋯⋯⋮⋯1x1(m)x2(m)⋮xn(m)⎦⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎡hθ(x(1))−y(1)hθ(x(2))−y(2)⋮⋮hθ(x(m))−y(m)⎦⎥⎥⎥⎥⎥⎥⎤=m1xT(h−y)
注意我们的 x 0 = 1 x_0=1 x0=1
这样梯度下降算法的向量化就完成了。

这里的iters是迭代次数,你自己定。
给定学习率和迭代次数,我们会得到:

最终的
θ
\theta
θ与最小的cost:
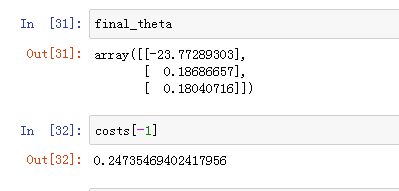
现在把decision boundary画出来:


最后做一个accuracy的评估,就是预测的准确率:























 3269
3269











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








