常微分方程（组）-简单欧拉法

努力的小流

已于 2024-06-12 15:17:57 修改

阅读量286

点赞数 8

分类专栏：微分方程文章标签：算法 matlab

于 2024-06-11 20:26:32 首次发布

本文链接：https://blog.csdn.net/weixin_43816345/article/details/139606790

版权

微分方程专栏收录该内容

2 篇文章 0 订阅

订阅专栏

一阶常微分方程欧拉法

考虑如下微分方程在[0, T]区间上的数值解：

$\frac{dy(t))}{dt}=f(y(t), t)$

$y(0)=y_0$

在[0, T]上取N个小区间，每个小区间长度为 $\vartriangle t=T/N$ ，共N+1个点，则 $t_1=0;......t_n=(n-1)\vartriangle t$

由泰勒展开：

$y(t_{n+1})=y(t_n+\vartriangle t) = y(t_n)+f(y(t_n),t)+o(\vartriangle t^2)$

即：

$y_{n+1}=y_n+f(y_n,t) \vartriangle t$

例题

$\frac{dy(t))}{dt}=y(t)$

$y(0)=1$

clear
T = 2; N = 10000; dt = T/N;
t = 0:dt:T;
y0 = 1;
y = zeros(1, length(t));
y(1) = y0;
for n = 1:length(t)-1
    y(n+1) = y(n) + y(n)*dt;
end
plot(t, y, t, exp(t))
legend('数值解','解析解')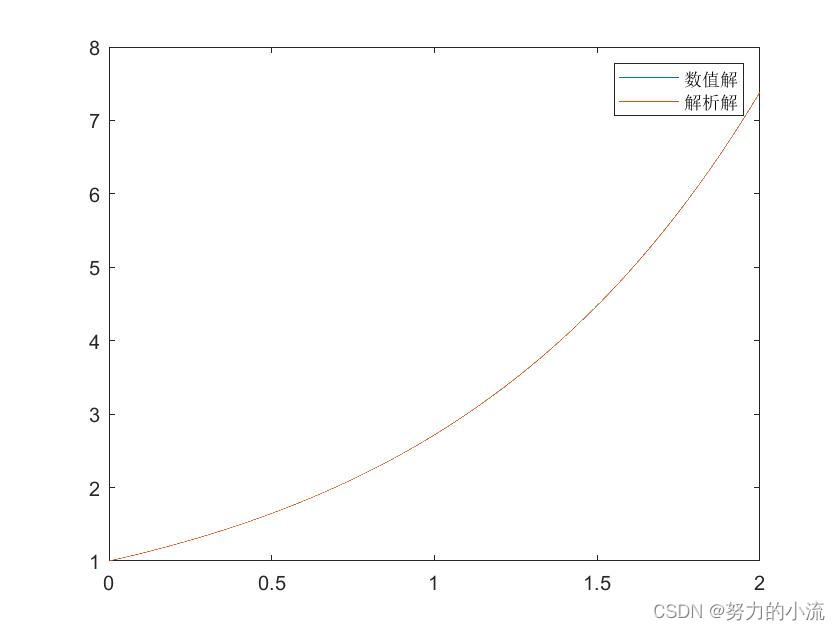

二阶常微分方程欧拉法

考虑如下常微分方程：

$\frac{d^2y}{dt^2}=f(y, \frac{dy}{dt}, t)$

$y(0)=y_0;\frac{dy}{dt}=v_0$

令：

$y_1(t) = y(t);y_2(t)=\frac{dy}{dt}(t)$

$\frac{dy_1}{dt}=y_2;\frac{dy_2}{dt}=f(y_1,y_2,t)$

例1谐振子

$\frac{d^2y}{dt^2}=-\frac{k}{m}y$

clear
k = 1; m=2;
T = 20; N = 10000; dt = T/N;
t = 0:dt:T;
y0 = 1; y1 = zeros(1, length(t)); y1(1) = y0;
v0 = 1; y2 = zeros(1, length(t)); y2(1) = v0;
for n = 1:length(t)-1
    y1(n+1) = y1(n) + y2(n)*dt;
    y2(n+1) = y2(n) + (-k/m*y1(n))*dt;
end
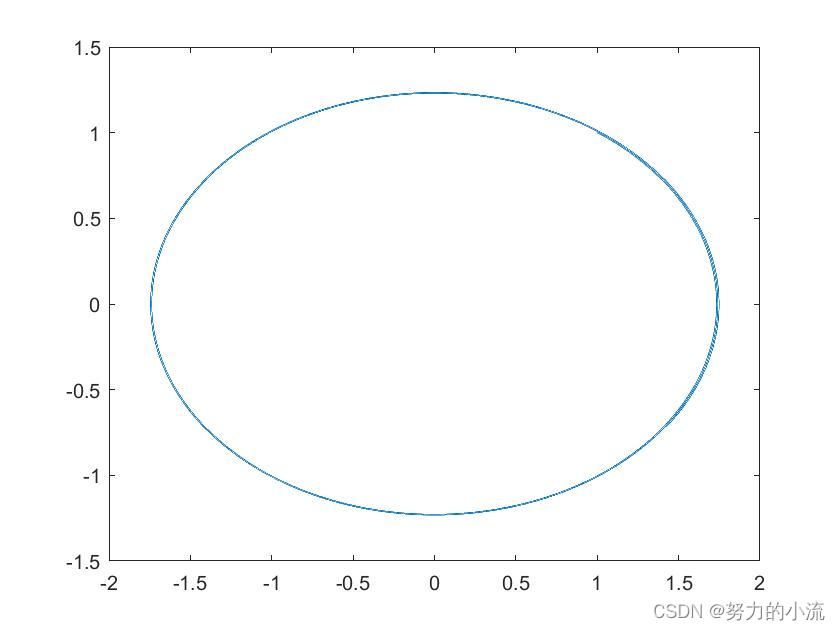
figure(1)
plot(t, y1, t, y2)
figure(2)
plot(y1, y2)

误差分析

回顾一下泰勒展开公式：

$y(t+\vartriangle t)=y(t)+y^{'}(t)\vartriangle t+\frac{1}{2}y^{''}(t)\vartriangle t^2+...+\frac{1}{n!}y^{(n)}(t)\vartriangle t+R_n$

$R_n = \frac{1}{(n+1)!}y^{(n+1)}(t)\vartriangle t^{n+1}=o(\vartriangle t^{n+1})$

这里有两个思想：

将泰勒展开公式看做是关于 $\vartriangle t$ 的无穷高阶多项式，利用多项式的形式和y(t)处的信息预测 $y(t+\vartriangle t)$ 处的值。
在第一个思想下， $\vartriangle t$ 越小，多项式阶数越高，则误差越小，其与 $\vartriangle t^{n+1}$ 成正比。

对于欧拉法

$\frac{dy(t))}{dt}=f(y(t), t)$

$y_{n+1}=y_n+f(y_n,t) \vartriangle t$

误差为 $o(\vartriangle t^2)$ ，而在代码中步长的选取是非常小的。

在使用简单欧拉法进行数值积分时，误差是会累积的，设一次计算的误差为 $\vartriangle t^2$ ，若在[0 1]区间上进行计算，则计算次数为 $1/\vartriangle t$ ，二者相乘，最终误差为步长。

努力的小流

关注

8
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
常微分方程（组）-简单欧拉法

在使用简单欧拉法进行数值积分时，误差是会累积的，设一次计算的误差为。在[0, T]上取N个小区间，每个小区间长度为。，若在[0 1]区间上进行计算，则计算次数为。，而在代码中步长的选取是非常小的。，二者相乘，最终误差为步长。
复制链接

扫一扫

专栏目录