样条和分段插值

最新推荐文章于 2025-03-17 15:31:44 发布

努力的小流

最新推荐文章于 2025-03-17 15:31:44 发布

阅读量1.9k

点赞数 57

分类专栏：曲线拟合文章标签：算法

本文链接：https://blog.csdn.net/weixin_43816345/article/details/138857595

版权

曲线拟合专栏收录该内容

5 篇文章

订阅专栏

样条导论

多项式插值对n个数据点采用n-1阶多项式进行插值，该多项式曲线能够捕捉数据点的所有变化，但高次多项式在一些情况下会产生震荡，尤其是在剧变区域附近。

1901年，Carl Runge发表了他对于高次多项式插值风险的研究，他给出了如下函数（现在称其为龙格函数）：

$f(x) = \frac{1}{1+25x^2}$

对其[-1,1]区间内分别取5,6,7,8,9,10,11个点进行插值，随着多项式次数的增加，震荡越来越剧烈，结果如下：

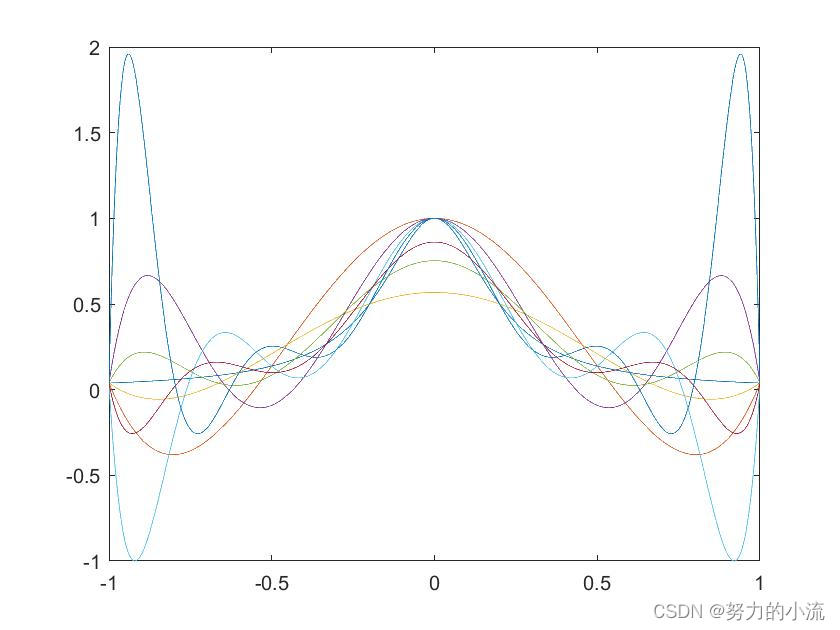
另一种插值方法是采用分段低次多项式对数据点的子集进行插值，这样的多项式称为样条函数。如果用三次曲线连接每对数据点，那么称为三次样条。同理还有一次样条、二次样条，但我们接下来会介绍三次样条的优越性。

问题描述

使用不同的样条函数拟合下表中的数据：

i	xi	fi
1	3	2.5
2	4.5	1
3	7	2.5
4	9	0.5

线性样条（一次样条）

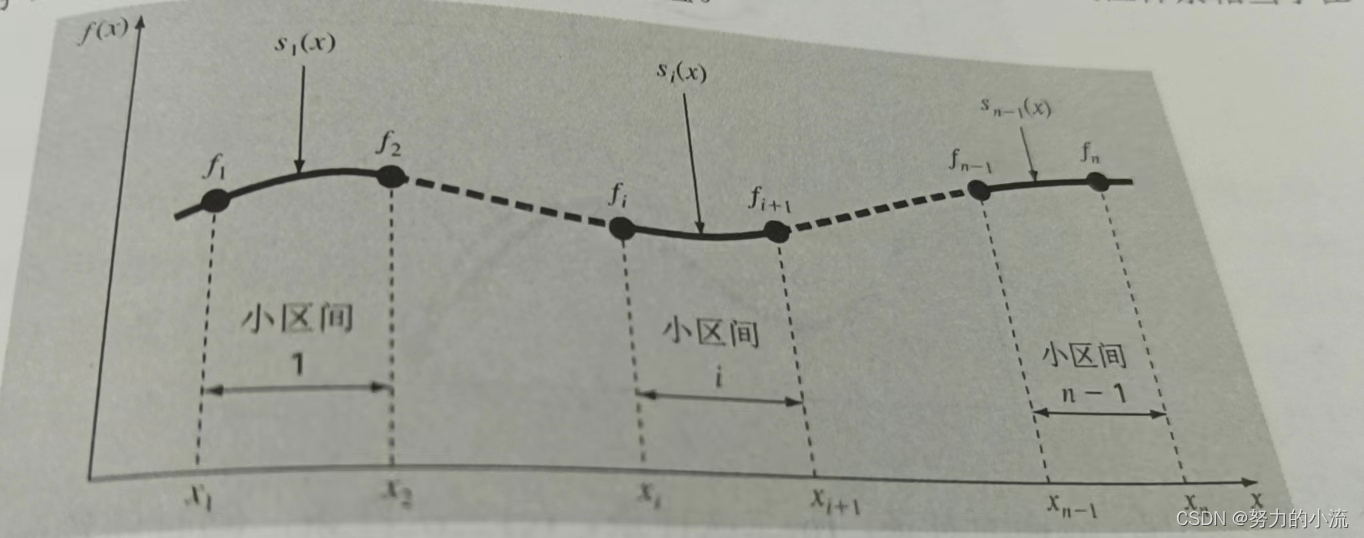
如图所示，给定n个数据点，将区间分成n-1份，每个小区间i都对应一个样条函数si(x)。对于线性样条来说：

$s_i(x) =a_i+b_i(x-x_i)$

其中：

$a_i = f_i$

$b_i = \frac{f_{i+1}-f_i}{x_{i+1}-x_i}$

插值结果如图所示：

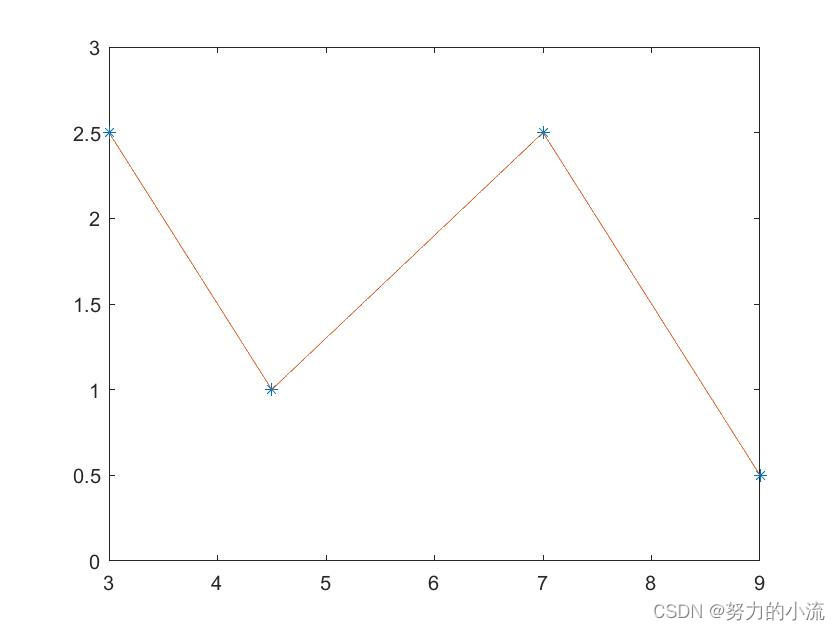
由图可知，一次样条最主要的缺点是不光滑，在两个样条的交点处，它的斜率发生了剧烈的变化。

三次样条

二次样条也存在其自身的缺点，我们直接跳过，介绍三次样条，它是实际中最常用的样条。三次样条要求节点处的一阶导数和二阶导数均相等，这就保证了曲线在整个区间上的光滑性。此外，四次或更高次的样条表现出高次多项式本身固有的不稳定性。这些原因使得三次样条插值成为最受欢迎的样条。

$s_(x) = a_i+b_i(x-x_i)+c_i(x-x_i)^2+d_i(x-x_i)^3$

给定n个数据点，共有n-1个区间，需要确定4(n-1)个未知系数。

条件1：样条通过所有数据点

将每一个区间左侧数据点代入得：

$a_i = f_i$ ，其中i取1...n-1，共得到n-1个方程。

条件2：三次多项式在节点处连续

对节点i+1：

$f_i+b_ih_i+c_ih_i^2+d_ih_i^3 = f_{i+1}$

其中i取1...n-1，共n-1个方程。

条件3：一阶导数在节点处处处相等

$s_i^{'}(x) = b_i+2c_i(x-x_i)+3d_i(x-x_i)$

于是内部节点在i+1处导数相等的条件表示为

$b_i+2c_ih_i+3d_ih_i^2 = b_{i+1}$ ，其中i取1...n-2，共n-2个方程。 $h_{i-1}c_{i-1}+2(h_{i-1}-h_i)c_i+h_ic_{i+1} = 3\frac{f_{i+1}-f_i}{h_i}-3\frac{f_i-f_{i-1}}{h_{i-1}}$

条件4：二阶导数在节点处相等

$s_i^{''}(x) = 2c_i+6d_i(x-x_i)$

于是，内部节点在i+1处二阶导数相等的条件可表示为：

$c_i+3d_ih_i = c_{i+1}$ ，其中i取1...n-2，共n-2个方程。

联立上述条件可得以下方程：

$a_i = f_i$

$b_i = \frac{f_{i+1}-f_i}{h_i} - \frac{h_i}{3}(2c_i+c_{i+1})$

$d_i = \frac{c_{i+1}-c_i}{3h_i}$

$h_{i-1}c_{i-1}+2(h_{i-1}-h_i)c_i+h_ic_{i+1} = 3\frac{f_{i+1}-f_i}{h_i}-3\frac{f_i-f_{i-1}}{h_{i-1}}$

最后一个方程在内部节点2...n-2处均成立。因此只需要添加两个边界条件，就可以解出c，利用c可以计算得出b和d。

边界条件

三次样条具有不同的边界条件选取方法：

自然样条，即假设端点的二阶导数等于0；
固定边界条件：指定第一和最后一个结点处的一阶导数值；（如果我们能够事先知道真实的一阶导数值，那么固定样条的拟合结果则会变得很好）
“非结点”边界条件：第二和倒数第二个结点处的三阶导数连续（即前两个和最后两个相邻区域中使用相同的三次函数）。

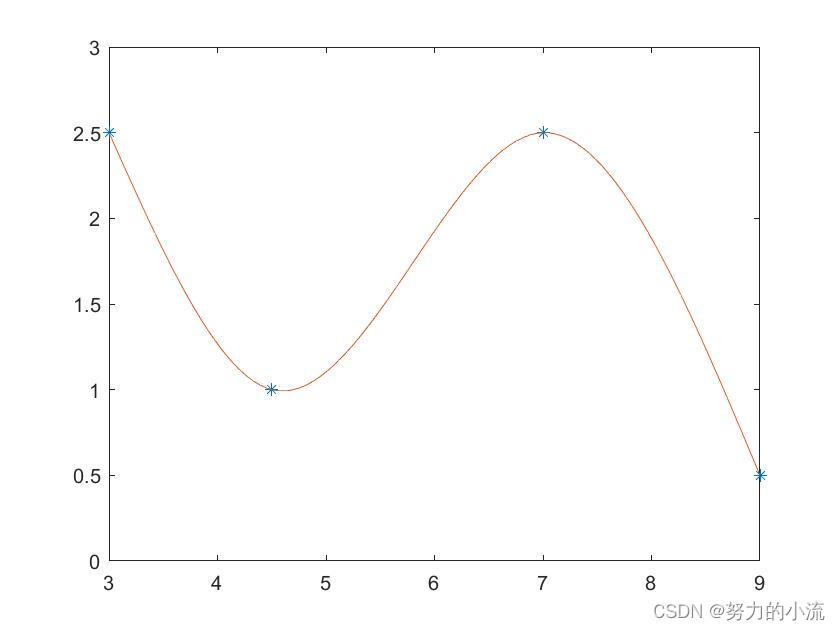
手搓自然样条：

clear
clc
% 线性样条插值
x = [3, 4.5, 7, 9];
y = [2.5, 1, 2.5, 0.5];

xx = linspace(x(1), x(end));
[yy, dy, d2] = natspline(x, y, xx);
plot(x, y, '*', xx, yy)
ylim([0, 3])

function [yy, dy, d2] = natspline(x, y, xx)
% 样条插值，（自然边界）
% input:
% x：待插值自变量
% y：待插值因变量
% xx：待计算的点
% output
% yy；在xx处的值
% dy：在xx处的一阶导数值
% d2：在xx处的二阶导数值
n = length(x);
m = length(xx);
b = zeros(n,n);

% 计算方程中的A，B矩阵
A(1,1) = 1; A(n,n) = 1;
B(1) = 0; B(n) = 0;
for i = 2:n-1
    A(i, i-1) = h(x, i-1);
    A(i, i) = 2*(h(x, i-1) + h(x, i));
    A(i, i+1) = h(x, i);
    B(i) = 3*(fd(i+1, i, x, y) - fd(i, i-1, x, y));
end
% 计算参数a、b、c、d
c = A\B';
for i = 1:n-1
    a(i) = y(i);
    b(i) = fd(i+1, i, x, y) - h(x, i)/3 * (2*c(i) + c(i+1));
    d(i) = (c(i+1) - c(i)) / 3 / h(x, i);
end
% 计算插值点的值、一阶导数、二阶导数
yy = zeros(length(xx), 1); dy = zeros(length(xx), 1); d2 = zeros(length(xx), 1);
for i = 1:m
    [yy(i), dy(i), d2(i)] = SplineInterp(x, n, a, b, c, d, xx(i));
end
end
function hh = h(x, i)
% 计算小区间长度
hh = x(i+1) - x(i);
end
function fdd = fd(i, j, x, y)
% 计算差分
fdd = (y(i) - y(j)) / (x(i) - x(j));
end
function [yyy,dyy,d2y] = SplineInterp(x, n, a, b, c, d, xi)
% 首先定位xi所在区间，然后计算插值、一阶导数、二阶导数
for ii = 1:n-1
    if xi>=x(ii) - 0.000001 && xi <= x(ii+1)+0.000001
        yyy = a(ii)+b(ii)*(xi - x(ii)) + c(ii)*(xi - x(ii))^2 + d(ii)*(xi-x(ii))^3;
        dyy = b(ii) + 2*c(ii)*(xi-x(ii)) + 3*d(ii)*(xi - x(ii))^2;
        d2y = 2*c(ii) + 6*d(ii)*(xi-x(ii));
        break
    end
end
end