（图论专题）【网络最大流】

最新推荐文章于 2023-11-23 18:50:46 发布

九羽-

最新推荐文章于 2023-11-23 18:50:46 发布

阅读量309

点赞数

分类专栏：算法树之图论

本文链接：https://blog.csdn.net/weixin_43828245/article/details/102821610

版权

算法树之图论专栏收录该内容

15 篇文章 0 订阅

订阅专栏

（图论专题）【网络最大流】

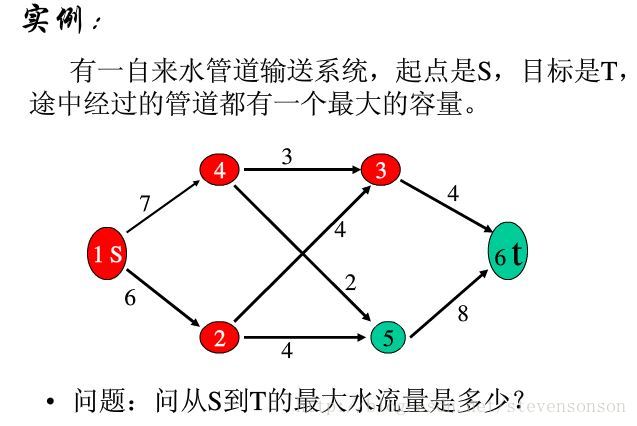
这里写图片描述

网络流图是一张只有一个源点和汇点的有向图，而最大流就是求源点到汇点间的最大水流量，下图的问题就是一个最基本，经典的最大流问题

这里写图片描述

题目链接：https://www.luogu.org/problem/P3376

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入格式

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式

一行，包含一个正整数，即为该网络的最大流。

输入样例 #1

输出样例 #1

代码：

/*
之前的模板有些问题，现在更新了一下。
1.最终要的一个更新：在dfs中及时break。
当sum==flow就是，当前的流已经流满了，直接break掉
2.当前弧优化
在bfs里cur复制head数组， 在dfs里用cur数组并且更新cur数组。
https://www.luogu.org/problem/P3386 这个题不优化就会T
*/
#include <bits/stdc++.h>

using namespace std;

struct node {
    int to,f,nxt;
};
const int maxn = 2e6+10;
node e[maxn];
int n,m,s,t;
int head[maxn];
int cur[maxn];
int dep[maxn];
int cnt;

void addage( int u, int v, int f )
{
    e[cnt].to = v;
    e[cnt].f = f;
    e[cnt].nxt = head[u];
    head[u] = cnt++;
}

int bfs(int node)
{
    memset(dep,0,sizeof(dep));
    memcpy(cur,head,sizeof(cur)); // 复制head数组
    dep[node] = 1;
    queue <int> Q;
    Q.push(node);
    while ( !Q.empty() ) {
        int x = Q.front();Q.pop();
        for ( int i=head[x]; i!=-1; i=e[i].nxt ) {
            int y = e[i].to,f = e[i].f;
            if ( !dep[y] && f ) {
                dep[y] = dep[x] + 1;
                Q.push(y);
            }
        }
    }
    return dep[t]; // return dep[t] ， 如果是0那么说明没有增广路了，退出while
}

int dfs( int x, int flow ) // dfs找增广路
{
    if ( x==t ) {
        return flow;
    }
    int sum = 0;
    for ( int i=cur[x]; i!=-1; i=e[i].nxt ) {
        cur[x] = i;
        int y = e[i].to, f = e[i].f;
        if ( f && dep[y]==dep[x]+1 ) {
            int t = dfs(y,min(flow-sum,f)); // 优化1
            sum += t;
            e[i].f -= t;
            e[i^1].f += t;
            if ( sum==flow ) break; // 优化1
        }
    }
    if ( sum==0 ) { // 如果sum==0，那么这个点之前没有增广路，深度清零
        dep[x] = 0;
    }
    return sum;
}

int main()
{
    scanf("%d %d %d %d",&n,&m,&s,&t);
    memset(head,-1,sizeof(head));
    cnt = 0;
    while ( m-- ) {
        int u,v,f;
        scanf("%d %d %d",&u,&v,&f);
        addage(u,v,f); addage(v,u,0);
    }
    int ans = 0;
    while ( bfs(s) ) { // 如果还存在增广路继续
        ans += dfs(s,0x3f3f3f3f); // 加一条增广路的值
    }
    printf("%d",ans);

    return 0;
}

例题1 Dining POJ - 3281

Cows are such finicky eaters. Each cow has a preference for certain foods and drinks, and she will consume no others.

Farmer John has cooked fabulous meals for his cows, but he forgot to check his menu against their preferences. Although he might not be able to stuff everybody, he wants to give a complete meal of both food and drink to as many cows as possible.

Farmer John has cooked F (1 ≤ F ≤ 100) types of foods and prepared D (1 ≤ D ≤ 100) types of drinks. Each of his N (1 ≤ N ≤ 100) cows has decided whether she is willing to eat a particular food or drink a particular drink. Farmer John must assign a food type and a drink type to each cow to maximize the number of cows who get both.

Each dish or drink can only be consumed by one cow (i.e., once food type 2 is assigned to a cow, no other cow can be assigned food type 2).

Input

Line 1: Three space-separated integers: N, F, and D
Lines 2.. N+1: Each line i starts with a two integers Fi and Di, the number of dishes that cow i likes and the number of drinks that cow i likes. The next Fi integers denote the dishes that cow i will eat, and the Di integers following that denote the drinks that cow i will drink.

Output

Line 1: A single integer that is the maximum number of cows that can be fed both food and drink that conform to their wishes

Sample Input

4 3 3
2 2 1 2 3 1
2 2 2 3 1 2
2 2 1 3 1 2
2 1 1 3 3

Sample Output

Hint

One way to satisfy three cows is:
Cow 1: no meal
Cow 2: Food #2, Drink #2
Cow 3: Food #1, Drink #1
Cow 4: Food #3, Drink #3
The pigeon-hole principle tells us we can do no better since there are only three kinds of food or drink. Other test data sets are more challenging, of course.

题意：有N头牛，F种食物，D种饮料，每头牛都有自己喜欢的食物和饮料，每种饮料和食物只能分配给一头牛。问：最多有多少头牛能同时得到自己喜欢的食物和饮料。

思路：最大流建图是把食物和饮料放在两端。一头牛拆分成两个点，两点之间的容量为1.喜欢的食物和饮料跟牛建条边，容量为1.加个源点和汇点。源点与食物、饮料和汇点的边容量都是1，表示每种食物和饮料只有一个。这样话完全是最大流问题了。

建图：从源点向每个食物连一条边，容量为1，
将牛拆成两个点牛，牛'，中间连边，容量为1
从食物向牛连边，容量为1
连牛'和饮料，容量为1
连饮料和汇点，容量为1

源点-->food-->牛(左)-->牛(右)-->drink-->汇点

图解：

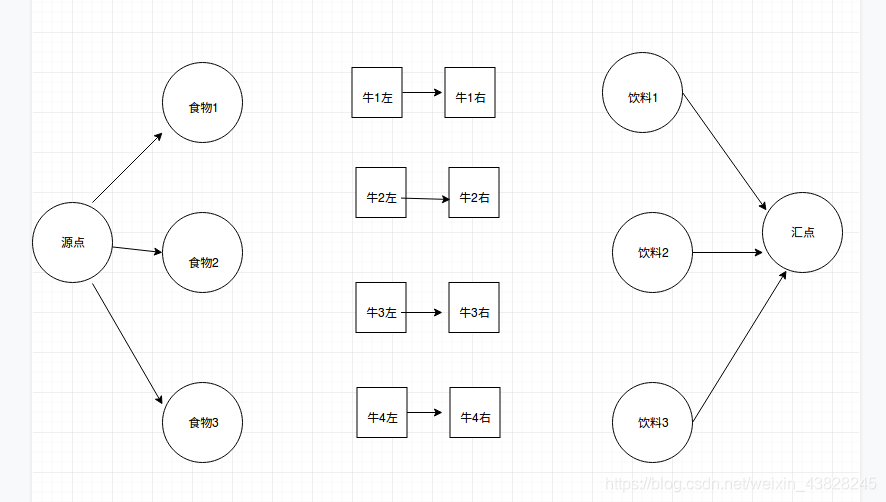
再加上食物饮料和牛的关系，跑一边源点到汇点的最大流dinic算法就得到答案了。

代码：

#include <iostream>
#include <queue>
#include <cstring>
#include <stdio.h>

using namespace std;

struct node {
    int to,w,nxt;
};
const int maxn = 2e5+10;
node e[maxn];
int n,f,d;
int head[maxn];
int dep[maxn];
int cnt;

void addage( int u, int v, int w )
{
    e[cnt].to = v;
    e[cnt].w = w;
    e[cnt].nxt = head[u];
    head[u] = cnt++;
}

int bfs(int node) // bfs分层
{
    memset(dep,0,sizeof(dep)); // dep 层的深度
    dep[node] = 1;
    queue <int> Q;
    Q.push(node);
    while ( !Q.empty() ) {
        int x = Q.front();Q.pop();
        for ( int i=head[x]; i!=-1; i=e[i].nxt ) {
            int y = e[i].to,w = e[i].w;
            if ( !dep[y] && w ) {
                dep[y] = dep[x] + 1; // 编号++
                Q.push(y);
            }
        }
    }
    return dep[f+d+2*n+1]; // return dep[t] ， 如果是0那么说明没有增广路了，退出while
}

int dfs( int x, int flow ) // dfs找增广路
{
    if ( x==f+d+2*n+1 ) {
        return flow;
    }
    int sum = 0;
    for ( int i=head[x]; i!=-1; i=e[i].nxt ) {
        int y = e[i].to, w = e[i].w;
        if ( w && dep[y]==dep[x]+1 ) {
            int t = dfs(y,min(flow,w));// 注意dfs里面的是min(flow，w)
            flow -= t;      // 当前的flow减t
            sum+=t;         // sum加t，就是上面减去的t。
            e[i].w -= t;    // 正向边减t
            e[i^1].w += t;  // 反向边加t
        }
    }
    if ( sum==0 ) { // 如果sum==0，那么这个点之前没有增广路，深度清零
        dep[x] = 0;
    }
    return sum;
}

int main()
{
    int i,j,u,v,w;
    cnt = 0;
    memset(head,-1,sizeof(head));
    cin >> n >> f >> d;
    // 源点0， 食物1~f, 饮料f+1~f+d, 牛f+d+1~f+d+2*n, 汇点f+d+2*n+1
    for ( i=1; i<=f; i++ ) { // 建立源点和食物的关系
        addage(0,i,1);
        addage(i,0,0);
    }
    for ( i=1; i<=d; i++ ) { // 建立饮料与汇点的关系
        addage(f+i,f+d+2*n+1,1);
        addage(f+d+2*n+1,f+i,0);
    }
    for ( i=f+d+1; i<=f+d+2*n; i+=2 ) { // 建立牛之间的关系
        addage(i,i+1,1);
        addage(i+1,i,0);
    }
    for ( i=0; i<n; i++ ) {
        int ai,bi,x;
        cin >> ai >> bi;
        for ( j=0; j<ai; j++ ) { // 建立食物和左牛的关系
            cin >>x;
            addage(x,f+d+1+2*i,1);
            addage(f+d+1+2*i,x,0);

        }
        for ( j=0; j<bi; j++ ) { // 建立右牛和饮料的关系
            cin >>x;
            addage(f+d+2+2*i,f+x,1);
            addage(f+x,f+d+2+2*i,0);
        }
    }

    int ans = 0;
    while ( bfs(0) ) { // 如果还存在增广路继续
        ans += dfs(0,0x3f3f3f3f); // 加一条增广路的值
    }
    printf("%d\n",ans);

    return 0;
}

例题2 ： The Berland Championship Gym - 100694F

题意：这里有n个学生和m道题，第二行表示第i个学生最多能做几道题，接下来是每个学生的名字，再有一个01矩阵，行代表学生，列代表题号，1就是会做，0是不会做。现在让你挑出3个学生要求他们能解出的题目最多。

Examples Input

5 5
3 2 2 3 1
Slava
Andrew
Egor
Denis
Sergey
11011
10100
00001
00100
10000

Output

5
Slava Andrew Egor

思路：刚开始想到的就是网络流，s和学生连接，学生和他能解的题目连接，题目和t连接。但是 Time limit exceeded on test 10 ，显然不能这样建图，看到大神的博客提出，将题目给划分成8个集合，这样1000道题目，1000个点就可以简化为8个点了，跑8个点肯定不会超时。

000（没有人可以做出的问题数量）

001（第一个人可以单独做出的问题数量）

010（第二个人可以单独做出的问题数量）

100（第三个人可以单独做出的问题数量）

011（第一个人和第二个人都可以做出的问题数量）

101（第一个人和第三个人都可以做出的问题数量）

110（第三个人和第二个人都可以做出的问题数量）

111（第一二三个人都可以做出的问题数量）
将每个点都抽象出一个值来，正好对应上面8个值，方法是：如果第一个人会做tem+1，如果第二个人会做tem+2，如果第三个人会做tem+4，最后用一个now数组来记录每种类型的题目有几个。

建图方式：源点s和三个学生连接，流量为学生最多能解的题目；三个学生和八个类型的题连接，流量为这种题的个数；八种题和汇点t连接，流量为这种题的个数。

注意：在前向星存图的时候直接在一个函数里把正反边都建出来，这题就因为反边写错了wa了十几遍，还有注意反边的流量是零。

还有一个很玄学的地方，数组开了2e5跑了1825ms，开2e4的数组只跑了249ms

代码：

#include <bits/stdc++.h>

using namespace std;

const int maxn = 2e5+10;
struct node {
    int to,nxt,f;
}e[maxn];

int head[maxn],dep[maxn];
int now[10];
int s,t;
int student, problem;
string name[55];
int solve[55];
int cnt;
int a[55][1111];

void addage( int u, int v, int f )
{
    e[cnt].to = v;
    e[cnt].f = f;
    e[cnt].nxt = head[u];
    head[u] = cnt++;
    
    e[cnt].to = u;
    e[cnt].f = 0;   // 这个地方是0！！！
    e[cnt].nxt = head[v];
    head[v] = cnt++;
}

int bfs( int v0 )
{
    memset(dep,0,sizeof(dep));
    queue <int> Q;
    dep[v0] = 1;
    Q.push(v0);
    while ( !Q.empty() ) {
        int x = Q.front(); Q.pop();
        for ( int i=head[x]; i!=-1; i=e[i].nxt ) {
            int y = e[i].to, f=e[i].f;
            if ( f&&dep[y]==0 ) {
                dep[y] = dep[x] + 1;
                Q.push(y);
            }
        }
    }
    return dep[t];
}

int dfs( int x, int flow )
{
    if ( x==t ) {
        return flow;
    }
    int sum = 0;
    for ( int i=head[x]; i!=-1; i=e[i].nxt ) {
        int y = e[i].to, f=e[i].f;
        if ( f&&dep[y]==dep[x]+1 ) {
            int t = dfs(y,min(flow,f));
            flow -= t;
            sum += t;
            e[i].f -= t;
            e[i^1].f += t;
        }
    }
    if ( sum==0 ) {
        dep[x] = 0;
    }
    return sum;
}

int dinic()
{
    int ans = 0;
    while ( bfs(s) ) {
        ans += dfs(s,0x3f3f3f3f);
    }
    return ans;
}

int main()
{
    //ios::sync_with_stdio(0);
    int i,j,k;
    scanf("%d %d",&student,&problem);
    for ( i=1;i<=student; i++ ) {
        scanf("%d",&solve[i]);
    }
    for ( i=1;i<=student; i++ ) {
        cin >> name[i];
    }
    for ( i=1; i<=student; i++ ) {
        for ( j=1; j<=problem; j++ ) {
            scanf("%1d",&a[i][j]);
        }
    }
    int maxx = -125;
    int Ans[3];
    for ( i=1; i<=student; i++ ) {
        for ( j=i+1; j<=student; j++ ) {
            for ( k=j+1; k<=student; k++ ) {
                s = 0; cnt = 0; t = 15;
                memset(head,-1,sizeof(head));
                memset(now,0,sizeof(now));
                addage(s,1,solve[i]);
                addage(s,2,solve[j]);
                addage(s,3,solve[k]);
                for ( int ii=1; ii<=problem; ii++ ) {
                    int tem = 0;
                    if ( a[i][ii]==1 ) {
                        tem += 1;
                    }
                    if ( a[j][ii]==1 ) {
                        tem += 2;
                    }
                    if ( a[k][ii]==1 ) {
                        tem += 4;
                    }
                    now[tem] ++;  //枚举每个问题有多少人能做，用上面的方法进行存储
                }

                for ( int man=1; man<=3; man++ ) {  //将人和集合连边
                    for ( int ii=1; ii<=7; ii++ ) {
                        if ( man==1 && (ii==1||ii==3||ii==5||ii==7) ) {
                            addage(man,3+ii,now[ii]);
                        }
                        if ( man==2 && (ii==2||ii==3||ii==6||ii==7) ) {
                            addage(man,3+ii,now[ii]);
                        }
                        if ( man==3 && (ii==4||ii==5||ii==6||ii==7) ) {
                            addage(man,3+ii,now[ii]);
                        }
                    }
                }

                for ( int ii=1; ii<=7; ii++ ) { //集合和超级汇点连边
                    addage(ii+3,t,now[ii]);
                }
                int now = dinic();
                if ( now>maxx ) {
                    maxx = now;
                    Ans[0] = i;
                    Ans[1] = j;
                    Ans[2] = k;
                }
            }
        }
    }
    printf("%d\n",maxx);
    cout << name[Ans[0]] << " "<<name[Ans[1]] << " "<<name[Ans[2]] << endl;


    return 0;
}

九羽-

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
（图论专题）【网络最大流】

（图论专题）【网络最大流】推荐视频：https://www.bilibili.com/video/av65039892?from=search&seid=1822150581423158194推荐阅读：https://blog.csdn.net/stevensonson/article/details/79177530网络流图是一张只有一个源点和汇点的有向图，而...
复制链接

扫一扫