5G全流程详解5：Polar译码

weixin_43831432

已于 2025-03-17 11:19:09 修改

阅读量202

点赞数 6

分类专栏：无线知识文章标签： 5G

于 2025-03-14 15:42:44 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_43831432/article/details/146199977

版权

无线知识专栏收录该内容

8 篇文章

订阅专栏

LR译码

LR是likelihood ratio的缩写。由于编码矩阵是二元域矩阵，那么我们有 ${H}'=H$ ，所以完全可以理解为译码为编码的逆过程。那么可以得到当编码输入数据长度为2时，译码过程如下图所示

$LR(\hat{a})$ 推导过程如下：

$p(\hat{a}=0)=p(\hat{c}=0)p(\hat{d}=0)+p(\hat{c}=1)p(\hat{d}=1)$

$p(\hat{a}=0)=p(\hat{c}=0)p(\hat{d}=1)+p(\hat{c}=1)p(\hat{d}=0)$

$LR(\hat{a})=\frac{p(\hat{a}=0)}{p(\hat{a}=1)}=\frac{p(\hat{c}=0)p(\hat{d}=0)+p(\hat{c}=1)p(\hat{d}=1)}{p(\hat{c}=0)p(\hat{d}=1)+p(\hat{c}=1)p(\hat{d}=0)}=\frac{1+\frac{p(\hat{c}=0)p(\hat{d}=0)}{p(\hat{c}=1)p(\hat{d}=1)}}{\frac{p(\hat{c}=0)}{p(\hat{c}=1)}+\frac{p(\hat{d}=0)}{p(\hat{d}=1)}}=\frac{1+LR(\hat{c})LR(\hat{d})}{LR(\hat{c})+LR(\hat{d})}$

$LR(\hat{b})$ 推导过程如下：

if $\hat{a}=0$

$P_{\hat{a}=0}(\hat{b}=0)=P(\hat{c}=0)P(\hat{d}=0)$

$P_{\hat{a}=0}(\hat{b}=1)=P(\hat{c}=1)P(\hat{d}=1)$

$LR_{\hat{a}=0}(\hat{b})=LR(\hat{c})LR(\hat{d})$

if $\hat{a}=1$

$P_{\hat{a}=1}(\hat{b}=0)=P(\hat{c}=1)P(\hat{d}=0)$

$P_{\hat{a}=1}(\hat{b}=1)=P(\hat{c}=0)P(\hat{d}=1)$

$LR_{\hat{a}=1}(\hat{b})=[LR(\hat{c})]^{-1}LR(\hat{d})$

所以可以得到

$LR(\hat{b})=[LR(\hat{c})]^{1-2\hat{a}}LR(\hat{d})$

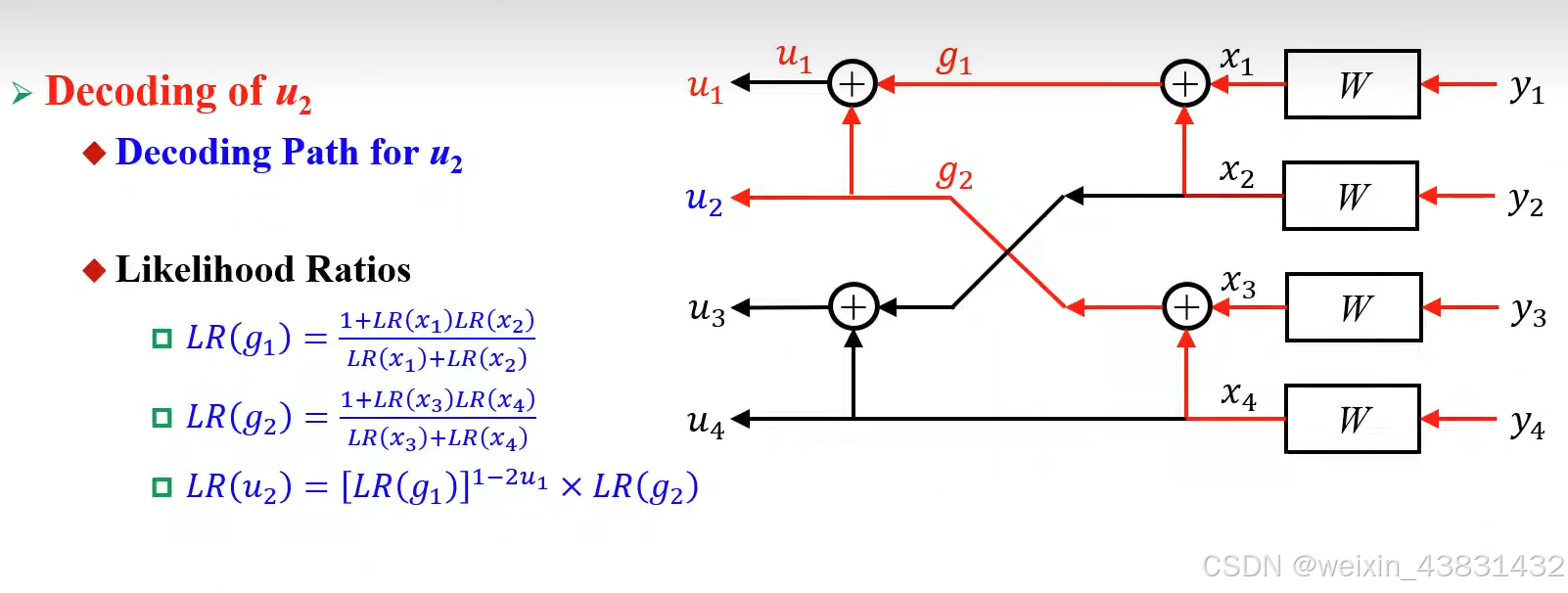
同理，当编码输入长度为4时，译码过程如下

进一步的，我们可以用二叉树的形式总结出极化码译码过程

我们可以看到，u1,u2,u3,u4的译码二叉树基本一致，除了输入u的不同。

我们可以引出g-node和f-node的概念

有u输入的，被称为g-node，没有u输入的，称为f-node。

那么如何确定每个节点有没有u输入以及u是多大呢？下面介绍一种利用生成矩阵产生u的方法

step 1

将M（前面译出的码元个数）写成二进制形式

$M=\sum _i2^i=2^{i_1}+2^{i_2}+...+2^{i_k}=M_1+M_2+...+M_k$

i表示被分配bit节点所在层数

step 2

将已解码bit向量 $u_{1}^{M}$ 分成子向量 $\bar{v}_1,\bar{v}_2,...,\bar{v}_k$ ，包含 $M_1,M_2,...,M_k$ 个bit，如下图所示

step 3

按下面公式计算在第 $i_1,i_2,...,i_k$ 层的node bits，G为生成矩阵

step 4

将node bits分配到相应节点，然后开始译码

下面举个例子来说明

当极化码code word长度N=8时，假设我们现在前5bit为[1 0 1 1 1]，我们现在要译码第六个bit，我们开始尝试用上面方法来完成译码：

step 1

$5=\sum _i2^i=2^{0}+2^{2}$

step 2

$\bar{v}_0$ 为u5， $\bar{v}_2$ 为[u1,u2,u3,u4]

step3

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。