Copula理论学习（三）--copula理论及参数copula函数族

在本书中，相关性的非正式表达与一个copula一致，即一个边缘分布为标准均匀分布的二元随机变量分布函数。（X1，X2）和（Y1，Y2）的copula便是（F1（X1），F2（X2））和（G1(Y1), G2(Y2)）的分布函数。（X1，X2）和（Y1，Y2）有相同的相关性可以表述为：（X1，X2）和（Y1，Y2）有相同的copula。
在上述的推理中，二元随机变量的边缘分布是已知的，但是在实际中，这样的假设是不合理的，多种类似的转换都会被用到。当两个数据集通过转换为标准正态分布的“标准化”计算后，可以得到与转换为标准均匀分布一样的结论。
因此，无论边际分布被转换为何种连续的单变量边际分布，都并不会改变copula方法研究相关性的核心。而由于概率和分位数转换，将边际分布转换为U（0,1）被证明是最方便的选择。

近年来，copula被广泛应用到定量风险管理，经济模型，或者环境模型中。“copula 狂热”主要立足于Sklar定理。

• Copula 定义和特征

一个d维的随机变量X（X1，…, Xd）的分布函数可以定义为：

• 例1：独立copula函数

公式为：

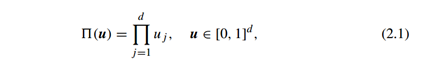
随机变量U的组成部分边缘分布均为U（0,1）通过R语言计算二维（d=2）的随机变量的独立copula结果为：

```r
####independent copula
library(copula)
d<-2 #设置变量的维度
ic<-indepCopula(dim=d)#先设置独立copula函数
set.seed(2008)#定义一个随机数种子
u<-runif(d)#生成一个二维的服从均匀分布的随机点
(Pi<-pCopula(u,copula=ic))#进行独立copula的计算
stopifnot(all.equal(Pi,prod(u)))#prod returns the product of all the values present in its arguments.
#all.equal 检查numerical equality of the sample
wireframe2(ic,FUN=pCopula,col4.=adjustcolor("black",alpha.f = 0.25)) # 画二维的表面图
contourplot2(ic,FUN=pCopula) #画等值线图

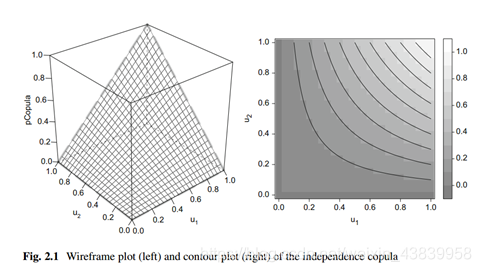从框线图中可以看出，独立copula在所有边缘上都是零，且П(u1,1)=u1,П(1,u2)=u2 对于所有的u1,u2属于[0,1]都成立。这两个特征在图中都标明了。事实上，任何d（d>=2）维的copula C 都有边界且拥有标准的均匀边缘分布，基于此原因，默认的wireframe2 画的图在视觉上强调了四个边缘线。
需要注意的是，仅仅是有边界和拥有标准均匀边际分布对于copula函数来说还不够。
为了令function C 成为一个copula，需要一个额外的特征来保证C是一个多维的分布函数df. 为了引进这个特征，我们需要额外的定义。
对于任意[0,1]d 范围内的a,b, a<=b, 令（a,b] 表示一个超矩形，则，对于任何[0,1]d 范围内的超矩形，定义其C-volume为：

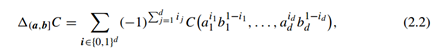
如果所有超矩形（a,b]的C-volume是非负的，则：

C成为d-increasing.
注意C-volume有一个自然的解释。对于U~C, 它可以被证实：

当d=2时，原表达式2.2变为：

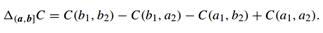
令C=П，我们来验证：一方面， =b1b2-b1a2-a1b2+a1a2=(b1-a1)(b2-a2)
另一方面，P（U€（a,b]）=P(a1<U1<b1) P(a2<U2<=b2)=(b1-a1)(b2-a2)

• 例2：C-volumes*

以下展示R中计算 a=(1/4,1/2) b=(1/3,1)的结果：

####C-volume方法1
a<-c(1/4,1/2)
b<-c(1/3,1)
stopifnot(0<=a,a<=1,0<=b,b<=1,a<=b)
p<-(b[1]-a[1])*(b[2]-a[2])
stopifnot(all.equal(prob(ic,l=a,u=b),p))
##方法2
n<-1000
set.seed(271)
U<-rCopula(n,copula=ic)#rcopula generates independent observations from a given copula
plot(U,xlab=quote(U[1]),ylab=quote(U[2]))
set.seed(271)
stopifnot(all.equal(U,matrix(runif(n*d),nrow=n)))
set.seed(314)
U<-rCopula(1e6,copul=ic)
p.sim<-mean(a[1]<U[,1]&U[,1]<=b[1]&a[2]<U[,2]&U[,2]<=b[2])
stopifnot(all.equal(p.sim,p,tol=1e-2))

如果一个copula C 存在密度，则其被称为绝对连续。在本书中，出于实际应用的目的，我们应该简要地称copula C 存在密度，如果

存在并且可积。dCopula()可用来计算copula密度。对于函数C：[0,1]d→[0,1] 来说，c对于所有的u都是非负的，并且C是d-increasing。这是因为任何C-volume
(即，U~C 落入到（a,b]中的概率)都能被表达为c 在（a,b]上的积分。
同样道理，参数化单变量分布对于单变量统计来说非常重要，参数化copula族在copula应用上扮演了重要的作用。下面介绍一些参数化copula族。

• 例3 Frank copula

####Frank copula
d<- 2 #dimension
theta<- -9 #copula parameter
fc<- frankCopula(theta,dim=d) # define a frank copula
set.seed(2010)
n<-5#number of evaluation points
u<- matrix(runif(n*d),nrow=n)#n random points in [0,1]^d
pCopula(u,copula=fc)# copula values at u
dCopula(u,copula=fc)#density values at u
wireframe2(fc,FUN=pCopula,draw.4.pCopula=FALSE)#wireframe plot copula
wireframe2(fc,FUN=dCopula,delta=0.001)#wireframe plot density
contourplot2(fc,FUN=pCopula)#contour plot(copula)
contourplot2(fc,FUN=dCopula,n.grid=72,lwd=1/2)#contour plot (density)

###
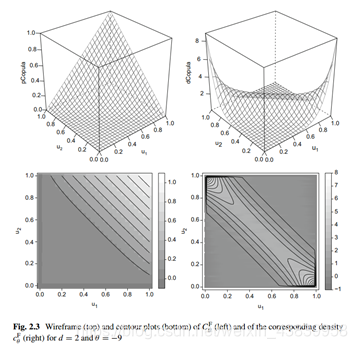
set.seed(1946)
n<-1000
U<-rCopula(n,copula=fc)#rcopula 用来产生服从frankcopula，参数分别为-9,0,9的1000个独立的值
U0<-rCopula(n,copula=setTheta(fc,value=0))#setTheta()用来改变Frank copula的参数
U9<-rCopula(n,copula=setTheta(fc,value=9))
plot(U,xlab=quote(U[1]),ylab=quote(U[2]))
plot(U0,xlab=quote(U[1]),ylab=quote(U[2]))
plot(U9,xlab=quote(U[1]),ylab=quote(U[2]))

• 例4 Clayton copula

作为参数化copula函数族另一个例子，Clayton函数族。对于d=2, 其公式为：

##########clayton copula
d<-3#dimension
cc<-claytonCopula(4,dim=d)#define clayton copula
set.seed(2013)
n<-5
u<-matrix(runif(n*d),nrow=n)#random points in the unit hypercube
pCopula(u,copula=cc)#copula value at u
dCopula(u,copula=cc)#density value at u
set.seed(271)
U<-rCopula(1000,copula=cc)
splom2(U,cex=0.3,col.mat="black")#scatter plot matrix

• 例5 Gumbel-Hougaard Copula

#######Gumbel copula
gc<- gumbelCopula(3)#theta=3(note the default dim=2)
set.seed(1993)
U<-rCopula(1000,copula=gc)
plot(U,xlab=quote(U[1]),ylab=quote(U[2]))
wireframe2(gc,dCopula,delta=0.025)

以上内容翻译自《Elements of copula modeling with R》