支持向量机问题引入
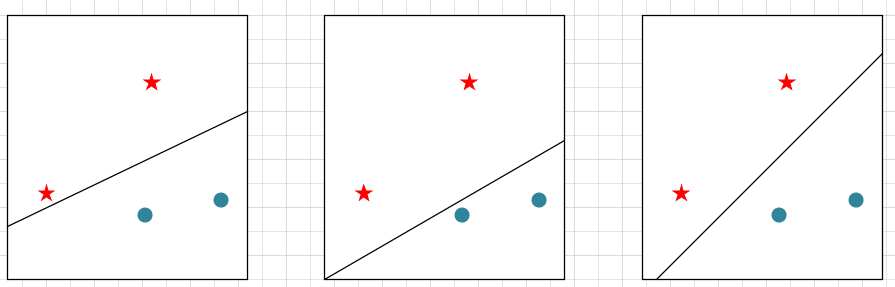
现有一个二分类问题,如上图所示,我们需要通过一条直线,将五角星和圆这两种类别分开,由图我们可以观察到,我们可以画任意1条线进行分割,都可以完成二分类的任务,但是可以看到第一张图的分割线对于五角星距离太近,当计算出现一些误差时,就有可能出现分类出错的情况,同理,图二也一样,而图三的分割线就可以将五角星和圆圈分的很开。
通俗的来说,我们需要找到一条分割线使得尽可能开的将五角星与圆圈分开。
相关知识补充
我们想尽可能的将样本点分离开,那么在数学上的表达就是,样本点到线的距离越大,那么我们需要进行距离的求解。
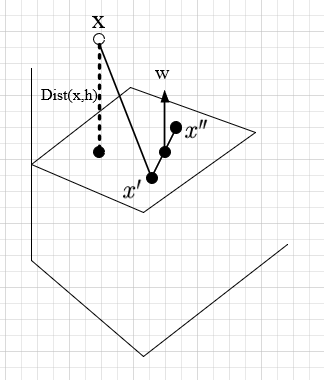
首先我们定义一个如上图所示的超平面,我们想求得x到超平面的距离,基本思路是,过点x做到平面的垂线,那么这条垂线的长度就是x到平面的距离,但是我们这样直接求难以得到结果,所以我们将问题转换。
我们将超平面表示为:
w
T
x
′
+
b
=
0
,
由于
x
′
与
x
′
′
都在超平面上,所以满足:
w
T
x
′
+
b
=
0
,
w
T
x
′
′
+
b
=
0
∴
w
T
x
′
=
−
b
,
w
T
x
′
′
=
−
b
∵
w
⊥
超平面
∵
w
T
⋅
(
x
′
′
−
x
′
)
=
0
,
其中
x
′
′
−
x
′
表示超平面上的向量
x
到平面的距离转换为:
x
−
x
′
向量做与法向量方向一致的映射便能得到
x
到平面的垂直距离
d
i
s
tan
c
e
(
x
,
b
,
w
)
=
∣
w
T
∣
∣
w
∣
∣
(
x
−
x
′
)
∣
p
s
:
w
T
∣
∣
w
∣
∣
表示法向量的单位方向
∵
w
T
x
′
=
−
b
∴
x
′
=
−
b
(
w
T
)
−
1
,
代入
d
i
s
tan
c
e
得:
d
i
s
tan
c
e
(
x
,
b
,
w
)
=
∣
w
T
∣
∣
w
∣
∣
(
x
+
b
(
w
T
)
−
1
)
∣
=
1
∣
∣
w
∣
∣
∣
(
w
T
x
+
b
)
∣
我们进行假设:
我们一共有
n
个样本点,分别表示为:
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
⋯
(
x
n
,
y
n
)
y
(
x
)
=
w
T
Φ
(
x
)
+
b
,
其中
Φ
(
x
)
表示样本点
Y
为样本类别:
当
X
为正例的时候
Y
=
+
1
,
y
(
x
i
)
>
0
⇔
y
i
=
+
1
当
X
为负例的时候
Y
=
−
1
,
y
(
x
i
)
<
0
⇔
y
i
=
−
1
可推出:
y
i
⋅
y
(
x
i
)
>
0
O
b
j
e
c
t
:
找到一条直线,使得离该线最近的点能够离这条线最远
(
核心
)
用数学公式表达
(
找到一对
w
,
b
,使得
a
r
g
max
(
w
,
b
)
得到
min
(
d
i
c
tan
c
e
)
)
d
i
s
tan
c
e
(
x
,
b
,
w
)
=
1
∣
∣
w
∣
∣
∣
(
w
T
x
+
b
)
∣
∵
y
i
⋅
y
(
x
i
)
>
0
,
y
(
x
)
=
w
T
Φ
(
x
i
)
+
b
,
y
i
=
±
1
∴
y
i
(
w
T
Φ
(
x
i
)
+
b
)
>
0
∴
我们利用
y
i
来去掉绝对值
∴
d
i
s
tan
c
e
(
x
,
b
,
w
)
=
1
∣
∣
w
∣
∣
∣
(
w
T
x
+
b
)
∣
=
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
∥
w
∥
∴
O
b
j
e
c
t
f
u
n
c
t
i
o
n
=
a
r
g
max
w
,
b
{
1
∥
w
∥
min
i
[
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
]
}
为了计算简便,我们将
y
i
(
w
T
Φ
(
x
)
+
b
)
>
0
左右两边同时进行放缩,使得不等式成立,即:
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
,
那么显而易见,
min
i
[
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
]
=
1
∴
O
b
j
e
c
t
f
u
n
c
t
i
o
n
=
a
r
g
max
w
,
b
1
∥
w
∥
∵
在机器学习中,我们擅长求极小值,而不是极大值
∴
O
b
j
e
c
t
f
u
n
c
t
i
o
n
=
a
r
g
max
w
,
b
1
∥
w
∥
且
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
可以转换成:
O
b
j
e
c
t
f
u
n
c
t
i
o
n
=
min
w
,
b
1
2
w
2
且
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
(
系数
1
2
方便求导操作,
w
2
用来去绝对值
)
∵
我们得到的目标函数需要求
min
w
,
b
1
2
w
2
并且同时需要满足
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
这个条件
∴
我们不能直接进行求导操作
此时我们想到拉格朗日乘子法,其标准格式为:
min
f
(
x
)
s
.
t
.
g
i
(
x
)
≤
0
,
i
=
1
,
.
.
.
,
m
(
约束条件
)
与上式相符
∵
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
∴
1
−
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≤
0
我们将超平面表示为:
w
T
x
′
+
b
=
0
,
由于
x
′
与
x
′
′
都在超平面上,所以满足:
w
T
x
′
+
b
=
0
,
w
T
x
′
′
+
b
=
0
∴
w
T
x
′
=
−
b
,
w
T
x
′
′
=
−
b
∵
w
⊥
超平面
∵
w
T
⋅
(
x
′
′
−
x
′
)
=
0
,
其中
x
′
′
−
x
′
表示超平面上的向量
x
到平面的距离转换为:
x
−
x
′
向量做与法向量方向一致的映射便能得到
x
到平面的垂直距离
d
i
s
tan
c
e
(
x
,
b
,
w
)
=
∣
w
T
∣
∣
w
∣
∣
(
x
−
x
′
)
∣
p
s
:
w
T
∣
∣
w
∣
∣
表示法向量的单位方向
∵
w
T
x
′
=
−
b
∴
x
′
=
−
b
(
w
T
)
−
1
,
代入
d
i
s
tan
c
e
得:
d
i
s
tan
c
e
(
x
,
b
,
w
)
=
∣
w
T
∣
∣
w
∣
∣
(
x
+
b
(
w
T
)
−
1
)
∣
=
1
∣
∣
w
∣
∣
∣
(
w
T
x
+
b
)
∣
我们进行假设:
我们一共有
n
个样本点,分别表示为:
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
⋯
(
x
n
,
y
n
)
y
(
x
)
=
w
T
Φ
(
x
)
+
b
,
其中
Φ
(
x
)
表示样本点
Y
为样本类别:
当
X
为正例的时候
Y
=
+
1
,
y
(
x
i
)
>
0
⇔
y
i
=
+
1
当
X
为负例的时候
Y
=
−
1
,
y
(
x
i
)
<
0
⇔
y
i
=
−
1
可推出:
y
i
⋅
y
(
x
i
)
>
0
O
b
j
e
c
t
:
找到一条直线,使得离该线最近的点能够离这条线最远
(
核心
)
用数学公式表达
(
找到一对
w
,
b
,使得
a
r
g
max
(
w
,
b
)
得到
min
(
d
i
c
tan
c
e
)
)
d
i
s
tan
c
e
(
x
,
b
,
w
)
=
1
∣
∣
w
∣
∣
∣
(
w
T
x
+
b
)
∣
∵
y
i
⋅
y
(
x
i
)
>
0
,
y
(
x
)
=
w
T
Φ
(
x
i
)
+
b
,
y
i
=
±
1
∴
y
i
(
w
T
Φ
(
x
i
)
+
b
)
>
0
∴
我们利用
y
i
来去掉绝对值
∴
d
i
s
tan
c
e
(
x
,
b
,
w
)
=
1
∣
∣
w
∣
∣
∣
(
w
T
x
+
b
)
∣
=
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
∥
w
∥
∴
O
b
j
e
c
t
f
u
n
c
t
i
o
n
=
a
r
g
max
w
,
b
{
1
∥
w
∥
min
i
[
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
]
}
为了计算简便,我们将
y
i
(
w
T
Φ
(
x
)
+
b
)
>
0
左右两边同时进行放缩,使得不等式成立,即:
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
,
那么显而易见,
min
i
[
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
]
=
1
∴
O
b
j
e
c
t
f
u
n
c
t
i
o
n
=
a
r
g
max
w
,
b
1
∥
w
∥
∵
在机器学习中,我们擅长求极小值,而不是极大值
∴
O
b
j
e
c
t
f
u
n
c
t
i
o
n
=
a
r
g
max
w
,
b
1
∥
w
∥
且
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
可以转换成:
O
b
j
e
c
t
f
u
n
c
t
i
o
n
=
min
w
,
b
1
2
w
2
且
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
(
系数
1
2
方便求导操作,
w
2
用来去绝对值
)
∵
我们得到的目标函数需要求
min
w
,
b
1
2
w
2
并且同时需要满足
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
这个条件
∴
我们不能直接进行求导操作
此时我们想到拉格朗日乘子法,其标准格式为:
min
f
(
x
)
s
.
t
.
g
i
(
x
)
≤
0
,
i
=
1
,
.
.
.
,
m
(
约束条件
)
与上式相符
∵
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≥
1
∴
1
−
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
≤
0
∴
f
(
x
)
=
1
2
w
2
,
g
i
(
x
)
=
1
−
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
,
i
=
1
,
.
.
.
,
m
∵
L
(
α
)
=
f
(
x
)
+
α
g
i
(
x
)
(
拉格朗日乘子法公式
)
∴
L
(
w
,
b
,
α
)
=
1
2
w
2
−
∑
i
=
1
n
α
i
(
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
−
1
)
min
f
(
x
)
=
min
w
,
b
max
α
L
(
w
,
b
,
α
)
(
找到一个
α
使得
L
(
α
)
最大,进而使得
L
(
w
,
b
,
α
)
实现我们的目标
)
∵
我们擅长求极小值,而不是极大值
∴
我们利用拉格朗日乘子法的对偶问题:
min
w
,
b
max
α
L
(
w
,
b
,
α
)
⇒
max
α
min
w
,
b
L
(
w
,
b
,
α
)
(
求最大值里的最小的一个一定比最小值里最大的一个要大
)
分别对
w
,
b
求偏导得:
∂
L
∂
w
=
w
−
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
=
0
⇒
w
=
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
∂
L
∂
b
=
∑
i
=
1
n
α
i
y
i
=
0
把
w
=
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
,
∑
i
=
1
n
α
i
y
i
=
0
带入下式得:
L
(
w
,
b
,
α
)
=
1
2
w
2
−
∑
i
=
1
n
α
i
(
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
−
1
)
=
1
2
∥
w
∥
2
−
∑
i
=
1
n
α
i
(
y
i
⋅
(
w
T
⋅
Φ
(
x
i
)
+
b
)
−
1
)
=
1
2
w
T
w
−
w
T
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
−
b
∑
i
=
1
n
α
i
y
i
+
∑
i
=
1
n
α
i
=
1
2
(
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
)
T
(
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
)
−
(
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
)
T
(
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
)
+
∑
i
=
1
n
α
i
=
∑
i
=
1
n
α
i
−
1
2
(
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
)
T
(
∑
i
=
1
n
α
i
y
i
Φ
(
x
i
)
)
=
∑
i
=
1
n
α
i
−
1
2
∑
i
=
1
,
j
=
1
n
α
i
α
j
y
i
y
j
Φ
T
(
x
i
)
Φ
(
x
j
)
∴
min
w
,
b
L
(
w
,
b
,
α
)
=
∑
i
=
1
n
α
i
−
1
2
∑
i
=
1
,
j
=
1
n
α
i
α
j
y
i
y
j
Φ
T
(
x
i
)
Φ
(
x
j
)
接着求:
max
α
L
(
α
)
=
∑
i
=
1
n
α
i
−
1
2
∑
i
=
1
,
j
=
1
n
α
i
α
j
y
i
y
j
Φ
T
(
x
i
)
Φ
(
x
j
)
,且
∑
i
=
1
n
α
i
y
i
=
0
,
α
i
≥
0
∵
求一个数的最大值就是求一个数相反数的极小值
∴
max
α
L
(
α
)
=
∑
i
=
1
n
α
i
−
1
2
∑
i
=
1
,
j
=
1
n
α
i
α
j
y
i
y
j
Φ
T
(
x
i
)
Φ
(
x
j
)
⇒
min
α
L
(
α
)
=
1
2
∑
i
=
1
,
j
=
1
n
α
i
α
j
y
i
y
j
Φ
T
(
x
i
)
Φ
(
x
j
)
−
∑
i
=
1
n
α
i
,
且
∑
i
=
1
n
α
i
y
i
=
0
,
α
i
≥
0
.
\\ 我们将超平面表示为:w^Tx^{'}+b=0,\ \text{由于}x^{'}\text{与}x^{''}\text{都在超平面上,所以满足:}\\ \\ w^Tx^{'}+b=0\text{,}w^Tx^{''}+b=0\\ \\ \therefore w^Tx^{'}=-b,w^Tx^{''}=-b\\ \\ \because w\bot 超平面\\ ~\\ \because w^T\cdot \left( x^{''}-x^{'} \right) =0,\text{其中}x^{''}-x^{'}\text{表示超平面上的向量}\\ ~\\ x\text{到平面的距离转换为:}x-x^{'}\text{向量做与法向量方向一致的映射便能得到}x\text{到平面的垂直距离}\\ ~\\ dis\tan ce\left( x,b,w \right) =\left| \frac{w^T}{||w||}\left( x-x^{'} \right) \right|\\ ~\\ ps:\ \frac{w^T}{||w||}\text{表示法向量的单位方向}\\ ~\\ \because w^Tx^{'}=-b\\ ~\\ \therefore x^{'}=-b\left( w^T \right) ^{-1},\text{代入}dis\tan ce\text{得:}\\ ~\\ dis\tan ce\left( x,b,w \right) =\left| \frac{w^T}{||w||}\left( x+b\left( w^T \right) ^{-1} \right) \right|=\frac{1}{||w||}\left| \left( w^Tx+b \right) \right|\\ ~\\ \text{我们进行假设:}\\ ~\\ \text{我们一共有}n\text{个样本点,分别表示为:}\left( x_1,\ y_1 \right) ,\left( x_2,\,\,y_2 \right) \cdots \left( x_n,\,\,y_n \right) \\ ~\\ y\left( x \right) =w^T\varPhi \left( x \right) +b,\text{其中}\varPhi \left( x \right) \text{表示样本点}\\ ~\\ Y\text{为样本类别:}\\ ~\\ \text{当}X\text{为正例的时候}Y=+1,y\left( x_i \right) >0\Leftrightarrow y_i=+1\\ ~\\ \text{当}X\text{为负例的时候}Y=-1,y\left( x_i \right) <0\Leftrightarrow y_i=-1\\ ~\\ \text{可推出:}y_i\cdot y\left( x_i \right) >0\\ ~\\ Object:\ \text{找到一条直线,使得离该线最近的点能够离这条线最远}\left( \text{核心} \right) \\ ~\\ \text{用数学公式表达}\left( \text{找到一对}w,b\text{,使得}arg\max \left( w,b \right) \text{得到}\min \left( dic\tan ce \right) \right) \\ ~\\ dis\tan ce\left( x,b,w \right) =\frac{1}{||w||}\left| \left( w^Tx+b \right) \right|\\ ~\\ \because y_i\cdot y\left( x_i \right) >0,y\left( x \right) =w^T\varPhi \left( x_i \right) +b,y_i=\pm 1\\ ~\\ \therefore y_i\left( w^T\varPhi \left( x_i \right) +b \right) >0\\ ~\\ \therefore \text{我们利用}y_i\text{来去掉绝对值}\\ ~\\ \therefore dis\tan ce\left( x,b,w \right) =\frac{1}{||w||}\left| \left( w^Tx+b \right) \right|=\frac{y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right)}{\lVert w \rVert}\\ ~\\ \therefore Object\ function=\underset{w,b}{arg\max}\left\{ \frac{1}{\lVert w \rVert}\underset{i}{\min}\left[ y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \right] \right\} \\ ~\\ \text{为了计算简便,我们将}y_i\left( w^T\varPhi \left( x \right) +b \right) >0\text{左右两边同时进行放缩,使得不等式成立,即:}\\ ~\\ y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1,\text{那么显而易见,}\underset{i}{\min}\left[ y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \right] =1\\ ~\\ \therefore Object\,\,function=\underset{w,b}{arg\max}\frac{1}{\lVert w \rVert}\\ ~\\ \because \text{在机器学习中,我们擅长求极小值,而不是极大值}\\ ~\\ \therefore Object\,\,function=\underset{w,b}{arg\max}\frac{1}{\lVert w \rVert}\ \text{且}y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1\text{可以转换成:}\\ ~\\ Object\,\,function=\underset{w,b}{\min}\sqrt{\frac{1}{2}w^2}\,\,\text{且}y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1\ \ \ \left( \text{系数}\frac{1}{2}\text{方便求导操作,}w^2\text{用来去绝对值} \right) \\ ~\\ \because \text{我们得到的目标函数需要求}\underset{w,b}{\min}\frac{1}{2}w^2\text{并且同时需要满足}y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1\,\,\text{这个条件}\\ ~\\ \therefore \text{我们不能直接进行求导操作}\\ ~\\ \text{此时我们想到拉格朗日乘子法,其标准格式为:}\\ ~\\ \min\text{\ }f\left( x \right) \\ ~\\ s.t.\ g_i\left( x \right) \le 0,\ \ \ \ \ i=1,...,m\ \left( \text{约束条件} \right) \ \text{与上式相符}\\ ~\\ \because y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1\,\,\,\,\\ ~\\ \therefore 1-y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \le 0\\ ~\\ 我们将超平面表示为:w^Tx^{'}+b=0,\ \text{由于}x^{'}\text{与}x^{''}\text{都在超平面上,所以满足:}\\ ~\\ w^Tx^{'}+b=0\text{,}w^Tx^{''}+b=0\\ ~\\ \therefore w^Tx^{'}=-b,w^Tx^{''}=-b\\ ~\\ \because w\bot 超平面\\ ~\\ \because w^T\cdot \left( x^{''}-x^{'} \right) =0,\text{其中}x^{''}-x^{'}\text{表示超平面上的向量}\\ ~\\ x\text{到平面的距离转换为:}x-x^{'}\text{向量做与法向量方向一致的映射便能得到}x\text{到平面的垂直距离}\\ ~\\ dis\tan ce\left( x,b,w \right) =\left| \frac{w^T}{||w||}\left( x-x^{'} \right) \right|\\ ~\\ ps:\ \frac{w^T}{||w||}\text{表示法向量的单位方向}\\ ~\\ \because w^Tx^{'}=-b\\ ~\\ \therefore x^{'}=-b\left( w^T \right) ^{-1},\text{代入}dis\tan ce\text{得:}\\ ~\\ dis\tan ce\left( x,b,w \right) =\left| \frac{w^T}{||w||}\left( x+b\left( w^T \right) ^{-1} \right) \right|=\frac{1}{||w||}\left| \left( w^Tx+b \right) \right|\\ ~\\ \text{我们进行假设:}\\ ~\\ \text{我们一共有}n\text{个样本点,分别表示为:}\left( x_1,\ y_1 \right) ,\left( x_2,\,\,y_2 \right) \cdots \left( x_n,\,\,y_n \right) \\ ~\\ y\left( x \right) =w^T\varPhi \left( x \right) +b,\text{其中}\varPhi \left( x \right) \text{表示样本点}\\ ~\\ Y\text{为样本类别:}\\ ~\\ \text{当}X\text{为正例的时候}Y=+1,y\left( x_i \right) >0\Leftrightarrow y_i=+1\\ ~\\ \text{当}X\text{为负例的时候}Y=-1,y\left( x_i \right) <0\Leftrightarrow y_i=-1\\ ~\\ \text{可推出:}y_i\cdot y\left( x_i \right) >0\\ ~\\ Object:\ \text{找到一条直线,使得离该线最近的点能够离这条线最远}\left( \text{核心} \right) \\ ~\\ \text{用数学公式表达}\left( \text{找到一对}w,b\text{,使得}arg\max \left( w,b \right) \text{得到}\min \left( dic\tan ce \right) \right) \\ ~\\ dis\tan ce\left( x,b,w \right) =\frac{1}{||w||}\left| \left( w^Tx+b \right) \right|\\ ~\\ \because y_i\cdot y\left( x_i \right) >0,y\left( x \right) =w^T\varPhi \left( x_i \right) +b,y_i=\pm 1\\ ~\\ \therefore y_i\left( w^T\varPhi \left( x_i \right) +b \right) >0\\ ~\\ \therefore \text{我们利用}y_i\text{来去掉绝对值}\\ ~\\ \therefore dis\tan ce\left( x,b,w \right) =\frac{1}{||w||}\left| \left( w^Tx+b \right) \right|=\frac{y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right)}{\lVert w \rVert}\\ ~\\ \therefore Object\ function=\underset{w,b}{arg\max}\left\{ \frac{1}{\lVert w \rVert}\underset{i}{\min}\left[ y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \right] \right\} \\ ~\\ \text{为了计算简便,我们将}y_i\left( w^T\varPhi \left( x \right) +b \right) >0\text{左右两边同时进行放缩,使得不等式成立,即:}\\ ~\\ y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1,\text{那么显而易见,}\underset{i}{\min}\left[ y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \right] =1\\ ~\\ \therefore Object\,\,function=\underset{w,b}{arg\max}\frac{1}{\lVert w \rVert}\\ ~\\ \because \text{在机器学习中,我们擅长求极小值,而不是极大值}\\ ~\\ \therefore Object\,\,function=\underset{w,b}{arg\max}\frac{1}{\lVert w \rVert}\ \text{且}y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1\text{可以转换成:}\\ ~\\ Object\,\,function=\underset{w,b}{\min}\frac{1}{2}w^2\,\,\text{且}y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1\ \ \ \left( \text{系数}\frac{1}{2}\text{方便求导操作,}w^2\text{用来去绝对值} \right) \\ ~\\ \because \text{我们得到的目标函数需要求}\underset{w,b}{\min}\frac{1}{2}w^2\text{并且同时需要满足}y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1\,\,\text{这个条件}\\ ~\\ \therefore \text{我们不能直接进行求导操作}\\ ~\\ \text{此时我们想到拉格朗日乘子法,其标准格式为:}\\ ~\\ \min\text{\ }f\left( x \right) \\ ~\\ s.t.\ g_i\left( x \right) \le 0,\ \ \ \ \ i=1,...,m\ \left( \text{约束条件} \right) \ \text{与上式相符}\\ ~\\ \because y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ge 1\,\,\,\,\\ ~\\ \therefore 1-y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \le 0\\ ~\\ \therefore f\left( x \right) =\frac{1}{2}w^2,\ g_i\left( x \right) =1-y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) \ ,\,\,\,\,\,\,\,\,\,\,i=1,...,m\\ ~\\ \because L\left( \alpha \right) =f\left( x \right) +\alpha \,\,g_i\left( x \right) \ \left( \text{拉格朗日乘子法公式} \right) \\ ~\\ \therefore L\left( w,b,\alpha \right) =\frac{1}{2}w^2-\sum_{i=1}^n{\alpha _i\left( y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) -1 \right)}\\ ~\\ \min\text{\,\,}f\left( x \right) =\underset{w,b}{\min}\underset{\alpha}{\max}L\left( w,b,\alpha \right) \left( \text{找到一个}\alpha \text{使得}L\left( \alpha \right) \text{最大,进而使得}L\left( w,b,\alpha \right) \text{实现我们的目标} \right) \\ ~\\ \because \text{我们擅长求极小值,而不是极大值}\\ ~\\ \therefore \text{我们利用拉格朗日乘子法的对偶问题:}\\ ~\\ \underset{w,b}{\min}\underset{\alpha}{\max}L\left( w,b,\alpha \right) \Rightarrow \underset{\alpha}{\max}\underset{w,b}{\min}L\left( w,b,\alpha \right) \left( \text{求最大值里的最小的一个一定比最小值里最大的一个要大} \right) \\ ~\\ \text{分别对}w,b\text{求偏导得:}\\ ~\\ \frac{\partial L}{\partial w}=w-\sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)}=0\Rightarrow w=\sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)}\\ ~\\ \frac{\partial L}{\partial b}=\sum_{i=1}^n{\alpha _iy_i}=0\\ ~\\ \text{把}w=\sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)}\text{,}\sum_{i=1}^n{\alpha _iy_i}=0\text{带入下式得:\ }\\ ~\\ L\left( w,b,\alpha \right) =\frac{1}{2}w^2-\sum_{i=1}^n{\alpha _i\left( y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) -1 \right)}\\ ~\\ =\frac{1}{2}\lVert w \rVert ^2-\sum_{i=1}^n{\alpha _i\left( y_i\cdot \left( w^T\cdot \varPhi \left( x_i \right) +b \right) -1 \right)}\\ ~\\ =\frac{1}{2}w^Tw-w^T\sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right) -b}\sum_{i=1}^n{\alpha _iy_i}+\sum_{i=1}^n{\alpha _i}\\ ~\\ =\frac{1}{2}\left( \sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)} \right) ^T\left( \sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)} \right) -\left( \sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)} \right) ^T\left( \sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)} \right) +\sum_{i=1}^n{\alpha _i}\\ ~\\ =\sum_{i=1}^n{\alpha _i}-\frac{1}{2}\left( \sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)} \right) ^T\left( \sum_{i=1}^n{\alpha _iy_i\varPhi \left( x_i \right)} \right) \\ ~\\ =\sum_{i=1}^n{\alpha _i}-\frac{1}{2}\sum_{i=1,j=1}^n{\alpha _i\alpha _jy_iy_j\varPhi ^T\left( x_i \right) \varPhi \left( x_j \right)}\\ ~\\ \therefore \underset{w,b}{\min}L\left( w,b,\alpha \right) =\sum_{i=1}^n{\alpha _i}-\frac{1}{2}\sum_{i=1,j=1}^n{\alpha _i\alpha _jy_iy_j\varPhi ^T\left( x_i \right) \varPhi \left( x_j \right)}\ \\ ~\\ \text{接着求:}\\ ~\\ \underset{\alpha}{\max}L\left( \alpha \right) =\sum_{i=1}^n{\alpha _i}-\frac{1}{2}\sum_{i=1,j=1}^n{\alpha _i\alpha _jy_iy_j\varPhi ^T\left( x_i \right) \varPhi \left( x_j \right)}\text{,且}\sum_{i=1}^n{\alpha _iy_i}=0\text{,}\alpha _i\ge 0\\ ~\\ \because \text{求一个数的最大值就是求一个数相反数的极小值}\\ ~\\ \therefore \underset{\alpha}{\max}L\left( \alpha \right) =\sum_{i=1}^n{\alpha _i}-\frac{1}{2}\sum_{i=1,j=1}^n{\alpha _i\alpha _jy_iy_j\varPhi ^T\left( x_i \right) \varPhi \left( x_j \right)}\\ ~\\ \Rightarrow \underset{\alpha}{\min}L\left( \alpha \right) =\frac{1}{2}\sum_{i=1,j=1}^n{\alpha _i\alpha _jy_iy_j\varPhi ^T\left( x_i \right) \varPhi \left( x_j \right)}-\sum_{i=1}^n{\alpha _i},\text{且}\sum_{i=1}^n{\alpha _iy_i}=0\text{,}\alpha _i\ge 0\\ \\.
我们将超平面表示为:wTx′+b=0, 由于x′与x′′都在超平面上,所以满足:wTx′+b=0,wTx′′+b=0∴wTx′=−b,wTx′′=−b∵w⊥超平面 ∵wT⋅(x′′−x′)=0,其中x′′−x′表示超平面上的向量 x到平面的距离转换为:x−x′向量做与法向量方向一致的映射便能得到x到平面的垂直距离 distance(x,b,w)=
∣∣w∣∣wT(x−x′)
ps: ∣∣w∣∣wT表示法向量的单位方向 ∵wTx′=−b ∴x′=−b(wT)−1,代入distance得: distance(x,b,w)=
∣∣w∣∣wT(x+b(wT)−1)
=∣∣w∣∣1
(wTx+b)
我们进行假设: 我们一共有n个样本点,分别表示为:(x1, y1),(x2,y2)⋯(xn,yn) y(x)=wTΦ(x)+b,其中Φ(x)表示样本点 Y为样本类别: 当X为正例的时候Y=+1,y(xi)>0⇔yi=+1 当X为负例的时候Y=−1,y(xi)<0⇔yi=−1 可推出:yi⋅y(xi)>0 Object: 找到一条直线,使得离该线最近的点能够离这条线最远(核心) 用数学公式表达(找到一对w,b,使得argmax(w,b)得到min(dictance)) distance(x,b,w)=∣∣w∣∣1
(wTx+b)
∵yi⋅y(xi)>0,y(x)=wTΦ(xi)+b,yi=±1 ∴yi(wTΦ(xi)+b)>0 ∴我们利用yi来去掉绝对值 ∴distance(x,b,w)=∣∣w∣∣1
(wTx+b)
=∥w∥yi⋅(wT⋅Φ(xi)+b) ∴Object function=w,bargmax{∥w∥1imin[yi⋅(wT⋅Φ(xi)+b)]} 为了计算简便,我们将yi(wTΦ(x)+b)>0左右两边同时进行放缩,使得不等式成立,即: yi⋅(wT⋅Φ(xi)+b)≥1,那么显而易见,imin[yi⋅(wT⋅Φ(xi)+b)]=1 ∴Objectfunction=w,bargmax∥w∥1 ∵在机器学习中,我们擅长求极小值,而不是极大值 ∴Objectfunction=w,bargmax∥w∥1 且yi⋅(wT⋅Φ(xi)+b)≥1可以转换成: Objectfunction=w,bmin21w2且yi⋅(wT⋅Φ(xi)+b)≥1 (系数21方便求导操作,w2用来去绝对值) ∵我们得到的目标函数需要求w,bmin21w2并且同时需要满足yi⋅(wT⋅Φ(xi)+b)≥1这个条件 ∴我们不能直接进行求导操作 此时我们想到拉格朗日乘子法,其标准格式为: min f(x) s.t. gi(x)≤0, i=1,...,m (约束条件) 与上式相符 ∵yi⋅(wT⋅Φ(xi)+b)≥1 ∴1−yi⋅(wT⋅Φ(xi)+b)≤0 我们将超平面表示为:wTx′+b=0, 由于x′与x′′都在超平面上,所以满足: wTx′+b=0,wTx′′+b=0 ∴wTx′=−b,wTx′′=−b ∵w⊥超平面 ∵wT⋅(x′′−x′)=0,其中x′′−x′表示超平面上的向量 x到平面的距离转换为:x−x′向量做与法向量方向一致的映射便能得到x到平面的垂直距离 distance(x,b,w)=
∣∣w∣∣wT(x−x′)
ps: ∣∣w∣∣wT表示法向量的单位方向 ∵wTx′=−b ∴x′=−b(wT)−1,代入distance得: distance(x,b,w)=
∣∣w∣∣wT(x+b(wT)−1)
=∣∣w∣∣1
(wTx+b)
我们进行假设: 我们一共有n个样本点,分别表示为:(x1, y1),(x2,y2)⋯(xn,yn) y(x)=wTΦ(x)+b,其中Φ(x)表示样本点 Y为样本类别: 当X为正例的时候Y=+1,y(xi)>0⇔yi=+1 当X为负例的时候Y=−1,y(xi)<0⇔yi=−1 可推出:yi⋅y(xi)>0 Object: 找到一条直线,使得离该线最近的点能够离这条线最远(核心) 用数学公式表达(找到一对w,b,使得argmax(w,b)得到min(dictance)) distance(x,b,w)=∣∣w∣∣1
(wTx+b)
∵yi⋅y(xi)>0,y(x)=wTΦ(xi)+b,yi=±1 ∴yi(wTΦ(xi)+b)>0 ∴我们利用yi来去掉绝对值 ∴distance(x,b,w)=∣∣w∣∣1
(wTx+b)
=∥w∥yi⋅(wT⋅Φ(xi)+b) ∴Object function=w,bargmax{∥w∥1imin[yi⋅(wT⋅Φ(xi)+b)]} 为了计算简便,我们将yi(wTΦ(x)+b)>0左右两边同时进行放缩,使得不等式成立,即: yi⋅(wT⋅Φ(xi)+b)≥1,那么显而易见,imin[yi⋅(wT⋅Φ(xi)+b)]=1 ∴Objectfunction=w,bargmax∥w∥1 ∵在机器学习中,我们擅长求极小值,而不是极大值 ∴Objectfunction=w,bargmax∥w∥1 且yi⋅(wT⋅Φ(xi)+b)≥1可以转换成: Objectfunction=w,bmin21w2且yi⋅(wT⋅Φ(xi)+b)≥1 (系数21方便求导操作,w2用来去绝对值) ∵我们得到的目标函数需要求w,bmin21w2并且同时需要满足yi⋅(wT⋅Φ(xi)+b)≥1这个条件 ∴我们不能直接进行求导操作 此时我们想到拉格朗日乘子法,其标准格式为: min f(x) s.t. gi(x)≤0, i=1,...,m (约束条件) 与上式相符 ∵yi⋅(wT⋅Φ(xi)+b)≥1 ∴1−yi⋅(wT⋅Φ(xi)+b)≤0 ∴f(x)=21w2, gi(x)=1−yi⋅(wT⋅Φ(xi)+b) ,i=1,...,m ∵L(α)=f(x)+αgi(x) (拉格朗日乘子法公式) ∴L(w,b,α)=21w2−∑i=1nαi(yi⋅(wT⋅Φ(xi)+b)−1) minf(x)=w,bminαmaxL(w,b,α)(找到一个α使得L(α)最大,进而使得L(w,b,α)实现我们的目标) ∵我们擅长求极小值,而不是极大值 ∴我们利用拉格朗日乘子法的对偶问题: w,bminαmaxL(w,b,α)⇒αmaxw,bminL(w,b,α)(求最大值里的最小的一个一定比最小值里最大的一个要大) 分别对w,b求偏导得: ∂w∂L=w−∑i=1nαiyiΦ(xi)=0⇒w=∑i=1nαiyiΦ(xi) ∂b∂L=∑i=1nαiyi=0 把w=∑i=1nαiyiΦ(xi),∑i=1nαiyi=0带入下式得: L(w,b,α)=21w2−∑i=1nαi(yi⋅(wT⋅Φ(xi)+b)−1) =21∥w∥2−∑i=1nαi(yi⋅(wT⋅Φ(xi)+b)−1) =21wTw−wT∑i=1nαiyiΦ(xi)−b∑i=1nαiyi+∑i=1nαi =21(∑i=1nαiyiΦ(xi))T(∑i=1nαiyiΦ(xi))−(∑i=1nαiyiΦ(xi))T(∑i=1nαiyiΦ(xi))+∑i=1nαi =∑i=1nαi−21(∑i=1nαiyiΦ(xi))T(∑i=1nαiyiΦ(xi)) =∑i=1nαi−21∑i=1,j=1nαiαjyiyjΦT(xi)Φ(xj) ∴w,bminL(w,b,α)=∑i=1nαi−21∑i=1,j=1nαiαjyiyjΦT(xi)Φ(xj) 接着求: αmaxL(α)=∑i=1nαi−21∑i=1,j=1nαiαjyiyjΦT(xi)Φ(xj),且∑i=1nαiyi=0,αi≥0 ∵求一个数的最大值就是求一个数相反数的极小值 ∴αmaxL(α)=∑i=1nαi−21∑i=1,j=1nαiαjyiyjΦT(xi)Φ(xj) ⇒αminL(α)=21∑i=1,j=1nαiαjyiyjΦT(xi)Φ(xj)−∑i=1nαi,且∑i=1nαiyi=0,αi≥0.
例题引入:
如下图所示的训练数据集,其正例点是x1=(3,3), x2=(4,3),负例点是x3=(1,1),试求最大间隔分离超平面?
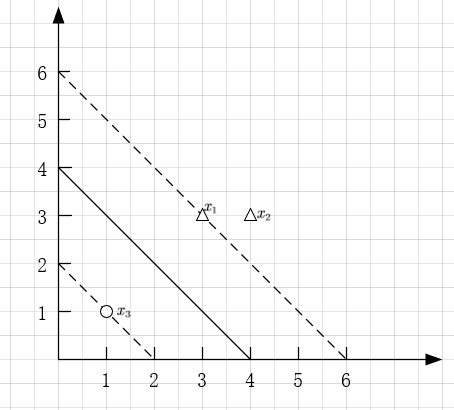
样本:
x
1
(
3
,
3
,
1
)
,
x
2
=
(
4
,
3
,
1
)
,
x
3
=
(
1
,
1
,
−
1
)
求解:
1
2
∑
i
=
1
n
∑
j
=
1
n
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
−
∑
i
=
1
n
α
i
,
且
α
1
+
α
2
−
α
3
=
0
,
α
i
≥
0
,
i
=
1
, 2,
3
样本带入得:
1
2
(
18
α
1
2
+
25
α
2
2
+
2
α
3
2
+
42
α
1
α
2
−
12
α
1
α
3
−
14
α
2
α
3
)
−
α
1
−
α
2
−
α
3
把
α
1
+
α
2
−
α
3
=
0
⇒
α
1
+
α
2
=
α
3
得:
L
(
α
)
=
4
α
1
2
+
13
2
α
2
2
+
10
α
1
α
2
−
2
α
1
−
2
α
2
分别对参数求导得:
∂
L
∂
α
1
=
8
α
1
+
10
α
2
−
2
=
0
∂
L
∂
α
2
=
13
α
2
+
10
α
1
−
2
α
2
=
0
解得:
α
1
=
1.5
,
α
2
=
−
1
不满足条件:
α
i
≥
0
,
i
=
1
,
2,
3
故最终的解应该为边界上的点:
α
1
=
0
,
对
α
2
求偏导,解得
α
2
=
−
2
13
,
不满足条件:
α
i
≥
0
,
i
=
1
,
2,
3
α
2
=
0
,
对
α
1
求偏导,解得
α
1
=
0.25
,
α
1
+
α
2
=
α
3
⇒
α
3
=
0.25
满足所有条件
最小值在
(
0.25
,
0
,
0.25
)
处取得
∵
w
=
∑
i
=
1
N
α
i
y
i
Φ
(
x
i
)
,
b
=
y
i
−
∑
i
=
1
N
α
i
y
i
(
Φ
(
x
i
)
⋅
Φ
(
x
j
)
)
带入
α
(
0.25
,
0
,
0.25
)
得:
w
1
=
w
2
=
0.5
,
b
=
−
2
得到最大间隔分割超平面表达式为
0.5
x
1
+
0.5
x
2
−
2
=
0
.
\\ \text{样本:}x_1\left( 3,\,\,3,\,\,1 \right) ,\,\,x_2=\left( 4,3,1 \right) ,\ x_3=\left( 1,\ 1,\ -1 \right) \\ ~\\ \text{求解:}\frac{1}{2}\sum_{i=1}^n{\sum_{j=1}^n{\alpha _i\alpha _jy_iy_j\left( x_i\cdot x_j \right)}}-\sum_{i=1}^n{\alpha _i},\text{且}\alpha _1+\alpha _2-\alpha _3=0\text{,}\alpha _i\ge 0\text{,\ }i=1\text{,\ 2,\ }3\\ ~\\ \text{样本带入得:}\\ ~\\ \frac{1}{2}\left( 18\alpha _{1}^{2}+25\alpha _{2}^{2}+2\alpha _{3}^{2}+42\alpha _1\alpha _2-12\alpha _1\alpha _3-14\alpha _2\alpha _3 \right) -\alpha _1-\alpha _2-\alpha _3\\ ~\\ \text{把}\alpha _1+\alpha _2-\alpha _3=0\Rightarrow \alpha _1+\alpha _2=\alpha _3\text{得:}\\ ~\\ L\left( \alpha \right) =4\alpha _{1}^{2}+\frac{13}{2}\alpha _{2}^{2}+10\alpha _1\alpha _2-2\alpha _1-2\alpha _2\\ ~\\ \text{分别对参数求导得:}\\ ~\\ \frac{\partial L}{\partial \alpha _1}=8\alpha _1+10\alpha _2-2=0\\ ~\\ \frac{\partial L}{\partial \alpha _2}=13\alpha _2+10\alpha _1-2\alpha _2=0\\ ~\\ \text{解得:}\alpha _1=1.5\text{,\ }\alpha _2=-1\ \text{不满足条件:}\alpha _i\ge 0\text{,\,\,}i=1\text{,\,\,2,\,\,}3\\ ~\\ \text{故最终的解应该为边界上的点:}\\ ~\\ \alpha _1=0\text{,\,\,对}\alpha _2\text{求偏导,解得}\alpha _2=-\frac{2}{13},\ \text{不满足条件:}\alpha _i\ge 0\text{,\,\,}i=1\text{,\,\,2,\,\,}3\\ ~\\ \,\alpha _2=0,\ \text{对}\alpha _1\text{求偏导,解得}\alpha _1=0.25\text{,}\alpha _1+\alpha _2=\alpha _3\Rightarrow \alpha _3=0.25\ \text{满足所有条件}\\ ~\\ \text{最小值在}\left( 0.25,\ 0,0.25 \right) \text{处取得\ }\\ ~\\ \because w=\sum_{i=1}^N{\alpha _iy_i\varPhi \left( x_i \right)},b=y_i-\sum_{i=1}^N{\alpha _iy_i\left( \varPhi \left( x_i \right) \cdot \varPhi \left( x_j \right) \right)}\\ ~\\ \text{带入}\alpha \left( 0.25,\,\,0,0.25 \right) \text{得:}\\ ~\\ w_1=w_2=0.5,b=-2\\ ~\\ \text{得到最大间隔分割超平面表达式为}0.5x_1+0.5x_2-2=0\\ ~\\ \\.
样本:x1(3,3,1),x2=(4,3,1), x3=(1, 1, −1) 求解:21∑i=1n∑j=1nαiαjyiyj(xi⋅xj)−∑i=1nαi,且α1+α2−α3=0,αi≥0, i=1, 2, 3 样本带入得: 21(18α12+25α22+2α32+42α1α2−12α1α3−14α2α3)−α1−α2−α3 把α1+α2−α3=0⇒α1+α2=α3得: L(α)=4α12+213α22+10α1α2−2α1−2α2 分别对参数求导得: ∂α1∂L=8α1+10α2−2=0 ∂α2∂L=13α2+10α1−2α2=0 解得:α1=1.5, α2=−1 不满足条件:αi≥0,i=1,2,3 故最终的解应该为边界上的点: α1=0,对α2求偏导,解得α2=−132, 不满足条件:αi≥0,i=1,2,3 α2=0, 对α1求偏导,解得α1=0.25,α1+α2=α3⇒α3=0.25 满足所有条件 最小值在(0.25, 0,0.25)处取得 ∵w=∑i=1NαiyiΦ(xi),b=yi−∑i=1Nαiyi(Φ(xi)⋅Φ(xj)) 带入α(0.25,0,0.25)得: w1=w2=0.5,b=−2 得到最大间隔分割超平面表达式为0.5x1+0.5x2−2=0 .
观察上图我们能够发现:我们在求解分割超平面时由于
α
2
=
0
\alpha _2=0
α2=0,所以我们其实并没有用到。
所以支持向量机的本质就是:在能够完全分开两类样本的前提下,找到相应的支持向量(本例中
x
1
,
x
3
x _1,x_3
x1,x3(离分割线最近的两个向量))来支撑分割超平面使得间隔最小。






















 2349
2349

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








