传统的序列模型HMM实现和优劣势

1. HMM模型介绍

隐马尔可夫模型（Hidden Markov Model，HMM）是一种用于建模时序数据的统计模型，它由一个隐藏的马尔可夫链和一个观测序列组成。隐藏的马尔可夫链对应于不可观测的状态序列，观测序列对应于可观测的结果序列。HMM的基本假设是当前时刻的状态仅与前一时刻的状态有关，并且当前时刻的观测仅与当前时刻的状态有关。

HMM的核心要素包括状态集合（包括初始状态和转移概率）和观测集合（包括观测概率）。HMM模型可以用于很多应用领域，如语音识别、自然语言处理、生物信息学等。

2. HMM优势

• HMM能够处理时序数据：HMM适用于对时序数据进行建模，能够捕捉观测数据之间的时序关系。
• 可解释性强：HMM模型的参数包括状态转移概率和观测概率，这些参数具有一定的物理意义，能够提供对模型结果的解释。
• 训练简单：HMM的参数可以通过最大似然估计或基于EM算法的训练方法来学习，相对较为简单。

3. HMM劣势

• 独立性假设限制：HMM模型假设当前时刻的状态仅与前一时刻的状态有关，这种独立性假设在某些实际情况下可能不成立，导致模型性能下降。
• 难以处理长程依赖：由于HMM的状态转移仅与前一时刻的状态有关，因此难以捕捉长程依赖的关系，对于长序列的建模效果较差。
• 难以处理高维数据：对于高维的观测数据，HMM模型需要估计大量的参数，导致模型复杂度增加。

4. HMM模型实现

下面将通过一个简单的例子来实现HMM模型，以便更好地理解HMM的原理和实现过程。

参数介绍

在HMM模型中，需要定义的参数包括状态集合、初始状态概率、状态转移概率和观测概率。假设我们有3个隐藏状态和2种观测结果，参数可以定义如下：

• 隐藏状态集合：S = {s1, s2, s3}
• 初始状态概率：π = [0.2, 0.4, 0.4]
• 状态转移概率：A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]
• 观测概率：B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]

完整代码案例

import numpy as np class HMM: def __init__(self, N, M): self.N = N # 隐藏状态数 self.M = M # 观测符号数 def forward(self, O, A, B, pi): T = len(O) # 观测序列长度 alpha = np.zeros((T, self.N)) # 前向概率矩阵 # 初始化 for i in range(self.N): alpha[0, i] = pi[i] * B[i, O[0]] # 递推 for t in range(T - 1): for j in range(self.N): alpha[t + 1, j] = np.dot(alpha[t], A[:, j]) * B[j, O[t + 1]] # 终止 P = np.sum(alpha[T - 1]) return P, alpha def backward(self, O, A, B, pi): T = len(O) # 观测序列长度 beta = np.zeros((T, self.N)) # 后向概率矩阵 # 初始化 beta[T - 1] = 1 # 递推 for t in range(T - 2, -1, -1): for i in range(self.N): beta[t, i] = np.sum(A[i] * B[:, O[t + 1]] * beta[t + 1]) # 终止 P = np.sum(pi * B[:, O[0]] * beta[0]) return P, beta def viterbi(self, O, A, B, pi): T = len(O) # 观测序列长度 delta = np.zeros((T, self.N)) # 最大路径概率矩阵 psi = np.zeros((T, self.N), dtype=int) # 最优路径矩阵 # 初始化 for i in range(self.N): delta[0, i] = pi[i] * B[i, O[0]] # 递推 for t in range(1, T): for j in range(self.N): delta[t, j] = np.max(delta[t - 1] * A[:, j]) * B[j, O[t]] psi[t, j] = np.argmax(delta[t - 1] * A[:, j]) # 终止 P = np.max(delta[T - 1]) I = np.argmax(delta[T - 1]) # 最优路径回溯 path = [I] for t in range(T - 2, -1, -1): I = psi[t + 1, I] path.insert(0, I) return P, path # 定义参数 N = 3 # 隐藏状态数 M = 2 # 观测符号数 A = np.array([[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]) # 状态转移概率 B = np.array([[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]) # 观测概率 pi = np.array([0.2, 0.4, 0.4]) # 初始状态概率 O = [0, 1, 0] # 观测序列 model = HMM(N, M) P1, alpha = model.forward(O, A, B, pi) P2, beta = model.backward(O, A, B, pi) P3, path = model.viterbi(O, A, B, pi) print("前向算法计算的观测序列概率：", P1) print("后向算法计算的观测序列概率：", P2) print("最优路径及其概率：", path, P3)

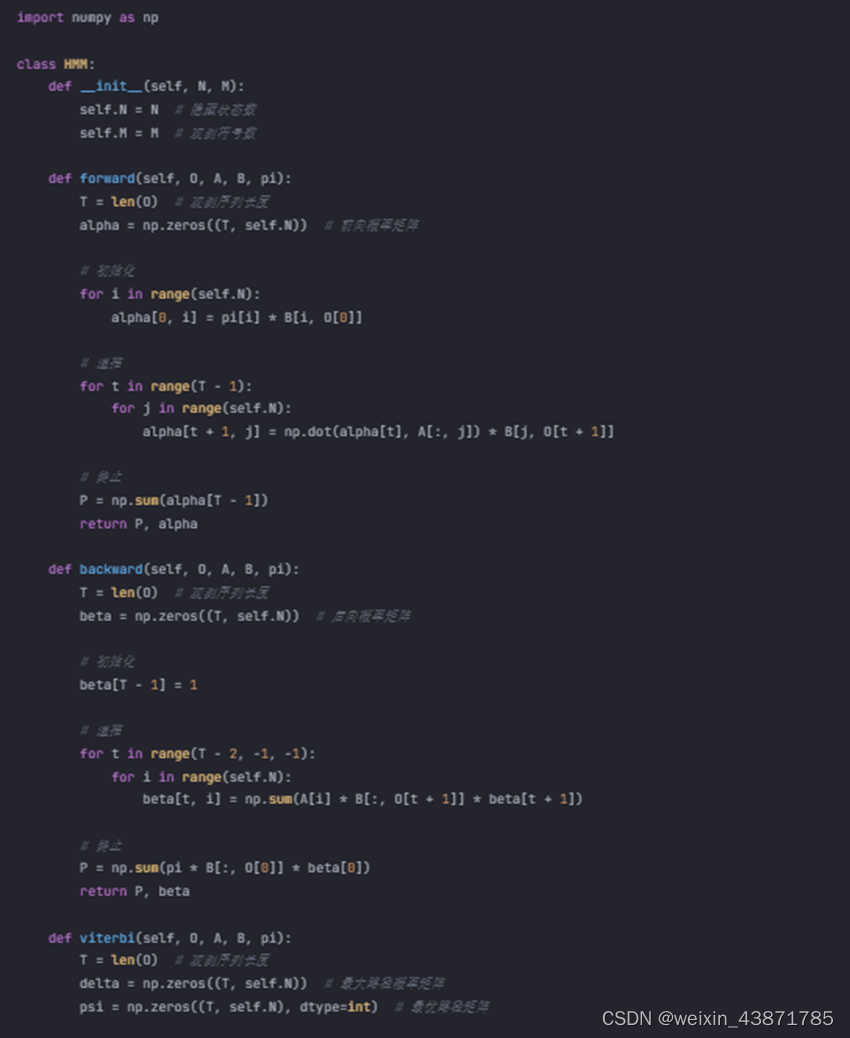
在上面的代码中，我们定义了一个HMM类，其中包括了前向算法、后向算法和维特比算法的实现。我们使用一个简单的例子来对这些方法进行测试，并输出计算结果。

通过上面的代码案例，我们可以看到HMM模型的实现过程，以及如何通过代码来计算观测序列的概率和最优路径。

总结

HMM模型是一种经典的序列模型，它能够有效地捕捉时序数据之间的关系，并且具有一定的可解释性。然而，HMM模型也存在一些局限性，如对独立性假设的限制和对长程依赖关系的难以处理。因此，在实际应用中需要根据具体问题选择合适的模型，并结合其他技术对模型进行改进。