数据的偏度和峰度理解 + log消除 + python

最新推荐文章于 2024-01-12 11:41:21 发布
最新推荐文章于 2024-01-12 11:41:21 发布
阅读量6.2k 收藏 6
点赞数 2
分类专栏： 数据处理 文章标签： 偏度 峰度 理解 消除 python
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_43909872/article/details/86486258
版权
本文介绍了偏度和峰度在数据统计中的意义，偏度反映分布对称性，峰度表示数据分布的尖锐程度。通过Python实验，创建正态分布数据并人为增加偏度和峰度，然后使用自然对数消除异常值，观察统计特性变化。同时指出网上部分计算skewness和kurtosis的Python代码存在的错误，并提供了修正后的正确代码。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

晚上看神经网络的feature工程看到对偏度数据进行处理，已经忘了。。。查阅了一些资料，顺便写个小程序比较一下，记录下来

关于偏度和峰度的定义不再赘述，有很多文章
简单来说对于数据统计：

  1. 偏度能够反应分布的对称情况，右偏（也叫正偏），在图像上表现为数据右边脱了一个长长的尾巴，这时大多数值分布在左侧，有一小部分值分布在右侧。

  2. 峰度反应的是图像的尖锐程度：峰度越大，表现在图像上面是中心点越尖锐。在相同方差的情况下，中间一大部分的值方差都很小，为了达到和正太分布方差相同的目的，必须有一些值离中心点越远，所以这就是所说的“厚尾”，反应的是异常点增多这一现象。

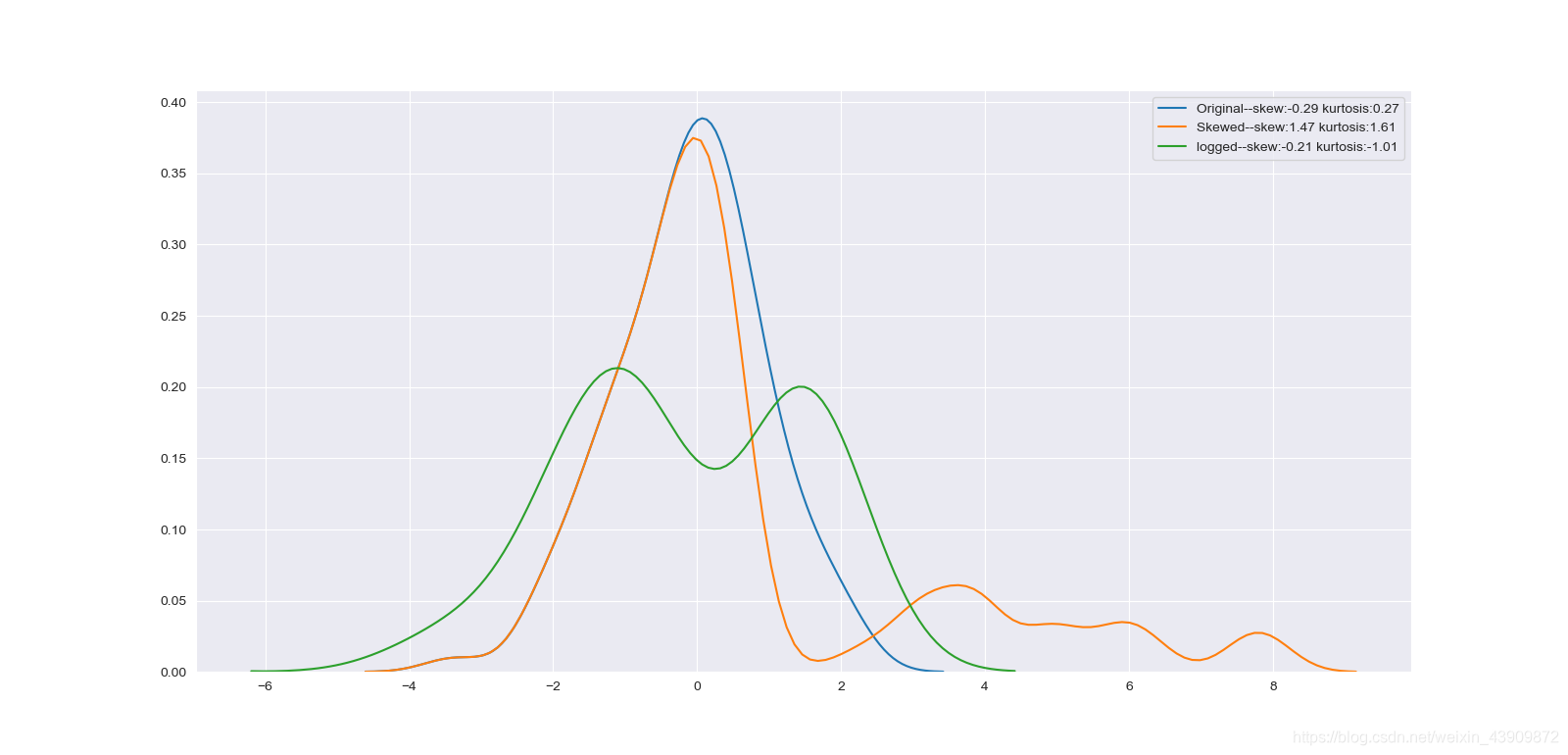
Python的实验：

a. 先构造一个正态分布的随机100个数
b. 把排序后比较大的20个数*4，造成偏度和峰度都变大的数据
c. 把所有数据都取自然对数，再看偏度和峰度

实验结果：
可以看到b操作增加了右边的尾巴厚度，直接增大了skewness和kurtosis的值，造成了正偏分布，而对所有数取log又把数据的概率密度扁平化了，减小了这两个值

PS：网上流传最多的直接用python计算skewness和kurtosis的代码是有错误的，下面贴了改动后的正确代码，这个例子是直接用pandas自带的函数算的
在这里插入图片描述

实验代码：

最低0.47元/天 解锁文章
python数据分析---ch11 python数据描述性统计
爱数据爱统计
06-16 1510
零基础入门，python描述性统计
深度学习中处理偏差和方差
qq_37454669的博客
07-11 926
初始模型训练完成后，首先要知道算法的偏差高不高 如果偏差较高，试着评估训练集或训练数据的性能。如果偏差的确很高，甚至无法拟合训练集，那么你要做的就是： 选择一个新的网络，比如含有更多隐藏层或者隐藏单元的网络， 花费更多时间来训练网络， 或者尝试更先进的优化算法， 你也可以尝试其他方法，可能有用，也可能没用。 采用规模更大的网络通常都会有所帮助，延长训练时间不一定有用，但也没什么坏处。 训练学习算法时，需要不断尝试这些方法，直到解决掉偏差问题，这是最低标准，反复尝试，直到可以拟合数据为止，至少能够拟合训练
特征工程 - 数据分析 - 峰度 and 偏度
GoWeiXH的小天地
05-13 4419
特征工程 - 数据分析 - 峰度 and 偏度偏度峰度 偏度 偏度（Skewness）用来描述数据分布的对称性。 当偏度 <0 时，称为负偏，数据出现左侧长尾； 当偏度>0时，称为正偏，数据出现右侧长尾。 正态分布是对称的，其偏度为 0。 当数据偏度为 0 时，表示数据相对均匀的分布在平均值两侧，但不一定是正态分布。 当偏度绝对值过大时，长尾的一侧出现极端值的可能性较高。 下图...
当一堆数据差异过大如何选？
me211yjs的博客
01-12 1286
对于每个数据点，中值滤波会考虑包含该点及其邻近数据点的窗口，然后计算窗口中所有数据点的中值，并将该中值作为滤波后的值。计算每个数据点及其相邻数据点的平均值，可以使用不同的窗口大小。这有助于平滑数据并减小突然的差异。将每个数据点及其相邻数据点的值进行排序，然后选择中间值作为新的数据点。计算相邻数据点之间的差异，然后根据一定规则进行处理，例如替换为平均值或通过插值进行修正。将与相邻数据相比差异过大的数据点视为异常值，并根据设定的阈值进行剔除或修正。在中值滤波中，窗口大小是指用于计算中值的数据点的数量。
大数据----“数据倾斜”的问题
fct2001140269的博客
10-14 4478
解决数据倾斜的办法，前辈已经写得非常完整了，我这里就直接搬砖吧 （建议先看这个链接文章，非常好） https://blog.csdn.net/chyeers/article/details/78320778 下面是自己的总结： 一、Hadoop中的数据倾斜： 什么是数据倾斜？（见下图） 简单来说数据倾斜就是数据的key 的分化严重不均，造成一部分数据很多，一部分数据很少的局面。 举个 wo...
大数据数据倾斜问题与企业级解决方案
赵广陆
07-21 938
数据倾斜问题 在实际工作中，如果我们想提高MapReduce的执行效率，最直接的方法是什么呢？ 我们知道MapReduce是分为Map阶段和Reduce阶段，其实提高执行效率就是提高这两个阶段的执行效 率默认情况下Map阶段中Map任务的个数是和数据的InputSplit相关的，InputSplit的个数一般是和Block块 是有关联的，所以可以认为Map任务的个数和数据的block块个数有关系，针对Map任务的个数我们一般 是不需要干预的，除非是前面我们说的海量小文件，那个时候可以考虑把小文件合并成大文件
机器学习特征工程经验总结一
TURING.DT
09-05 1793
这块内容分为两篇文章，有一点长，但内容很实用，建议耐心的看一下。 机器学习特征工程经验总结一机器学习特征工程经验总结二 -------------------------------------------- 很多人其实非常好奇BAT里机器学习算法工程师平时工作内容是怎样？其实大部分人都是在跑数据，各种map-reduce，hive SQL，数据仓库搬砖，数据清洗、数据清洗、数据清洗，业务分...
数据分布的秘密：偏度和峰度的应用与案例
![偏度和峰度-数据统计分析及方法SPSS教程完整版]...此外，本文探讨了偏度和峰度在数据分析中的实际应用，如描述性统计、异常值检测、数据标准化等，并通过案例研究分析了它们在市场研究和机器学习中的
【数据可视化艺术】：偏度和峰度，美化图表的关键
通过理论分析和案例研究，本文阐述了偏度和峰度如何影响数据的展示效果，并探讨了它们在各种图表类型中的应用。同时，论文提出了实践技巧，帮助读者选择合适的图表类型，并介绍了高级美化技巧以增强图表的表现力。...
计算日对数收益率的样本均值，方差、偏度和峰度
最新发布
10-01
计算金融时间序列中的日对数收益率（Logarithmic Return）的统计特性，如样本均值、方差、偏度和峰度，可以帮助我们理解资产价格波动的特征。以下是这些概念的简单解释： 1. **样本均值** (Mean): 它是所有日对数...
回归分析-正态分布总结
txmmy的博客
11-30 1927
6.数据标准化只能将一个正态分布变成标准正态分布，并不能将偏态数据变成正态分布，所以，数据标准化处理的是正态分布数据峰度不等于3（标准正态分布）和正态数据的均值不为0的情况。5.数据标准化的意义主要是，在回归问题中，可以使得各变量更具有可比性，同时分析结果更容易满足回归分析的残差假定。1.数据不是标准正态分布的主要原因，来源于数据的偏度和峰度。QuantileTransformer：映射到均匀分布。4.另外数据的标准化，不能将偏态数据变成正态分布。3.处理峰度的通常方式是数据的标准化。
t-ekurtosis:学生的t分布过多峰度
05-17
峰度过高 [学生t]（ 学生t_distribution）分布。 [学生t]（ 学生t_distribution）随机变量的为 v > 0是分布的自由度。 对于任何v <= 2 ，是不确定的。 在这种情况下，此模块将返回NaN。 安装 $ npm install distributions-t-ekurtosis 要在浏览器中使用，请使用 。 用法 var ekurtosis = require ( 'distributions-t-ekurtosis' ) ; 精神病（v [，opts]） 计算具有参数v的[学生t]（ 学生t_distribution）分布的峰度。 v可以是number ， array ，typed array或matrix 。 var matrix = require ( 'dstructs-matrix' ) , data , mat , ou
统计基础—数据集中趋势、离散程度、偏度与峰度的衡量指标(1)
weixin_50304531的博客
03-29 4993
集中趋势 离散程度 偏度和峰度
峰度（Kurtosis）和偏度（Skewness）
weixin_30954265的博客
05-15 9593
峰度（Kurtosis） 定义 峰度又称峰态系数，表征概率密度分布曲线在平均值处峰值高低的特征数，即是描述总体中所有取值分布形态陡缓程度的统计量。直观看来，峰度反映了峰部的尖度。这个统计量需要与正态分布相比较。 公式 定义上峰度是样本的标准四阶中心矩（standardized 4rd central moment)。 随机变量的峰度计算方...
峰度和偏度
读万卷书 行万里路
10-17 1万+
1.峰度 1.1 峰度的定义   峰度(kurtosis)，又称峰态系数，是表征概率密度分布曲线在平均值处峰值高低的指标。直观地说，这个指标反映地是峰部的尖度。该指标的计算是相对于正态分布而言的，如果峰度大于3，则说明峰的形状比较尖，比正态分布要陡峭。在统计学中，**峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。**对于具有nnn个值的样本，其峰度的计算公式如下：g2=m4m22=1n∑i=1n(xi−x‾)4(1n∑i=1n(xi−x‾)2)2−3g_{2}=\frac{m_{4}}
偏度和峰度
倚树探星的博客
10-08 3072
numpy和pandas负责把数据准备好 matplotlib负责把数据制作成图 偏度和峰度 偏度 衡量对称性 偏度>0，说明随机变量x右边偏离均值比较多，这样的数据分布称为右偏或者正偏。 偏度>0，说明随机变量x左边偏离均值比较多，这样的数据分布称为左偏或者负偏。 峰度 峰度衡量偏度 峰度比较大，说明随机变量x偏离均值的极端值比较多 峰度比较小，说明随机变量x偏离均值的极端值比较少 ...
数据预处理——样本分布（正态分布、偏态分布）
热门推荐
csdn_lzw的博客
10-25 6万+
转载自： https://blog.csdn.net/lanchunhui/article/details/53239441 https://www.cnblogs.com/gczr/p/6802998.html 一、何为数据的偏态分布？ 频数分布有正态分布和偏态分布之分。正态分布是指多数频数集中在中央位置，两端的频数分布大致对称。 偏态分布是指频数分布不对称，集中位置偏向一侧。若集中位置偏向数值...
数据倾斜的处理方案有哪些？
SunGirl0007的博客
07-04 3787
数据倾斜
如何处理偏态数据？
data_cola的博客
06-08 1万+
这是笔试/面试题系列的第2篇文章 在了解何为偏态数据前，要先从正态数据说起。 正态分布 正态分布是自然界中广泛存在的，我们都知道它是两头低，中间高，整个形态呈现对称钟形的一个分布，之所以叫正态分布，是因为在大量连续数据测量的情况下，我们比较希望看到这种状态，一个标准的正态分布是u（均值）=0，σ（标准差）=1。 从下图可以看出，横坐标代表随机变量X的一个取值，在均值（u=0）附近概率密度最大，越偏离均值，概率密度减小，不在(u-3σ,u+3σ)范围内的数据就属于统计学意义上的异常值了。 ..
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值