线性判别分析
线性判别分析中有降维,把数据都投影到同一条线上,然后在直线上取一个阈值,将直线分成两条射线,每一条代表一个分类。会损失一些数据信息,但如果这些信息是一些干扰信息,丢失也未尝不是好事。
线性判别分析之后的结果是一个向量,其他的不行吗?
主要指导思想(目标):类内小,类间大。
公式推导
我们得到的是向量,为了方便计算损失,不妨设 ∣ ∣ w ∣ ∣ = 1 ||\pmb w||=1 ∣∣ww∣∣=1,每一个数据 X i \pmb X_i XXi看作一个向量。那么 X i w \pmb X_i\pmb w XXiww是每个数据在 w \pmb w ww方向上的投影。与 w \pmb w ww的其中一个平面是划分平面。
两个不同类别分别命名为
C
1
C_1
C1和
C
2
C_2
C2,用
μ
\pmb\mu
μμ,
μ
C
1
\pmb\mu_{C_1}
μμC1,
μ
C
2
\pmb\mu_{C_2}
μμC2分别代表全部数据,
C
1
C_1
C1数据,
C
2
C_2
C2数据的均值,用
Σ
\pmb\Sigma
ΣΣ,
Σ
C
1
\pmb\Sigma_{C_1}
ΣΣC1,
Σ
C
2
\pmb\Sigma_{C_2}
ΣΣC2分别代表全部数据,
C
1
C_1
C1数据,
C
2
C_2
C2数据的协方差矩阵。
μ
~
\tilde{\mu}
μ~和
σ
~
2
\tilde{\sigma}^2
σ~2表示投影的均值和方差。
μ = 1 N ∑ 1 N X i μ C 1 = 1 N C 1 ∑ 1 N C 1 X C 1 i μ C 2 = 1 N C 2 ∑ 1 N C 2 X C 1 i Σ = 1 N ∑ 1 N ( X i − μ ) ( X i − μ ) T Σ C 1 = 1 N C 1 ∑ 1 N C 1 ( X C 1 i − μ C 1 ) ( X C 1 i − μ C 1 ) T Σ C 2 = 1 N C 2 ∑ 1 N C 2 ( X C 2 i − μ C 2 ) ( X C 2 i − μ C 2 ) T {\LARGE \begin{array}{ccl} \pmb\mu &=& \frac{1}{N} \sum_1^{N}\pmb X_i \\ \pmb\mu_{C_1} &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}\pmb X_{C_1i} \\ \pmb\mu_{C_2} &=& \frac{1}{N_{C_2}} \sum_1^{N_{C_2}}\pmb X_{C_1i}\ \\ \pmb\Sigma &=& \frac{1}{N} \sum_1^{N}(\pmb X_i -\pmb\mu)(\pmb X_i -\pmb\mu)^T \\ \pmb\Sigma_{C_1} &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}(\pmb X_{C_1i} -\pmb\mu_{C_1} )(\pmb X_{C_1i} -\pmb\mu_{C_1} )^T\\ \pmb\Sigma_{C_2} &=& \frac{1}{N_{C_2}} \sum_1^{N_{C_2}}(\pmb X_{C_2i} -\pmb\mu_{C_2} )(\pmb X_{C_2i} -\pmb\mu_{C_2} )^T\\ \end{array} } μμμμC1μμC2ΣΣΣΣC1ΣΣC2======N1∑1NXXiNC11∑1NC1XXC1iNC21∑1NC2XXC1i N1∑1N(XXi−μμ)(XXi−μμ)TNC11∑1NC1(XXC1i−μμC1)(XXC1i−μμC1)TNC21∑1NC2(XXC2i−μμC2)(XXC2i−μμC2)T
μ ~ = 1 N ∑ 1 N X i θ μ ~ C 1 = 1 N C 1 ∑ 1 N C 1 X C 1 i θ μ ~ C 2 = 1 N C 2 ∑ 1 N C 2 X C 2 i θ σ ~ 2 = 1 N ∑ 1 N ( X i θ − μ ~ ) 2 σ ~ C 1 2 = 1 N C 1 ∑ 1 N C 1 ( X C 1 i θ − μ ~ C 1 ) 2 σ ~ C 2 2 = 1 N C 2 ∑ 1 N C 2 ( X C 2 i θ − μ ~ C 2 ) 2 {\LARGE \begin{array}{ccl} \tilde\mu &=& \frac{1}{N} \sum_1^{N}\pmb X_i\pmb \theta \\ \tilde\mu_{C_1} &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}\pmb X_{C_1i}\pmb \theta \\ \tilde\mu_{C_2} &=& \frac{1}{N_{C_2}} \sum_1^{N_{C_2}}\pmb X_{C_2i}\pmb \theta \\ \tilde\sigma^2 &=& \frac{1}{N} \sum_1^{N}(\pmb X_i\pmb \theta -\tilde\mu)^2 \\ \tilde\sigma_{C_1}^2 &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}(\pmb X_{C_1i}\pmb \theta -\tilde\mu_{C_1} )^2\\ \tilde\sigma_{C_2}^2 &=& \frac{1}{N_{C_2}} \sum_1^{N_{C_2}}(\pmb X_{C_2i}\pmb \theta -\tilde\mu_{C_2} )^2\\ \end{array} } μ~μ~C1μ~C2σ~2σ~C12σ~C22======N1∑1NXXiθθNC11∑1NC1XXC1iθθNC21∑1NC2XXC2iθθN1∑1N(XXiθθ−μ~)2NC11∑1NC1(XXC1iθθ−μ~C1)2NC21∑1NC2(XXC2iθθ−μ~C2)2
类间: ( μ ~ C 1 − μ ~ C 2 ) 2 (\tilde\mu_{C_1}-\tilde\mu_{C_2})^2 (μ~C1−μ~C2)2
类内: σ ~ C 1 2 + σ ~ C 2 2 \tilde\sigma^2_{C_1}+\tilde\sigma^2_{C_2} σ~C12+σ~C22
目标函数: J ( θ ) = ( μ ~ C 1 − μ ~ C 2 ) 2 σ ~ C 1 2 + σ ~ C 2 2 J(\pmb \theta) = \frac{(\tilde\mu_{C_1}-\tilde\mu_{C_2})^2}{\tilde\sigma^2_{C_1}+\tilde\sigma^2_{C_2}} J(θθ)=σ~C12+σ~C22(μ~C1−μ~C2)2
J
(
θ
)
=
(
μ
~
C
1
−
μ
~
C
2
)
2
σ
~
C
1
2
+
σ
~
C
2
2
分子
=
(
μ
~
C
1
−
μ
~
C
2
)
2
=
(
1
N
C
1
∑
1
N
C
1
X
C
1
i
θ
−
1
N
C
2
∑
1
N
C
2
X
C
2
i
θ
)
2
=
(
(
μ
C
1
−
μ
C
2
)
θ
)
2
=
θ
T
(
μ
C
1
−
μ
C
2
)
T
(
μ
C
1
−
μ
C
2
)
θ
σ
~
C
1
2
=
1
N
C
1
∑
1
N
C
1
(
X
C
1
i
θ
−
μ
~
C
1
)
2
=
1
N
C
1
∑
1
N
C
1
(
X
C
1
i
θ
−
1
N
C
1
∑
1
N
C
1
X
C
1
i
θ
)
2
=
1
N
C
1
∑
1
N
C
1
(
(
X
C
1
i
−
1
N
C
1
∑
1
N
C
1
X
C
1
i
)
θ
)
2
=
1
N
C
1
∑
1
N
C
1
(
(
X
C
1
i
−
μ
C
1
)
θ
)
2
=
1
N
C
1
∑
1
N
C
1
θ
T
(
X
C
1
i
−
μ
C
1
)
T
(
X
C
1
i
−
μ
C
1
)
θ
=
θ
T
(
1
N
C
1
∑
1
N
C
1
(
X
C
1
i
−
μ
C
1
)
T
(
X
C
1
i
−
μ
C
1
)
)
θ
=
θ
T
Σ
C
1
θ
σ
~
C
2
2
=
θ
T
Σ
C
2
θ
分母
=
θ
T
Σ
C
1
θ
+
θ
T
Σ
C
2
θ
=
θ
T
(
Σ
C
1
+
Σ
C
2
)
θ
{\LARGE \begin{array}{ccl} J(\pmb \theta) &=& \frac{(\tilde\mu_{C_1}-\tilde\mu_{C_2})^2}{\tilde\sigma^2_{C_1}+\tilde\sigma^2_{C_2}}\\ 分子&=&(\tilde\mu_{C_1}-\tilde\mu_{C_2})^2\\ &=&(\frac{1}{N_{C_1}} \sum_1^{N_{C_1}}\pmb X_{C_1i}\pmb \theta- \frac{1}{N_{C_2}} \sum_1^{N_{C_2}}\pmb X_{C_2i}\pmb \theta)^2\\ &=&((\pmb\mu_{C_1}-\pmb\mu_{C_2})\pmb \theta)^2\\ &=&\pmb \theta^T(\pmb\mu_{C_1}-\pmb\mu_{C_2})^T(\pmb\mu_{C_1}-\pmb\mu_{C_2})\pmb \theta\\ \tilde\sigma^2_{C_1} &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}(\pmb X_{C_1i}\pmb \theta -\tilde\mu_{C_1} )^2\\ &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}(\pmb X_{C_1i}\pmb \theta -\frac{1}{N_{C_1}} \sum_1^{N_{C_1}}\pmb X_{C_1i}\pmb \theta )^2\\ &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}((\pmb X_{C_1i} -\frac{1}{N_{C_1}} \sum_1^{N_{C_1}}\pmb X_{C_1i})\pmb \theta )^2\\ &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}((\pmb X_{C_1i} -\pmb\mu_{C_1})\pmb \theta )^2\\ &=& \frac{1}{N_{C_1}} \sum_1^{N_{C_1}}\pmb \theta^T(\pmb X_{C_1i} -\pmb\mu_{C_1})^T(\pmb X_{C_1i} -\pmb\mu_{C_1})\pmb \theta \\ &=& \pmb\theta^T(\frac{1}{N_{C_1}} \sum_1^{N_{C_1}} (\pmb X_{C_1i} -\pmb\mu_{C_1})^T(\pmb X_{C_1i} -\pmb\mu_{C_1}))\pmb \theta \\ &=& \pmb\theta^T\pmb\Sigma_{C_1}\pmb \theta \\ \tilde\sigma^2_{C_2} &=& \pmb\theta^T\pmb\Sigma_{C_2}\pmb \theta\\ 分母&=&\pmb\theta^T\pmb\Sigma_{C_1}\pmb \theta+\pmb\theta^T\pmb\Sigma_{C_2}\pmb \theta\\ &=&\pmb\theta^T(\pmb\Sigma_{C_1}+\pmb\Sigma_{C_2})\pmb \theta\\ \end{array} }
J(θθ)分子σ~C12σ~C22分母===============σ~C12+σ~C22(μ~C1−μ~C2)2(μ~C1−μ~C2)2(NC11∑1NC1XXC1iθθ−NC21∑1NC2XXC2iθθ)2((μμC1−μμC2)θθ)2θθT(μμC1−μμC2)T(μμC1−μμC2)θθNC11∑1NC1(XXC1iθθ−μ~C1)2NC11∑1NC1(XXC1iθθ−NC11∑1NC1XXC1iθθ)2NC11∑1NC1((XXC1i−NC11∑1NC1XXC1i)θθ)2NC11∑1NC1((XXC1i−μμC1)θθ)2NC11∑1NC1θθT(XXC1i−μμC1)T(XXC1i−μμC1)θθθθT(NC11∑1NC1(XXC1i−μμC1)T(XXC1i−μμC1))θθθθTΣΣC1θθθθTΣΣC2θθθθTΣΣC1θθ+θθTΣΣC2θθθθT(ΣΣC1+ΣΣC2)θθ
∴
{\LARGE \therefore}
∴
J ( θ ) = θ T ( μ C 1 − μ C 2 ) T ( μ C 1 − μ C 2 ) θ θ T ( Σ C 1 + Σ C 2 ) θ {\LARGE \begin{array}{ccl} J(\pmb \theta) &=& \frac{\pmb \theta^T(\pmb\mu_{C_1}-\pmb\mu_{C_2})^T(\pmb\mu_{C_1}-\pmb\mu_{C_2})\pmb \theta}{\pmb\theta^T(\pmb\Sigma_{C_1}+\pmb\Sigma_{C_2})\pmb \theta}\\ \end{array} } J(θθ)=θθT(ΣΣC1+ΣΣC2)θθθθT(μμC1−μμC2)T(μμC1−μμC2)θθ
设 S b = ( μ C 1 − μ C 2 ) T ( μ C 1 − μ C 2 ) S_b = (\pmb\mu_{C_1}-\pmb\mu_{C_2})^T(\pmb\mu_{C_1}-\pmb\mu_{C_2}) Sb=(μμC1−μμC2)T(μμC1−μμC2), S w = Σ C 1 + Σ C 2 S_w = \pmb\Sigma_{C_1}+\pmb\Sigma_{C_2} Sw=ΣΣC1+ΣΣC2
S b S_b Sb就是类内方差
S w S_w Sw就是类间方差
此时 J ( θ ) = θ T S b θ θ T S w θ {\LARGE J(\pmb \theta) = \frac{\pmb \theta^T S_b \pmb \theta}{\pmb\theta^TS_w\pmb \theta}} J(θθ)=θθTSwθθθθTSbθθ
求导
∂ J ( θ ) ∂ θ = ∂ θ T S b θ θ T S w θ ∂ θ = ∂ ( θ T S b θ ( θ T S w θ ) − 1 ) ∂ θ = ∂ ( θ T S b θ ) ∂ θ ( θ T S w θ ) − 1 + θ T S b θ ∂ ( ( θ T S w θ ) − 1 ) ∂ θ = 2 θ T S b ( θ T S w θ ) − 1 + θ T S b θ ( − 1 ( θ T S w θ ) 2 ) ( 2 θ T S w ) {\LARGE \begin{array}{rcl} \frac{\partial J(\pmb \theta)}{\partial \pmb\theta } &=& \frac{\partial\frac{\pmb \theta^T \pmb S_b \pmb \theta}{\pmb\theta^T\pmb S_w\pmb \theta}}{\partial\pmb\theta}\\ &=& \frac{\partial(\pmb \theta^T \pmb S_b \pmb \theta(\pmb\theta^T\pmb S_w\pmb \theta)^{-1})}{\partial\pmb\theta}\\ &=& \frac{\partial(\pmb \theta^T \pmb S_b \pmb \theta )}{\partial\pmb\theta}(\pmb\theta^T\pmb S_w\pmb \theta)^{-1}+\pmb \theta^T \pmb S_b \pmb \theta \frac{\partial((\pmb\theta^T\pmb S_w\pmb \theta)^{-1})}{\partial\pmb\theta}\\ &=&2\pmb\theta^T\pmb S_b(\pmb\theta^T\pmb S_w\pmb \theta)^{-1}+ \pmb \theta^T \pmb S_b \pmb \theta (- \frac{1}{(\pmb \theta^T \pmb S_w \pmb \theta )^2}) (2\pmb\theta^T\pmb S_w) \end{array} } ∂θθ∂J(θθ)====∂θθ∂θθTSSwθθθθTSSbθθ∂θθ∂(θθTSSbθθ(θθTSSwθθ)−1)∂θθ∂(θθTSSbθθ)(θθTSSwθθ)−1+θθTSSbθθ∂θθ∂((θθTSSwθθ)−1)2θθTSSb(θθTSSwθθ)−1+θθTSSbθθ(−(θθTSSwθθ)21)(2θθTSSw)
令导数等于零
0
=
2
S
b
θ
(
θ
T
S
w
θ
)
−
1
+
θ
T
S
b
θ
(
−
1
(
θ
T
S
w
θ
)
2
)
(
2
S
w
θ
)
2
S
b
θ
(
θ
T
S
w
θ
)
−
1
=
θ
T
S
b
θ
(
1
(
θ
T
S
w
θ
)
2
)
(
2
S
w
θ
)
S
b
θ
(
θ
T
S
w
θ
)
=
(
θ
T
S
b
θ
)
S
w
θ
(
θ
T
S
b
θ
)
S
w
θ
=
S
b
θ
(
θ
T
S
w
θ
)
θ
=
S
w
−
1
θ
T
S
w
θ
θ
T
S
b
θ
S
b
θ
θ
=
S
w
−
1
θ
T
S
w
θ
θ
T
S
b
θ
(
μ
C
1
−
μ
C
2
)
T
(
μ
C
1
−
μ
C
2
)
θ
{\LARGE \begin{array}{rcl} \pmb 0 &=& 2\pmb S_b\pmb\theta(\pmb\theta^T\pmb S_w\pmb \theta)^{-1}+ \pmb \theta^T \pmb S_b \pmb \theta (- \frac{1}{(\pmb \theta^T \pmb S_w \pmb \theta )^2}) (2\pmb S_w\pmb\theta) \\ 2\pmb S_b\pmb\theta(\pmb\theta^T\pmb S_w\pmb \theta)^{-1}&=& \pmb \theta^T \pmb S_b \pmb \theta ( \frac{1}{(\pmb \theta^T \pmb S_w \pmb \theta )^2}) (2\pmb S_w\pmb\theta)\\ \pmb S_b\pmb\theta(\pmb\theta^T\pmb S_w\pmb \theta) &=& (\pmb \theta^T \pmb S_b \pmb \theta )\pmb S_w\pmb\theta\\ (\pmb \theta^T \pmb S_b \pmb \theta )\pmb S_w\pmb\theta &=& \pmb S_b\pmb\theta(\pmb\theta^T\pmb S_w\pmb \theta) \\ \pmb\theta&=& \pmb S_w^{-1}\frac{\pmb \theta^T \pmb S_w \pmb \theta } {\pmb\theta^T\pmb S_b\pmb \theta}\pmb S_b\pmb\theta\\ \pmb\theta &=& \pmb S_w^{-1}\frac{\pmb \theta^T \pmb S_w \pmb \theta } {\pmb\theta^T\pmb S_b\pmb \theta}(\pmb\mu_{C_1}-\pmb\mu_{C_2})^T(\pmb\mu_{C_1}-\pmb\mu_{C_2})\pmb\theta\\ \end{array} }
002SSbθθ(θθTSSwθθ)−1SSbθθ(θθTSSwθθ)(θθTSSbθθ)SSwθθθθθθ======2SSbθθ(θθTSSwθθ)−1+θθTSSbθθ(−(θθTSSwθθ)21)(2SSwθθ)θθTSSbθθ((θθTSSwθθ)21)(2SSwθθ)(θθTSSbθθ)SSwθθSSbθθ(θθTSSwθθ)SSw−1θθTSSbθθθθTSSwθθSSbθθSSw−1θθTSSbθθθθTSSwθθ(μμC1−μμC2)T(μμC1−μμC2)θθ
∵
\because
∵
θ
T
S
w
θ
θ
T
S
b
θ
\frac{\pmb \theta^T \pmb S_w \pmb \theta }{\pmb\theta^T\pmb S_b\pmb \theta}
θθTSSbθθθθTSSwθθ,
(
μ
C
1
−
μ
C
2
)
θ
(\pmb\mu_{C_1}-\pmb\mu_{C_2})\pmb\theta
(μμC1−μμC2)θθ是一个数,不影响
θ
\pmb \theta
θθ的方向
∴
{\LARGE \therefore}
∴
θ
∝
S
w
−
1
(
μ
C
1
−
μ
C
2
)
T
{\LARGE \pmb\theta \propto \pmb S_w^{-1}(\pmb\mu_{C_1}-\pmb\mu_{C_2})^T }
θθ∝SSw−1(μμC1−μμC2)T
i f S w ∝ I {\LARGE \mathcal{{\color{Blue} {if}} } } \pmb S_w \propto \pmb I ifSSw∝II
θ ∝ ( μ C 1 − μ C 2 ) T {\LARGE \pmb \theta \propto (\pmb\mu_{C_1}-\pmb\mu_{C_2})^T } θθ∝(μμC1−μμC2)T
求任意一个点的投影
p r o j θ ( x ) = x T θ {\Large proj_{\pmb \theta}(x) = x^T\pmb\theta } projθθ(x)=xTθθ
求阈值
t h r e s h o l d = N C 1 μ ~ C 1 + N C 2 μ ~ C 1 N C 1 + N C 2 = N C 1 μ C 1 θ + N C 2 μ C 1 θ N C 1 + N C 2 {\Large \begin{array}{rcl} threshold &=& \frac{N_{C_1}\tilde\mu_{C_1}+N_{C_2}\tilde\mu_{C_1}}{N_{C_1}+N_{C_2}}\\ &=& \frac{N_{C_1}\pmb\mu_{C_1}\pmb\theta+N_{C_2}\pmb\mu_{C_1}\pmb\theta}{N_{C_1}+N_{C_2}} \end{array} } threshold==NC1+NC2NC1μ~C1+NC2μ~C1NC1+NC2NC1μμC1θθ+NC2μμC1θθ
依赖
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
人工数据集
n = 100
X = np.random.multivariate_normal((1, 1), [[0.64, 0], [0, 0.64]], size = int(n/2))
X = np.insert(X, 50, np.random.multivariate_normal((3, 3), [[0.64, 0], [0,0.64]], size = int(n/2)),0)
#X = np.insert(X, 0, 1, 1)
m = X.shape[1]
y = np.array([1]*50+[-1]*50).reshape(-1,1)
plt.scatter(X[:50, -2], X[:50, -1])
plt.scatter(X[50:, -2], X[50:, -1], c = "#ff4400")
<matplotlib.collections.PathCollection at 0x7f2b50e680d0>
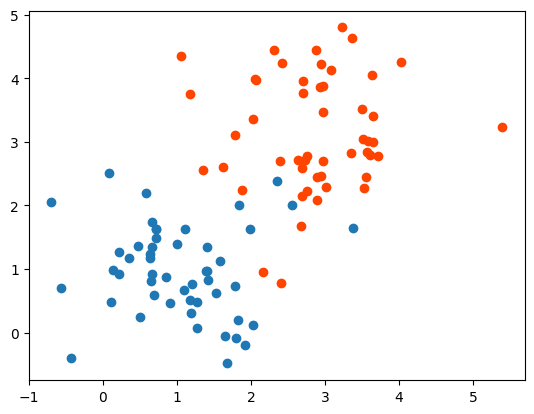
X1 = X[(y==1).reshape(-1)]
X0 = X[(y==-1).reshape(-1)]
n1 = np.array([[X1.shape[0]]])
n0 = np.array([[X0.shape[0]]])
mu1 = X1.mean(axis = 0).reshape(-1,1)
mu0 = X0.mean(axis = 0).reshape(-1,1)
Sigma1 = np.cov(X1.T)
Sigma0 = np.cov(X0.T)
theta = (Sigma1 + Sigma0) @ (mu1 - mu0)
threshold = (n1*mu1 + n0*mu0).T@theta/(n1 + n0)
def getForecast(x):
return x.T @ theta
threshold
array([[-10.45793931]])
预测
print(f'{ 1 if getForecast(np.array([[1],[1]])) > threshold else 0}')
1
分界展示
plt.scatter(X[:50, -2], X[:50, -1])
plt.scatter(X[50:, -2], X[50:, -1], c = "#ff4400")
for i in np.arange(-1,5,0.02):
for j in np.arange(-1,5,0.02):
if abs(getForecast(np.array([[i],[j]])) - threshold) <0.01:
plt.scatter(i,j,c="#000000")
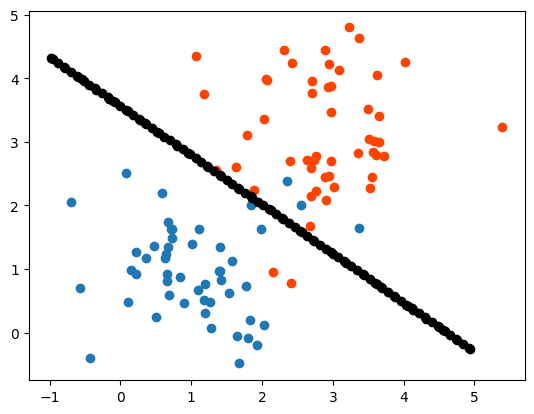






















 1269
1269











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








