Optimization for Data Science学习笔记-3

课程3

主要学习convexity相关知识点。

首先是凸优化理论 convex optimization theory

有几个概念：

1. 凸组合 convex combination
   和凸集没关系，就记“线性组合，系数和为一”。
   

2. 凸包 convex hull
   一些元素的“所有”凸组合的集合就是凸包
   
   

3. proper凸组合
   之前的凸组合只是系数和为1，系数≥0。现在要求系数不为0不为1
   

4. 极点extreme point
   极点是凸集的元素，但是其他的点可以由凸集中的任意两个点的严格（proper?）凸组合表示出来，而极点不行，只有要求一个系数为1和一个系数为0（因为一共就两个系数）时才行。
   

5. 凸集 convex set
   也是任取两点来分析。
   
   
   

6. epigraph
   对于函数而言的概念。
   

7. convex function凸函数
   有了凸集和epigraph–>接下来可以讨论凸函数。
   
   
   ！！！epigraph可以是凸集（如绿色），也可以不是凸集（如红色）！！！利用epigraph是不是凸集可以用来判断函数本身是不是凸函数！！！
   
   要epigraph为凸集，则连线上的点一定要高于or等于函数曲线，所以凸函数的定义为

连线上的点是公式后者，函数上的点是公式前者。
且还有严格凸函数的概念，即连线上的点只能高于函数线。

8. 保凸运算 operations preserving convexity
   a. 非负加权求和 non-negative weighted sum
   凸函数的非负加权求和得到的函数仍为凸函数
   

b. 逐点最大 pointwise maximum

c. 复合 composition
课程里学的是标量复合，其实还有一种矢量符合，区别在于g的domain的维度是1维还是多维的。

d. 复合仿射映射 linear transformation

9. 闭集和开集 closed set / open set
   如果一个集合等于这个集合的闭包 closure，那么它就是闭集。（有边界）
   如果集合的补集是闭集，那么集合是开集。

10. 方向导数 directional derivative
    沿着某个方向d的导数
    

11. 凸性的一阶条件 first order convexity condition
    对于凸函数上的任一点 y ，它所在处的切平面永远在函数 f下方。
    
    
    注意这里是方向导数，方向d是z-y
    凸性的一阶条件可以由凸函数的定义推导得到。（见参考4）

12. 凸性的二阶条件 second order convexity condition
    
    
    可以用凸性的一阶二阶条件证明f是否是凸函数

13. hessian矩阵的定义为
    
    hessian matrix是对称的。
    Q是半正定是指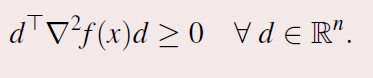
    其中
    
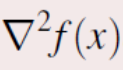
    是Q，d可以想成x
    正定就是
    

则对f是否是凸函数可以用

然后就是凸规划问题 convex programming problem

若最优化问题的目标函数为凸函数，不等式约束函数也为凸函数，（等式约束函数是仿射的，）则称该最优化问题为凸规划。

很多时候我们求解很容易求得local minimum（or maximum），但是不容易求得global。但是对于凸规划问题来说，局部解就是全局解！凸规划可真牛逼！而且如果函数f是严格凸，那么只有一个全局解，也就是只有一个局部解~

所以convexity不管对于set还是funct都很有用！！！

最后是强凸性 strong convexity

强凸性多用在优化中(Optimization)，特别是保证很多基于梯度下降方法的算法的线性收敛速率的条件之一。
函数f是强凸的就是比凸多了一截

如果λ∈(0,1)，那么可以由strong -> strictly；但是不能strictly -x->strong
如果λ∈[0,1]，根本没有这个结论

根据函数是一阶连续可微的，和函数是二阶连续可微的，我们有一些等价的条件用于证明函数的强凸性。

qizhong(ii)可以理解为f is convex enough that even substract a convex fun, f is still convex。
此外，还有一些等价的条件可以在f是强凸性的时得到！！！！！！！！！！（不是证明强凸性）最有名的是PL inequality

这个强凸的性质是很重要的。直观从一维函数来说，一般凸函数只要求函数曲线在其切线之上，至于“上”多少没有要求，也就意味着曲线可以无限“贴着”切线，只要保持在其上就行了。毫无疑问，在优化特别是梯度优化中，这种微弱的梯度变化很难实现快速优化，有可能在有限次数还达不到收敛。如果我们取一个接近最小值的解，这也很难。“非常”接近只是一个定性理解，在这种情况下会出现最优解很近似但是决策变量相差巨大的糟糕情况。这时候，多加一个二次项的，保证有一个二次下界，那么不会出现“贴着”切线的情况，优化也变得更加简单。
有的情况下，没有强凸的条件，可以人为加上一个二次项，以获得强凸特性。

PL不等式的证明
https://zhuanlan.zhihu.com/p/369961719

http://xingyuzhou.org/blog/notes/strong-convexity

参考：https://blog.csdn.net/weixin_44143990/article/details/88703341
https://juejin.cn/post/6889272848993484813
https://blog.csdn.net/hyl1181/article/details/111303984
https://zhuanlan.zhihu.com/p/72660217
https://zhuanlan.zhihu.com/p/369961719
https://blog.csdn.net/qq_41769289/article/details/87694955