电解质溶液的电传导率

1 概述

        在通电、交变磁场等外界作用下，溶液的离子浓度分布变化导致溶液电传导率改变。在电镀、电泳等电化学作业中，需要考虑离子浓度和电传导率之间的相互影响导致的质量问题。

 仿真的电镀层厚度分布（图源：comsol.com）

 

        电解质的水溶液中，溶质发生解离（dissociation），成为若干离子。例如氯化钠（食盐主要成分）会解离成钠离子和氯离子。

氯化钠的解离过程

         根据溶质解离程度，可分为强电解质和弱电解质。强电解质指可以完全解离的溶质，只以带电离子形式存在；弱电解质指不能完全解离的溶质，部分溶质以分子形式存在。常见的强电解质包括硫酸、氢氧化钠等，弱电解质包括碳酸、氢氧化镁等。

        由于离子的存在，溶液会呈现导体的特征。定性而言，等体积溶液离子数量越多则电传导率越大。

        在宏观尺度上，任意区域的溶液均满足电中性条件，即溶液的正离子电荷数和负离子电荷数相等，对外呈现不带电状态。

2 电传导率的定量计算

        为了方便考虑浓度和电传导率之间关系，定义摩尔电传导率（molar conductivity）为溶液电传导率和溶质摩尔浓度的比例值，其国际单位制下的单位为 S*m^2 / mol 。

摩尔电传导率定义

        等量溶质在被稀释时，溶液摩尔电传导率会逐渐加大，原因在于稀释后离子间作用力减小，更容易被外部电场驱动。由于溶质包含的离子总数有限，当被无限多溶质稀释时，溶液的摩尔电传导率存在极限值，称为极限摩尔电传导率（limiting molar conductivity），其仅和溶质化学成分相关。

        在低浓度的前提下，强电解质的摩尔电传导率满足 Debye-Huckel-Onsager 理论：

        其中，A、B 表达式如下图所示：

        A、B的取值仅和溶剂材料属性相关。其中， μ 为溶剂粘度，ε 为溶剂相对介电常数，T 为温度。25°C的纯水，A 为 60.20, B 为 0.229。

        在部分资料中也简写如下，其中 K 称为 Kohlrausch系数。

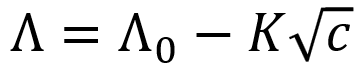
        弱电解质的摩尔电传导率不满足Debye-Huckel-Onsager理论。不断稀释下，由于溶质解离程度增加，其摩尔电传导率会显著增加，不随浓度平方根呈线性变化。

        在低浓度的前提下，弱电解质的摩尔电传导率和溶质解离度 α 为比例关系：

         根据稀释定律，解离常数 K 和解离度 α 关系式如下，其中 c 为溶质浓度

        解离常数是溶液固有属性，因此可得摩尔电传导率和浓度之间的关系。

        不同类型电解质对比如下图所示。

不同类型电解质的摩尔电传导率变化曲线（图源：www.sarthaks.com）

         Kohlrausch法则表明，若离子是可自由迁移的，则溶质各离子的极限摩尔电传导率加权汇总即为溶液的极限摩尔电传导率。

 Kohlrausch法则

        例如硫酸钾（K2SO4）解离为两个钾离子和一个硫酸根离子，其极限摩尔电传导率计算为：

3 外界电磁场的影响

          在通电、交变磁场等外界作用下，溶液中的离子在电场力作用下运动，导致浓度分布发生改变。Nernst-Planck方程描述了在外加的电磁场作用下离子的运动规律，方程形式如下，其中 c 为离子的浓度。

        离子通量 J 的表达式如下所示，等式右边分别为扩散、对流和电迁移项。

        

        若仅通电，无交变磁场，则溶液中电场和电流的分布仅和电势分布相关。