机动目标跟踪——Singer模型
原创不易,路过的各位大佬请点个赞
WX: ZB823618313
机动目标跟踪——Singer模型
1. 对机动目标跟踪的理解
1.1. 对机动目标跟踪的理解
机动目标跟踪一直是目标跟踪领域研究的难点和重点问题。建立目标运动模型和滤波算法是目标跟踪的两个重要因素。由于目标的机动具有不可预测性,使得我们很难建立精确的目标运动模型。如何建立一种有效的模型来反映目标真实的运动轨迹是高机动目标跟踪系统急需解决的问题。经过近三十年的研究,该领域取得了许多重要成果。
个人理解:机动目标跟踪拥有三要素:
被跟踪目标建模(也是本博客重点)
传感器测量(另一个博客介绍)
滤波器设计(见目标跟踪专栏)
从算法层面,在目标跟踪系统中,常用的滤波算法是以卡尔曼滤波器为基本框架的估计算法。卡尔曼滤波器是一种线性、无偏、以误差均方差最小为准则的最优估计算法,它有精确的数学形式和优良的使用效能。卡尔曼滤波方法实质上是一种数据处理方法,它采用递推滤波方法,根据获取的量测数据由递推方程递推给出新的状态估计。由于计算量和存储量小,比较容易满足实时计算的要求,在工程实践中得到广泛应用。
除此之外,非线性滤波也广泛应用与机动目标跟踪,比如:
扩展卡尔曼滤波EKF
无迹卡尔曼滤波UKF
容积卡尔曼滤波CKF
求积卡尔曼滤波QKF
中心差分卡尔曼滤波CDKF
Divided difference filter DDF
高斯混合滤波GSF
强跟踪滤波STF
粒子滤波PF
… …
1.2. 目标模型概述
机动目标模型描述了目标状态随着时间变化的过程。一个好的模型抵得上大量的数据。当前几乎所有的目标跟踪算法都是基于模型进行状态估计的。在卡尔曼滤波器被引入目标跟踪领域后,基于状态空间的机动目标建模成为主要研究对象之一。
常用的目标运动模型包括:
匀速运动模型,CV
匀加速运动模型,CA
匀速转弯模型,CT
Singer 模型
“当前”统计模型
Jerk 模型
目标的空间运动基于不同的运动轨迹和坐标系
一维运动
二维运动
三维运动根据不同方向的运动是否相关
坐标间不耦合模型
坐标间耦合模型
坐标间不耦合模型: 这类模型假设三维空间三个正交方向上的目标机动过程不耦合。目标机动是飞行器受到外力作用而使得加速度变化所致,所以对机动建模的难点在于对目标加速度的描述。对于无机动目标,常速(Constant Velocity,CV〉模型常用于描述这类目标的运动,而常加速度(Constant Acceleration,CA)模型则常用于描述加速度趋近常数的机动目标的运动。
坐标间耦合模型: 坐标间耦合模型绝大多数情况下指的是转弯运动模型。由于此类模型与坐标密切相关,所以可以分为两类:二维转弯模型和三维转弯模型。二维转弯模型又称为平面转弯模型,即CT模型。
2. 一维Singer模型
Singer模型认为机动模型是相关噪声模型,而不是通常假定的白噪声模型,它假定目标加速度
a
(
t
)
a(t)
a(t)不是白噪声模型,而是具有指数自相关的零均值随机过程,其时间相关函数为指数衰减形式:
R
α
(
τ
)
=
E
[
a
(
t
)
a
(
t
+
τ
)
]
=
σ
m
2
e
−
α
∣
τ
∣
,
α
≥
0
R_\alpha(\tau)=E[a(t)a(t+\tau)]=\sigma_m^2e^{-\alpha|\tau|}, \alpha\geq0
Rα(τ)=E[a(t)a(t+τ)]=σm2e−α∣τ∣,α≥0
其中: σ \sigma σ、 a ( t ) a(t) a(t)是在区间 [ t , t + τ ] [t, t+\tau] [t,t+τ]内决定目标机动特性的待定参数。 σ 2 \sigma^2 σ2是目标加速度的方差; α \alpha α为机动时间常数的倒数,即机动频率。
通常α的经验取值范围为:
转弯机动 α = 1 / 60 \alpha=1/60 α=1/60,
逃避机动 α = 1 / 20 \alpha=1/20 α=1/20,
大气扰动 α = 1 \alpha=1 α=1,
它的确切值只有通过适时测量才能确定。
于是基于此假设,加速度的谱密度函数就是
S
(
w
)
=
2
α
σ
2
(
w
2
+
α
2
)
S(w)= 2\alpha\sigma^2(w^2 +\alpha^2)
S(w)=2ασ2(w2+α2)
该假设通过Wiener-Kolmogorov白化过程进行处理可得关于加速度在状态空间的描述方式为
a
˙
(
t
)
=
−
α
a
(
t
)
+
w
(
t
)
\dot{a}(t)=-\alpha a(t) +w(t)
a˙(t)=−αa(t)+w(t)
其中:
w
(
t
)
w(t)
w(t)是均值为0,方差为
σ
2
\sigma^2
σ2的高斯白噪声。
2.1. Singer模型(连续)
令状态向量为
X
=
[
x
,
x
˙
,
x
¨
]
T
{X}=[x, \dot{x},\ddot{x}]^T
X=[x,x˙,x¨]T
则加速度为
a
(
t
)
=
x
¨
(
t
)
a(t)=\ddot{x}(t)
a(t)=x¨(t)
连续时间Singer模型为
X
˙
(
t
)
=
[
0
1
0
0
0
1
0
0
−
α
]
X
(
t
)
+
[
0
0
1
]
w
(
t
)
\dot{X}(t)=\begin{bmatrix}0&1&0\\0&0&1\\0&0&-\alpha\end{bmatrix}X(t) + \begin{bmatrix}0\\0\\1\end{bmatrix}w(t)
X˙(t)=⎣⎡00010001−α⎦⎤X(t)+⎣⎡001⎦⎤w(t)
Singer模型也可以表述为
X
˙
(
t
)
=
A
X
(
t
)
+
B
w
(
t
)
\dot{X}(t)=AX(t) + Bw(t)
X˙(t)=AX(t)+Bw(t)
其中
A
=
[
0
1
0
0
0
1
0
0
−
α
]
,
B
=
[
0
0
1
]
A=\begin{bmatrix}0&1&0\\0&0&1\\0&0&-\alpha\end{bmatrix}, B= \begin{bmatrix}0\\0\\1\end{bmatrix}
A=⎣⎡00010001−α⎦⎤,B=⎣⎡001⎦⎤
2.2. Singer模型(离散)
周期T采样离散化后,转化为离散时间状态方程为:
X
k
+
1
=
F
k
X
k
+
W
k
X_{k+1}=F_kX_{k} + W_k
Xk+1=FkXk+Wk
其中
F
k
=
[
1
T
(
α
T
−
1
+
e
−
α
T
)
/
α
2
0
1
(
1
−
e
−
α
T
)
/
α
0
0
−
e
−
α
T
]
F_k=\begin{bmatrix}1&T&(\alpha T-1+e^{-\alpha T})/\alpha^2\\0&1&(1-e^{-\alpha T})/\alpha\\0&0&-e^{-\alpha T}\end{bmatrix}
Fk=⎣⎡100T10(αT−1+e−αT)/α2(1−e−αT)/α−e−αT⎦⎤
噪声
W
k
W_k
Wk的方差为
Q
=
2
α
σ
2
[
q
11
q
12
q
13
q
21
q
22
q
23
q
31
q
32
q
33
]
Q=2\alpha \sigma^2 \begin{bmatrix}q_{11}&q_{12}&q_{13}\\q_{21}&q_{22}&q_{23}\\q_{31}&q_{32}&q_{33}\end{bmatrix}
Q=2ασ2⎣⎡q11q21q31q12q22q32q13q23q33⎦⎤
Q
Q
Q为对称矩阵,且

Singer模型还提出通过如下三重一致混合分布对加速度分布进行建模。
(1)目标可能以概率 P 0 P_0 P0无加速运动。
(2)目标或以等概率 P m a x P_{max} Pmax按最大或最小加速度 ( − + a m a x ) (-+a_{max}) (−+amax)运动。
(3)目标或者在区间 ( − a m a x , + a m a x ) (-a_{max}, +a_{max}) (−amax,+amax)按一致分布的加速度加、减速。于是基于该假设,计算可得加速度均值为零并且其方差为
σ 2 = a m a x 2 3 ( 1 + 4 P m a x − P 0 ) \sigma^2=\frac{a_{max}^2}{3}(1+4P_{max}-P_{0}) σ2=3amax2(1+4Pmax−P0)
式中, P m a x P_{max} Pmax、 P 0 P_0 P0 和 a m a x a_{max} amax 均为先验设计的参数。
上述模型可以推广到其他模型:
(1) 当时间常数 τ \tau τ较大,即 α \alpha α较小时,Singer模型趋于CA模型。
(2) 当时间常数 τ \tau τ较小,即 α \alpha α较大时,Singer模型趋于CV模型。
(3) Singer模型对目标机动模式的覆盖可以看作介于CV和CA模型之间。
3. 二维Singer模型
3.1. Singer模型(连续)
令状态向量为
X
=
[
x
,
x
˙
,
x
¨
,
y
,
y
˙
,
y
¨
]
T
{X}=[x, \dot{x},\ddot{x},y, \dot{y},\ddot{y}]^T
X=[x,x˙,x¨,y,y˙,y¨]T
则加速度为
a
(
t
)
=
[
x
¨
(
t
)
,
y
¨
(
t
)
]
T
a(t)=[\ddot{x}(t), \ddot{y}(t)]^T
a(t)=[x¨(t),y¨(t)]T
连续时间Singer模型为
X ˙ ( t ) = [ 0 1 0 0 0 0 0 0 1 0 0 0 0 0 − α 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 − α ] X ( t ) + [ 0 0 0 0 1 0 0 0 0 0 0 1 ] w ( t ) \dot{X}(t)=\begin{bmatrix}0&1&0&0&0&0\\0&0&1&0&0&0\\0&0&-\alpha&0&0&0 \\0&0&0&0 &1&0\\0&0&0&0 &0&1 \\0&0&0&0 &0&-\alpha \end{bmatrix} X(t) + \begin{bmatrix}0&0\\0&0\\1&0\\ 0&0\\0&0\\0&1\end{bmatrix}w(t) X˙(t)=⎣⎢⎢⎢⎢⎢⎢⎡00000010000001−α00000000000010000001−α⎦⎥⎥⎥⎥⎥⎥⎤X(t)+⎣⎢⎢⎢⎢⎢⎢⎡001000000001⎦⎥⎥⎥⎥⎥⎥⎤w(t)
为了方便,定义
A
=
[
0
1
0
0
0
1
0
0
−
α
]
,
B
=
[
0
0
1
]
A=\begin{bmatrix}0&1&0\\0&0&1\\0&0&-\alpha\end{bmatrix}, B= \begin{bmatrix}0\\0\\1\end{bmatrix}
A=⎣⎡00010001−α⎦⎤,B=⎣⎡001⎦⎤
则上式变为
X
˙
(
t
)
=
[
A
0
0
A
]
X
(
t
)
+
[
B
0
0
B
]
w
(
t
)
\dot{X}(t)=\begin{bmatrix}A&0\\0&A \end{bmatrix}X(t) + \begin{bmatrix}B&0\\0&B\end{bmatrix}w(t)
X˙(t)=[A00A]X(t)+[B00B]w(t)
3.2. Singer模型(离散)
周期T采样离散化后,转化为离散时间状态方程为:
X
k
+
1
=
F
k
X
k
+
W
k
X_{k+1}=F_kX_{k} + W_k
Xk+1=FkXk+Wk
其中
F
k
=
[
F
0
0
F
]
F_k=\begin{bmatrix}F&0\\0&F \end{bmatrix}
Fk=[F00F]
F = [ 1 T ( α T − 1 + e − α T ) / α 2 0 1 ( 1 − e − α T ) / α 0 0 − e − α T ] F=\begin{bmatrix}1&T&(\alpha T-1+e^{-\alpha T})/\alpha^2\\0&1&(1-e^{-\alpha T})/\alpha\\0&0&-e^{-\alpha T}\end{bmatrix} F=⎣⎡100T10(αT−1+e−αT)/α2(1−e−αT)/α−e−αT⎦⎤
噪声
W
k
W_k
Wk的方差为
Q
k
=
[
Q
0
0
Q
]
Q_k=\begin{bmatrix}Q&0\\0&Q \end{bmatrix}
Qk=[Q00Q]
Q
=
2
α
σ
2
[
q
11
q
12
q
13
q
21
q
22
q
23
q
31
q
32
q
33
]
Q=2\alpha \sigma^2 \begin{bmatrix}q_{11}&q_{12}&q_{13}\\q_{21}&q_{22}&q_{23}\\q_{31}&q_{32}&q_{33}\end{bmatrix}
Q=2ασ2⎣⎡q11q21q31q12q22q32q13q23q33⎦⎤
Q
Q
Q为对称矩阵,且

4. Singer模型matlab仿真
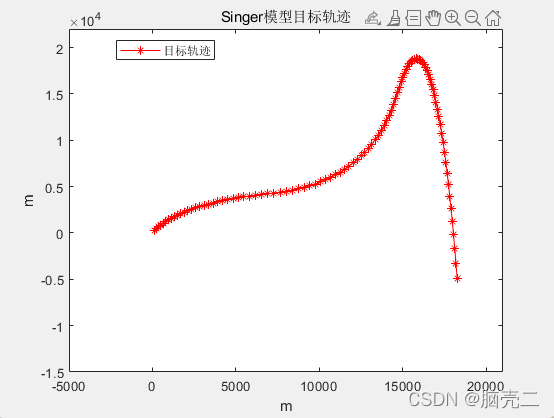
位置轨迹: 图1
速度轨迹: 图2
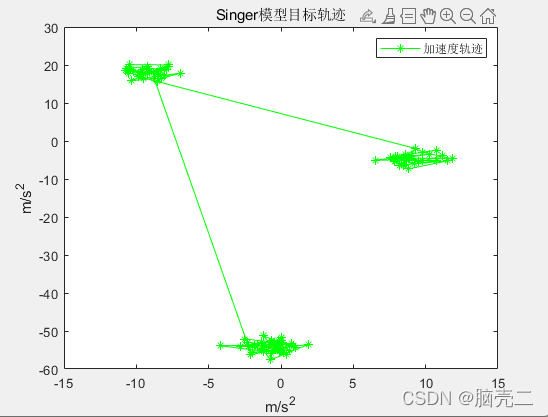
加速度轨迹: 图3

代码:
clear all; close all; clc;
%% initial parameter
n=6; %状态维数 ;
global T;
T=1; %采样时间
N=100; %运行总时刻
w_mu=zeros(6,1); % mean of process noise
v_mu=[0,0,]'; % mean of measurement noise
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Singer模型
%covariance of process noise
global a;% 定义全局变量
a= 0.1;% Singer 机动频率
% 方差计算
global sigma_q;
sigma_q= 3;
%------------------状态噪声协方差——
q11=(1-exp(-2*a*T) + 2*a*T + 2*a^3*T^3/3 - 2*a^2*T^2 - 4*a*T*exp(-a*T) )/(2*a^5);
q12=(exp(-2*a*T)+1-2*exp(-a*T)+2*a*T*exp(-a*T)-2*a*T+a^2*T^2)/(2*a^4);
q13=(1-exp(-2*a*T)-2*a*T*exp(-a*T))/(2*a^3);
q21=q12;
q22=(4*exp(-a*T)-3-exp(-2*a*T)+2*a*T)/(2*a^3);
q23=(exp(-2*a*T)+1-2*exp(-a*T))/(2*a^2);
q31=q13;
q32=q23;
q33=(1-exp(-2*a*T))/(2*a);
Q=2*a*sigma_q^2*[q11, q12, q13; q21, q22, q23; q31, q32, q33];
% % Q=blkdiag(Q,0.001);
Qk=blkdiag(Q,Q);
%%%%目标模型
F=[1 T (a*T-1+exp(-a*T))/a^2
0 1 (1-exp(-a*T))/a
0 0 exp(-a*T) ];
Fk=blkdiag(F,F);
% 初始状态的均值和方差
x=[0,100,10 0,200,-5 ]'; % 共8维,包括 x:位置 速度 加速度 加速度率; y:位置 速度 加速度 加速度率;
P_0=diag([1e3,10^2,10^1, 1e3,10^2,10^1]);
x0=mvnrnd(x,P_0); % 初始状态
%x0=(x+normrnd(0,0.001)')';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 目标航迹航迹生成
x=x0';
% 航迹生成
t1=30;
t2=60;
t3=100;
for k=1:1:t1
x(3)=10; x(6)=-5;
w=mvnrnd(w_mu',Qk)';
x=Fk*x + w;
sV(:,k,1)=x;
end
for k=t1+1:1:t2
x(3)=-10; x(6)=20;
w=mvnrnd(w_mu',Qk)';
x=Fk*x + w;
sV(:,k,1)=x;
end
for k=t2+1:1:t3
x(3)=-1; x(6)=-60;
w=mvnrnd(w_mu',Qk)';
x=Fk*x + w;
sV(:,k,1)=x;
end
figure
plot(sV(1,:,1),sV(4,:,1),'-*r')
xlabel('m');ylabel('m');
legend('目标轨迹')
title('Singer模型目标轨迹')
xlim([-5000,21000]); % 设置坐标轴范围
ylim([-15000,22000]);
figure
plot(sV(2,:,1),sV(5,:,1),'-*b')
xlabel('m/s');ylabel('m/s');
legend('速度轨迹')
title('Singer模型目标轨迹')
figure
plot(sV(3,:,1),sV(6,:,1),'-*g')
xlabel('m/s^2');ylabel('m/s^2');
legend('加速度轨迹')
title('Singer模型目标轨迹')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
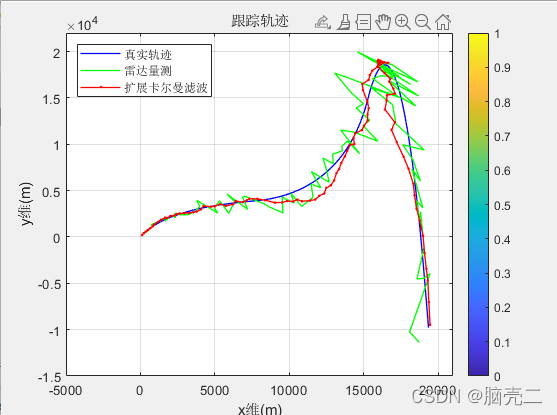
5. Singer模型扩展卡尔曼滤波EKF跟踪
跟踪轨迹如下:
RMSE曲线:
位置RMSE
速度RMSE


6. 其它模型
6.1 匀速转弯CT模型
匀速转弯CT运动模型见另一个博客:包括二维、三维
6.2. 匀加速运动CA模型
匀加速运动CA模型见另一个博客
6.3. “当前”统计模型
当前统计模型见另一个博客
6.4. Jerk统计模型
Jerk模型见另一个博客
==原创不易,路过的各位大佬请点个赞=


























 4708
4708

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










