逻辑回归 Logistic Regression
-
解决分类问题
-
通常做分类算法,只能作二分法
-
sigmod(x) = 1 / (1+e^-t)
# 直线型逻辑回归 from sklearn.linear_model import LogisticRegression log_reg = LogisticRegression() log_reg.fit(x_train, y_train) log_reg.score(x_test, y_test) # 多项式逻辑回归 from sklearn.preprocessing import PolynomialFeatures # 先使用poly处理x from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler log_reg_pipe = Pipeline([ ('poly', PolynomialFeatures(degree=2)), ('Standard', StandardScaler()), ('log_reg', LogisticRegression()) ]) log_reg_pipe.fit(x_train, y_train) log_reg_pipe.score(x_test, y_test)
分类准确度问题
- 对数据极度偏斜,只使用分类准确度远远不够
- 癌症的预测准确度为99.99%,但是只有0.01%的发病率,则对大多数人基本上不用预测都是健康的,预测机制几乎失灵
混淆矩阵 Confusion Matrix
- 行代表真实值,列代表预测值

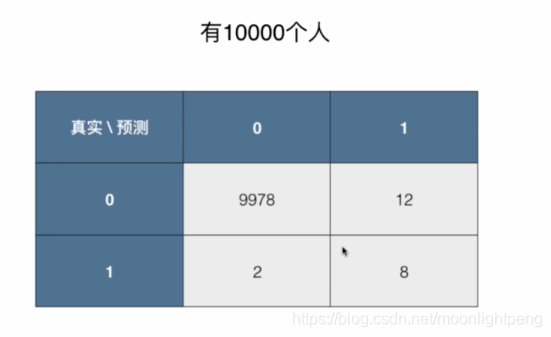
预测准确的有(0,0)(1,1),其余的都是预测错误的点
- 精准率:
precision = TP/ (TP + FP)只看对癌症预测成功或不成功的部分,而不对健康人群预测,健康人群的偏差过大 - 召回率:
recall = TP/ (TP + FN)对真实发生的癌症人群,能够发现的概率

from sklearn.metrics import confusion_matrix # 引入混淆矩阵
confusion_matrix(y_test, y_predict)
from sklearn.metrics import precision_score # 计算精准率
precision_score(y_test, y_predict)
from sklearn.metrics import recall_score # 计算召回率
recall_score(y_test, y_predict)
- 有时候我们会注重精准率:如股票预测
- 侧重召回率:病人诊断
调和平均值F1 Score

F1 = (2*precision * recall) / (precision + recall)
两个值如果有一个值偏小则整体偏小
两个都大时才大
对两个度量(精准率和召回率)的平衡计算
from sklearn.metrics import f1_score
f1_score(y_test, y_predict)
对数组值大于5的都变为1,小于5则为0
np.array(decision_scores >= 5, dtype='int')

Precision_Recall_Carve
- PR模型曲线更向外面积越大模型越好,
from sklearn.metrics import precision_recall_curve # 引入准确率和召回率的曲线函数
precision, recall, thresholds = precision_recall_curve(y_test, dec_fun) # 传入测试结果y_test和决策预测结果decision_function
print(precision.shape, recall.shape, thresholds.shape) # threshold比其余的小一,故绘图时需要precision[:-1]
import matplotlib.pyplot as plt
plt.plot(thresholds, precision[:-1], color='r') # 分别画出准确率和召回率的曲线
plt.plot(thresholds, recall[:-1], color='b')
plt.show()
plt.plot(recall, precision) # 画出准确率和召回率之间关系的曲线
plt.show()
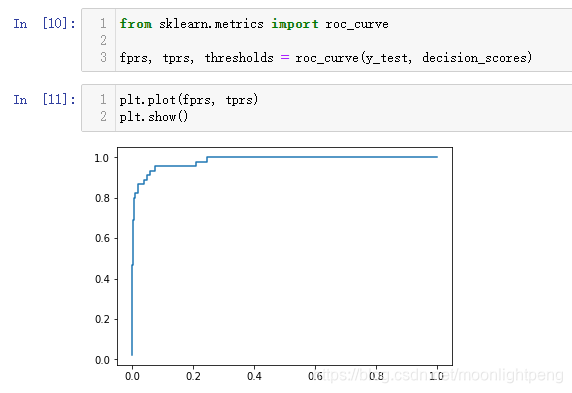
ROC
- TPR

- FPR

- 横轴为FPR, 纵轴为TPR,
plt.plot(fprs, tprs)
from sklearn.metrics import roc_curve
fprs, tprs, thresholds = roc_curve( y_test, dec_fun ) # 引入roc曲线
plt.plot(fprs, tprs) # 绘制roc曲线
plt.show()
from sklearn.metrics import roc_auc_score # 引入roc的曲线面积函数
roc_auc_score(y_test, dec_fun) # 求出roc曲线面积
多分类问题
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_predict) # 对分类问题中的混淆矩阵,此时y目标有多个特征值
























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








