第7章：OFDM 信道估计与均衡（5）

最新推荐文章于 2025-03-18 12:04:33 发布

通信陈老湿

最新推荐文章于 2025-03-18 12:04:33 发布

阅读量5.3k

点赞数 9

分类专栏：陈老湿·通信MATLAB仿真文章标签：数字通信数字信号处理

本文链接：https://blog.csdn.net/weixin_44283855/article/details/113955796

版权

陈老湿·通信MATLAB仿真专栏收录该内容

14 篇文章

订阅专栏

第7章（5）内容如下：

一、参考资料
二、OFDM相关问题继续探讨
三、CP和ZP对OFDM系统的影响（完整可运行MATLAB代码及其注意点）
四、总结

本已打算更新OFDM同步方面的内容了，但在这之前仍有许多问题浮现在脑海，比如

（1）保护间隔（GI）和循环前缀（CP）、补零（zero padding，ZP）的区别

（2）OFDM与IFFT、FFT的关系

（3）子载波（ICI）和符号间干扰（ISI）的区别

解决以上的问题，明晰一些概念，也是为OFDM同步的内容做知识储备。

我一直提到的《MIMO-OFDM无线通信技术及MATLAB实现》下载地址是：https://github.com/LyricYang/MIMO_OFDM，该书有的代码版本可能老旧，因此需要偶尔改改代码适应新的MATLAB版本才可以正常运行。

因此，本文先讨论以上提到的问题，然后集中在OFDM采用ZP或者CP，经过多径衰落信道的误码率分析，并附上完整可运行的代码，代码下载地址：123kevin456/OFDM-5。

若出现代码缺少子函数，可在《MIMO-OFDM无线通信技术及MATLAB实现》的下载地址中https://github.com/LyricYang/MIMO_OFDM 找到相应函数。

一、参考资料

1、《MIMO-OFDM的无线通信技术及其MATLAB实现》

2、孙宇彤《LTE教程：原理和实现》

此书对于刚开始接触LTE协议的我来说，有一定的帮助。该书没有复杂的计算公式，也没有代码的相关验证，用大量的例子和图示来通俗讲明白LTE协议的许多概念，不错。

3、CSDN的《OFDM专题之子载波间干扰问题（一）》和《OFDM专题之子载波间干扰问题（二）》、《给“小白”图示讲解OFDM的原理》，这几篇文章均不错，值得多次反复学习，我时不时会翻出来阅读，认真消化。

二、OFDM相关问题继续探讨

1、子载波干扰（ICI）和符号间干扰（ISI）是什么？出现这两种干扰后，各自的应对方法是什么？保护间隔（GI）和补零（ZP）、循环前缀（CP）的区别？

每次用到保护间隔时都是以CP的形式吗？用了CP后会有子载波干扰（ICI）和符号间干扰（ISI）吗？

2、IFFT与FFT等技术与OFDM实现的关系？OFDM是不是就一定要用到IFFT和FFT技术？或者更本质的讲，IFFT与FFT等技术在OFDM实现中，到底起到什么样的作用？

3、下图（a）中，为什么是不同子载波信号是加到一起再进行发送呢？而不是各自发送？这是受到什么约束了呢？

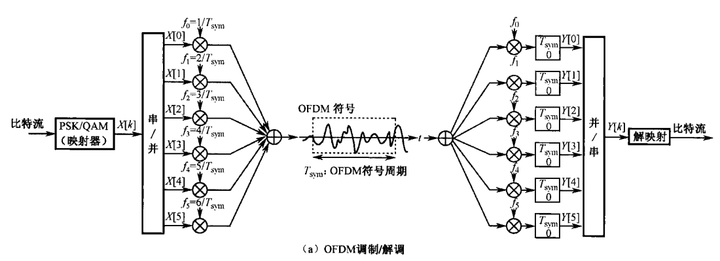
接下来对各个问题依次回答。

1、子载波干扰（ICI）和符号间干扰（ISI）是什么？出现这两种干扰后，各自的应对方法是什么？

在OFDM系统，最基本的传输单位是OFDM符号。由于同一信号的不同分量经过不同路径到达接收端的时间不一样。

如图4.14所示，如果保护间隔长度小于最大多径时延扩展，对于前一个OFDM符号的尾部已经影响到下一个OFDM符号的前端，这样就造成ISI。

有了符号间干扰怎么来解决呢？

当出现这个问题的时候，有的书籍便就立马引出来CP的概念了，但不解释清为什么。

其实有了符号间干扰后，我们的目的依然是让不同的OFDM符号区分开来，只需要加入保护间隔（GI）即可。

而保护间隔有两种插入方法，一种是补零（ZP），即在保护间隔中补充0。这便可以使得第n个符号经过最长路径后也不会影响到第n+1个符号，但这会给系统带来ICI。

（思考下为什么带来ICI？可以看《OFDM专题之子载波间干扰问题（一）》和《OFDM专题之子载波间干扰问题（二）》，这两篇文章解释得非常好）。

另一种便是CP。这个在《第7章：OFDM 信道估计与均衡（1）》中也已经讲到过其作用。

CP是既起到了保护间隔作用，避免了ISI，同时又使得循环扩展（为了某种连续性，可以说是为了循环卷积）消除了ICI，真是非常巧妙。

加CP和加ZP，对应在下面的代码中，是信号在接收端的处理方式有所不同。

function y=remove_GI(Ng,Lsym,NgType,ofdmSym)

if Ng~=0
  if NgType==1  % cyclic prefix
    y=ofdmSym(Ng+1:Lsym);
   elseif NgType==2 % zp
    y=ofdmSym(1:Lsym-Ng)+[ofdmSym(Lsym-Ng+1:Lsym) zeros(1,Lsym-2*Ng)];
  end
 else
  y=ofdmSym;
end

2、IFFT与FFT等技术与OFDM实现的关系？OFDM是不是就一定要用到IFFT和FFT技术？或者更本质地讲，IFFT与FFT等技术在OFDM实现中，到底起到什么样的作用？

在实现OFDM时，IFFT和FFT不是唯一的方法，但是一种比较好的方法。

孙宇彤《LTE教程：原理和实现》还介绍了OFDM信号的其他生成算法，比如反向离散哈特利变换（IDHT）、离散余弦变换等等。

接下来再举孙宇彤《LTE教程：原理和实现》中讲到IFFT作用，这与我在别的地方看到的不一样，可做参考。

三、CP和ZP对OFDM系统的影响（完整可运行MATLAB代码及其注意点）

%%%%%%%%%%%%%%%%%%%%%       检查正弦信号间的相交性    %%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%        OFDM_basic_myself3.m            %%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%      data:2020年12月11日  author:飞蓬大将军 %%%%%%%%%%

%%%%%%%%%%%%%%%%%程序说明
%%%（1）CP和ZP作用   （2）子载波干扰与符号间干扰的区别及其消除方法

%%%%%%    仿真环境
%软件版本：MATLAB R2019a

%**************************** 程序主体 **************************%
clear all;

%%%%%%%%%%%%%%%%%%%%参数设定%%%%%%%%%%%%%


%%%%选择CP或ZP
NgType = 1;  %对于ZP或CP NgType = 1或2
if NgType == 1
    nt = 'CP';
elseif NgType == 2
    nt = 'ZP';
end

%%%%选择信道类型
Ch = 0;
if Ch == 0
    chType ='AWGN'; %高斯白噪声信道 
    Target_neb = 100;
else
    chType ='CH';
    Target_neb = 500;
end
figure(Ch+1);
clf;

PowerdB = [0 -8 -17 -21 -25]; %信道抽头功率特性'dB'
Delay = [0 3 5 6 8]; %信道时延 
Power = 10.^(PowerdB/10); %信道抽头功率特性 '线性'
Ntap = length(PowerdB);
Lch = Delay(end)+1;
Nbps = 2;   %调制阶数 2/4/6
M = 2^Nbps; %QPSK、16-QAM、64-QAM
Nfft = 64; %FFT大小

%Ng = 3;

Ng = Nfft/4; %保护间隔（GI）长度，若没有保护间隔，Ng = 0
Nsym = Nfft + Ng; %符号周期

%%%调整Nvc
Nvc = Nfft/4; %Nvc若等于0，则没有VC（虚拟子载波）
% Nvc = 0; %Nvc若等于0，则没有VC（虚拟子载波）

Nused = Nfft - Nvc; %Nused为用于传输数据的子载波数

EbN0 = [0:2:20];  %Eb/N0
% EbN0 = 50;  %Eb/N0
N_iter = 1e5;  %对于每一次EbN0的迭代次数
Nframe = 3; %每一帧的符号数
sigPow = 0; %初始信号功率
file_name = ['OFDM_BER_' chType '_' nt '_' 'GL' num2str(Ng) '.dat'];
fid = fopen(file_name,'w+');
norms = [1 sqrt(2) 0 sqrt(10) 0 sqrt(42)];  %BPSK 4-QAM 16-QAM


for i = 0:length(EbN0)
    randn('state',0);
    rand('state',0);
    Ber2=ber(); %初始化BER
    Neb = 0; %初始化误比特数
    Ntb = 0; %初始化总比特数
    for m = 1:N_iter
        X = randi([0 M-1],1,Nused*Nframe);
        Xmod = qammod(X,M,'gray')/norms(Nbps);
        if NgType~=2
            x_GI = zeros(1,Nframe*Nsym);
        elseif  NgType == 2
            x_GI = zeros(1,Nframe*Nsym+Ng);
        end
%         kk1 = 1:Nused/2;
%         kk2 = Nused/2+1:Nused;
        kk1 = [1:Nused/2];
        kk2 = [Nused/2+1:Nused];
        kk3 = 1:Nfft;
        kk4 = 1:Nsym;
        for k = 1:Nframe
            if Nvc~= 0
                X_shift = [0 Xmod(kk2) zeros(1,Nvc-1) Xmod(kk1)];
            else
                X_shift = [Xmod(kk2) Xmod(kk1)];
            end
            x = ifft(X_shift);
            x_GI(kk4) = guard_interval(Ng,Nfft,NgType,x);
            kk1 = kk1 + Nused;
            kk2 = kk2 + Nused;
            kk3 = kk3 + Nfft;
            kk4 = kk4 + Nsym;
        end
        
        %%%%%能量检测
        if i == 0   %只测量信号功率
            sigPow_temp = x_GI*x_GI';;
        end
        
        
        
        if Ch==0
            y = x_GI;  %没有信道
        else      %多径衰落信道
            channel =(randn(1,Ntap)+1j*randn(1,Ntap)).*sqrt(Power/2);
            h = zeros(1,Lch);
            h(Delay+1) = channel;
            y = conv(x_GI,h);
        end
        
        if i == 0   %只测量信号功率
            y1 = y(1:Nframe*Nsym);
            sigPow = sigPow + y1*y1';
            continue;
        end

        %******************** 信道 ***********************%
        snr = EbN0(i) + 10*log10(Nbps*(Nused/Nfft));  %%方便fig标号，（1）,原书公式
%         snr = EbN0(i) + 10*log10(Nbps);
%         snr = EbN0(i) + 10*log10(Nbps*(Nfft/Nsym));  %%方便fig标号，（3）CP消耗能量
        noise_msg = sqrt((10.^(-snr/10))*sigPow/2);
        y_GI = y + noise_msg*(randn(size(y)) + 1j*randn(size(y)));
        
        %%%%%%%%%%%接收端
        kk1 = (NgType==2)*Ng + [1:Nsym];
        kk2 = 1:Nfft;
        kk3 = 1:Nused;
        kk4 = Nused/2 + Nvc + 1:Nfft;
        kk5 = (Nvc~=0)+[1:Nused/2];
        if Ch ==1
            H = fft([h zeros(1,Nfft-Lch)]);  %信道频率响应
            H_shift(kk3) = [H(kk4) H(kk5)];
        end
        
        for k =1:Nframe
            Y(kk2) = fft(remove_GI(Ng,Nsym,NgType,y_GI(kk1)));
            Y_shift = [Y(kk4) Y(kk5)];
            if Ch ==0
                Xmod_r(kk3) = Y_shift;
            else
                Xmod_r(kk3) = Y_shift./H_shift;  %均衡器
            end
            kk1 = kk1 + Nsym;
            kk2 = kk2 + Nfft;
            kk3 = kk3 + Nused;
            kk4 = kk4 + Nfft;
            kk5 = kk5 + Nfft;
        end
        X_r = qamdemod(Xmod_r*norms(Nbps),M,'gray');
        Neb = Neb + sum(sum(de2bi(X_r,Nbps)~=de2bi(X,Nbps)));
        Ntb = Ntb + Nused*Nframe*Nbps;
%         if Neb>Target_neb
%             break
%         end
    end
    if i == 0
        sigPow = sigPow/Nsym/Nframe/N_iter;
        fprintf('Signal power= %11.3e\n', sigPow);
        fprintf(fid,'%%Signal power= %11.3e\n%%EbN0[dB]       BER\n', sigPow);
    else
        Ber = Neb/Ntb;
        fprintf('EbN0=%3d[dB], BER=%4d/%8d=%11.3e\n', EbN0(i), Neb,Ntb,Ber)
        fprintf(fid, '%d\t%11.3e\n', EbN0(i), Ber);
        if Ber<1e-6
            break;
        end
    end
end %end for i
if(fid~=0)
     fclose(fid);
end
disp('sumualtion is finished');
plot_ber(file_name,Nbps);

%%%%选择CP或ZP
if Ch == 1
    if NgType == 1
        a = load(file_name);
        save('ofdm_basic_myself3_cp16_rayleigh','a');
    elseif NgType == 2
        b = load(file_name);
        save('ofdm_basic_myself3_zp16_rayleigh','b');
    end
else
    

%%%%%%%%%%%%%%实验记录
%%%%2020年12月11日
%%%%CP和ZP都能起到保护间隔的作用，消除了子载波干扰和符号间干扰
%%%%在AWGN和瑞利信道下均能画出正确误码率曲线

在上面的代码中，有以下几点值得注意：

（1）SNR其实是ES/N0

原书公式snr = EbN0(i) + 10log10(Nbps）+10log10*(Nused/Nfft))，其实是EsN0（i） = EbN0(i) + 10log10(Nbps）+10log10*(Nused/Nfft)) 有10*log10(Nbps）这一项是很好理解的，因为一个调制后的符号能量是Nbps个比特的能量。后面的10*log10*(Nused/Nfft))让我想了非常久。

由 ${E_b}{R_b} = {E_s}{R_s}$ ，得到 $\frac{{{E_s}}}{{{N_0}}} = \frac{{{E_b}}}{{{N_0}}}\frac{{{R_b}}}{{{R_s}}}$ 。