第五十七章 解读轮盘赌算法

基础解读

轮盘赌算法的基本思想是：各个个体被选中的概率与其适应度函数值大小成正比，它是为了防止适应度数值较小的个体被直接淘汰而提出的。
为了弄清轮盘赌算法，我搜集了相关的文献和教材，发现很多文章都喜欢把轮盘赌算法与遗传算法、蚁群算法、蜂群算法等混入一起来解释，这样轮盘赌算法中就会冒出什么染色体、遗传下一代、信息正反馈、信息素、雇佣蜂等词语，看起来“高大上”，这样也使得简单实用的轮盘赌算法在理解和实现上都变得复杂。话说，轮盘赌算法是可以应用到遗传算法、蚁群算法中去，但其算法的机理和遗传算法、蚁群算法是相互独立的，它的实现机理和遗传算法、蚁群算法、蜂群算法等没有任何关系，也没有什么染色体、遗传下一代、信息正反馈等高大上的词汇。
轮盘赌算法的核心在于两个概率和个体选择策略：
（1）个体选择概率
（2）累积概率
（3）如何选择某个个体
1、个体个体选择概率比较好理解，适应度数值越高，它被选中的概率就越大，使用以下公式来表示。

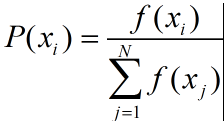
其中，xi为某个个体。
2、累积概率把各个个体的概率使用不同长度的线段来表示，这些线段组合成一条直线，直线的长度为1（各个个体概率之和），这样在该直线中，某段的线段最长，就代表该个体被选中的概率越大。它的机理为：
（一）任意选择所有个体的一个排列序列（这个序列可以随便排，因为是某线段之间的长度为代表某个体的选择概率）
（二）任意个体的累积概率为该个体对应的前几项数据的累加和。
某个个体的累加概率公式如下：

这样，如果某个个体的适应度数值高，它所对应的个体选择概率就会越大，通过累积概率转换后对应的线段会越长。

3、选择某个个体策略为在区间[0 1]中随机产生一个数，看看该数字落在那个区间，很明显，对于适应度值较大的个体，对应的线段长度会长，这样随机产生的数字落在此区间的概率就大，该个体被选中的概率也大。同时，对于适应度较小的个体，线段长度会相对较短，随机数字在该区间的概率相对较小，但是也有被选中的可能，避免了适应度数值较小的个体被直接淘汰的问题。
综上，轮盘赌算法的实现步骤为
（i）初始化各个个体的适应度值（适应度值就是某个数值，什么数据都可以，只是对于不同的问题，这个适应度值代表的意义不一样）
（ii）根据公式计算各个个体的个体选择概率和累积概率
（iii)在区间[0 1]之间随机生成一个数，判断该数落在哪个区间内，如果落在某个区间，则该区间被选中。
例子：使用轮盘赌算法根据各个个体被选中的概率与其适应度函数值大小成正比原理，使用了[0.23 0.65 0.38 0.96 0.14 0.76 0.99 0.76 0.56 0.77];%10个模拟适应度值做了实验，计算了3次，每次循环100次。根据算法思想应该为适应度值越大，该个体被选择的概率也就越大，也就是说这100次中该个体被选中的次数应该越多。
第一次： 3 8 8 16 3 17 19 9 3 14
第二次： 2 10 8 15 1 8 18 12 11 15
第三次： 4 15 3 19 6 8 14 13 9 9
可以看到，对于适应度值为0.14的个体，这3次中选中的次数分别为：3、1、6，而对于适应度为0.99的个体，这3次中选中的次数分别为：19,18，14。基本满足了轮盘赌算法的原理。

轮盘赌算法原理与实现

轮盘赌选择法（roulette wheel selection）是最简单也是最常用的选择方法，在该方法中，各个个体的选择概率和其适应度值成比例，适应度越大，选中概率也越大。但实际在进行轮盘赌选择时个体的选择往往不是依据个体的选择概率，而是根据“累积概率”来进行选择。

轮盘赌选择法操作过程

以一个实例来讲述轮盘赌选择法的具体过程，现有一个抽奖轮盘如下：

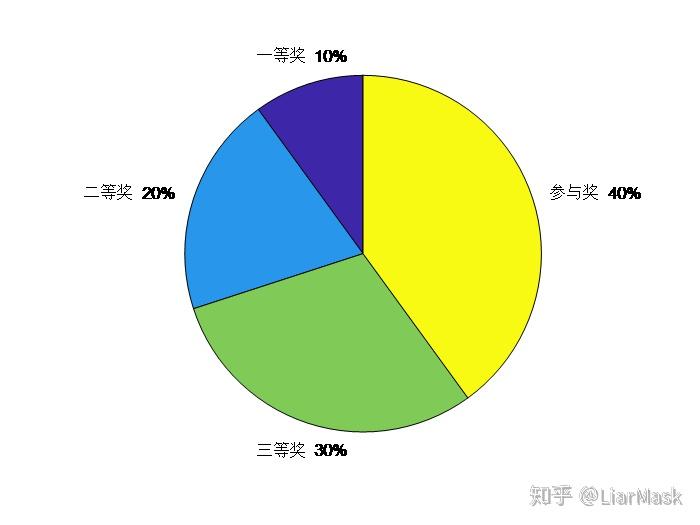
抽奖轮盘

显然，当我们直接转动轮盘时抽到“参与奖”的概率最大，因为它占总体的比例最高，这也体现了“轮盘赌选择法”中所占比例越大被选中概率越高的思想。但我们一般不采用抽中“几等奖”的概率这种定性的指标来表述每个部分被选中的概率，而是引入“适应度”与“累积概率”的概念，其中每个部分被选中的概率与其适应度值成比例。设某一部分x(i)的适应度值表示为$f(xi)$，该部分被选中的概率为$p(xi)$，累积概率为$q(xi)$。

累积概率表示每个个体之前所有个体的选择概率之和，它相当于在转盘上的“跨度”，“跨度”越大越容易选到，就相当于概率论中的概率分布函数F(x)。轮盘赌选择法的过程如下：

（1）计算每个个体的被选中概率$p(xi)$

（2）计算每个部分的累积概率$q(xi)$

（3）随机生成一个数组m，数组中的元素取值范围在0和1之间，并将其按从小到大的方式进行排序。若累积概率$q(xi)$大于数组中的元素$m[i]$，则个体$x(i)$被选中，若小于$m[i]$，则比较下一个个体$x(i+1)$直至选出一个个体为止。

（4）若需要转中N个个体，则将步骤（3）重复N次即可

看了上面的选择过程我们可能有这样的疑问：由于个体的选择是以“累积概率”为标准的，但一个个体的累积概率$q(xi)$大并不表示它的选中$p(xi)$也大，因为根据q(xi)的计算公式我们知道累积概率表示的是每个个体之前所有个体的选择概率之和，这难道不会导致某些个体明明选中概率很小但却因为它位置靠后而导致其累积概率很大而被选中的情况发生吗？显然这与轮盘赌选择法的初衷是矛盾的啊！

为了验证上述情况是否会发生，以上面的“轮盘抽奖游戏”为例，给每个奖项给定一个编号，编号的数字代表了他在总体中的位置，如下：

由表格可以看到：“一等奖”的选中概率最小，但却因为其编号最大导致其累积概率为1，那是否会出现一等奖百分比会被选中的事件出现呢？为了验证结果，进行实验。进行1000次轮盘抽奖，并记录每次抽奖的编号，得到结果如下表所示:

从最终的结果可以看出，采用累积概率的方式并没有出现“抽中一等奖”事件的概率很大的结果，反而最终的结果和每个奖项的选中概率相近，这说明采用累积概率的轮盘赌选择法是切实可行的，且其选择结果误差很小。

附上代码

import numpy as np

# 初始化奖项对应的适应度值
fitvalue = np.array([4, 3, 2, 1])

# 计算适应度总和
totalf = np.sum(fitvalue)

# 计算每个个体被选中的概率
p = fitvalue / totalf

# 计算每个个体的累积概率
q = np.cumsum(p)

# 初始化用于存放各奖项被选中次数的计数器
c1 = c2 = c3 = c4 = 0

# 进行抽奖，直到总抽选次数达到996次
while c1 + c2 + c3 + c4 <= 996:
    fitin = 0
    newin = 0
    m = np.sort(np.random.rand(4))  # 生成一组从小到大排列的随机数组

    while newin < 4:
        if q[fitin] > m[newin]:
            selected = fitin + 1
            # 根据选中的编号增加对应奖项的计数
            if selected == 1:
                c1 += 1
            elif selected == 2:
                c2 += 1
            elif selected == 3:
                c3 += 1
            elif selected == 4:
                c4 += 1
            newin += 1
        else:
            fitin += 1

# 计算每个奖项被选中的概率
pc1 = c1 / (c1 + c2 + c3 + c4)
pc2 = c2 / (c1 + c2 + c3 + c4)
pc3 = c3 / (c1 + c2 + c3 + c4)
pc4 = c4 / (c1 + c2 + c3 + c4)

# 显示结果
print('***************************************')
print(f'抽中“参与奖”的次数为：{c1}')
print(f'抽中“参与奖”的概率为：{pc1}')
print('***************************************')
print(f'抽中“三等奖”的次数为：{c2}')
print(f'抽中“三等奖”的概率为：{pc2}')
print('***************************************')
print(f'抽中“二等奖”的次数为：{c3}')
print(f'抽中“二等奖”的概率为：{pc3}')
print('***************************************')
print(f'抽中“一等奖”的次数为：{c4}')
print(f'抽中“一等奖”的概率为：{pc4}')
print('***************************************')