【数学建模】排队论

A 排队论简介

排队论又称随机服务系统，是研究系统随机聚散现象和随机 服务系统工作过程的数学理论和方法，是运筹学的一个分支。
现实生活中如排队买票、病人排队就诊、轮船进港、高速路 上汽车排队通过收费站、机器等待修理等都属于排队论问题。

定义：

• 通过对服务对象到来及服务时间的统计研究（输入服务对象什么时候来，服从什么样的分布，服务的时间长度服从什么样的分布）；
• 根据分布得出数量指标【等待时间、排队长度、忙期长短（空闲与运营的时间长度，可通过增减服务台数量来优化）等，通常优化的就是等待时间】的 统计规律；
• 然后根据这些规律来改进服务系统的结构(改变服务台数量)或重新组织被服务对象（如登飞机时，让靠窗户的人先进，残疾的人弄一个特殊通道）
• 使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优。

B 模型建立

B.a 排队论基本构成与指标

1 排队论的基本构成
输入过程：描述顾客按照怎样的规律到达排队系统。顾客总体（有限/无限）、到达的类型（单个/成批）、到达时间间隔服从什么分布。
排队规则：指顾客按怎样的规定次序接受服务。常见的有等待制（我来了一定要等到我被服务）、损失制（我发现这里人很多我就走了）、混合制、闭合制。
服务机构：服务台的数量; 服务时间服从的分布。

2 排队系统的数量指标
队长：系统中的平均顾客数（包括正在接受服务的顾客）。
等待队长：系统中处于等待的顾客的数量（不包括正在接受服务的顾客）。
等待时间：等待时间包括顾客的平均逗留时间。
忙期：连续保持服务的时长。

B.b 数学表示

1 排队论中的符号表示
$$A/B/C/n$$
A 输入过程，B 服务时间，C 服务台数，n 系统容量。
如：$$M/M/S/\infty$$

• 输入过程是 Poisson 流
• 服务时间服从负指数分布
• 系统有 S 个服务台平行服务
• 系统容量为无穷大的等待制排队系统(可以排无限长的队)

2 等待制模型$M/M/S/\infty$

• 顾客到达规律服从参数为 λ 的 Poisson 分布 :
  P { X ( t ) = k } = ( λ t ) k e − λ t k ! P\{X(t)=k\}=\frac{(\lambda t)^ke^{-\lambda t}}{k!} P{X(t)=k}=k!(λt)ke−λt​
  表示0到t时刻，到达的顾客数等于k的概率。单位时间到达的顾客平均数为$\lambda$，所以[0,t]时间内到达的顾客平均数为$\lambda t$

• 顾客接受服务的时间服从参数为 µ 的负指数分布
  $$f(t)=\mu e^{-\mu t}(t>0)$$
  $\mu$是单位时间所能服务的人数
  每个顾客接受服务的平均时间为$1/\mu$

(1) 等待制度模型$M/M/S/\infty :S=1$(单服务台)

• 系统的服务强度 & 无顾客的概率 & 有 n 个顾客的概率：
  

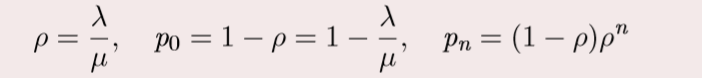
• 平均队长：
  

• 平均等待队长
  

• 平均逗留时间：
  

• 平均等待时间
  

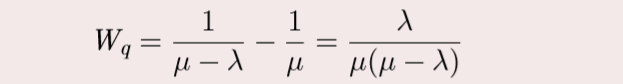
• Little 公式
  $L_s为平均队长；L_q是到访人员平均等待队长$
  
  

(1) 等待制度模型$M/M/S/\infty :S>1$(多服务台)
服务能力和强度

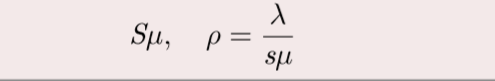
服务台都空闲的概率

平均队长

平均逗留时间

平均等待时间

平均等待队

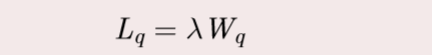
lambda=20;
mu=9;
s=3;  % 1*9=9<20；2*9=18<20
rho=lambda/(s*mu);
p0=0;
for k=1:s-1
    p0=p0+sum(s*rho).^k./factorial(k);
end
p0=1./(p0+(s*rho)^s*rho/(factorial(s)*(1-rho)));
Ls=s*rho+(s*rho)^s*rho/(factorial(s)*(1-rho)^2)*p0;
Ws=Ls/lambda;
Wq=Ws-1/mu;   %单位：小时

3 其它模型

混合制：容量就是队长的最大长度
闭合制：工厂的几个工人负责几个机器，把机器看成顾客，即机器即是容量，也是顾客。

4 实际模拟
开始服务, 到达, 离开时刻和服务, 等待时长的关系：

• 单服务台

到达时刻：可以用一种分布生成一定间隔的时间序列。
服务时刻：
1） 上一个人还没离开则取决于他离开的时刻
2） 上一个人已经离开则取决于下一个人到达的时刻。

• 多服务台

k是最先空闲的服务台
第四行：k空闲的时刻就是第$i$个人离开的时刻。
自动取款机问题

单服务台

n = 100000;             % 模拟顾客总数
mu = 1;                 %到达率，平均每分钟到达 1 位
muA = 0.9;              % 服务率，的平均服务时间为 0.9,
tarr = cumsum(exprnd(mu,1,n)); % 到达时刻：生成一个服从指数分布的时间间隔并累加
tsrv = exprnd(muA,1,n);        %服务时长
tsta = zeros(1,n);             % 初始化服务时刻
tlea = zeros(1,n);             % 初始化离开时刻
twat = zeros(1,n);             % 初始化等待时长
tsta(1) = tarr(1);             % 首位顾客服务时刻=到达时刻
tlea(1) = tsta(1) + tsrv(1);   % 首位顾客离开时刻=到达时刻+服务时刻
twtime(1) = tlea(1) - tarr(1); % 首位顾客等待时长=离开时刻-到达时刻
for i = 2:n        % 从第二个人
    % 服务时刻=max{到达时刻，上一个顾客离开时刻}
    tsta(i) = max(tarr(i),tlea(i-1)); 
    % 离开时刻=服务时刻+服务时长
    tlea(i) = tsta(i) + tsrv(i);       
    % 等待时长=离开时刻-到达时刻
    twat(i) = tlea(i) - tarr(i);
end
hist(twat)    % 逗留时间分布
sum(twat)/n   % 逗留时间平均值

双服务台

n = 100000; 
mu = 1; muB = 1.8;
tarr = cumsum(exprnd(mu,1,n));
tsrv = exprnd(muB,1,n);
tsta = zeros(1,n);
tlea = zeros(1,n);
twat = zeros(1,n);
last = [0 0];     % 初始化服务台结束服务时刻，多个服务台只需加多几个0即可
for i = 2:n
    [minemp, k] = min(last);  %找出最快结束服务的服务台时刻
    tsta(i) = max(tarr(i),minemp); % 服务时刻
    tlea(i) = tsta(i) + tsrv(i);   % 离开时刻
    last(k) = tlea(i);             % 服务台结束服务时刻
    twat(i) = tlea(i) - tarr(i);   % 等待时长
end
hist(twat)
sum(twat)/n

C 案例

题目出现等待时间以及队长，则很有可能是排队论问题。
1银行服务问题

R(R<0.8)：这时R小于0.5的已经变成2了。

%% 计算到达的时刻以及服务的时长
n = 150; 
ta = [5 4 3 2 1 0]; 
pa = [0.05 0.25 0.35 0.10 0.15 0.10]; 
ts = [ 4 3 2 1 ]; 
ps = [ 0.15 0.40 0.20 0.25 ]; 
pacum = cumsum(pa); 
pscum = cumsum(ps);
Tarrival = rand(1,n); 
for i = 1:length(pa)
 Tarrival(Tarrival<pacum(i)) = ta(i); 
end
Tarrival = cumsum(Tarrival);  % 到达时刻
Tservice = rand(1,n);         % 服务时长
for i = 1:length(ps)
    Tservice(Tservice<pscum(i)) = ts(i); 
end
%% 计算队长，平均等待时间
Tstart = zeros(1,n); %开始服务的时刻
Tleave = zeros(1,n); %离开的时刻
Twait = zeros(1,n);  %等待的时长
line = zeros(1,n);   %队长度
Tstart(1) = Tarrival(1); %第一个人开始服务的时刻等于到达的时刻
Tleave(1) = Tstart(1) + Tservice(1); 
Twait(1) = Tleave(1) - Tarrival(1) - Tservice(1); %等待的时长=离开的时刻-到达的时刻-服务的时刻 
line(1) = 0;   % 排在第一人之前的人为0.
for i = 2:n 
    Tstart(i) = max(Tleave(i-1), Tarrival(i)); 
    Tleave(i) = Tstart(i) + Tservice(i);   % 离开的时刻=开始服务的时时长+服务的时长
    Twait(i) = Tleave(i) - Tarrival(i) - Tservice(i);
    %队长计算
    k = i-1;   % i前面的人
    while ( k>0 )&&( Tarrival(i)<Tleave(k) )  %i到了k还没离开=k还在队伍里
        line(i) = line(i) + 1; 
         k = k - 1;                           % 再依次判断k-1在不在队列中
    end
end

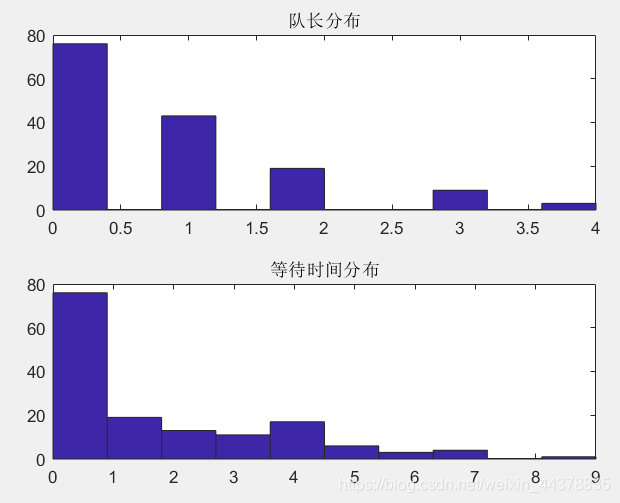
2 优化机场安检口旅客通行

混合串并连系统：左边为登记服务台，蓝色为普通的，红色为VIP。
右边绿色为过安检的服务台。

function [tlea, twat, qlen] = mms(tarr, type, mus)
% 输入：每个人到达的时刻；这个人的类型；服务效率
narr = length(tarr);        % 顾客数目
nsvr = length(mus);         % 服务台数目
last = zeros(nsvr,1);        % 服务台结束服务的时刻
[tsta, tlea, twat, qlen] = deal(zeros(narr,1)); % deal：全部复制为zeros(narr,1)
% 生成每个人服务的时间长度
rndm = zeros(nsvr,narr);  
for k = 1:nsvr; rndm(k,:) = exprnd(mus(k)*type); end
for i = 1:narr
    % find booth service was/will be emptied soonest and record
    [minemp, ksvr(i)] = min(last); 
    % start time = max{arrival time, minemp}
    tsta(i) = max(tarr(i), minemp); 
    % severe time = exponential random number with mean parameter mu
    tsvr(i) = rndm(ksvr(i),i);
    % leaving time = start time + service time
    tlea(i) = tsta(i) + tsvr(i);
    % last time of k-th server = leaving time of i-th customer 
    last(ksvr(i)) = tlea(i);
    % waiting time = leaving time - arrival time
    twat(i) = tlea(i) - tarr(i);
    % queue length for i customer
    j = i - 1;
    while j>0 && tarr(i)<tlea(j)
        if ksvr(j)==ksvr(i); qlen(i) = qlen(i) + 1; end
        j = j - 1;
    end
end

% 服务台数量
n1 = 2; n2 = 3; n3 = 3;
% 到达率
mu1 = 12; mu2 = 9; mu3 = 16;
% 服务率
muR = 10; muB = 13;
%服务人数
nR = ceil(24*3600/muR); nB = ceil(24*3600/muB);
%蓝色和红色到达的时刻
tArrR = cumsum(exprnd(muR,nR,1));
tArrB = cumsum(exprnd(muB,nB,1)); 
tArr = [tArrR; tArrB];
% VIP和非VIP，VIP服务（通过）时间短
type = [0.8*ones(nR,1); 1.2*ones(nB,1)];
%红色服务台输出
[tLeaR, tWatR, qLenR] = mms(tArrR, ones(nR,1), mu1*ones(n1,1));
%蓝色服务台输出
[tLeaB, tWatB, qLenB] = mms(tArrB, ones(nB,1), mu2*ones(n2,1));
% 红色和蓝色离开时刻总的进行排序
[tArrG, order] = sort([tLeaR; tLeaB]);
[tLeaG, tWatG, qLenG] = mms(tArrG, type(order), mu3*ones(n3,1));
tLeaG(order) = tLeaG;
tWatG(order) = tWatG;
qLenG(order) = qLenG;
figure('position',[50,50,1200,600])
subplot(2,3,1); hist(qLenR); ylabel('Frequency'); 
xlabel('length of the waiting line'); title('Red')
subplot(2,3,4); hist(tWatR); ylabel('Frequency'); 
xlabel('waiting time'); title('Red')
subplot(2,3,2); hist(qLenB); ylabel('Frequency');
xlabel('length of the waiting line'); title('Blue')
subplot(2,3,5); hist(tWatB); ylabel('Frequency'); 
xlabel('waiting time'); title('Blue')
subplot(2,3,3); hist(qLenG); ylabel('Frequency');
xlabel('length of the waiting line'); title('Green')
subplot(2,3,6); hist(tWatG); ylabel('Frequency'); 
xlabel('waiting time'); title('Green')