深度学习中的卷积操作

在查看卷积网络代码时，发现了各种不同的卷积操作，所以查找了一篇论文，并将其分享在这里，希望通过这篇论文对卷积操作有更加全面和系统的认识。
论文名称：A guide to convolution arithmetic for deep learning

引言

离散卷积（Discrete convolutions）

神经网络的基本原理是仿射变换：一个向量作为输入并且与一个矩阵相乘得到输出（在将结果传入非线性系统之前通常会为其添加一个偏置项），这种操作适用于图像，声音或者无序的特征集合等类型的输入，无论他们有几个维度，都可以在转换之前展开成为一个向量。
图像、声音等类似的数据类型享有某些共同的属性：
1.他们都是多维数组
2.他们都具有一个或多个轴，例如图像的长宽，声音的时间轴，并且这些轴的顺序很重要。
3.他们都有一个轴是通道轴（channel），这个轴用于访问数据的不同层次，例如彩色图像的RGB通道，声音数据的左右声道。
当应用仿射变换时，不利用这些属性，所有的轴都以同样的方式处理，拓扑信息没有被考虑在内。不过，利用数据的隐式结构可能在解决某些任务时非常方便，如计算机视觉和语音识别，在这些情况下，最好可以保留这些信息。这就是离散卷积发挥作用的地方。
离散卷积是一种线性变换，这种变换保留了顺序信息。这种卷积是稀疏的（只有少部分的输入单元对给定输出单元有贡献）并且是权值共享的（相同的权重会被应用在输入数据的多个位置）。

下图是一个33卷积核对一个55的数组进行卷积的示意图，卷积核移动的方向是从左往右，从上到下，步长为1：

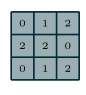
下图是带有padding的卷积操作：
维度为2（$N=2$），特征图的长宽均为5($i_1=i_2=5$)，卷积核的长宽均为3($k_1=k_2=3$)，卷积核在长轴和宽轴上移动的步长都是2($s_1=s_2=2$)，填充（padding）大小为1($p_1=p_2=1$)。

卷积核在输入特征图上滑动，在每个位置，计算卷积核的每个元素和与之重叠的输入特征图上的元素之间的乘积，再求和即可获得当前位置的输出。可以通过使用不同的卷积核重复这一过程来产生所需数量的输出特征图（即在训练过程中卷积操作的输出通道数）。如果有多个输入特征图，则卷积核需要是三维的——或者，等效地，每个特征图都要与不同的核卷积——并且所产生的特征图将被按元素求和以产生输出特征图。
下图是两个输入特征图，使用一个$3\ast 2\ast 3\ast 3$的卷积集合（3个不同的卷积，卷积核尺寸为$(2\ast 3\ast 3)$）生成三个不同的特征图，这三个特征图中分别包含了两个子特征图，最终生成的特征图是每个特征图中的两个自特征图相加得到的特征图的集合。

上图是一个二维卷积操作，这一操作也可以被扩展至$N$维，如果是三维卷积，那么卷积核将在长宽高三个轴上面滑动。
定义离散卷积核的集合有一个形状，它对应于一个函数的某种排列$(n,m,k_1,...,k_N)$,其中：
$n:输出特征图的数量$
$m:输入特征图的数量$
$k_j:卷积核在第j个维度上的尺寸$

下面的属性会影响卷积层在第$j$个轴上输出的大小：
$i_j：输入特征图在第j个轴上的尺寸$
$k_j:卷积核在第j个轴上的尺寸$
$s_j:沿第j个轴移动的步长$
$p_j:在第j个轴上进行0填充的大小（在轴的开头和结尾连接的零的数量）$
注意：跨步（stride）构成了一种子采样的形式，其可以作为卷积核转换了多少的度量，也可以被看做输出被保留了多少。
如下图，跨度为2的卷积等同于跨度为1的卷积只保留奇数输出元素。

池化（pooling）

池操作通过使用某些函数（例如取平均值或最大值）来汇总子区域，从而减小特征图的大小。
池化操作通过在输入特征图上移动滑窗并且将窗口内的内容诉讼给一个池化函数。从某种意义上讲，池化的工作方式非常类似于离散卷积，但它用其他函数代替了卷积核的线性组合描述。
下列参数影响了卷积层第$j$个轴输出特征图的尺寸$o_j$：
$i_j:输入特征图第j个轴上的尺寸$
$k_j:池化窗口在第j个轴上的大小$
$s_j:在第j个轴上移动的步长$
下图是平均池化的运算过程示意图，其中步长为1：

下图是最大池化的运算过程示意图，步长为1：

卷积算法

卷积层特性之间的关系的分析由于它们不跨轴相互作用而变得容易。例如，在$j$轴上选择的卷积核大小、步长和零填充大小只会影响输出特征图在j轴上的尺寸。
为了简化描述，做了如下假设：

1. 采用的是二维的卷积
2. 输入特征图为方形（$1_1=i_2=i$）
3. 卷积核为方形（$k_1=k_2=k$）
4. 卷积核沿每个轴移动的步长都相同（$s_1=s_2=s$）
5. 在每个轴上的零填充大小都相同（$p_1=p_2=p$）
   以上假设仅仅是为了简化分析和方便可视化，不过这些操作均可以被扩展至N维特征图。

无零填充，单位步长

这是最简单的情况，仅仅使用卷积核划过输入特征图的每个位置，下图展示了$i=4,k=3$时的例子：

卷积核从输入特征图的最左边开始移动，每次移动一个位点，直到它触及输入的右侧。输出的大小将等于移动的步数加一，加一是因为卷积核具有初始位置。同样可以将此逻辑应用在高轴上。
最终可以得到下列关系：
$$o=(i-k)+1\text{\hspace{1em}(1)}$$

其中$s=1,p=0$.

零填充，单位步长

考虑零填充的时候（仅限$s=1$），输入图像的尺寸从$i$变为$i+2p$。上述关系式可以写为：
$$o=(i-k)+2p+1\text{\hspace{1em}(2)}$$
下图展示了$i=5,k=4,p=2$时的一个例子：

半（half/same）填充

可以另输出特征图的尺寸和输入特征图相同。
对于任意的$i$和奇数$k(k=2n+1,n\in \mathbb{N}),s=1,p=[k/2]=n$,有如下关系：
$$\begin{gathered} o=i+2[k/2]-(k-1) \\ =i+2n-2n \\ =i\text{\hspace{1em}(3)} \end{gathered}$$
下图提供了一个$i=5,k=3,p=1$的示例：

全填充

进行卷积操作时，通常会使输出特征图的尺寸相对于输入有所减小，不过有时候，我们需要得到想反的结果。可以通过适当的零填充来实现这一目的。
对于任意的$i，k$,以及$p=k-1,s=1$，有如下关系：
$$\begin{gathered} o=i+2(k-1)-(k-1) \\ =i+(k-1)\text{\hspace{1em}(4)} \end{gathered}$$
下图展示了$i=5,k=3,s=1,p=2$时的例子：

无零填充，非单位步长

前面推导的关系式全部是在单位步长的情况下得到的。对于非单位步长则需要另外的推导方法。为了便于分析，暂时忽略零填充（$s>1,p=0$）如下图$i=5,k=3,s=2$：

同样，输出大小可以根据j卷积核在输入上放置的数量或者说出现的位置数量来定义。
考虑宽度轴：卷积核从输入的最左边开始移动，不过这次他移动的步长为s，直到它到达输入的右侧。输出的大小等于所移动的步数加上1，同样的逻辑也可以应用在高度轴上。
对于任意的$i,k,s$以及另$p=0$，有如下关系式：
$$o=[\frac{i-k}{s}]+1\text{\hspace{1em}(5)}$$

通过上面关系式，我们可以看出，这种卷积操作有可能存在卷积核的最后一次移动不被包含在内的情况（$\frac{i-k}{s}$有余数）。如下图，卷积核从左向右移动时，最后一次移动将会使卷积核超出特征图的边缘，所以这次移动被舍弃：

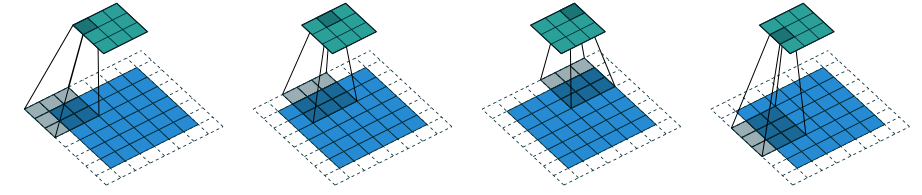
零填充，非单位步长

使用非单位步长和零填充才是最一般的情况。
对于任意的$i,k,p,s$，有
$$o=[\frac{i+2p-k}{s}]+1\text{\hspace{1em}(6)}$$
这一函数说明，卷积操作可能为多种不同的输入尺寸产生相同的输出尺寸。举例说明，如果$i+2p-k$是$s$的倍数，则任意输入尺寸$j=i+a,a\in 0,...,s-1$都会产生相同的输出尺寸。
下图是

下图是当$i=5,k=3,s=2,p=1$时的卷积操作

池化算法

池化层可以为输入的小平移提供不变性，Uzi常见的是最大池化，他将输入分割成一般互不重叠的小块，输出每个小块中的最大值。还有平均池化，他们的思路是一样的，都是对某些小块（patch）里的内容应用得先性来局部的将输入信息进行聚合。
卷积算法的处理依赖于假设某些函数被重复应用于输入的子集，这意味着上一层产生的关系可以在池化运算中被重用。
池化操作不涉及零填充，因此关系式如下：
对于任意的$i,k,s$
$$o=[\frac{i-k}{s}]+1\text{\hspace{1em}(7)}$$
这一关系式在任何池化操作中均有效。

逆卷积（Transpose convolution）

当需要与正常卷积方向相反的变换时，就用到了转置卷积。例如，从某个具有其卷积输出形状的特征图到具有其输入形状的特征图的转换，同时还要保留与所述卷积兼容的连接模式。转置卷积可以作为卷积自动编码器的解码层或者将特征图映射到一个更高维度的空间。
卷积操作要比全连接复杂的多，全连接只需要使用一个经过转置（这个表达有待商榷）的权重矩阵。不过每个卷积操作总结来说都是一个矩阵操作的有效运算，卷积操作与全连接有相似之处。
与卷积算法一样，逆卷积算法的研究也因其各个轴上的性质相互独立而得到简化。
做以下假设：
$$\begin{gathered} 1.采用二维逆卷积 \\ 2.输入为方形（i_1=i_2=i） \\ 3.卷积核尺寸为方形(k_1=k_2=k) \\ 4.在每个轴上移动的步长相同(s_1=s_2=s) \\ 5.在每个轴上零填充的大小一致(p_1=p_2=p) \end{gathered}$$
同样，所有的操作都可以扩展至N维。

用矩阵运算表示卷积

以下图为例：

如果将输入和输出从左到右，从上到下展开成向量，这个卷积操作可以表示成一个稀疏矩阵$C$,其中非零元素是卷积核中的元素${\omega }_{i,j}$其中$i,j$分别表示行和列。
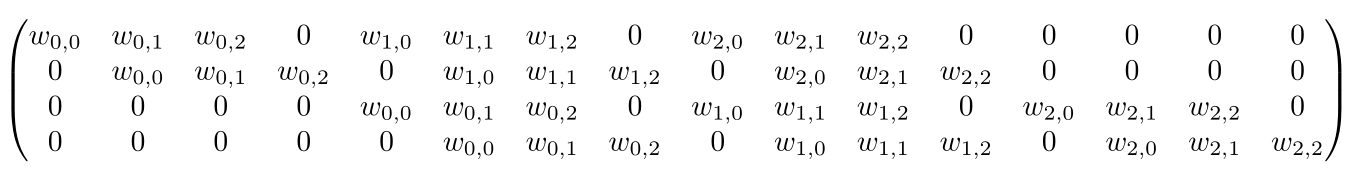（实在懒得敲了这个矩阵）
这个线性运算将输入矩阵展开成十六维的向量并且生成一个四维的向量，这个向量随后被重定型为$2\ast 2$的输出矩阵。
利用这种表示方法，通过对$C$转置很容易获得反向过程。换言之，就是通过将$loss$和$C^T$相乘得到误差进行反向传播。这一操作将四维的向量作为输入并且产生一个16维的向量作为输出，其连接模式和$C$的结构兼容。
卷积核$w$定义了用于前向传播和反向传播的$C$和$C^T$矩阵。

逆卷积

逆卷积也被称为跨步卷积（fractionally stride convolutions）或者反卷积（deconvolutions）通过交换卷积的前向和后向传递过程来工作。卷积核定义了一种卷积操作，但是他是直接卷积还是逆卷积还要取决于前向传播和反向传播的计算方式。
例如，虽然卷积核$w$定义了一个前行传播和反向传播是通过与$C$和$C^T$分别相乘的卷积操作，不过同时他也定义了一个前向传播和反向传播是通过与$C^T$和$(C^T{)}^T=C$分别相乘的卷积操作。
要注意，始终可以使用直接的卷积来模拟逆卷积。缺点是输入中的很多列和行都是0，这导致了实现效率大大降低。

无零填充，单位步长逆卷积

我们可以将逆卷积的输入图像想象为在某个初始特征图上进行直接卷积得到的结果。逆卷积可以看做是将特征图恢复成原始大小（进行直接卷积之前的大小）的操作，不过这里需要注意，仅仅是恢复尺寸，并不能保证恢复后的内容也完全一致。
假设一个$3\ast 3$卷积核在一个$4\ast 4$输入上面，采用单位步长，无填充，即：$i=4,k=3,s=1,p=0$如图：

上图是产生了一个$2\ast 2$的输出。逆卷积则是相反的过程，他是在一个$2\ast 2$的输入上应用逆卷积，输出一个$4\ast 4$的特征图。
另一种获得逆卷积结果的方法是使用等效的直接卷积，不过这种方法的效率要低很多。如下图，对$2\ast 2$的输入特征图进行一个$2\ast 2$的填充，然后使用$3\ast 3$的卷积核进行单位步长的卷积得到。这里卷积核和步长的大小都保持不变，不过输入特征图是经过零填充的。

理解零填充背后逻辑的一种方式是考虑到逆卷积的连通模式并且利用它来知道等效卷积的设计。例如，直接卷积输入特征图左上方的像素点值对输出特征图的左上方像素点起作用，输入右上方的像素点只连接输出右上方的像素点，依次类推。
为了在等效卷积中保持相同的连通模式，对输入进行零填充是有必要的，这样可以另第一个卷积（左上角）只接触到输入的第一个元素，即，填充尺寸应该等于卷积核的尺寸减一。
按照同样的方式进行，可以在图像的而其他元素观察到类似的结果，产生如下关系：
一个满足条件$s=1,p=0$尺寸为$k$的卷积有一个与之联系的转世卷积，这个逆卷积的尺寸与卷积一样$(k^{\prime }=k)$，步长一样$(s^{\prime }=s)$,填充尺寸为$p^{\prime }=k-1$，那么这个逆卷积的输出特征图尺寸为：
$$o^{\prime }=i^{\prime }+(k-1)\text{\hspace{1em}(8)}$$

零填充，单位步长逆卷积

我们已经知道，无填充卷积的逆卷积等价于对一个经过零填充的输入特征图进行直接卷积，我们可以假设一个零填充卷积的逆卷积等价于对一个经过较小尺寸的零填充的输入特征图进行直接卷积。
如下图，用$4\ast 4$卷积核对一个经过$2\ast 2$零填充的$5\ast 5$输入特征图进行步长为1的卷积（$i=5,k=4,s=1,p=2$）的逆卷积等价于用一个$4\ast 4$的卷积核对一个经过$1\ast 1$填充的$6\ast 6$的特征图进行步长为1的卷积操作。

可以总结出如下关系：
对于一个用$s=1,k,p$描述的卷积，与他相联系的逆卷积可以被描述为：$k^{\prime }=k,s^{\prime }=s,p^{\prime }=k-p-1$，输出特征图的尺寸为：
$$o^{\prime }=i^{\prime }+(k-1)-2p\text{\hspace{1em}(9)}$$

半填充（Half（same） padding）逆卷积

利用前面归纳推理的方法，可以预测，板田冲之后的卷积操作的逆卷积的等效卷积本身也是一个半填充卷积，其数出尺寸与输入尺寸大小相同。因此可以得到以下关系：
与一个通过$k=2n+1,n\in \mathbb{N},s=1,p=[\frac{k}{2}]=n$描述的卷积相关联的逆卷积可以被描述为：$k^{\prime }=k,s^{\prime }=s,p^{\prime }=p$其输出尺寸为：
$$\begin{gathered} o^{\prime }=i^{\prime }+(k-1)-2p \\ =i^{\prime }+2n-2n \\ =i^{\prime }\text{\hspace{1em}(10)} \end{gathered}$$
如下图，一个使用$3\ast 3$卷积核对一个经过半填充的$5\ast 5$输入特征图进行单位步长的卷积操作的逆卷积等效于使用一个$3\ast 3$的卷积核对一个经过半填充的$5\ast 5$特征图进行单位步长的卷积操作。

全填充，逆卷积

我们已经知道无填充卷积的逆卷积的等效卷积中包含了全填充，因此我们可以得到，全填充卷积的逆卷积的等效卷积是无填充卷积。
如下图，使用一个$3\ast 3$卷积核对一个经过全填充的$5\ast 5$输入特征图进行单位步长的卷积的逆卷积等价于使用一个$3\ast 3$的卷积核对一个无填充的$7\ast 7$输入特征图进行卷积。

可以得到如下关系：
一个由$s=1,k,p=k-1$描述的卷积对应的逆卷积可描述为：$k^{\prime }=k,s^{\prime }=s,p^{\prime }=0$其输出尺寸为：
$$\begin{gathered} o^{\prime }=i^{\prime }+(k-1)-2p \\ =i^{\prime }-(k-1)\text{\hspace{1em}(11)} \end{gathered}$$

非零填充，非单位步长逆卷积

使用与零填充相同的归纳逻辑，可以预测一个$s>1$的卷积的逆卷积包含一个$s<1$的等效卷积。
下图是一个$3\ast 3$卷积在一个$5\ast 5$的特征图上进行步长为2的卷积的逆卷积等效于用一个$3\ast 3$的卷积对一个经过$2\ast 2$填充的$2\ast 2$(在输入的每个相邻像素之间插入了1个0)特征图。因为在输入图像的元素之间插入了0，所以容易理解，这种情况下卷积的移动速度可以看做比1小。

假设卷积是无填充的（$p=0$），其输入尺寸$i-k$是$s$的倍数，可以得到下列关系：
一个由$p=0,k,s$描述的卷积，并且其输入尺寸$(i-k)$是$s$的倍数，与之对应的逆卷积可以被描述为：$\widetilde{i^{\prime }},k^{\prime },s^{\prime }=1,p^{\prime }=k-1$其中$\widetilde{i^{\prime }}$是通过在输入特征图的每个单元之间添加$s-1$个0之后得到的拉伸后的输入，最终输出尺寸为：
$$o^{\prime }=s(i^{\prime }-1)+k\text{\hspace{1em}(12)}$$

零填充，非单位步长逆卷积

当输入尺寸为$i+2p-k$是$s$的倍数时，根据先前的关系式可以推导出：
有个由$k,s,p$描述的卷积核且其输入图像尺寸为$i+2p-k$是$s$的倍数，那么与他对应的逆卷积可由$\widetilde{i^{\prime }},k^{\prime }=k,s^{\prime }=1,p^{\prime }=k-p-1$,其中$\widetilde{i^{\prime }}$是拉伸后的输入，输出尺寸为：
$$o^{\prime }=s(i^{\prime }-1)+k-2p\text{\hspace{1em}(13)}$$
如下图，一个$3\ast 3$卷积核在一个经过$1\ast 1$填充的$5\ast 5$输入上以步长为2进行卷积的逆卷积等效为用一个$3\ast 3$卷积核在一个经过$1\ast 1$填充的$3\ast 3$输入（在像素之间插入一个0像素之后）上进行步长为1的卷积操作。

可以通过引入另一个参数 a ∈ { 0 , . . . , s − 1 } a\isin\{0,...,s-1\} a∈{0,...,s−1}来放松对输入尺寸的限制，这样便可以区分导致相同的$i^{\prime }$的不同$s$的情况。
与由$k,s,p$描述的卷积操作对应的逆卷积操作可以由$a,\widetilde{i^{\prime }},k^{\prime }=k,s^{\prime }=1,p^{\prime }=k-p-1$描述，其中$\widetilde{i^{\prime }}$是经过拉伸之后的输入特征图的尺寸，$a=(i+2p-k)$，$s$代表添加到输入特征图底部和右侧的零的个数，输出尺寸为：
$$o^{\prime }=s(i^{\prime }-1)+a+k-2p\text{\hspace{1em}(14)}$$
如下图，用$3\ast 3$卷积核在一个经过$1\ast 1$填充的$6\ast 6$输入特征图上进行步长为2的卷积操作的逆卷积等效为用一个$3\ast 3$卷积核在一个经过$1\ast 1$填充并且在底部和右侧额外增加了一行（列）0填充的$3\ast 3$输入特征图上进行步长为1的卷积操作。

其他卷积

膨胀卷积（dilated convolutions/strous convoutions）

膨胀卷积通过在卷积核的元素之间插入空格（空元素）来达到扩张卷积核的效果，扩张率有一个附加的超参数$d$控制。通常会在卷积核的各元素之间插入$d-1$个空格，当$d=1$时，卷积核就变为普通卷积核。
扩张卷积用来在不增加内核大小的情况下增大输出的感受野，当使用多个膨胀卷积叠加相乘时效果更加明显。
为了弄清楚膨胀率和输出尺寸之间的关系，需要考虑膨胀率$d$对有效卷积核尺寸的影响。一个尺寸为$k$的卷积核经过膨胀率为$d$的膨胀之后，有效尺寸变为：
$$\hat{k}=k+(k-1)(d-1)$$
这个关系是和式（6）结合可以得到下列关系：
对于任意$i,k,p,s$在膨胀率为$d$时，
$$o=[\frac{i+2p-k-(k-1)(d-1)}{s}]+1\text{\hspace{1em}(15)}$$
如下图，使用一个膨胀率为2的$3\ast 3$卷积核对一个$7\ast 7$的输入特征图进行卷积操作。参数设置为：$(i=7,k=3,d=2,s=1,p=0)$

以上为个人对阅读论文的一个小总结，也可以看做是一个翻译吧，其中有表达不准确的地方，或者右不同的看法见解的欢迎评论或者私信我哦，希望大家一起进步。