Chen系统的有限时间驱动-响应同步

混沌的发展简史

混沌理论的基本思想起源于20世纪初, 形成于20世纪60年代, 20世纪60-70年代是混沌研究发展突飞猛进的时代, 发展壮大于20世纪80年代.
1903年, 美国数学家Poincare J.H.在《科学与方法》中提出了Poincare猜想, 结合拓扑系统与动力学系统两大领域, 指出了混沌存在的可能性. 1963年, E.N.Lorenz教授提出Lorenz系统而被誉为“混沌学之父”, 开辟了混沌发展的新纪元.
1970年, 美国科学史家Kuhn T.S.发表的《科学革命的结构》一书, 推动了混沌理论的发展.1975年, 中国学者李天岩和他的导师美国数学家Yorke J.发表的《周期3蕴含混沌》一文, 首次提出了“混沌”一词, 为这一新兴研究领域确立了一个中心概念. 自此, “混沌（Chaos）”一词被正式使用. 该论文在当时震动整个学术界, 深刻揭示了从有序到混沌的演化过程. 随后, 美国生物学家May于1976年在《自然》上发表的名为《具有复杂动力学特性的简单数学模型》一文, 以一维平方映射为研究对象, 并指出在这类简单的一维映射中也存在着信周期分叉以及混沌现象, 促使不同领域的混沌学研究联成一体. 1977年, 在意大利召开的第一次国际混沌会议, 标志着混沌学的诞生.
1978年, 美国物理学家Feigenbaum M.J.在《统计物理杂志》上发表了文章《一类线性变换的定量普适性》, 针对该类一维映射, 利用重整化群思想, 提出了倍周期分叉通向混沌的两个普适常数. 正是他的普适性的研究为混沌行为奠定了基础, 具有里程碑意义. 1980年, 法国数学家Mandelbrot绘出世界上第一张Mandelbrot集的混沌图像. 1984年, 我国科学家郝柏林出版的《混沌》一书, 在一定程度上推动了混沌科学的发展. 1986年, 我国第一届混沌会议在桂林召开, 中国科学家徐京华第一个在世界上提出三种神经细胞的复合网络, 并证明它存在混沌. 指出人脑可看成是复杂的多层次混沌动力学系统, 脑功能的物理基础是混沌性质的过程.
目前, 混沌已被广泛应用于数学、物理、化学、心理学、医学、气象学、经济学以及信息科学等许多领域. 混沌也是第一个将众多的学科和领域紧紧联系在一起的概念.

混沌的基本性质

混沌现象是非线性系统的普遍属性, 它蕴含着丰富的信息和复杂多样的形状, 这些互不相同的混沌现象却具有某些共同的属性.
（1）敏感性
敏感性是混沌最本质的属性.一方面反映的是：在非线性动力学系统内, 随机性系统运动趋势的强烈影响. 即混沌系统中复杂的拉伸、折叠等非线性变换放大了初始条件的微小变化, 掩盖了初始条件所包含的系统全部信息, 使得初始条件的微小变化都会使得系统的运动轨迹出现极大的分离；另一方面也导致了系统将会出现长期时间行为的不可预测性, 但由于混沌系统是一个确定性系统, 所以, 它在短期内还是可以预测的.
（2）内随机性
混沌具有内随机性, 系统处于混沌状态是由于系统内部动力学随机性而产生的不规则行为, 常称之为内随机性, 混沌系统产生的类似随机的行为, 只能是由系统内部产生的, 而非外界随机因素的影响. 尽管混沌系统表现出类似随机的行为, 但却又不是随机系统, 所以, 混沌介于确定与随机之间, 是有序和无序的统一.
（3）具有正的Lyapunov指数
系统的Lyapunov指数是系统相空间中相近轨道的平均收敛性或发散性的一种度量, 从本质上刻画了混沌运动中的局部不稳定性, 即混沌系统的相邻轨线不断排斥, 最终会以指数速度相互分离. 不管系统是一般混沌系统还是超混沌系统, 它都是具有正的Lyapunov指数.
总之, 混沌的基本性质在不同文献的表述不尽相同. 简单而论, 如果一个系统具有以上三个性质, 则称之为混沌系统.

同步的基本方法

本节仅对混沌同步的驱动—响应法作简要的介绍.
19世纪末, 美国学者L.M.Pecora和T.L.Carrll首先提出驱动-响应同步法, 简称P-C同步法[17]. 其基本思想是：把驱动系统分解成稳定的和不稳定的两个子系统, 对不稳定的子系统复制一个响应系统, 来实现这两个系统的同步.
驱动-响应同步法的动力系统模型为：


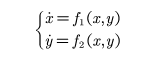
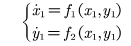
令

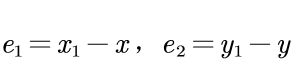
则可以得到同步的误差子系统

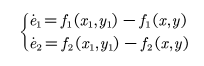
构造误差系统的Lyapunov指数, 再根据Lyapunov稳定性原理来判别系统的同步稳定性. 只有当响应系统的所有条件Lyapunov指数都是负值时, 才能达到响应系统和驱动系统的同步.
该方法的主要特点是:两个非线性动力学系统之间存在着驱动与响应关系. 响应系统行为取决于驱动系统, 而驱动系统的行为与响应系统的行为无关. 对于某些实际的非线性系统, 由于物理本质或天然特性等原因, 系统无法分解, 这时, P-C同步法也就无能为力了. 因此, 驱动-响应同步法具有一定的局限性

应用实例

考虑一类chen系统表示如下：
$$\{\begin{array}{l}\dot{x}=a\left(y-x\right)\\ \dot{y}=\left(c-a\right)x-xz+cy\\ \dot{z}=xy-bz\end{array}$$
在MATLAB中表示如下

dy(1)=a*(y(2)-y(1));
dy(2)=(c-a)*y(1)-y(1)*y(3)+c*y(2);
dy(3)=y(1)*y(2)-b*y(3);

构造如下非线性控制器：
$$u=\left(\begin{array}{c}0\\ \left(u-c\right)y+xz\\ -xy\end{array}\right)$$
在MATLAB中表示如下：

function out =funD(x,y,z)
c=28;u=5;
out=[0;(u-c)*y+x*z;-x*y];

利用驱动和响应系统得到相应的误差同步动态系统，证明误差同步动态系统在有限时间内收敛于零，则可以得到chen系统作为驱动系统与响应系统在有限时间内达到同步，同步系统与驱动系统程序如下：

function dy=chen(~, y)
format long
a=35;b=3;c=28;
% dy=zeros(3, 1);
% dy(1)=a*(y(2)-y(1));
% dy(2)=(c-a)*y(1)-y(1)*y(3)+c*y(2);
% dy(3)=y(1)*y(2)-b*y(3);
%同步
global m n;
u=5;
dy=zeros(6, 1);
D1=funD(y(1),y(2),y(3));
D2=funD(y(4),y(5),y(6));
%驱动系统
dy(1)=a*(y(2)-y(1))+m*0;
dy(2)=(c-a)*y(1)-y(1)*y(3)+c*y(2) +m*(D1(2,:)-D2(2,:));
dy(3)=y(1)*y(2)-b*y(3)+m*(D1(3,:)-D2(3,:));
%响应系统
dy(4)=a*(y(5)-y(4))+n*0;
dy(5)=(c-a)*y(4)-y(4)*y(6)+c*y(5)+n*(D2(2,:)-D1(2,:));
dy(6)=y(4)*y(5)-b*y(6) +n*(D2(3,:)-D1(3,:));

再进而根据主函数程序可以得到误差动态系统在有限时间同步的仿真图像：

function chen_main
%耦合系数对同步的影响
clear;clc;
global m n;
format long;
tspan = 0:0.001:5;
Y0 = [3 4 20 4 5 21];
hold on 
m=2.05;n=0.5;
[t,y]=ode45(@chen,tspan,Y0);
plot(t, y(:,4)-y(:,1),'r',t,y(:,5)-y(:,2),t,y(:,6)-y(:,3))
legend('m2.05,n=0.5')

运行程序后可得仿真图为：

由此可知，该系统可在有限时间内达到稳定状态。