最近想复习一下数学知识,才看到偏导数就感到“温故而知新“了。以前学高数的时候经常求偏导数,到最后就光记住怎么算了,这里带着实际意义总结一下。
偏导数的的定义就不写了,看了一下百度百科的定义是这样写的:

感觉实在是没有什么意义……
从简单(普通导数)开始。我们都知道,对于一元函数而言,比如y=ax+b, 显然对x求导可以得到函数的变化率。

在上图这个函数中,只存在y随x的变化情况。对x求出的导数也就是y在x上的变化率。
然而对于二元函数,比如z=f(x,y),我们知道z不仅随x变化,还随y变化,因此情况就复杂了很多。

如上图,我们把二元函数想象成一个面。偏导数几何含义是这样的:
求对x的偏导数:对于x求导,(在y值固定的情况下)就得到了平面上某一条曲线(比如图中平面上中间竖着的虚线)在x方向上的变化率,也就是对x轴的斜率。
求对y的偏导数:对于y求导,(在x固定的情况下)就得到了平面上某一条曲线(比如图中平面上中间横着的虚线)在y方向上的变化率,也就是对y轴的斜率。
总而言之,对哪个值求偏导,就会得到函数在哪个轴上的变化率。若我们仅仅对x“求导“,得到的其实就是x的偏导数,它的含义是z在x方向上的变化率。
偏导数的表达方式有很多种,以下几种都是对x求偏导数的写法:
![]()
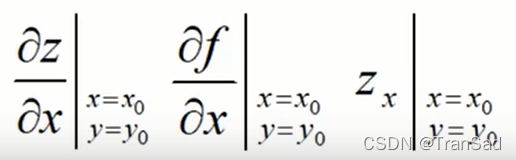
在一些机器学习公式推导或者是神经网络梯度下降的过程当中可能会遇到这些表达方式,熟悉一下,以后知道是偏导数即可。








 本文介绍了偏导数的概念,通过一元函数和二元函数的对比,阐述了偏导数在几何上的含义。偏导数是对二元函数在特定变量上的变化率,表示函数在某一轴上的变化趋势。在机器学习和神经网络中,偏导数是求解梯度和优化算法的关键。
本文介绍了偏导数的概念,通过一元函数和二元函数的对比,阐述了偏导数在几何上的含义。偏导数是对二元函数在特定变量上的变化率,表示函数在某一轴上的变化趋势。在机器学习和神经网络中,偏导数是求解梯度和优化算法的关键。

















 2666
2666

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










