5.4 胶片与成像 - Physically Based Rendering From Theory To Implementation(PBRT)

最新推荐文章于 2024-03-23 19:49:13 发布
最新推荐文章于 2024-03-23 19:49:13 发布
阅读量260 收藏
点赞数
分类专栏： 离线渲染 文章标签： 数码相机 图形渲染 离线渲染 PBRT
原文链接：https://pbr-book.org/4ed/Cameras_and_Film/Film_and_Imaging
版权

Physically Based Rendering From Theory To Implementation

翻译：https://pbr-book.org/4ed/Cameras_and_Film/Film_and_Imaging

总目录： Physically Based Rendering From Theory To Implementation - 基于物理的渲染从理论到实践第四版原书翻译

文章目录

5.4 Film and Imaging 胶片与成像

当相机的投影或镜头系统在胶片上形成场景的图像后，有必要对胶片如何测量光线来创建由渲染器生成的最终图像进行建模。本节首先概述如何在胶片上测量光的辐射学，然后继续讨论光谱能量如何转换为三刺激颜色(通常为RGB)。这就产生了PixelSensor类，它对该过程以及通常由相机执行的进一步处理进行建模。在考虑了胶片上的图像样本如何累积为最终图像的像素之后，我们介绍了Film接口以及两种将该模型付诸实践的实现。

5.4.1 The Camera Measurement Equation 摄像机测量方程

给定真实成像过程的模拟，更仔细地定义由胶片或相机传感器测量的辐射度也是值得的。从透镜后方到胶片的光线携带着来自场景的辐射度。因此，从胶片平面上的一点考虑，有一组辐射入射的方向。离开透镜的辐射度分布受到胶片上的点所看到的散焦模糊量的影响——图5.17显示了从胶片上的两个点所看到的来自透镜的辐射度的两幅图像。
在这里插入图片描述在这里插入图片描述
图5 - 17： 从胶片平面上的两个点看到的场景在镜头上的图像这两幅画都来自圣米格尔的场景。(a)从景物处于清晰焦点的点上看;入射辐射在其面积上实际上是恒定的。(b)从离焦区域的像素处看，可以看到部分场景的小图像，其亮度可能快速变化。

给定入射辐射度函数，我们可以定义薄膜平面上一点的辐照度。如果我们从用(4.7)式的辐射度定义辐照度开始，那么我们可以用(4.9)式将对立体角的积分转换为对面积的积分(在本例中， A e A_e Ae​是与后透镜元素相切的平面面积)。这将给出film平面上某个点p的辐照度:

E ( p ) = ∫ A e L i ( p , p ′ ) ∣ c o s θ c o s θ ′ ∣ ∥ p ′ − p ∥ 2 d A e E(p) = \int_{A_e} L_i(p,p') \frac{|cos\theta cos\theta'|}{\|p'-p \|^2} dA_e E(p)=∫Ae​​Li​(p,p′)∥p′−p∥2∣cosθcosθ′∣​dAe​

图5.18显示了情况的几何形状。
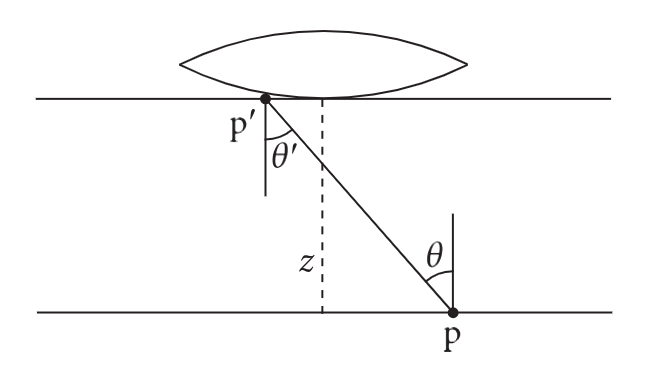
在这里插入图片描述
图5.18: 辐照度测量方程(5.3)的几何设置。当它通过与后透镜元件相切的平面上的点 p ′ p' p′到胶片平面上的点 p p p时，可以测量亮度。 z z z为胶片平面到后元件切平面的轴向距离， θ \theta θ为从 p ′ p' p′至 p p p的矢量与光轴之间的夹角。

因为胶片平面平行于透镜平面， θ = θ ′ \theta = \theta' θ=θ′。我们可以进一步利用 p p p和 p ′ p' p′之间的距离等于从胶片平面到透镜的轴向距离(我们将在这里表示为z)除以 c o s θ cos\theta cosθ的事实。综上所述，我们有

E ( p ) = 1 z 2 ∫ A e L i ( p , p ′ ) ∣ c o s 4 θ ∣ d A e E(p) = \frac{1}{z^2} \int_{A_e} L_i(p,p') |cos^4\theta| dA_e E(p)=z21​∫Ae​​Li​(p,p′)∣cos4θ∣dAe​

对于胶片的范围相对于距离z来说比较大的相机，这个 c o s 4 θ cos^4\theta cos4θ项可以有意地减少入射辐照度——这个因素也有助于渐晕。大多数现代数码相机都使用预设的校正因子来校正这种效果，这些校正因子会增加传感器边缘的像素值。

在快门打开的时间内，将胶片上某一点的辐照度积分得到辐射曝光【radiant exposure】，这是每单位面积能量的辐射单位， J / m 2 J/m^2 J/m2

H ( p ) = 1 z 2 ∫ t 0 t 1 ∫ A e L i ( p , p ′ , t ′ ) ∣ c o s 4 θ ∣ d A e d t ′ H(p) = \frac{1}{z^2} \int_{t_0}^{t_1} \int_{A_e} L_i(p,p',t') |cos^4\theta| dA_e dt' H(p)=z21​∫t0​t1​​∫Ae​​Li​(p,p′,t′)∣cos4θ∣dAe​dt′

(辐射暴露也被称为fluence。)测量某一点的辐射曝光，可以得到底片上接收到的能量与相机快门打开的时间长短有部分关系。

照相胶片(或数码相机中的CCD或CMOS传感器)测量小范围内的辐射能。取式(5.4)，对传感器像素面积 A p A_p Ap​积分，得到

J = 1 z 2 ∫ A p ∫ t 0 t 1 ∫ A e L i ( p , p ′ , t ′ ) ∣ c o s 4 θ ∣ d A e d t ′ d A p J = \frac{1}{z^2} \int_{A_p} \int_{t_0}^{t_1} \int_{A_e} L_i(p,p',t') |cos^4\theta| dA_e dt' dA_p J=z21​∫Ap​​∫t0​t1​​∫Ae​​Li​(p,p′,t′)∣cos4θ∣dAe​dt′dAp​

焦耳到达一个像素;这被称为相机测量方程。

虽然这些因素适用于本章介绍的所有相机模型，但它们只包含在RealisticCamera的实现中。原因纯粹是实用主义:大多数渲染器不会对这种效果进行建模，因此从更简单的相机模型中省略它，可以更容易地比较pbrt渲染的图像与其他系统渲染的图像。

5.4.2 Modeling Sensor Response 传感器响应建模

传统的胶片是基于一种化学过程，卤化银晶体暴露在光线下会产生溴化银。卤化银对蓝光最敏感，但彩色图像可以通过多层晶体和使卤化银对其他波长更敏感的染料获得。

现代数码相机使用CCD或CMOS传感器，每个像素通过将光子转化为电荷有效地计算它暴露在光子中的数量。人们已经开发了各种各样的彩色图像捕捉方法，但其中最常见的是在每个像素上安装一个彩色滤光片，以便通过只计算通过滤光片的光子来测量红、绿或蓝。每个像素通常都补充了一个微透镜，以增加到达传感器的光量。

对于胶片和数字传感器，像素的颜色测量可以用光谱响应曲线来建模，该曲线描述了滤色片或胶片对光的化学响应作为波长的函数。这些函数的定义如下，例如，给定一个入射光谱分布 S ( λ ) S(\lambda) S(λ)，像素的红色分量为

r = ∫ s ( λ ) r ˉ ( λ ) d λ r = \int s(\lambda) \bar{r}(\lambda) d\lambda r=∫s(λ)rˉ(λ)dλ

由于人类视觉系统对绿色更敏感，数字传感器像素通常以马赛克【**mosaics **】形式排列，绿色像素是红色和蓝色像素的两倍。像素马赛克的一个含义是，必须使用去马赛克算法【demosaicing algorithm】将这些传感器像素转换为红色、绿色和蓝色组件所在的图像像素。由于组成传感器的像素在位置上略有不同，因此将拼接像素作为四分块并直接使用其颜色值的简单方法效果不佳。

设计数字传感器面临许多挑战，其中大部分来自于像素尺寸太小，这是高分辨率图像需求的结果。一个像素越小，在给定的镜头和曝光时间下，它暴露在的光子就越少，反过来，就越难准确测量光。像素阵列受到各种类型噪声的影响，其中散点噪声通常是最显著的。这是由于光子的离散性质:在被计数的光子数量中存在随机波动，捕获的光子数量越少，这一点就越重要。散粒噪声可以用泊松分布来建模。

每个像素必须接收到足够的光，要么引起必要的化学反应，要么计算出足够的光子来捕捉准确的图像。由式(5.5)可知，在一个像素处捕获的能量取决于入射辐射、像素面积、出瞳面积和曝光时间。对于给定的相机设计，像素面积是固定的，增加镜头光圈面积和增加曝光时间都可能会引入不必要的副作用，以换取额外提供的光线。较大的光圈会降低景深，这可能会导致不期望的散焦模糊。长时间的曝光也会导致模糊，因为场景中有移动的物体，或者由于快门打开时相机运动。传感器和胶片因此提供了额外的控制形式的ISO设置。

对于物理胶片，ISO编码其对光的响应性(更高的ISO值需要更少的光来记录图像)。在数码相机中，ISO控制增益，即从传感器读取像素值时应用的缩放因子。对于物理相机，增益的增加会加剧噪声，因为初始像素测量中的噪声被放大。由于pbrt不模拟物理传感器读数中存在的噪声，因此可以任意设置ISO值以实现所需的曝光。

在pbrt的传感器模型中，我们既没有模拟马赛克，也没有模拟噪声，也没有模拟其他效果，比如泛光，即暴露在足够光线下的像素会“溢出”，并开始增加相邻像素的测量值。我们也没有模拟从传感器读取图像的过程:许多相机使用滚动快门，其中扫描线是连续读取的。对于物体快速移动的场景，这可以给出令人惊讶的结果。本章末尾的练习建议以各种方式修改pbrt，以探索这些效果。

PixelSensor类实现了pbrt的半理想像素颜色测量模型。它定义在文件film.h和film.cpp中。

<<PixelSensor Definition>>= 
class PixelSensor {
public:
    <<PixelSensor Public Methods>> 
    <<PixelSensor Public Members>> 
private:
    <<PixelSensor Private Methods>> 
    <<PixelSensor Private Members>> 
};

PixelSensor对传感器像素运行的三个部分进行建模:

  1. 曝光控制（Exposure controls）：这些是用户可设置的参数，用于控制图像的亮度或暗度。
  2. RGB响应（RGB response）：PixelSensor使用基于物理相机传感器测量的光谱响应曲线来模拟光谱辐射到三刺激颜色的转换。
  3. 白平衡（White balance）：相机通常会对捕获的图像进行处理，包括根据光照的颜色调整初始RGB值，以模拟人类视觉系统中的色彩适应。因此，捕捉到的图像在视觉上与人类观察者在拍照时所看到的相似。

PBRT包括现实摄像机模型和基于投影矩阵的理想化模型。由于针孔相机的孔径具有无穷小的面积，因此我们在实现PixelSensor时做了一些实用的权衡，以便用针孔模型渲染的图像不会完全黑。我们把它作为相机的责任来模拟光圈大小的影响。理想化的模型根本不考虑它，而RealisticCamera在<<Compute weighting for RealisticCamera ray>>片段中这样做。PixelSensor只计算快门时间和ISO设置。这两个因素被收集成一个单独的量，称为成像比。

PixelSensor构造函数将传感器的RGB匹配函数 r ˉ , g ˉ , b ˉ \bar{r},\bar{g},\bar{b} rˉ,gˉ​,bˉ、和成像比作为参数。它还需要用户请求的颜色空间作为最终输出的RGB值，以及指定场景中什么颜色被认为是白色的光源的光谱;这些将使光谱能量转换为传感器测量的RGB，然后在输出颜色空间中转换为RGB成为可能。

图5.19显示了相机响应建模的效果，将使用XYZ匹配函数来计算初始像素颜色的渲染与实际相机传感器的匹配函数进行比较。
在这里插入图片描述
在这里插入图片描述
图5.19精确建模相机传感器响应的效果。(a)使用像素传感器的XYZ匹配函数渲染的场景。(b)使用Canon EOS 5D相机测量的传感器响应曲线绘制的场景。注意，它们的色调略冷——橙色较少，蓝色较多。(场景由Beeple提供。)

<<PixelSensor Public Methods>>= 
PixelSensor(Spectrum r, Spectrum g, Spectrum b,
       const RGBColorSpace *outputColorSpace, Spectrum sensorIllum,
       Float imagingRatio, Allocator alloc)
    : r_bar(r, alloc), g_bar(g, alloc), b_bar(b, alloc),
      imagingRatio(imagingRatio) {
    <<Compute XYZ from camera RGB matrix>> 
}
<<PixelSensor Private Members>>= 
DenselySampledSpectrum r_bar, g_bar, b_bar;
Float imagingRatio;

传感器像素记录光线的RGB颜色空间通常与用户为最终图像指定的RGB颜色空间不同。前者通常是特定于相机的，由其像素色彩滤波器的物理特性决定，后者通常是设备无关的色彩空间，如sRGB或4.6.3节中描述的其他色彩空间之一。因此，PixelSensor构造函数计算一个从RGB空间转换为XYZ的3x3矩阵。从那里，它很容易转换到特定的输出颜色空间。

该矩阵是通过求解一个优化问题得到的。它从20多个光谱分布开始，代表来自标准化颜色图表的各种颜色块【patches】的反射率。构造函数在相机的颜色空间中计算这些块在相机的光源下的RGB颜色，以及它们在输出颜色空间的光源下的XYZ颜色。如果这些颜色分别由3x3列向量M表示，那么我们可以考虑以下问题:
M [ r 1 r 2 r n g 1 g 2 ⋯ g n b 1 b 2 b n ] ≈ [ x 1 x 2 x n y 1 y 2 ⋯ y n z 1 z 2 z n ] \mathbf{M}\left[\begin{array}{llll} r_{1} & r_{2} & & r_{n} \\ g_{1} & g_{2} & \cdots & g_{n} \\ b_{1} & b_{2} & & b_{n} \end{array}\right] \approx\left[\begin{array}{llll} x_{1} & x_{2} & & x_{n} \\ y_{1} & y_{2} & \cdots & y_{n} \\ z_{1} & z_{2} & & z_{n} \end{array}\right] M ​r1​g1​b1​​r2​g2​b2​​⋯​rn​gn​bn​​ ​≈ ​x1​y1​z1​​x2​y2​z2​​⋯​xn​yn​zn​​ ​
只要有三个以上的反射率，这是一个可以用线性最小二乘来解决的过度约束问题。

PixelSensor(Spectrum r, Spectrum g, Spectrum b,
       const RGBColorSpace *outputColorSpace, Spectrum sensorIllum,
       Float imagingRatio, Allocator alloc)
    : r_bar(r, alloc), g_bar(g, alloc), b_bar(b, alloc),
      imagingRatio(imagingRatio) {

	// Compute XYZ from camera RGB matrix
    <<Compute rgbCamera values for training swatches>>  
	<<Compute xyzOutput values for training swatches>> 
	<<Initialize XYZFromSensorRGB using linear least squares>> 	
}

给定传感器的光源，计算每个反射率的RGB系数的工作由ProjectReflectance()方法处理。

<<Compute rgbCamera values for training swatches>>= 
Float rgbCamera[nSwatchReflectances][3];
for (int i = 0; i < nSwatchReflectances; ++i) {
    RGB rgb = ProjectReflectance<RGB>(swatchReflectances[i], sensorIllum,
                                      &r_bar, &g_bar, &b_bar);
    for (int c = 0; c < 3; ++c)
        rgbCamera[i][c] = rgb[c];
}

为了获得良好的结果，用于此优化问题的光谱应该呈现各种具有代表性的真实光谱。在pbrt中使用的是基于标准色表的测量。

<<PixelSensor Private Members>>+= 
static constexpr int nSwatchReflectances = 24;
static Spectrum swatchReflectances[nSwatchReflectances];

ProjectReflectance()实用方法采用反射率和光源的光谱分布，以及三基色刺激色彩空间的三个光谱匹配函数 b ˉ i \bar{b}_i bˉi​。它返回颜色系数的三元组 c i c_i ci​，由
c i = ∫ r ( λ ) L ( λ ) b ˉ i ( λ ) d λ c_i = \int r(\lambda) L(\lambda) \bar{b}_i(\lambda) d\lambda ci​=∫r(λ)L(λ)bˉi​(λ)dλ

式 r r r中为光谱反射率函数， L L L为光源的光谱分布， b ˉ i \bar{b}_i bˉi​为光谱匹配函数。假设第二个匹配函数 b ˉ 2 \bar{b}_2 bˉ2​ 一般对应于亮度或至少某种绿色，即人类视觉系统最能引起最大反应的颜色，则返回的颜色三元组归一化为 ∫ L ( λ ) b ˉ 2 ( λ ) d λ \int L(\lambda)\bar{b}_2(\lambda)d\lambda ∫L(λ)bˉ2​(λ)dλ。这样，线性最小二乘拟合至少会根据视觉重要性粗略地对每个RGB/XYZ对进行加权。

ProjectReflectance()函数将颜色空间三元组类型作为模板参数，因此可以返回适当的RGB和XYZ值。它的实现遵循与Spectrum::InnerProduct()相同的一般形式，计算1 nm波长上的黎曼和，因此这里不包括它。

<<PixelSensor Private Methods>>= 
template <typename Triplet>
static Triplet ProjectReflectance(Spectrum r, Spectrum illum,
                                  Spectrum b1, Spectrum b2, Spectrum b3);

在输出颜色空间中计算XYZ系数的片段，<<Compute xyzOutput values for training swatches>>，通常与RGB的片段相似，不同的是它使用了输出光源和XYZ光谱匹配函数并初始化xyzOutput数组。因此，它也不包括在这里。

给定两个颜色系数矩阵，调用LinearLeastSquares()函数可以解决式(5.7)的优化问题。

// <<Initialize XYZFromSensorRGB using linear least squares>>= 
pstd::optional<SquareMatrix<3>> m =
    LinearLeastSquares(rgbCamera, xyzOutput, nSwatchReflectances);
if (!m) ErrorExit("Sensor XYZ from RGB matrix could not be solved.");
XYZFromSensorRGB = *m;

因为RGB和XYZ颜色是使用颜色空间各自的光源计算的，所以矩阵M也执行白色平衡。

<<PixelSensor Public Members>>= 
SquareMatrix<3> XYZFromSensorRGB;

第二个PixelSensor构造函数使用XYZ匹配函数来表示像素传感器的光谱响应曲线。如果在场景描述文件中没有指定特定的相机传感器，这是默认值。请注意，在这种用法中，成员变量r_bar、g_bar和b_bar的名称是错误的，因为它们实际上是X、Y和Z。

<<PixelSensor Public Methods>>+=  
PixelSensor(const RGBColorSpace *outputColorSpace, Spectrum sensorIllum,
       Float imagingRatio, Allocator alloc)
    : r_bar(&Spectra::X(), alloc), g_bar(&Spectra::Y(), alloc),
      b_bar(&Spectra::Z(), alloc), imagingRatio(imagingRatio) {
    <<Compute white balancing matrix for XYZ PixelSensor>> 
}

默认情况下，当PixelSensor转换为XYZ系数时，不会执行白平衡;该任务留给后处理。但是，如果用户指定了色温，则由XYZFromSensorRGB矩阵处理白平衡。(否则就是单位矩阵。)稍后会介绍计算该矩阵的WhiteBalance()函数。它获取两个颜色空间中白点的色度，并返回一个将第一个映射到第二个的矩阵。

<<Compute white balancing matrix for XYZ PixelSensor>>= 
if (sensorIllum) {
     Point2f sourceWhite = SpectrumToXYZ(sensorIllum).xy();
     Point2f targetWhite = outputColorSpace->w;
     XYZFromSensorRGB = WhiteBalance(sourceWhite, targetWhite);
}

像素传感器提供的主要功能是ToSensorRGB()方法，它将SampledSpectrum(采样光谱)中的点采样光谱分布 L ( λ i ) L(\lambda_i) L(λi​)转换为传感器颜色空间中的RGB系数。它通过蒙特卡罗对传感器响应积分进行评估，公式(5.6)，给出形式的估计量

r ≈ 1 n ∑ i n L ( λ i ) r ˉ ( λ i ) p ( λ i ) r\approx \frac{1}{n} \sum_i^n \frac{L(\lambda_i) \bar{r}(\lambda_i)}{p(\lambda_i)} r≈n1​i∑n​p(λi​)L(λi​)rˉ(λi​)​

其中n等于NSpectrumSamples。相关的PDF值可以从SampledWavelengths中获得，而波长之和以及除以n则使用SampledSpectrum::Average()处理。这些系数根据成像比进行缩放，从而完成转换。

<<PixelSensor Public Methods>>+= 
RGB ToSensorRGB(SampledSpectrum L,
                const SampledWavelengths &lambda) const {
    L = SafeDiv(L, lambda.PDF());
    return imagingRatio *
        RGB((r_bar.Sample(lambda) * L).Average(),
            (g_bar.Sample(lambda) * L).Average(),
            (b_bar.Sample(lambda) * L).Average());
}

Chromatic Adaptation and White Balance 色彩适应和白平衡

人类视觉系统的一个显著特性是，即使在不同的光照条件下，物体的颜色通常看起来是相同的;这种效果被称为色彩适应。照相机也有类似的功能，所以照片能捕捉到拍照的人所记得的颜色;在这种情况下，这个过程被称为白平衡。

pbrt提供了一个WhiteBalance()函数，它实现了一种称为von Kries变换的白平衡算法。它需要两个色度:一个是光照色度，另一个是白色色度。(回想4.6.3节的讨论，白色通常不是恒定光谱，而是被定义为人类认为是白色的颜色。)它返回一个3x3矩阵，对XYZ颜色应用相应的白色平衡操作。

<<White Balance Definitions>>= 
SquareMatrix<3> WhiteBalance(Point2f srcWhite, Point2f targetWhite) {
    <<Find LMS coefficients for source and target white>> 
    <<Return white balancing matrix for source and target white>> 
}

利用von Kries变换在LMS颜色空间进行白平衡，该颜色空间指定了3种匹配函数的响应度，以匹配人眼中的3种视锥。通过在LMS空间中执行白平衡，可以对调节眼睛中每种类型的锥形贡献的效果进行建模，这被认为是人类如何实现颜色适应的。在计算给定色度对应的归一化XYZ颜色后，可以使用LMSFromXYZ矩阵转换为从XYZ到LMS的转换。

<<Find LMS coefficients for source and target white>>= 
XYZ srcXYZ = XYZ::FromxyY(srcWhite), dstXYZ = XYZ::FromxyY(targetWhite);
auto srcLMS = LMSFromXYZ * srcXYZ, dstLMS = LMSFromXYZ * dstXYZ;

在LMS和XYZ之间转换的3x3矩阵可以作为常量使用。

<<Color Space Constants>>= 
extern const SquareMatrix<3> LMSFromXYZ, XYZFromLMS;

给定LMS空间中的一种颜色，通过将场景光源的颜色分开，然后乘以所需光源的颜色来实现白平衡，所需光源的颜色可以用对角矩阵表示。接下来是XYZ颜色上的完整白平衡矩阵。

<<Return white balancing matrix for source and target white>>= 
SquareMatrix<3> LMScorrect = SquareMatrix<3>::Diag(
    dstLMS[0] / srcLMS[0], dstLMS[1] / srcLMS[1], dstLMS[2] / srcLMS[2]);
return XYZFromLMS * LMScorrect * LMSFromXYZ;

图5.20显示了用黄色光源渲染的图像，以及用光源的色度进行白平衡后的图像。
在这里插入图片描述
在这里插入图片描述
图5 - 20白平衡的效果(a)具有与白炽灯泡光谱分布相似的黄色光源的场景图像。(b)白平衡图像，色温3000k。由于色彩适应，该图像比(a)更接近人类观察者看到该场景时的感知。(场景由Blend Swap提供，via Benedikt Bitterli。)

译者补充： 为什么要引入白平衡，主要原因是，人眼看到的东西并不是真实场景的样子，也是经过大脑后处理的图像。白平衡就是人眼自动处理的过程，表现为人眼具有在光照变化的情况下保持景象色彩一致的能力。比如，一朵红色的玫瑰花，在阳光下看是红色的，在阴天下你看也是红色的。

补充阅读：人眼是如何处理白平衡和色彩还原的？我感到自己眼睛在弱光条件下白平衡偏绿，这可能么？还是仅仅是我的错觉？

Sampling Sensor Response 采样传感器响应

由于 PixelSensor 使用的传感器响应函数描述传感器对辐射的波长依赖性响应，因此在对一条射线所携带的光的波长进行采样时，至少应该大致地考虑它们的变化。至少，不应该选择一个它们都为零的波长，因为这个波长对最终图像没有任何贡献。更一般地，根据传感器响应函数应用重要性抽样是可取的，因为它提供了减少方程(5.8)估计误差的可能性。

然而，选择一个用于抽样的分布是具有挑战性的，因为目标是最小化人类感知到的误差，而不是严格最小化数字误差。图5.21(a)给出了CIE Y匹配函数和X、Y、和Z匹配函数之和的图，两者都可以使用。在实际操作中，单独根据Y的采样会产生过多的色差，而三个匹配函数之和的采样会使太多的样本集中在400 nm到500 nm之间的波长，这在视觉上是相对不重要的。

一个参数概率分布函数平衡了这些问题，并很好地用于采样可见波长

p v ( λ ) = ( ∫ λ m i n λ m a x f ( λ ) d λ ) − 1 f ( λ ) p_v(\lambda) = \left ( \int_{ \lambda_{min} }^{ \lambda_{max} } f(\lambda) d\lambda \right )^{-1} f(\lambda) pv​(λ)=(∫λmin​λmax​​f(λ)dλ)−1f(λ)

并且：

f ( λ ) = 1 c o s h 2 ( A ( λ − B ) ) f(\lambda) = \frac{1}{cosh^2(A(\lambda - B))} f(λ)=cosh2(A(λ−B))1​

A = 0.0072 n m − 1 ， B = 538 n m A = 0.0072nm^{-1}，B = 538nm A=0.0072nm−1，B=538nm

图5.21(b) 显示了 p v ( λ ) p_v(\lambda) pv​(λ)

在这里插入图片描述
图5 - 21 (a) CIE Y匹配函数与X、Y、和X匹配函数之和对应的归一化PDF图。(b)方程(5.9)的参数分布图 p v ( λ ) p_v(\lambda) pv​(λ)。

我们的实现样本的波长范围从 360 n m 360nm 360nm到 830 n m 830nm 830nm。转换 f f f 为PDF的规范化常数是预先计算的。

<<Sampling Inline Functions>>+=  
Float VisibleWavelengthsPDF(Float lambda) {
    if (lambda < 360 || lambda > 830)
        return 0;
    return 0.0039398042f / Sqr(std::cosh(0.0072f * (lambda - 538)));
}

PDF可以用反演方法进行采样;结果在SampleVisibleWavelengths()中实现。

<<Sampling Inline Functions>>+=  
Float SampleVisibleWavelengths(Float u) {
    return 538 - 138.888889f * std::atanh(0.85691062f - 1.82750197f * u);
}

现在，我们可以在SampledWavelengths类中实现另一个采样方法SampleVisible()，它使用了这种技术。

<<SampledWavelengths Public Methods>>+= 
static SampledWavelengths SampleVisible(Float u) {
    SampledWavelengths swl;
    for (int i = 0; i < NSpectrumSamples; ++i) {
        <<Compute up for th wavelength sample>> 
        swl.lambda[i] = SampleVisibleWavelengths(up);
        swl.pdf[i] = VisibleWavelengthsPDF(swl.lambda[i]);
    }
    return swl;
}

与SampledWavelengths::SampleUniform()类似，SampleVisible()使用单个随机样本来生成所有波长的样本。它使用了一种稍微不同的方法，在对每个波长进行采样之前，在 [ 0 , 1 ) [0,1) [0,1)采样空间中采用均匀的步长。

<<Compute up for th wavelength sample>>= 
Float up = u + Float(i) / NSpectrumSamples;
if (up > 1)
    up -= 1;

使用这种分布代替均匀分布进行抽样是值得的。图5 - 22展示了一个场景的两幅图像，一幅使用均匀波长采样渲染，另一幅使用SampleVisible()渲染。色噪声大大减少，运行时间仅增加1%。

在这里插入图片描述

在这里插入图片描述
图5.22:(a)场景渲染，每像素4个采样，每个采样4个波长，在可见范围内均匀采样。(b)以相同的采样率渲染，但使用SampledWavelengths::SampleVisible()代替采样波长。该图像具有更少的颜色噪声，在额外的计算成本可以忽略不计。(模型由Yasutoshi Mori提供。)

5.4.3 Filtering Image Samples 滤波图像样本

Film实现的主要职责是聚合每个像素的多个光谱样本，以计算其最终值。在物理相机中，每个像素在一个小区域内集成光线。它的响应可能在该区域有一些空间变化，这取决于传感器的物理设计。在第8章中，我们将从信号处理的角度来考虑这个操作，并将看到图像函数在哪里采样以及这些样本如何加权的细节，这些细节将显著影响最终的图像质量。

在考虑这些细节之前，现在我们假设使用一些滤波函数 f f f 来定义每个图像像素周围传感器响应的空间变化。这些滤镜函数很快会归零，编码了这样一个事实:像素只对胶片上靠近它们的光线做出反应。它们还对像素响应中的任何进一步空间变化进行编码。使用这种方法，如果我们有一个图像函数 r ( x , y ) r(x,y) r(x,y)，可以在胶片上任意位置给出红色(例如，使用公式(5.6)的传感器响应函数 r ˉ ( λ ) \bar{r}(\lambda) rˉ(λ) 测量)，则滤波后 ( x , y ) (x,y) (x,y) 位置的红色值 r f r_f rf​ 为：

r f ( x , y ) = ∫ f ( x − x ′ , y − y ′ ) r ( x ′ , y ′ ) d x ′ d y ′ r_f(x,y) = \int f(x-x',y-y')r(x',y')dx'dy' rf​(x,y)=∫f(x−x′,y−y′)r(x′,y′)dx′dy′

其中假设滤波器函数 f f f 的积分为1。

像往常一样，我们将使用图像函数的点样本来估计这个积分。估计量为

r f ( x , y ) ≈ 1 n ∑ i n f ( x − x i , y − y i ) r ( x i , y i ) p ( x i , y i ) r_f(x,y) \approx \frac{1}{n} \sum_i^n \frac{ f(x-x_i,y-y_i)r(x_i,y_i)}{p(x_i,y_i)} rf​(x,y)≈n1​i∑n​p(xi​,yi​)f(x−xi​,y−yi​)r(xi​,yi​)​

在图形学中有两种方法对被积函数进行采样。第一种是对图像进行统一采样，这在之前的三个pbrt版本中都使用过。每个图像样本可能会贡献多个像素的最终值，这取决于使用的滤波器函数的范围。这种方法给出了估计器：

r f ( x , y ) ≈ A n ∑ i n f ( x − x i , y − y i ) r ( x i , y i ) r_f(x,y) \approx \frac{A}{n} \sum_i^n f(x-x_i,y-y_i)r(x_i,y_i) rf​(x,y)≈nA​i∑n​f(x−xi​,y−yi​)r(xi​,yi​)

A A A为胶片区域。图5.23说明了这个方法；它在位置 ( x , y ) (x,y) (x,y)上显示一个具有在x的方向radius.x和在y的方向radius.y范围的像素过滤器的像素。由滤波范围给出的框内 ( x i , y i ) (x_i,y_i) (xi​,yi​)位置的所有样本都可能对像素的值有贡献，这取决于滤波函数的值 f ( x − x i , y − y i ) f(x-x_i,y-y_i) f(x−xi​,y−yi​)。
在这里插入图片描述
图5.23:二维图像滤波。对于位于 ( x ， y ) (x， y) (x，y)的填充圆标记的像素，计算过滤后的像素值， ( x , y ) (x,y) (x,y)周围向外扩展 r a d i u s . x , r a d i u s . y radius.x,radius.y radius.x,radius.y的框内所有图像样本都需要被考虑 。每个图像样本(Ci, yi)，用未填充的圆表示，用一个二维滤波函数 f ( x − x i , y − y i ) f(x-x_i,y-y_i) f(x−xi​,y−yi​)加权。所有样本的加权平均值就是最终的像素值。

虽然式(5.12)给出了像素值的无偏估计，但滤波函数的变化会导致估计值的变化。考虑常量图像函数 r r r的情况:在这种情况下，我们期望得到的图像像素与 r r r完全相等。然而，过滤器值的总和 f ( x − x i , y − y i ) f(x-x_i,y-y_i) f(x−xi​,y−yi​)通常不等于1:它只期望等于1。因此，即使在这个简单的环境中，图像也会包含噪声。如果选择估计器：

r f ( x , y ) ≈ ∑ i f ( x − x i , y − y i ) r ( x i , y i ) ∑ i f ( x − x i , y − y i ) r_{\mathrm{f}}(x, y) \approx \frac{\sum_{i} f\left(x-x_{i}, y-y_{i}\right) r\left(x_{i}, y_{i}\right)}{\sum_{i} f\left(x-x_{i}, y-y_{i}\right)} rf​(x,y)≈∑i​f(x−xi​,y−yi​)∑i​f(x−xi​,y−yi​)r(xi​,yi​)​

则以少量偏差为代价消除方差。(这是加权重要性采样【weighted importance sampling】蒙特卡罗估计器。)在实践中，这种权衡是值得的。

式(5.10)也可以在每个像素独立估计。这就是这个版本的pbrt所使用的方法。在这种情况下，值得使用基于滤波函数的分布对胶片上的点进行采样。这种方法被称为滤波器重要性采样。有了它，滤波器的空间变化纯粹是通过像素的样本位置分布来考虑的，而不是根据滤波器的值缩放每个样本的贡献。

如果 p ∝ f p \propto f p∝f，那么这两个因素在方程(5.11)中相互抵消，我们得到的是按比例常数缩放的样本值 r ( x i , y i ) r(x_i,y_i) r(xi​,yi​)的平均值。但是，在这里我们必须处理罕见的情况(对于渲染来说):估计一个积分可能是负的:我们将在第8章中看到，部分为负的滤波器函数可以比非负的函数提供更好的结果。在这种情况下，我们有 p ∝ ∣ f ∣ p \propto |f| p∝∣f∣，它提供：
r f ( x , y ) ≈ ( ∫ ∣ f ( x ′ , y ′ ) ∣ d x ′ d y ′ ) ( 1 n ∑ i n sign ⁡ ( f ( x − x i , y − y i ) ) r ( x i , y i ) ) r_{\mathrm{f}}(x, y) \approx\left(\int\left|f\left(x^{\prime}, y^{\prime}\right)\right| \mathrm{d} x^{\prime} \mathrm{d} y^{\prime}\right)\left(\frac{1}{n} \sum_{i}^{n} \operatorname{sign}\left(f\left(x-x_{i}, y-y_{i}\right)\right) r\left(x_{i}, y_{i}\right)\right) rf​(x,y)≈(∫∣f(x′,y′)∣dx′dy′)(n1​i∑n​sign(f(x−xi​,y−yi​))r(xi​,yi​))

如果 x > 0 x>0 x>0 则 s i g n ( x ) = 1 sign(x)=1 sign(x)=1，
如果 x = 0 x=0 x=0 则 s i g n ( x ) = 0 sign(x)=0 sign(x)=0，
如果 x < 0 x<0 x<0 则 s i g n ( x ) = − 1 sign(x)=-1 sign(x)=−1

然而，这个估计器有与公式(5.12)相同的问题:即使是常数函数 r r r，估计也会有方差，这取决于有多少 s i g n sign sign 函数评估给出 1 1 1，有多少给出 − 1 -1 −1。

因此，这个版本的pbrt继续使用加权重要性采样估计器，计算像素值为

r f ( x , y ) ≈ ∑ i w ( x − x i , y − y i ) r ( x i , y i ) ∑ i w ( x − x i , y − y i ) r_{\mathrm{f}}(x, y) \approx \frac{\sum_{i} w\left(x-x_{i}, y-y_{i}\right) r\left(x_{i}, y_{i}\right)}{\sum_{i} w\left(x-x_{i}, y-y_{i}\right)} rf​(x,y)≈∑i​w(x−xi​,y−yi​)∑i​w(x−xi​,y−yi​)r(xi​,yi​)​

其中 ω ( x , y ) = f ( x , y ) / p ( x , y ) \omega(x,y) = f(x,y)/p(x,y) ω(x,y)=f(x,y)/p(x,y).

这两种方法中的第一个具有优势：每个图像样本可以贡献多个像素的最终滤波值。这有助于提高渲染效率，因为计算图像样本的辐射度所涉及的所有计算都可以用于提高多个像素的精度。然而，使用为其他像素生成的样本并不总是有用的:第8章实现的一些样本生成算法会仔细地定位样本，以确保良好地覆盖某个像素的采样域。如果来自其他像素的样本与这些样本混合在一起，一个像素的完整样本集可能不再具有相同的结构，这反过来会增加误差。通过不跨像素共享样本，滤波器重要性采样就不会有这个问题。

滤波器重要性采样还有其他优点。它使并行渲染更容易:如果渲染器以一种让不同线程处理不同像素的方式并行化，就永远不会有需要多个线程并发修改相同像素值的机会。最后一个优点是，如果有任何样本由于采样不佳的被积函数产生的方差峰值而比其他样本亮得多，那么这些样本只对单个像素有贡献，而不是被涂抹在多个像素上。修复由此产生的单像素伪影比修复受该样本影响的它们的邻域更容易。

5.4.4 The Film Interface 胶片接口

在建立了传感器响应和像素采样滤波的基础上，我们可以引入Film接口。它在base/film.h文件中定义。

<<Film Definition>>= 
class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
  public:
    <<Film Interface>> 
};

SpectralFilm，这里没有描述，记录特定波长范围内的光谱图像，该波长范围被离散到不重叠的范围。有关SpectralFilm使用的更多信息，请参阅pbrt文件格式的文档。

样品可以通过两种方式提供给胶片。第一个是采样器在胶片上选择点，积分器在这些点上估计辐射度。AddSample()方法为Film提供了这些示例，该方法接受下列参数。

  • 样本的像素坐标， p F i l m pFilm pFilm。
  • 样品的光谱辐亮度， L L L。
  • 样品的波长 λ λ λ。
  • 一种可选的VisibleSurface，描述了沿样品的相机射线的第一个可见点的几何形状。
  • 计算式(5.13)中样本的权重，由Filter::Sample().返回。

Film实现可以假设多个线程不会对同一个pFilm位置同时调用AddSample()(尽管它们应该假设多个线程会对不同的pFilm位置同时调用它)。因此，在这种方法的实现中，无需担心互斥问题，除非修改了某个像素的非唯一数据。

<<Film Interface>>= 
void AddSample(Point2i pFilm, SampledSpectrum L,
    const SampledWavelengths &lambda,
    const VisibleSurface *visibleSurface, Float weight);

Film接口还包括一个方法，该方法返回可能生成的所有样本的边界框。请注意，这与图像像素的边界框不同，通常像素滤波器的范围大于一个像素。

<<Film Interface>>+=  
Bounds2f SampleBounds() const;

VisibleSurface 保存了关于表面上一个点的各种信息。

<<VisibleSurface Definition>>= 
class VisibleSurface {
public:
    <<VisibleSurface Public Methods>> 
    <<VisibleSurface Public Members>> 
};

除了点、法线、渲染法线和时间，VisibleSurface还存储了在每个像素处深度的偏导数， ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z​ 以及 ∂ z ∂ y \frac{\partial z}{\partial y} ∂y∂z​，其中x和y在栅格空间中，z在相机空间中。这些值在图像去噪算法中很有用，因为它们使得检测相邻像素内的表面是否共面成为可能。表面反照率是均匀光照下反射光的光谱分布;这个量可以在去噪前将纹理从光照中分离出来。

class VisibleSurface {
public:
    <<VisibleSurface Public Methods>> 
    
    // <<VisibleSurface Public Members>> 
    Point3f p;
	Normal3f n, ns;
	Point2f uv;
	Float time = 0;
	Vector3f dpdx, dpdy;
	SampledSpectrum albedo;
};

这里我们将不包括VisibleSurface 构造函数，因为它的主要功能是从SurfaceInteraction中将适当的值复制到它的成员变量中。

class VisibleSurface {
public:
    // <<VisibleSurface Public Methods>> 
    VisibleSurface(	const SurfaceInteraction &si, 
	    			SampledSpectrum albedo,
               		const SampledWavelengths &lambda);
    // <<VisibleSurface Public Members>> 
    Point3f p;
	Normal3f n, ns;
	Point2f uv;
	Float time = 0;
	Vector3f dpdx, dpdy;
	SampledSpectrum albedo;
};

set成员变量表示是否初始化了一个VisibleSurface。

class VisibleSurface {
public:
    // <<VisibleSurface Public Methods>> 
    VisibleSurface(	const SurfaceInteraction &si, 
	    			SampledSpectrum albedo,
               		const SampledWavelengths &lambda);

	operator bool() const { return set; }
	
    // <<VisibleSurface Public Members>> 
    Point3f p;
	Normal3f n, ns;
	Point2f uv;
	Float time = 0;
	Vector3f dpdx, dpdy;
	SampledSpectrum albedo;

	bool set = false;
};

Film实现可以通过UsesVisibleSurface()表示是否使用了传递给AddSample()方法的VisibleSurface *。提供这些信息可以让积分器在不使用可见表面的情况下跳过初始化的开销。

class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
public:
    <<Film Interface>> 
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *visibleSurface, Float weight);
    Bounds2f SampleBounds() const;
    bool UsesVisibleSurface() const;

};

从光源开始采样路径的光传输算法(例如双向路径，要求能够对任意像素进行“splat”【这里splat应该是光子的意思】贡献。不是将最终像素值计算为所贡献的光子的加权平均值，而是简单地对光子进行求和。一般来说，给定像素周围的光子越多，该像素就越亮。AddSplat()将给定的值光子映射【splats】到图像中的指定位置。

与AddSample()不同的是，这个方法可以被多个线程并发调用，并且最终更新的是同一个像素。因此，Film的实现必须要么实现某种形式的互斥，要么在实现该方法时使用原子操作。

class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
public:
    <<Film Interface>> 
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *visibleSurface, Float weight);
    Bounds2f SampleBounds() const;
    bool UsesVisibleSurface() const;
    void AddSplat(Point2f p, SampledSpectrum v,
              const SampledWavelengths &lambda);

};

Film的实现还必须提供SampleWavelengths()方法，该方法根据Film传感器响应的波长范围进行采样(例如，使用SampledWavelengths::SampleVisible())。

class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
public:
    <<Film Interface>> 
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *visibleSurface, Float weight);
    Bounds2f SampleBounds() const;
    bool UsesVisibleSurface() const;
    void AddSplat(Point2f p, SampledSpectrum v,
              const SampledWavelengths &lambda);
    SampledWavelengths SampleWavelengths(Float u) const;

};

此外，他们必须提供一些方法来给出图像的范围和传感器的对角线长度，以米为单位。

class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
public:
    <<Film Interface>> 
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *visibleSurface, Float weight);
    Bounds2f SampleBounds() const;
    bool UsesVisibleSurface() const;
    void AddSplat(Point2f p, SampledSpectrum v,
              const SampledWavelengths &lambda);
    SampledWavelengths SampleWavelengths(Float u) const;

	Point2i FullResolution() const;
	Bounds2i PixelBounds() const;
	Float Diagonal() const;

};

调用Film::WriteImage()方法，让Film进行必要的处理，生成最终的图像，并将其存储在文件中。除了camera变换外，这个方法还需要一个缩放因子，该因子会应用到AddSplat()方法提供的样本上。

class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
public:
    <<Film Interface>> 
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *visibleSurface, Float weight);
    Bounds2f SampleBounds() const;
    bool UsesVisibleSurface() const;
    void AddSplat(Point2f p, SampledSpectrum v,
              const SampledWavelengths &lambda);
    SampledWavelengths SampleWavelengths(Float u) const;

	Point2i FullResolution() const;
	Bounds2i PixelBounds() const;
	Float Diagonal() const;

	void WriteImage(ImageMetadata metadata, Float splatScale = 1);
};

ToOutputRGB()方法允许调用者根据给定的光谱辐射度样本，应用PixelSensor模型，执行白平衡，然后转换到输出颜色空间，从而得到输出的RGB值。(在线版中的SPPMIntegrator使用这个方法，它要求维护最终图像本身，而不是使用Film实现。)

class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
public:
    <<Film Interface>> 
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *visibleSurface, Float weight);
    Bounds2f SampleBounds() const;
    bool UsesVisibleSurface() const;
    void AddSplat(Point2f p, SampledSpectrum v,
              const SampledWavelengths &lambda);
    SampledWavelengths SampleWavelengths(Float u) const;

	Point2i FullResolution() const;
	Bounds2i PixelBounds() const;
	Float Diagonal() const;

	void WriteImage(ImageMetadata metadata, Float splatScale = 1);
	RGB ToOutputRGB(SampledSpectrum L, const SampledWavelengths &lambda) const;
};

调用者还可以请求返回整个图像，以及单个像素的RGB值。后一种方法用于在渲染期间显示正在进行的图像。

class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
public:
    <<Film Interface>> 
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *visibleSurface, Float weight);
    Bounds2f SampleBounds() const;
    bool UsesVisibleSurface() const;
    void AddSplat(Point2f p, SampledSpectrum v,
              const SampledWavelengths &lambda);
    SampledWavelengths SampleWavelengths(Float u) const;

	Point2i FullResolution() const;
	Bounds2i PixelBounds() const;
	Float Diagonal() const;

	void WriteImage(ImageMetadata metadata, Float splatScale = 1);
	RGB ToOutputRGB(SampledSpectrum L, const SampledWavelengths &lambda) const;

	Image GetImage(ImageMetadata *metadata, Float splatScale = 1);
	RGB GetPixelRGB(Point2i p, Float splatScale = 1) const;
};

最后，Film实现必须提供对一些附加值的访问，以便在系统的其他部分使用。

class Film : public TaggedPointer<RGBFilm, GBufferFilm, SpectralFilm> {
public:
    <<Film Interface>> 
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *visibleSurface, Float weight);
    Bounds2f SampleBounds() const;
    bool UsesVisibleSurface() const;
    void AddSplat(Point2f p, SampledSpectrum v,
              const SampledWavelengths &lambda);
    SampledWavelengths SampleWavelengths(Float u) const;

	Point2i FullResolution() const;
	Bounds2i PixelBounds() const;
	Float Diagonal() const;

	void WriteImage(ImageMetadata metadata, Float splatScale = 1);
	RGB ToOutputRGB(SampledSpectrum L, const SampledWavelengths &lambda) const;

	Image GetImage(ImageMetadata *metadata, Float splatScale = 1);
	RGB GetPixelRGB(Point2i p, Float splatScale = 1) const;

	Filter GetFilter() const;
	const PixelSensor *GetPixelSensor() const;
	std::string GetFilename() const;
};

5.4.5 Common Film Functionality 常用胶片功能

正如我们为Camera实现使用CameraBase一样，我们已经编写了一个FilmBase类，Film实现可以从它继承。它收集常用的成员变量，并能够提供Film接口所需的一些方法。

class FilmBase {
  public:
    <<FilmBase Public Methods>> 
  protected:
    <<FilmBase Protected Members>> 
};

FilmBase构造函数接受一系列值:图像的整体分辨率(以像素为单位)；一个边界框，可以指定整个图像的一个子集；滤波函数；PixelSensor；胶片物理面积的对角线长度；以及输出图像的文件名。这些都被打包成一个小的结构，以便缩短即将到来的构造函数的参数列表。

struct FilmBaseParameters {
    Point2i fullResolution;
    Bounds2i pixelBounds;
    Filter filter;
    Float diagonal;
    const PixelSensor *sensor;
    std::string filename;
};

FilmBase构造函数之后复制参数结构中的各种值，将胶片对角线长度从毫米(在场景描述文件中指定)转换为米(在pbrt中用于测量距离的单位)。

class FilmBase {
  public:
    // <<FilmBase Public Methods>> 
    FilmBase(FilmBaseParameters p)
	    : fullResolution(p.fullResolution), pixelBounds(p.pixelBounds),
	      filter(p.filter), diagonal(p.diagonal * .001f), sensor(p.sensor),
	      filename(p.filename) {
	}
  protected:
    // <<FilmBase Protected Members>> 
    Point2i fullResolution;
	Bounds2i pixelBounds;
	Filter filter;
	Float diagonal;
	const PixelSensor *sensor;
	std::string filename;
};

有了这些值，就可以立即实现Film接口所需的许多方法。

	<<FilmBase Public Methods>>+=  
	Point2i FullResolution() const { return fullResolution; }
	Bounds2i PixelBounds() const { return pixelBounds; }
	Float Diagonal() const { return diagonal; }
	Filter GetFilter() const { return filter; }
	const PixelSensor *GetPixelSensor() const { return sensor; }
	std::string GetFilename() const { return filename; }

SampleWavelengths() 的实现按照式(5.9)中的分布进行采样。

	<<FilmBase Public Methods>>+= 
	SampledWavelengths SampleWavelengths(Float u) const {
	    return SampledWavelengths::SampleVisible(u);
	}

给出Filter, Film::SampleBounds()方法也可以很容易地实现。计算样本边界涉及到扩展滤波器半径和计算来自pbrt中用于像素坐标的半像素偏移;第8.1.4节将对此进行更详细的解释。

<<FilmBase Method Definitions>>= 
Bounds2f FilmBase::SampleBounds() const {
    Vector2f radius = filter.Radius();
    return Bounds2f(pixelBounds.pMin - radius + Vector2f(0.5f, 0.5f),
                    pixelBounds.pMax + radius - Vector2f(0.5f, 0.5f));
}

5.4.6 RGBFilm

RGBFilm 记录用RGB颜色表示的图像。

<<RGBFilm Definition>>= 
class RGBFilm : public FilmBase {
  public:
    <<RGBFilm Public Methods>> 
  private:
    <<RGBFilm::Pixel Definition>> 
    <<RGBFilm Private Members>> 
};

除了传递给FilmBase的参数之外，RGBFilm还需要一个用于输出图像的颜色空间、一个允许指定RGB颜色组件最大值的参数，以及一个控制输出图像中的浮点精度的参数。

<<RGBFilm Method Definitions>>= 
RGBFilm::RGBFilm(FilmBaseParameters p, const RGBColorSpace *colorSpace,
                 Float maxComponentValue, bool writeFP16, Allocator alloc)
    : FilmBase(p), pixels(p.pixelBounds, alloc), colorSpace(colorSpace),
      maxComponentValue(maxComponentValue), writeFP16(writeFP16) {
    filterIntegral = filter.Integral();
    <<Compute outputRGBFromSensorRGB matrix>> 
}

过滤器函数的积分对于规一化过滤器值很有用，过滤器值用于AddSplat()提供的样本，因此它被缓存在成员变量中。

<<RGBFilm Private Members>>= 
const RGBColorSpace *colorSpace;
Float maxComponentValue;
bool writeFP16;
Float filterIntegral;

最终图像的颜色空间由用户指定的RGBColorSpace给出，它不太可能与传感器的RGB颜色空间相同。构造函数因此计算一个3x3矩阵，将传感器RGB值转换为输出颜色空间。

<<RGBFilm Method Definitions>>= 
RGBFilm::RGBFilm(FilmBaseParameters p, const RGBColorSpace *colorSpace,
                 Float maxComponentValue, bool writeFP16, Allocator alloc)
    : FilmBase(p), pixels(p.pixelBounds, alloc), colorSpace(colorSpace),
      maxComponentValue(maxComponentValue), writeFP16(writeFP16) {
    filterIntegral = filter.Integral();
    // <<Compute outputRGBFromSensorRGB matrix>> 
    outputRGBFromSensorRGB = colorSpace->RGBFromXYZ * sensor->XYZFromSensorRGB;
}

<<RGBFilm Private Members>>= 
const RGBColorSpace *colorSpace;
Float maxComponentValue;
bool writeFP16;
Float filterIntegral;

SquareMatrix<3> outputRGBFromSensorRGB;

给定图像(可能裁剪)的像素分辨率，构造函数分配一个像素结构的2D数组，每个像素一个。在rgbSum成员变量中使用RGB颜色表示像素贡献的运行加权和。weightSum保存样本对像素贡献的过滤器权重值的总和。分别对应式(5.13)中的分子和分母。最后，rgbSplat保存样本splat的(未加权的)和。

所有这些量都使用双精度浮点。单精度浮点数几乎总是足够的，但当用于参考图像渲染的高样本计数时，它们可能没有足够的精度来准确地存储相关的和。虽然这种误差很少在视觉上很明显，但它会对用于评估蒙特卡洛采样算法误差的参考图像造成问题。

图5 - 24展示了这个问题的一个例子。我们在每个像素中使用400万个样本渲染测试场景的参考图像，使用32位和64位浮点值作为RGBFilm像素值。然后，我们绘制了均方误差(MSE)作为样本计数的函数。对于无偏蒙特卡洛估计，MSE在采样的数量为n时为 O ( 1 / n ) O(1/n) O(1/n);在对数图中，它应该是一条斜率为 − 1 -1 −1的直线。然而，我们可以看到，对于一个 n > 1000 n>1000 n>1000 的32位浮点参考图像，MSE的减少似乎是扁平化的，更多的样本似乎并没有减少误差。对于64位浮点数，曲线保持其预期路径。

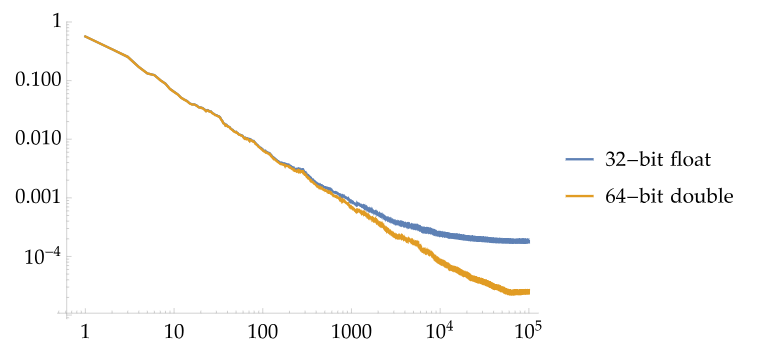
在这里插入图片描述
图5.24:均方误差作为样本数量的函数。当使用无偏蒙特卡罗估计器渲染场景时，我们期望MSE以 O ( 1 / n ) O(1/n) O(1/n) 与样本数量n相关。在对数-对数图中，这个速率对应于一条斜率为-1的直线。对于这里考虑的测试场景，我们可以看到，对参考图像使用32位浮点数会导致报告的错误，即在1000个左右的样本后不正确地停止减少误差。

<<RGBFilm Definition>>= 
class RGBFilm : public FilmBase {
public:
    // <<RGBFilm Public Methods>> 
    RGB GetPixelRGB(Point2i p, Float splatScale = 1) const {
        const Pixel &pixel = pixels[p];
        RGB rgb(pixel.rgbSum[0], pixel.rgbSum[1], pixel.rgbSum[2]);
        <<Normalize rgb with weight sum>> 
        <<Add splat value at pixel>> 
        <<Convert rgb to output RGB color space>> 
        return rgb;
    }
    RGBFilm(FilmBaseParameters p, const RGBColorSpace *colorSpace, Float maxComponentValue = Infinity,
            bool writeFP16 = true, Allocator alloc = {});

private:
    // <<RGBFilm::Pixel Definition>> 
    struct Pixel {
	    double rgbSum[3] = {0., 0., 0.};
	    double weightSum = 0.;
	    AtomicDouble rgbSplat[3];
	};
	
    <<RGBFilm Private Members>> 
    const RGBColorSpace *colorSpace;
    Float maxComponentValue;
    bool writeFP16;
    Float filterIntegral;
    SquareMatrix<3> outputRGBFromSensorRGB;
    Array2D<Pixel> pixels;
};

RGBFilm不使用传递给AddSample()的VisibleSurface * 。

AddSample()在更新点pFilm对应的像素之前将光谱亮度转换为传感器RGB。

<<RGBFilm Definition>>= 
class RGBFilm : public FilmBase {
public:
    // <<RGBFilm Public Methods>> 
    bool UsesVisibleSurface() const { return false; }
    void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *, Float weight) {
        <<Convert sample radiance to PixelSensor RGB>>  
        <<Optionally clamp sensor RGB value>> 
        <<Update pixel values with filtered sample contribution>> 
    }
    RGB GetPixelRGB(Point2i p, Float splatScale = 1) const {
        const Pixel &pixel = pixels[p];
        RGB rgb(pixel.rgbSum[0], pixel.rgbSum[1], pixel.rgbSum[2]);
        <<Normalize rgb with weight sum>> 
        <<Add splat value at pixel>> 
        <<Convert rgb to output RGB color space>> 
        return rgb;
    }
    RGBFilm(FilmBaseParameters p, const RGBColorSpace *colorSpace, Float maxComponentValue = Infinity,
            bool writeFP16 = true, Allocator alloc = {});

private:
    // <<RGBFilm::Pixel Definition>> 
    struct Pixel {
	    double rgbSum[3] = {0., 0., 0.};
	    double weightSum = 0.;
	    AtomicDouble rgbSplat[3];
	};
	
    <<RGBFilm Private Members>> 
    const RGBColorSpace *colorSpace;
    Float maxComponentValue;
    bool writeFP16;
    Float filterIntegral;
    SquareMatrix<3> outputRGBFromSensorRGB;
    Array2D<Pixel> pixels;
};

亮度值首先由传感器转换为RGB。

<<RGBFilm Public Methods>>+= 
void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *, Float weight) {
    // <<Convert sample radiance to PixelSensor RGB>>  
    RGB rgb = sensor->ToSensorRGB(L, lambda);
    <<Optionally clamp sensor RGB value>> 
    <<Update pixel values with filtered sample contribution>> 
}

使用蒙特卡罗积分渲染的图像，如果使用的采样分布与被积函数不匹配，则可以在像素中显示出明亮的噪声峰值，因此当在蒙特卡罗估计器中计算 f ( x ) / p ( x ) f(x)/p(x) f(x)/p(x)时， f ( x ) f(x) f(x)非常大， p ( x ) p(x) p(x)非常小。(这样的像素通常被称为“ fireflies (萤火虫)”)可能需要许多额外的样本来获得该像素的准确估计。

减少萤火虫影响的一种广泛使用的技术是将所有样品的贡献限制在某个最大值。这样做会带来误差:能量损失，图像不再是真实图像的无偏估计。然而，当渲染图像的美学比它们的数学更重要时，这可能是一个有用的补救措施。图5.25显示了它的使用示例。
在这里插入图片描述
在这里插入图片描述
图5.25:在某些像素中具有高方差的图像。由于难以采样的光路偶尔会与太阳相交，这个场景遭受了像素的方差峰值。(a)正常渲染的图像。(b)clamping渲染的图像，其中像素样本RGB值被限制，其值不大于10。虽然以能量损失为代价，但限制后的图像看起来要好得多。(模型由 Yasutoshi Mori 提供。)

RGBFilm的maxComponentValue参数可以设置为用于限制的阈值。默认情况下，它是无限的，并且不执行限制。

<<RGBFilm Public Methods>>+= 
void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *, Float weight) {
    // <<Convert sample radiance to PixelSensor RGB>>  
    RGB rgb = sensor->ToSensorRGB(L, lambda);
    // <<Optionally clamp sensor RGB value>> 
    Float m = std::max({rgb.r, rgb.g, rgb.b});
	if (m > maxComponentValue)
	    rgb *= maxComponentValue / m;
    <<Update pixel values with filtered sample contribution>> 
}

给定可能被限制的RGB值， 通过将其贡献添加到方程(5.13)的分子和分母的运行求和，可以更新它所在的像素。

<<RGBFilm Public Methods>>+= 
void AddSample(Point2i pFilm, SampledSpectrum L,
           const SampledWavelengths &lambda,
           const VisibleSurface *, Float weight) {
    // <<Convert sample radiance to PixelSensor RGB>>  
    RGB rgb = sensor->ToSensorRGB(L, lambda);
    // <<Optionally clamp sensor RGB value>> 
    Float m = std::max({rgb.r, rgb.g, rgb.b});
	if (m > maxComponentValue)
	    rgb *= maxComponentValue / m;
    // <<Update pixel values with filtered sample contribution>> 
	Pixel &pixel = pixels[pFilm];
	for (int c = 0; c < 3; ++c)
	    pixel.rgbSum[c] += weight * rgb[c];
	pixel.weightSum += weight;
}

AddSplat()方法首先重用来自AddSample()的前两个片段来计算提供的亮度L的RGB值。

<<RGBFilm Method Definitions>>+= 
void RGBFilm::AddSplat(Point2f p, SampledSpectrum L,
                       const SampledWavelengths &lambda) {
    <<Convert sample radiance to PixelSensor RGB>> 
    <<Optionally clamp sensor RGB value>> 
    <<Compute bounds of affected pixels for splat, splatBounds>> 
    for (Point2i pi : splatBounds) {
        <<Evaluate filter at pi and add splat contribution>> 
    }
}

由于splatted贡献不是像素样本的结果，而是场景中投影到film平面上的点，因此有必要考虑它们对多个像素的贡献，因为每个像素的重建滤波器通常会向外扩展，以包括附近像素的贡献。

首先，使用过滤器的半径找到潜在受影响像素的边界框。参见第8.1.4节，其中解释了在pbrt中索引像素的约定，特别是在这里添加 ( 0.5 , 0.5 ) (0.5,0.5) (0.5,0.5)像素坐标。

<<RGBFilm Method Definitions>>+= 
void RGBFilm::AddSplat(Point2f p, SampledSpectrum L,
                       const SampledWavelengths &lambda) {
    <<Convert sample radiance to PixelSensor RGB>> 
    <<Optionally clamp sensor RGB value>> 
    // <<Compute bounds of affected pixels for splat, splatBounds>> 
	Point2f pDiscrete = p + Vector2f(0.5, 0.5);
	Vector2f radius = filter.Radius();
	Bounds2i splatBounds(Point2i(Floor(pDiscrete - radius)),
	                     Point2i(Floor(pDiscrete + radius)) + Vector2i(1, 1));
	splatBounds = Intersect(splatBounds, pixelBounds);
	
    for (Point2i pi : splatBounds) {
        <<Evaluate filter at pi and add splat contribution>> 
    }
}

如果过滤器权重非零，则添加splat的加权贡献。与AddSample()不同，没有维护过滤器权重的总和；稍后使用过滤器的积分处理归一化，如式(5.10)所示。

<<RGBFilm Method Definitions>>+= 
void RGBFilm::AddSplat(Point2f p, SampledSpectrum L,
                       const SampledWavelengths &lambda) {
    <<Convert sample radiance to PixelSensor RGB>> 
    <<Optionally clamp sensor RGB value>> 
    // <<Compute bounds of affected pixels for splat, splatBounds>> 
	Point2f pDiscrete = p + Vector2f(0.5, 0.5);
	Vector2f radius = filter.Radius();
	Bounds2i splatBounds(Point2i(Floor(pDiscrete - radius)),
	                     Point2i(Floor(pDiscrete + radius)) + Vector2i(1, 1));
	splatBounds = Intersect(splatBounds, pixelBounds);
	
    for (Point2i pi : splatBounds) {
        // <<Evaluate filter at pi and add splat contribution>> 
		Float wt = filter.Evaluate(Point2f(p - pi - Vector2f(0.5, 0.5)));
		if (wt != 0) {
		    Pixel &pixel = pixels[pi];
		    for (int i = 0; i < 3; ++i)
		        pixel.rgbSplat[i].Add(wt * rgb[i]);
		}
    }
}

GetPixelRGB()返回RGBFilm输出色彩空间中给定像素的最终RGB值。

<<RGBFilm Public Methods>>+=  
RGB GetPixelRGB(Point2i p, Float splatScale = 1) const {
    const Pixel &pixel = pixels[p];
    RGB rgb(pixel.rgbSum[0], pixel.rgbSum[1], pixel.rgbSum[2]);
    <<Normalize rgb with weight sum>> 
    <<Add splat value at pixel>> 
    <<Convert rgb to output RGB color space>> 
    return rgb;
}

首先，通过公式(5.13)计算AddSample()提供的值的最终像素贡献。

RGB GetPixelRGB(Point2i p, Float splatScale = 1) const {
    const Pixel &pixel = pixels[p];
    RGB rgb(pixel.rgbSum[0], pixel.rgbSum[1], pixel.rgbSum[2]);
    // <<Normalize rgb with weight sum>> 
    Float weightSum = pixel.weightSum;
    if (weightSum != 0)
        rgb /= weightSum;

    <<Add splat value at pixel>> 
    <<Convert rgb to output RGB color space>> 
    return rgb;
}

然后可以应用公式(5.10)来合并任何光子的值。

RGB GetPixelRGB(Point2i p, Float splatScale = 1) const {
    const Pixel &pixel = pixels[p];
    RGB rgb(pixel.rgbSum[0], pixel.rgbSum[1], pixel.rgbSum[2]);
    // <<Normalize rgb with weight sum>> 
    Float weightSum = pixel.weightSum;
    if (weightSum != 0)
        rgb /= weightSum;

    // <<Add splat value at pixel>> 
    for (int c = 0; c < 3; ++c)
    	rgb[c] += splatScale * pixel.rgbSplat[c] / filterIntegral;
    	
    <<Convert rgb to output RGB color space>> 
    return rgb;
}

最后，颜色转换矩阵将RGB值带入输出颜色空间。

RGB GetPixelRGB(Point2i p, Float splatScale = 1) const {
    const Pixel &pixel = pixels[p];
    RGB rgb(pixel.rgbSum[0], pixel.rgbSum[1], pixel.rgbSum[2]);
    // <<Normalize rgb with weight sum>> 
    Float weightSum = pixel.weightSum;
    if (weightSum != 0)
        rgb /= weightSum;

    // <<Add splat value at pixel>> 
    for (int c = 0; c < 3; ++c)
    	rgb[c] += splatScale * pixel.rgbSplat[c] / filterIntegral;
    	
    // <<Convert rgb to output RGB color space>> 
    rgb = outputRGBFromSensorRGB * rgb;
    return rgb;
}

ToOutputRGB()的实现首先使用传感器计算传感器RGB，然后转换为输出颜色空间。

<<RGBFilm Public Methods>>+= 
RGB ToOutputRGB(SampledSpectrum L, const SampledWavelengths &lambda) const {
    RGB sensorRGB = sensor->ToSensorRGB(L, lambda);
    return outputRGBFromSensorRGB * sensorRGB;
}

我们不会在书中包括直接的RGBFilm WriteImage()或GetImage()方法实现。前者在调用Image::Write()之前调用GetImage()，后者使用GetPixelRGB()填充图像以获取每个像素的值。

5.4.7 GBufferFilm

GBufferFilm不仅在每个像素上存储RGB，而且在第一个可见交叉点上存储有关几何形状的附加信息。这些额外的信息对各种应用都很有用，从图像去噪算法到为机器学习应用提供训练数据。

<<GBufferFilm Definition>>= 
class GBufferFilm : public FilmBase {
  public:
    <<GBufferFilm Public Methods>> 
  private:
    <<GBufferFilm::Pixel Definition>> 
    <<GBufferFilm Private Members>> 
};

我们将不包括任何GBufferFilm实现，除了它的Pixel结构，它增加了RGBFilm中使用的存储几何信息的附加字段。它还使用VarianceEstimator类(在章节B.2.11中定义)存储每个像素上红色、绿色和蓝色值的方差估计。实现的其余部分是RGBFilm的直接泛化，它也更新这些附加值。

<<GBufferFilm::Pixel Definition>>= 
struct Pixel {
    double rgbSum[3] = {0., 0., 0.};
    double weightSum = 0., gBufferWeightSum = 0.;
    AtomicDouble rgbSplat[3];
    Point3f pSum;
    Float dzdxSum = 0, dzdySum = 0;
    Normal3f nSum, nsSum;
    Point2f uvSum;
    double rgbAlbedoSum[3] = {0., 0., 0.};
    VarianceEstimator<Float> rgbVariance[3];
};
【代码解读】1. 处理命令行参数 - Physically Based Rendering From Theory To Implementation(PBRT)
Elsa的迷弟
03-15 973
该系列属于系统源代码解读系列，根据源码程序，分析程序处理路径，从系统层面探索基于物理的渲染的奥秘。该系列为译者原创，转载请说明原文出处。作者：Elsa的迷弟个人blog网址：https://blog.csdn.net/weixin_44518102。
1.6 深入阅读 - Physically Based Rendering From Theory To Implementation(PBRT)
Elsa的迷弟
02-17 184
他们包括Burley等人对迪士尼的Hyperion渲染器(2018)的描述，Christensen等人对皮克斯的现代渲染器(2018)的描述，Fascione等人对维塔数字公司的Manuka(2018)的描述，Georgiev等人对立体角版本的Arnold(2018)的描述，以及Kulla等人对Sony Pictures Imageworks使用的Arnold(2018)的描述。在一篇关于光线追踪系统设计的论文中，Kirk和Arvo(1988)提出了许多原则，这些原则现在已经成为渲染器设计的经典。
Physically Based Rendering. From Theory to Implementation
06-23
[Morgan Kaufmann series in computer graphics and geometric modeling] Matt Pharr, Wenzel Jakob, Greg Humphreys - Physically Based Rendering. From Theory to Implementation (2017, Morgan Kaufmann)
Physically-Based Rendering - From Theory To Implementation .pdf
02-17
对于理解渲染的各个部分，构建渲染器很有用，特别是在体渲染方面，提供了很详细的介绍。
6.7 曲线 - Physically Based Rendering From Theory To Implementation(PBRT)
Elsa的迷弟
03-13 234
翻译：https://pbr-book.org/4ed/Shapes/Curves总目录： Physically Based Rendering From Theory To Implementation - 基于物理的渲染从理论到实践第四版原书翻译虽然三角形或双直线曲面分块（bilinear patches）可以用来表示细形状，以建模精细的几何形状，如头发、毛皮或草地，但为了更有效地渲染这些对象，有必要使用专门的形状，因为它们通常存在许多单独的实例。本节介绍的曲线形状表示用三次Bézier曲线建模的薄几何
Physically Based Rendering: From Theory to Implementation源代码
03-15
《Physically Based Rendering: From Theory to Implementation》第三版的配套源代码。
6.1 基本Shape接口 - Physically Based Rendering From Theory To Implementation(PBRT)
Elsa的迷弟
03-07 185
翻译：https://pbr-book.org/4ed/Shapes/Basic_Shape_Interface总目录： Physically Based Rendering From Theory To Implementation - 基于物理的渲染从理论到实践第四版原书翻译shape的接口在文件中定义，shape的实现可以在和中找到。Shape类定义了通用的形状接口。【本章内所有的Shape都翻译为形状】 6.1.1 Bounding pbrt渲染的场景通常包含处理计算开销很大的对象。对于许多操作，使
Physically-Based.Rendering.-.From.Theory.To.Implementation.pdf
03-19
#### 胶片与成像管道 胶片和成像管道是渲染流程中的核心组件，负责将光线信息转化为可见图像。书中介绍了胶片接口的概念，以及如何通过图像胶片来存储和处理光线信息。同时，深入探讨了感知问题和色调映射技术，...
Physically Based Rendering from Theory to Implementation - part1
03-01
Physically Based Rendering from Theory to Implementation 一共3部分～～～～～～～～～, 源码下载to h t t p ://www.p b r t . o r g /downloads.php /////////////////////////////////// CHAPTER 01. ...
5.1摄像头接口 - Physically Based Rendering From Theory To Implementation(PBRT)
Elsa的迷弟
03-05 183
反过来，如果相机相对于场景旋转，轴对齐的边界框在边界这些特征方面的效果会更差，渲染性能会受到影响:对于图5 - 1中的场景，渲染时间增加了27%。关于相机光线如何作为胶片上位置的函数而变化的信息，有助于给系统的其他部分一个概念，即特定相机光线的样本代表了多少胶片区域，这对于反走样纹理查找很有用。简单的相机模型将权重保留为默认值1，而更复杂的相机模型，如RealisticCamera，返回一个用于图像形成的辐射度建模的权重。在这种情况下，相机空间是一个方便的空间，用于推理哪些对象可能是相机可见的。
9.2 漫反射 - Physically Based Rendering From Theory To Implementation(PBRT)
最新发布
Elsa的迷弟
03-23 236
翻译：https://pbr-book.org/4ed/Reflection_Models/Diffuse_Reflection总目录： Physically Based Rendering From Theory To Implementation - 基于物理的渲染从理论到实践第四版原书翻译最简单的BRDF之一是Lambertian模型，它描述了一个完美的漫反射表面，在所有方向上均匀散射入射光。它是许多真实表面(如纸张或哑光油漆)的合理近似。Lambertian模型相对较好地捕捉了这种漫反射材料的行为，
Physically Based Rendering From Theory To Implementation 基于物理的渲染，第十六章1/2
07-11
总计225M，18章，1000多页，这是第十六章两个压缩包中第一个 CHAPTER 16. LIGHT TRANSPORT I: SURFACE REFLECTION
附录C 场景描述处理 - Physically Based Rendering From Theory To Implementation(PBRT)
Elsa的迷弟
03-13 179
翻译：https://pbr-book.org/4ed/Processing_the_Scene_Description总目录： Physically Based Rendering From Theory To Implementation - 基于物理的渲染从理论到实践第四版原书翻译在本书开始的1.3.2节中讨论pbrt的main()函数时，我们写道，在处理命令行参数之后，场景描述被解析并转换为相应的形状、灯光、材料等。此后，正如我们已经讨论了这些类的实现一样，我们不再担心它们是何时创建的，或者它们的构
《Physically Based Rendering》翻译中文版——Introduction（介绍）
weixin_38401090的博客
06-06 7421
我自己在自学计算机图形学，现在正好学习到基于物理渲染这一块。在网上查阅大量的资料发现很少有中文的资料，想着趁着自己学习的时候，将这本书翻译过来帮助大家阅读和学习这本书中的内容。因个人能力和精力有限，在学习并翻译此书的过程中难免有一些失误，希望读者看到不妥之处，还请指正。我的邮箱：liupeicandy@163.com 原书网址：http://www.pbr-book.org/3ed-2018/In...
pbrt目录
xuexiaokkk的博客
08-20 749
提起PBRT(Physically Based Rendering: From Theory to Implementation)这本书, 在图形学业界可是鼎鼎大名, 该书获得2005年软件界Jolt图书类大奖. 这本书与众不同的是把当今图形学相当高级的理论成就联系到具体实现上来, 系统而又细致地阐述如何作出一流水准的图形渲染器的方方面面, 它所附带的pbrt库(http://www.pbrt
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值