9.9 头发散射 - Physically Based Rendering From Theory To Implementation(PBRT)

Physically Based Rendering From Theory To Implementation

翻译：https://pbr-book.org/4ed/Reflection_Models/Scattering_from_Hair

总目录： Physically Based Rendering From Theory To Implementation - 基于物理的渲染从理论到实践第四版原书翻译

9.9 Scattering from Hair 头发散射

人的头发和动物的皮毛可以用一个粗糙的介质界面来模拟，该界面围绕着一个有颜色的半透明的核心。对于所有的波长，界面的反射率通常是相同的，因此头发内部吸收的光量的波长变化决定了头发的颜色。虽然这些散射效果可以使用第11章和第14章的DielectricBxDF和体积散射模型的组合来建模，但这样做不仅计算成本高，需要在头发几何内部进行光线跟踪，而且对产生的模型进行重要性采样将是困难的。因此，本节介绍了一个专门的头发和毛皮的BSDF，它将这些较低层次的散射过程封装到一个可以有效地评估和采样的模型中。

如图9.39所示，是头发散射的视觉复杂性的一个例子，并与使用带有头发几何形状的传统BRDF模型进行渲染的比较。

图9.39:模拟头发的BSDF与涂层漫射BSDF(Coated Diffuse BSDF)的比较。(a)头发的几何模型，使用基于漫射基层的BSDF渲染，上面有一个粗糙的介电界面(第14.3.3节)。(b)使用本节的HairBxDF渲染的模型。因为HairBxDF是基于头发微观几何的精确模型，也模拟光通过头发的传输，它给了一个更真实的外观。(头发几何图形由Cem Yuksel提供。)

9.9.1 Geometry 几何

在讨论光在头发内散射的机制之前，我们将首先定义几种测量头发上光线交点的入射和出射方向的方法。在此过程中，我们将假设头发BSDF与6.7节中的曲线形状一起使用，这允许我们对头发几何的参数化做出假设。对于本节的几何讨论，我们将假设 Curve 变体对应于始终面对入射光线的平坦带状（flat ribbon）。然而，在BSDF模型中，我们将把交点解释为在相应的斜切圆柱体的表面上。如果头发之间没有交叉，并且头发的宽度不大于像素的宽度，那么在这些解释之间切换是没有坏处的。

在整个散射模型的实现过程中，我们发现将散射分别考虑纵向平面上的散射和方位平面上的散射是很有用的，前者有效地利用了曲线的侧面视图，后者考虑了曲线正对方向上某一点的散射。要理解这些参数化，首先回想一下曲线是参数化的，其方向 $u$ 是沿着曲线的长度，而且 $v$ 跨越其宽度。对于给定的 $u$，曲线所有可能的表面法向量都由圆截面在该点的表面法向量给出。所有这些法线都位于一个平面中，我们称之为法线平面(参见图9 - 40)。

图9.40:在曲线形状的任意参数点上，曲线的横截面用圆来定义。所有圆的表面法线(箭头)位于一个平面(虚线)，称为“法线平面”。

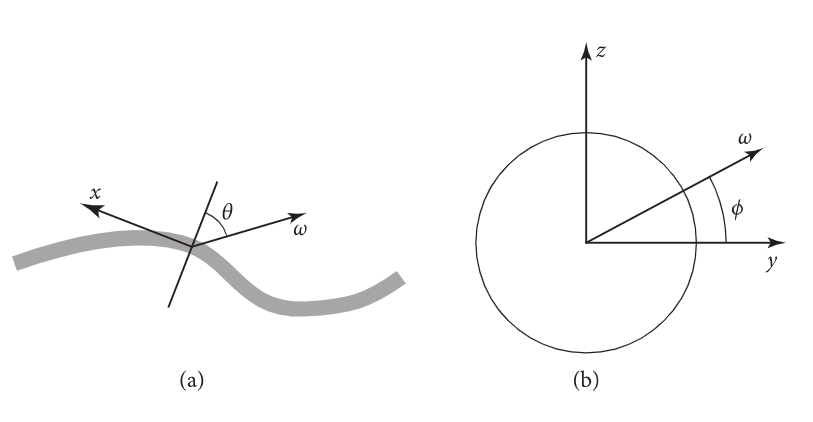
图9.41:(a)给定曲线上某一点的方向 $\omega$，纵向角 $\theta$ 由该点(粗线)法线平面与 $\omega$ 的夹角定义。曲线在该点处的切向量与BSDF坐标系中的x轴对齐。(b)对于一个方向 $\omega$，通过将该方向投影到法平面并计算其与y轴的夹角来求方位角 $\varphi$，该方位角对应于BSDF坐标系中的曲线的 $\partial p/\partial v$。

我们会发现用坐标$(\theta ,\varphi )$来表示射线曲线交点的方向是很有用的，这些坐标是在射线与曲线相交的u位置的法平面上定义的。角 $\theta$ 为纵向角，即为光线相对于法线面的偏移量(图9.41(a))；$\theta$ 的范围从 $-\pi /2$ 到 $\pi /2$ ，其中 $\pi /2$ 对应于与 $\partial p/\partial u$ 对齐的方向，而 $-\pi /2$ 对应于$-\partial p/\partial u$。如第9.1.1节所述，在pbrt的规则BSDF坐标系中，$\partial p/\partial u$ 与 $+x$ 轴对齐，因此在BSDF坐标系中给定一个方向，我们有$sin\theta ={\omega }_x$，因为法线平面垂直于 $\partial p/\partial u$。

在BSDF坐标系中，法线平面由y和z坐标轴组成。(y对应于曲线的 $\partial p/\partial v$ ，它总是垂直于曲线的 $\partial p/\partial u$ , z与带状法线对齐。)方位角 $\varphi$ 是通过将方向 $\omega$ 投射到法平面上并计算其与y轴的夹角来求出的。因此，它的范围从0到2π(图9.41(b))。

再对曲线进行一次测量将在下面有用。考虑某方向w的入射光线:在任意参数u值下，所有与曲线相交的光线都只能与沿曲线扫过的圆的一半相交(图9.42)。我们将用变量h来参数化圆的直径，其中$h=\pm 1$对应于擦过圆边缘的光线，$h=0$对应于侧着打到圆的光线。因为pbrt参数化曲线的 $v\in [0,1]$横跨曲线，我们可以计算 $h=-1+2\upsilon$。

给定射线交点$h$，我们可以计算推测出的斜截柱面的表面法线(根据定义在法线平面上)与方向 $\omega$ 之间的夹角，我们将用$\gamma$表示。(注意:这与第6.8节中用于浮点错误边界${\gamma }_n$的表示法无关。)如图9.42所示，显示了$sin\gamma =h$。

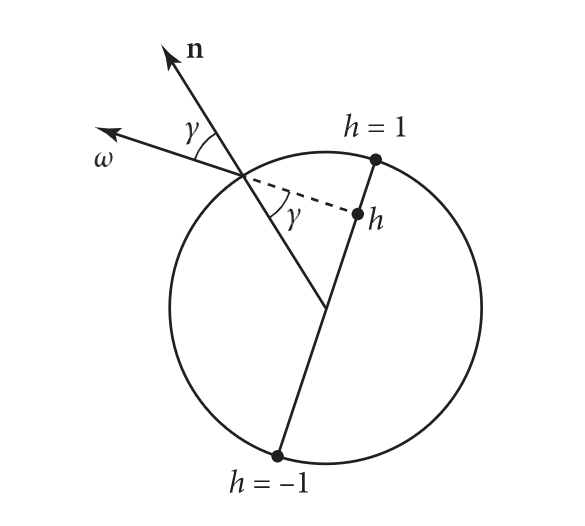
图9.42:给定一条射线的入射方向 $\omega$ ，它与投影到法线平面的一个 Curve （曲线）相交，我们可以用 $h\in [-1,1]$ 参数化曲线的宽度。给定一条与曲线相交的射线$h$，三角学告诉我们如何计算在曲线表面交点处的表面法线与 $\omega$ 之间的夹角$\gamma$。这两个角 $\gamma$ 相等，并且因为圆的半径是1，所有$sin\gamma =h$。

9.9.2 Scattering from Hair 头发散射

几何设置在手，我们现在将转向讨论一般散射行为，赋予头发其独特的外观和一些假设，我们将在以下做出。

头发和毛皮有三个主要成分:

• 角质层:与空气形成边界的外层。角质层的表面是一系列嵌套的鳞片，与毛发表面呈轻微的角度。
• 皮层:角质层内的下一层。皮层通常占头发总量的90%左右，但皮毛的比例更低。它通常通过主要吸收光线的色素来着色。
• 髓质:大脑皮层中间的核心。在较厚的毛发和皮毛中，它更大，更重要。髓质也有色素。来自髓质的散射比来自皮层介质的散射更重要。

对于下面的散射模型，我们做一些假设。(本章末尾的练习中讨论了放宽其中一些假设练习的方法。)首先，我们假设角质层可以建模为一个具有相同角度 $\alpha$ 的鳞片的粗糙介质圆柱体(实际上给出了一系列嵌套的锥形;参见图9 - 43)。我们还将头发内部视为仅吸收光线的均匀介质，并没有直接建模头发内部的散射。(第11章和第14章详细讨论了参与媒体的光传输。)

图9.43:头发的表面是由鳞片组成的，鳞片与理想的圆柱体有一个小角度 $\alpha$ 的偏离。( $\alpha$ 一般在紧贴表面;为了便于说明，此处显示的角度较大。)

我们还将假设散射可以通过BSDF精确建模——我们将光线建模为在同一位置进入和退出头发。(当然可以使用BSSRDF;“进一步阅读”部分提供了研究该替代方案的指针。)注意，这个假设要求头发的直径相对于表面光照变化的速度相当小;在典型的观测距离下，这种假设在实践中通常是正确的。

图9.44:到达头发的入射光可以以各种方式散射。$p=0$对应于角质层表面反射的光。光也可能通过头发折射而离开另一边：$p=1$。它可能被传送到头发里，然后再反射回来，然后再传送回来：$p=2$，等等。

到达头发的入射光在离开头发之前可能被散射一次或多次;图9.44显示了一些可能的情况。我们将使用 $p$ 来表示它在头发内部遵循的路径段的数量，然后再分散到空气中。我们有时会用一种简写来描述在边界处相应的散射事件:$p=0$对应于$R$，对于反射$p=1$是$TT$，对于两次传输$p=2$对应于$TRT$，$p=3$ 对应于$TRRT$，等等。

在下面，我们将单独考虑这些散射模式，因此将头发BSDF写成各项的 $p$ 的总和:

$$f({\omega }_o,{\omega }_i)=\sum _{p=0}^{\infty }{f}_p({\omega }_o,{\omega }_i)$$

$(9.47)$

为了使散射模型的评估和采样更容易，许多头发散射模型都将 $f$ 因素考虑在内 ，其中一个只取决于角度$\theta$，另一个取决于$\varphi$，$\varphi$为${\varphi }_o$和${\varphi }_i$之间的差异。该半可分离模型由下式给出:

$$f_p\left({\omega }_{\mathrm{o}},{\omega }_{\mathrm{i}}\right)=\frac{M_p\left({\theta }_{\mathrm{o}},{\theta }_{\mathrm{i}}\right)A_p\left({\omega }_{\mathrm{o}}\right)N_p(\varphi )}{\left|\cos {\theta }_{\mathrm{i}}\right|},$$
$(9.48)$

其中我们有一个纵向(longitudinal)散射函数$M_p$，一个衰减函数$A_p$和一个方位(azimuthal)散射函数$N_p$。除以$|cos{\theta }_i|$抵消了反射方程中相应的因子。

在下面的实现中，我们将计算式(9.47)中和的前几项，然后用单个项表示所有高阶项。pMax常数控制在切换之前评估多少。

<<HairBxDF Constants>>= 
static constexpr int pMax = 3;

HairBxDF中实现的模型由六个值参数化:

• h：射线与定向带相交的曲线宽度的$[-1,1]$的偏移量。
• eta：头发内部的折射率(通常为1.55)。
• sigma_a：头发内部的吸收系数，其中距离是相对于发丝圆柱直径测量的。(吸收系数将在11.1.1节中介绍。)
• beta_m：将毛发的纵向粗糙度，映射到范围 $[0,1]$ 内。
• beta_n：方位角粗糙度，也映射到 $[0,1]$ 。
• alpha：毛发表面上的小鳞片与基本柱面的偏移角度，以度表示(通常为2)。

<<HairBxDF Definition>>= 
class HairBxDF {
  public:
    <<HairBxDF Public Methods>> 
  private:
    <<HairBxDF Constants>> 
    <<HairBxDF Private Methods>> 
    <<HairBxDF Private Members>> 
};

除了初始化相应的成员变量之外，HairBxDF构造函数还执行一些额外值的预计算，这些值将对散射模型的采样和评估有用。相应的代码将被添加到下面的<<HairBxDF constructor implementation>>片段中，更接近定义和使用相应值的位置。注意，alpha不是存储在成员变量中;然而，它被用来计算一些派生量。

<<HairBxDF Private Members>>= 
Float h, eta;
SampledSpectrum sigma_a;
Float beta_m, beta_n;

我们将从计算BSDF的方法开始。

<<HairBxDF Method Definitions>>= 
SampledSpectrum HairBxDF::f(Vector3f wo, Vector3f wi,
                            TransportMode mode) const {
    <<Compute hair coordinate system terms related to wo>> 
    <<Compute hair coordinate system terms related to wi>> 
    <<Compute cos\theta_t for refracted ray>> 
    <<Compute \gamma_t for refracted ray>> 
    <<Compute the transmittance T of a single path through the cylinder>> 
    <<Evaluate hair BSDF>> 
}

在评估毛发散射模型时，需要一些与方向${\omega }_i$和${\omega }_o$相关的量——具体来说，是每个方向与垂直于曲线的平面形成的夹角 $\theta$ 的正弦和余弦，以及方位角坐标系中的角度$\varphi$。

如第9.9.1节所述，$sin{\theta }_o$由BSDF坐标系中 ${\omega }_o$ 的 $x$ 分量给出。已知 $sin{\theta }_o$，因为${\theta }_o\in [-\pi /2,\pi /2]$，我们知道 $cos{\theta }_o$ 一定是正的，所以我们可以用恒等式$si{n}^2\theta +co{s}^2\theta =1$来计算 $cos{\theta }_o$ 。垂直平面上的角度${\varphi }_o$可以用std::atan来计算。

<<Compute hair coordinate system terms related to wo>>= 
Float sinTheta_o = wo.x;
Float cosTheta_o = SafeSqrt(1 - Sqr(sinTheta_o));
Float phi_o = std::atan2(wo.z, wo.y);
Float gamma_o = SafeASin(h);

等效代码计算wi的这些值。

<<Compute hair coordinate system terms related to wi>>= 
Float sinTheta_i = wi.x;
Float cosTheta_i = SafeSqrt(1 - Sqr(sinTheta_i));
Float phi_i = std::atan2(wi.z, wi.y);

有了这些可用的值，我们将依次考虑BSDF模型的因素-$M_p$、$A_p$和$N_p$-，然后返回到 $f()$ 方法的完成。

9.9.3 Longitudinal Scattering 纵向散射

$M_p$定义与角度$\theta$相关的散射分量——纵向散射。纵向散射负责沿头发长度的镜面叶(specular lobe)，而纵向粗糙度 ${\beta }_m$ 控制这种高光的大小。图9.45显示了用三种不同的纵向散射粗糙度渲染的头发几何形状。


图9.45:改变纵向粗糙度${\beta }_m$的效果。被天空环境贴图照亮的头发模型使用多种纵向粗糙度渲染(a)头发的粗糙度很低，${\beta }_m=0.1$，看起来太有光泽，几乎是金属的。(b)${\beta }_m=0.25$，高光类似于典型的人类头发。©在高粗糙度${\beta }_m=0.7$下，毛发是不真实的平坦和漫反射。(头发几何图形由Cem Yuksel提供。)

散射模型推导的数学细节是复杂的，所以我们在这里不包括它们;和往常一样，“进一步阅读”部分有详细的参考资料。这里实现的模型的设计目标是规范化(确保节能和无能量损失)，并且可以直接对其进行采样。虽然这个模型不是直接基于头发散射光线的物理模型，但它很好地匹配了测量数据，并对粗糙度$v$进行了参数控制。

这与在先前的章节，$v$被用于沿着曲线宽度的参数化坐标不同。

模型为:

$$M_p\left({\theta }_{\mathrm{o}},{\theta }_{\mathrm{i}}\right)=\frac{1}{2v\sinh (1/v)}{\mathrm{e}}^{-\frac{\sin {\theta }_{\mathrm{i}}\sin {\theta }_{\mathrm{o}}}{v}}{I}_0\left(\frac{\cos {\theta }_{\mathrm{o}}\cos {\theta }_{\mathrm{i}}}{v}\right)$$

$(9.49)$

式中 $I_o$ 为第一类修正贝塞尔函数，$v$ 为粗糙度差额（variance）。图9.46显示了$M_p$的图表。

图9.46:纵向散射函数图。$M_p$的形状作为三个${\theta }_o$值的${\theta }_i$函数。在所有情况下，粗糙度差额 $v=0.02$ 都被使用。峰值从完美镜面反射方向(分别在 ${\theta }_i=1,1.3,1.4$)稍微偏移。(源自d’Eonet al. (2011)，图4。)

对于低粗糙度方差值，该模型在数值上不稳定，因此我们的实现使用了不同的方法来处理这种情况，即在最后取指数之前对对数$I_o$进行操作。下面实现中的v <= .1检验在两种公式之间进行选择。

<<HairBxDF Private Methods>>= 
Float Mp(Float cosTheta_i, Float cosTheta_o, Float sinTheta_i,
         Float sinTheta_o, Float v) {
    Float a = cosTheta_i * cosTheta_o / v, b = sinTheta_i * sinTheta_o / v;
    Float mp = (v <= .1) ?
               (FastExp(LogI0(a) - b - 1 / v + 0.6931f +
                        std::log(1 / (2 * v)))) :
               (FastExp(-b) * I0(a)) / (std::sinh(1 / v) * 2 * v);
    return mp;
}

该模型的一个挑战是选择粗糙度 $v$ 以实现所需的外观。在这里，我们实现了一个感知上均匀的映射，从粗糙度${\beta }_m\in [0,1]$到$v$，其中粗糙度$v=0$几乎是完全平滑的，$v=1$是极其粗糙的。不同的粗糙度值用于不同的 $p$ 值。对于$p=1$，粗糙度是通过一个经验因子来减少的，该因子模拟光线由于头发的圆形边界折射而形成的光线聚焦效果。然后因为$p=2$和后续项对它进行增加，以模拟光线在头发内部粗糙的圆柱体边界多次反射后扩散的效果。

<<HairBxDF constructor implementation>>= 
v[0] = Sqr(0.726f * beta_m + 0.812f * Sqr(beta_m) + 3.7f * Pow<20>(beta_m));
v[1] = .25 * v[0];
v[2] = 4 * v[0];
for (int p = 3; p <= pMax; ++p)
    v[p] = v[2];

<<HairBxDF Private Members>>+=  
Float v[pMax + 1];

9.9.4 Absorption in Fibers 纤维中的吸收

$A_p$ 因子描述入射光如何受到每种散射模式 $p$ 的影响。它结合了两种效果:头发与空气交界处的菲涅耳反射和折射，以及通过头发的光的吸收(对于$p>0$)。图9 - 47渲染了不同吸收系数的头发图像，展示了吸收的效果。我们已经实现的$A_p$函数将毛发边界上的所有反射和折射建模为完美镜面——这与$M_p$和(即将到来的)$N_p$模拟光滑反射和折射的假设非常不同。这个假设简化了实现，并在实践中给出了合理的结果(大概是因为高光路径在某种意义上是所有可能的光滑路径的平均值)。



图9.47:头发渲染不同的吸收系数。在所有情况下，${\beta }_m=0.25$,${\beta }_n=0.3$。(a) ${\sigma }_a=(3.35,5.58,10.96)$(RGB系数):在黑色头发中，几乎所有透射光都被吸收。$p=0$项的白色镜面高光是主要的视觉特征。(b) ${\sigma }_a=(0.84,1.39,2.74)$给出棕色头发，其中$p>1$项都是指头发的颜色。©很低的吸收系数${\sigma }_a=(0.06,0.10,0.20)$，我们是金发。(头发几何图形由Cem Yuksel提供。)

我们将从寻找通过头发的单个透射段路径后仍然存在的入射光的分数开始。要做到这一点，我们需要找出射线离开圆柱体之前的距离;最简单的方法是分别计算纵向和方位投影中的距离。

为了计算这些距离，我们需要光线${\omega }_o$在纵向平面和方位平面上的透射角度，我们将分别用${\theta }_t$和${\gamma }_t$表示。应用Snell定律，利用头发的折射率$\eta$，我们可以计算$sin{\theta }_t$和$cos{\theta }_t$。

<<Compute  for refracted ray>>= 
Float sinTheta_t = sinTheta_o / eta;
Float cosTheta_t = SafeSqrt(1 - Sqr(sinTheta_t));

对于${\gamma }_t$，虽然我们可以从${\omega }_o$计算透射方向${\omega }_t$，然后投影${\omega }_t$到法平面上，但也可以直接使用修正的折射率来计算${\gamma }_t$，它考虑了纵向角度对法平面上折射方向的影响。修正后的折射率由

$${\eta }^{\prime }=\frac{\sqrt{{\eta }^2-si{n}^2{\theta }_o}}{cos{\theta }_o}$$

已知${\eta }^{\prime }$，我们可以直接在法平面上计算折射方向${\gamma }_t$。因为$h=sin{\gamma }_o$，我们可以应用Snell定律来计算${\gamma }_t$。

<<Compute gamma_t for refracted ray>>= 
Float etap = SafeSqrt(Sqr(eta) - Sqr(sinTheta_o)) / cosTheta_o;
Float sinGamma_t = h / etap;
Float cosGamma_t = SafeSqrt(1 - Sqr(sinGamma_t));
Float gamma_t = SafeASin(sinGamma_t);

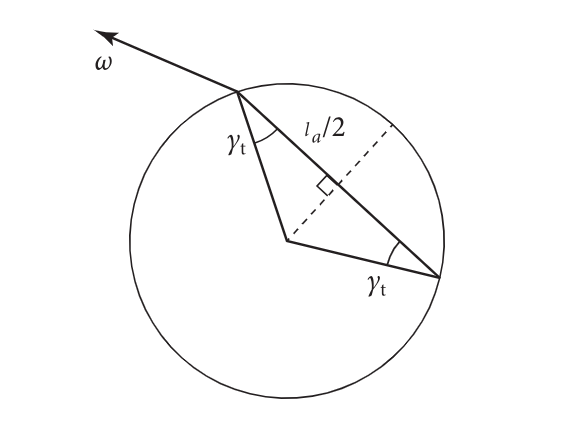
图9 - 48：计算传输段的距离。对于相对于圆表面法线有角度${\gamma }_t$的透射射线，假设是单位半径，总距离$l_a$的一半为$cos\gamma$。因为${\gamma }_t$与这两部分的长度是相同的，$l_a=2cos{\gamma }_t$。

如果我们考虑透射光线在法平面上的方位投影，我们可以看到这个线段在它的两端上与圆法线的角度${\gamma }_t$是相同的(参见图9 - 48)。如果我们用$l_a$表示这段的总长度，那么基本的三角学告诉我们，假设是一个单位半径的圆， $l_a/2=cos{\gamma }_t$。

图9 - 49：对传输段长度的影响${\theta }_t$。通过圆柱体的传输段的长度与直接垂直路径相比增加了一个因子$1/cos{\theta }_t$。

现在考虑纵向投影，我们可以看到，透射光线在穿过圆柱体之前传播的距离是按系数比例$1/cos{\theta }_t$缩放的(图9.49)。把这些放在一起，用头发直径表示的总长度是

$$l=\frac{2cos{\gamma }_t}{cos{\theta }_t}$$

已知段长和介质的吸收系数，可以用11.2节介绍的比尔定律计算透射光的分数。因为HairBxDF定义${\sigma }_a$为相对于头发直径进行测量(因此调整头发几何形状的宽度不会完全改变其颜色)，所以当我们应用Beer定律时，我们不考虑头发圆柱体直径，并且在段末端剩余的光的分数由下式给出：

$$T_r=e^{-{\sigma }_{a}l}.(9.50)$$

<<Compute the transmittance T of a single path through the cylinder>>= 
SampledSpectrum T = Exp(-sigma_a * (2 * cosGamma_t / cosTheta_t));

给定单个片段的透射率，我们现在可以描述评估整个$A_p$函数的函数。Ap()返回一个数组，其中的$A_p$值不超过$p_{max}$，最终值为所有高阶散射项的衰减之和。

<<HairBxDF Private Methods>>+=  
pstd::array<SampledSpectrum, pMax + 1>
Ap(Float cosTheta_o, Float eta, Float h, SampledSpectrum T) {
    pstd::array<SampledSpectrum, pMax + 1> ap;
    <<Compute p=0 attenuation at initial cylinder intersection>> 
    <<Compute p=1 attenuation term>> 
    <<Compute attenuation terms up to p=pMax>> 
    <<Compute attenuation term accounting for remaining orders of scattering>> 
    return ap;
}

对于这个$A_0$项，对应于在角质层反射的光，在空气-头发边界的菲涅耳反射率给出了被反射的光的比例。在毛发坐标系中，我们可以求出表面法线与夹角为${\theta }_o$和${\gamma }_o$的方向向量的夹角余弦值$cos{\theta }_{o}cos{\gamma }_o$。

<<Compute p=0 attenuation at initial cylinder intersection>>= 
Float cosGamma_o = SafeSqrt(1 - Sqr(h));
Float cosTheta = cosTheta_o * cosGamma_o;
Float f = FrDielectric(cosTheta, eta);
ap[0] = SampledSpectrum(f);

对于TT项，$p=1$，我们有两个$1-f$因子，一个是考虑进入和离开角质层边界的传播，另一个是考虑通过头发的一个传播路径的单一T因子。

<<Compute p=1 attenuation term>>= 
ap[1] = Sqr(1 - f) * T;

图9 - 50：透射光线在发筒内部发生镜面反射时，与原始透射光线与圆表面法线的角度${\gamma }_t$相同。由此可知，圆柱体内路径的所有射线段的长度必须相等。

$p=2$项有一个反射事件，将光反射回头发，然后是第二个折射项。因为我们假设角质层边界处有完美的镜面反射，所以头发内部的两个部分与圆的法线形成相同的角度${\gamma }_t$(参见图9 - 50)。由此我们可以看出，两个段的长度必须相同(后续的段也是如此)。一般来说，对于$p>0$，

$$A_p=A_{p-1}Tf=(1-f{)}^2{T}^p{f}^{p-1}.$$

<<Compute attenuation terms up to p=pMax>>= 
for (int p = 2; p < pMax; ++p)
    ap[p] = ap[p - 1] * T * f;

在pMax之后，最后一项解释了所有进一步的散射阶数。幸运的是，剩下的无穷级数的和可以以封闭形式找到，因为$T<1$且$f<1$:

$$\sum _{p=p_{max}}^{\infty }(1-f{)}^2{T}^p{f}^{p-1}=\frac{(1-f{)}^2{T}^{p_{max}}{f}^{p_{max}-1}}{1-Tf}$$

<<Compute attenuation term accounting for remaining orders of scattering>>= 
if (1 - T * f)
    ap[pMax] = ap[pMax - 1] * f * T / (1 - T * f);

9.9.5 Azimuthal Scattering 方位散射

图9 - 51：对于镜面反射，$p=0$，入射方向和反射方向与表面法线成同一角度${\gamma }_o$。因此净角度变化是 $-2{\gamma }_o$。对于$p=1$，射线在进入圆柱体时从${\gamma }_o$转向${\gamma }_t$，在出圆柱体时发生相应的偏转。我们还可以看到，当光线再次传出圆外时，它与表面法线形成了一个角度${\gamma }_o$。把角度加起来，净偏转是 $2{\gamma }_t-2{\gamma }_o+\pi$。

最后，我们将对依赖于角度 $\varphi$ 的散射分量进行建模。我们将完全在法平面上做这个工作。方位角散射模型是基于：首先计算一个新的方位角方向，假设完美的镜面反射和折射，然后定义围绕该中心方向的方向分布，其中粗糙度的增加使分布范围更广。因此，我们将首先考虑入射光线如何通过在法平面上的镜面反射和透射而偏转；$p$的前两个值的情况如图9.51所示。

根据图9.51的推理，我们可以推导出给出方位方向净变化量的函数 $\Phi$:

$$\Phi (p,h)=2p{\gamma }_t-2{\gamma }_o+p\pi$$

(回想一下，${\gamma }_o$和${\gamma }_t$是从哪里派生出来的。)图9 - 52给出了$p=1$时函数的图形。

图9 - 52：对$p=1$的$\Phi (p,h)$的绘制。当$h$从-1到1变化时，我们可以看到镜面透射射线的方向$\varphi$范围变化很快。通过检查$\varphi$值的范围，我们可以看到可能的传播方向大致覆盖了圆上$2/3$可能的方向。

<<HairBxDF Private Methods>>+=  
Float Phi(int p, Float gamma_o, Float gamma_t) {
    return 2 * p * gamma_t - 2 * gamma_o + p * Pi;
}

现在我们知道了如何在镜面折射和反射后计算法线平面上的新角度，我们需要一种方法来表示表面粗糙度，以便以镜面方向为中心的一系列方向可以有助于散射。logistic分布提供了一个很好的选择:它在渲染中通常很有用，因为它与高斯分布具有相似的形状，同时也被归一化并以闭合形式可积(与高斯分布不同);更多信息参见B.2.5节。

图9 - 53：在$[-\pi ,\pi ]$内裁剪后的（trimmed）Logistic函数。(蓝色线)$s=0.5$的曲线是宽阔而平坦的，而(红色线)$s=0.1$的曲线是尖峰的。由于函数是归一化的，与高斯函数不同，在0处的峰值通常不等于1。

在下面，我们会发现在一个范围 $[a,b]$ 内定义一个规范化的逻辑函数是很有用的；我们称其为 trimmed logistic(修整过的逻辑)，$l_t$。

$$l_{\mathrm{t}}(x,s,[a,b])=\frac{l(x,s)}{{\int }_a^{b}l\left(x^{\prime },s\right)\mathrm{d}{x}^{\prime }}$$

图9.53显示了几个S值的修整过的logistic分布图。

现在我们有了能够实现方位散射分布的部分。Np()函数计算 $N_p$ 项，计算$\varphi$和$\Phi (p,h)$之间的角度差，并计算该角度的方位角分布。

<<HairBxDF Private Methods>>+= 
Float Np(Float phi, int p, Float s, Float gamma_o, Float gamma_t) {
    Float dphi = phi - Phi(p, gamma_o, gamma_t);
    <<Remap dphi to [-pi,pi]>> 
    return TrimmedLogistic(dphi, s, -Pi, Pi);
}

$\varphi$和$\Phi (p,h)$之间的差值可能超出了我们定义的logistic范围，$[-\pi ,\pi ]$，因此我们需要围绕圆进行旋转，以使值达到正确的范围。因为对于这里使用的小值 $p$ 来说，dphi不会超出太远的范围，所以我们根据需要，使用简单的加减$2\pi$方法。

<<Remap dphi to [-pi,pi]>>= 
while (dphi > Pi) dphi -= 2 * Pi;
while (dphi < -Pi) dphi += 2 * Pi;

与纵向粗糙度一样，从方位粗糙度 ${\beta }_n\in [0,1]$ 到逻辑缩放因子 $s$ 有一个粗略的感知线性映射是有帮助的。

<<HairBxDF constructor implementation>>+=  
static const Float SqrtPiOver8 = 0.626657069f;
s = SqrtPiOver8 * (0.265f * beta_n + 1.194f * Sqr(beta_n) +
                   5.372f * Pow<22>(beta_n));

<<HairBxDF Private Members>>+=  
Float s;

图9 - 54：对于$p=1$的$N_p$极坐标图，${\theta }_o$与$-x$坐标轴对齐，粗糙度较小，${\beta }_n=0.1$，对于(蓝色) $h=-0.5$ 和(红色) $h=0.3$ 我们可以看到$N-p$随着头发的宽度变化很快。

图9 - 54显示了TT项的方位散射的极坐标图，$p=1$，粗糙程度相当低。曲线宽度上两个不同的点的散射分布有很大的不同。因为我们期望头发宽度大致为像素大小，所以每个像素需要许多射线才能很好地解决这种变化。

9.9.6 Scattering Model Evaluation 散射模型评估

我们现在几乎拥有了评估模型所需的所有部分。最后一个细节是考虑鳞片对毛发表面的影响(回想图9.43)。适当的调整 ${\theta }_o$ 可以很好地模拟头发的这种特征。

对于R项，对 ${\theta }_o$ 添加$2\alpha$角度可以模拟毛发散射模型相对于鳞片的表面法线的评估效果。然后我们可以继续对修改 ${\theta }_o$ 后的 $M_0$ 进行评估。对于$TT$，我们必须考虑两个通过鳞片的折射事件。在相反的方向旋转 $\alpha$ 近似补偿。(因为折射角相对于在法向的变化是非线性的，有因此这个近似由一些误差，虽然在$\alpha$值很小的典型情况下误差很低。) $TRT$ 在头发内有一个反射项；一个 $-4\alpha$ 旋转补偿了整体效果。

这些位移的影响是主反射瓣R被偏移到完美镜面方向之上，而次反射瓣R被偏移到完美镜面方向之下。由于R不受头发颜色的影响，而TRT由于吸收而拾取头发的颜色，因此，这两种颜色导致了两种不同颜色的明显高光。这种效果可以在人的头发中看到，并且在图9.45中的图像中很明显。

因为我们只需要${\theta }_i$角的正弦和余弦来计算 $M_p$，我们可以用三角恒等式

$$\begin{array}{l}\sin \left({\theta }_0\pm \alpha \right)=\sin {\theta }_0\cos \alpha \pm \cos {\theta }_0\sin \alpha \\ \cos \left({\theta }_0\pm \alpha \right)=\cos {\theta }_0\cos \alpha \mp \sin {\theta }_0\sin \alpha \end{array}$$

来有效地计算旋转角度，而不需要计算任何额外的三角函数。HairBxDF构造函数因此预先计算$k=0,1,2$的$sin(2^k\alpha )$和$cos(2^k\alpha )$。这些值可以用三角倍角恒等式特别有效地计算出来：$cos2\theta =co{s}^2\theta -si{n}^2\theta$和$sin2\theta =2cos\theta sin\theta$。

<<HairBxDF constructor implementation>>+= 
sin2kAlpha[0] = std::sin(Radians(alpha));
cos2kAlpha[0] = SafeSqrt(1 - Sqr(sin2kAlpha[0]));
for (int i = 1; i < pMax; ++i) {
    sin2kAlpha[i] = 2 * cos2kAlpha[i - 1] * sin2kAlpha[i - 1];
    cos2kAlpha[i] = Sqr(cos2kAlpha[i - 1]) - Sqr(sin2kAlpha[i - 1]);
}

<<HairBxDF Private Members>>+= 
Float sin2kAlpha[pMax], cos2kAlpha[pMax];

现在，对模型进行评估主要是调用已经定义好的函数，然后把每个 $f_p$ 项求和。

<<Evaluate hair BSDF>>= 
Float phi = phi_i - phi_o;
pstd::array<SampledSpectrum, pMax + 1> ap = Ap(cosTheta_o, eta, h, T);
SampledSpectrum fsum(0.);
for (int p = 0; p < pMax; ++p) {
    <<Compute sinθ_o and cosθ_o terms accounting for scales>> 
    fsum += Mp(cosTheta_i, cosThetap_o, sinTheta_i, sinThetap_o, v[p]) *
            ap[p] * Np(phi, p, s, gamma_o, gamma_t);
}
<<Compute contribution of remaining terms after pMax>> 
if (AbsCosTheta(wi) > 0)
    fsum /= AbsCosTheta(wi);
return fsum;

使用上面列出的三角恒等式实现的旋转可以解释鳞片(scale)的影响。下面是 $p=0$ 情况下的代码，其中${\theta }_o$被旋转 $2\alpha$。其余的情况遵循相同的结构。($p=1$时旋转$-\alpha$，$p=2$时旋转$-4\alpha$)

<<Compute sinθ_o and cosθ_o terms accounting for scales>>= 
Float sinThetap_o, cosThetap_o;
if (p == 0) {
    sinThetap_o = sinTheta_o * cos2kAlpha[1] - cosTheta_o * sin2kAlpha[1];
    cosThetap_o = cosTheta_o * cos2kAlpha[1] + sinTheta_o * sin2kAlpha[1];
}
<<Handle remainder of p values for hair scale tilt>> 
<<Handle out-of-range cosθ_o from scale adjustment>> 

当 ${\omega }_i$ 几乎与头发平行时，鳞片调整可能会对 $cos{\theta }_i$ 给出一个稍微负的值，在这种情况下，它表示 ${\theta }_i$ 略大于$\pi /2$，$\pi /2$是头发坐标系中的 $\theta$ 最大期望值。这个角等于 $\pi -\theta$，且 $cos(\pi -{\theta }_i)=|cos{\theta }_i|$，所以我们可以很容易地处理它。

<<Handle out-of-range cosθ_o from scale adjustment>>= 
cosThetap_o = std::abs(cosThetap_o);

最后一项解释了毛发内部的所有高阶散射。我们只用均匀分布 $N(\varphi )=1/(2\pi )$ 来表示方位分布；这是一个合理的选择，因为对于 $p\ge p_{max}$ 到 $\Phi (p.h)$ 的方向偏移量通常有很大的变化，最终$A_p$项通常代表不到15%的总散射，所以在最终结果中引入的误差很小。

<<Compute contribution of remaining terms after pMax>>= 
fsum += Mp(cosTheta_i, cosTheta_o, sinTheta_i, sinTheta_o, v[pMax]) *
        ap[pMax] / (2 * Pi);

互惠须知

虽然我们在4.3.1节中把互易性包含在物理有效的BRDFs属性中，但不幸的是，我们在本节中实现的模型不是互易的。一个迫在眉睫的问题是，毛发鳞片的旋转仅适用于${\theta }_i$。但是，还有更多的问题:首先，所有涉及传输的项$p>0$都不是相互的，因为传输项使用的值是基于${\omega }_t$的，而本身只依赖于${\omega }_o$。因此，如果${\omega }_o$和${\omega }_i$互换，则计算完全不同的${\omega }_t$，这反过来导致不同的$cos{\theta }_t$和${\gamma }_t$值，这反过来又提供与$A_p$和$N_p$函数不同的值。然而，在实践中，还没有从这些缺点中观察到图像中的伪影。

9.9.7 Sampling 采样

能够根据类似于整体BSDF的分布，生成采样方向，并计算给定方向采样的PDF，这对于高效渲染至关重要，特别是在低粗糙度情况下，其中头发BSDF作为方向的函数快速变化。在这里实现的方法中，样本的生成过程分为两步:首先，我们根据每个项的$A_p$函数值的概率选择一个p项进行采样，$A_p$函数值给出了它对整体散射函数的贡献。然后，通过对相应的$M_p$和$N_p$项进行采样来确定方向。幸运的是，头发BSDF的$M_p$和$N_p$项都可以被完美地采样，给我们留下了一个完全匹配完整BSDF的PDF的采样方案。

我们将首先定义ApPDF()方法，该方法返回一个离散的PDF，其中包含每个项$A_p$抽样的概率，根据其相对于所有$A_p$项的贡献，给定${\theta }_o$。

<<HairBxDF Method Definitions>>+=  
pstd::array<Float, HairBxDF::pMax + 1>
HairBxDF::ApPDF(Float cosTheta_o) const {
    <<Initialize array of A_p values for cosTheta_o>> 
    <<Compute A_p PDF from individual A_p terms>> 
    return apPDF;
}

该方法首先计算cosTheta_o的$A_p$的值。我们可以重用一些之前定义的片段来简化这个任务。

<<Initialize array of A_p values for cosTheta_o>>= 
Float sinTheta_o = SafeSqrt(1 - Sqr(cosTheta_o));
<<Compute cosθ_t for refracted ray>> 
<<Compute γ_t for refracted ray>> 
<<Compute the transmittance T of a single path through the cylinder>> 
pstd::array<SampledSpectrum, pMax + 1> ap = Ap(cosTheta_o, eta, h, T);

然后，利用光谱$A_p$值的亮度将光谱$A_p$值转换为标量，并对这些值进行归一化以生成合适的PDF。

<<Compute A_p PDF from individual A_p terms>>= 
pstd::array<Float, pMax + 1> apPDF;
Float sumY = 0;
for (const SampledSpectrum &as : ap)
    sumY += as.Average();
for (int i = 0; i <= pMax; ++i)
    apPDF[i] = ap[i].Average() / sumY;

有了这些准备工作，我们现在可以实现Sample_f()方法了。

<<HairBxDF Method Definitions>>+=  
pstd::optional<BSDFSample>
HairBxDF::Sample_f(Vector3f wo, Float uc, Point2f u, TransportMode mode,
                   BxDFReflTransFlags sampleFlags) const {
    <<Compute hair coordinate system terms related to wo>> 
    <<Determine which term p to sample for hair scattering>> 
    <<Compute sinθ_o and cosθ_o terms accounting for scales>> 
    <<Sample M_p to compute θ_i>> 
    <<Sample N_p to compute ▲φ>> 
    <<Compute wi from sampled hair scattering angles>> 
    <<Compute PDF for sampled hair scattering direction wi>> 
    return BSDFSample(f(wo, wi, mode), wi, pdf, Flags());
}

给定PDF的 $A_p$ 项，调用SampleDiscrete()负责选择一个。因为我们只需要从PDF的分布中生成一个样本，所以计算显式CDF数组(例如，通过使用PiecewiseConstant1D)的工作是不值得的。注意，我们利用了SampleDiscrete()的可选功能，即返回一个新的均匀随机样本，覆盖uc中的值。稍后将使用该样本值采样$N_p$。

<<Determine which term p to sample for hair scattering>>= 
pstd::array<Float, pMax + 1> apPDF = ApPDF(cosTheta_o);
int p = SampleDiscrete(apPDF, uc, nullptr, &uc);

我们现在可以对给定${\theta }_o$的相应 $M_p$ 项进行采样找到${\theta }_i$。这个采样方法的推导过程相当复杂，所以我们在这里既不介绍推导过程，也不介绍实现过程。这个片段<<Sample M_p to compute θ_i>>消耗了u[0]和u[1]两个采样值，并根据采样的方向初始化了变量sinTheta_i和cosTheta_i。

<<Sample M_p to compute θ_i>>= 
Float cosTheta = 1 + v[p] * std::log(std::max<Float>(u[0], 1e-5) +
                                     (1 - u[0]) * FastExp(-2 / v[p]));
Float sinTheta = SafeSqrt(1 - Sqr(cosTheta));
Float cosPhi = std::cos(2 * Pi * u[1]);
Float sinTheta_i = -cosTheta * sinThetap_o + 
                    sinTheta * cosPhi * cosThetap_o;
Float cosTheta_i = SafeSqrt(1 - Sqr(sinTheta_i));

接下来我们将对方位分布 $N_p$ 进行采样。对于项不超过$p_{max}$，给定 $\Phi (p.h)$，我们从以出口方向为中心的logistic分布中取一个采样。对于最后一项，我们从均匀分布中采样。

<<Sample N_p to compute ▲φ>>=
<<Compute γ_t for refracted ray>> 
Float dphi;
if (p < pMax)
    dphi = Phi(p, gamma_o, gamma_t) + SampleTrimmedLogistic(uc, s, -Pi, Pi);
else
    dphi = 2 * Pi * uc;

给定${\theta }_i$和${\varphi }_i$，我们可以计算采样方向wi。其中的数学运算与SphericalDirection()函数类似，但有两个重要的区别。首先，因为在这里$\theta$是相对于垂直于圆柱体的平面进行测量的，而不是圆柱体轴进行测量的，所以我们需要为相对于圆柱体轴的坐标计算$cos(\pi /2-\theta )=sin\theta$，而不是$cos\theta$。其次，因为hair shading坐标系统的$(\theta ,\varphi )$坐标是相对于$+x$轴定向的，因此传递给Vector3f构造函数的维度顺序需要进行相应的调整，因为从Sample＿f()返回的方向应该在BSDF坐标系统中。

<<Compute wi from sampled hair scattering angles>>= 
Float phi_i = phi_o + dphi;
Vector3f wi(sinTheta_i, cosTheta_i * std::cos(phi_i),
            cosTheta_i * std::sin(phi_i));

因为我们可以直接从 $M_p$ 和 $N_p$ 分布中采样，所以总的PDF是

$$\sum _{p=0}^{p_{\max }}{M}_p\left({\theta }_{\mathrm{o}},{\theta }_{\mathrm{i}}\right){\tilde{A}}_p\left({\omega }_{\mathrm{o}}\right)N_p(\varphi )$$

其中 ${\tilde{A}}_p$ 是归一化的PDF项。请注意，在评估PDF时， ${\theta }_o$ 必须将毛发鳞片考虑在内；这与BSDF求值的方式(和代码片段)相同。

<<Compute PDF for sampled hair scattering direction wi>>= 
Float pdf = 0;
for (int p = 0; p < pMax; ++p) {
    <<Compute sinθ_o and cosθ_o terms accounting for scales>> 
    <<Handle out-of-range cosθ_o from scale adjustment>> 
    pdf += Mp(cosTheta_i, cosThetap_o, sinTheta_i, sinThetap_o, v[p]) *
           apPDF[p] * Np(dphi, p, s, gamma_o, gamma_t);
}
pdf += Mp(cosTheta_i, cosTheta_o, sinTheta_i, sinTheta_o, v[pMax]) *
       apPDF[pMax] * (1 / (2 * Pi));

HairBxDF::PDF()方法执行相同的计算，因此这里不包括实现。

9.9.8 Hair Absorption Coefficients 头发吸收系数

头发的颜色是由皮层中的色素吸收光线的方式决定的，这反过来又由标准化吸收系数来描述，其中距离是根据头发直径来测量的。如果想要一个特定的头发颜色，那么在渲染图像中的标准化吸收系数和头发颜色之间存在一个非明显的关系。不仅改变吸收系数的光谱值会对单根头发的外观产生不可预测的联系，而且许多头发集合之间的多次散射对每个人的外观颜色都有显著的影响。因此，pbrt提供了两种更直观的方法来指定头发颜色。

第一种是基于人类头发的颜色是由两种色素的浓度决定的这一事实。真黑素的浓度是造成黑发、棕发和金发差异的主要因素。(黑头发的真黑素最多，金发的最少。白发则没有。)第二种色素是褐黑素，它使头发呈橙色或红色。HairBxDF类提供了一种方便的方法，使用用户提供的颜料浓度和颜料吸收系数的乘积来计算吸收系数。

补充知识：黑色素并不都是黑色，其中主要是两种，褐黑素（Pheomelanin）是红色的，另一种叫真黑素（Eumelanin），但同样并不就真的是黑色，两个亚种，一个是棕色，一个是黑色。头发的颜色取决于染色机黑色素的产量与不同种类颜料的搭配。

<<HairBxDF Method Definitions>>+= 
RGBUnboundedSpectrum HairBxDF::SigmaAFromConcentration(Float ce, Float cp) {
    RGB eumelaninSigma_a(0.419f, 0.697f, 1.37f);
    RGB pheomelaninSigma_a(0.187f, 0.4f, 1.05f);
    RGB sigma_a = ce * eumelaninSigma_a + cp * pheomelaninSigma_a;
    return RGBUnboundedSpectrum(*RGBColorSpace::sRGB, sigma_a);
}

图9 - 55：金色头发中多重散射的重要性(a)在头发内部渲染了多达三次反弹的光。(b)以多达50次反弹的光线渲染。在浅色头发中，多次散射的光线对其视觉外观有重要的贡献。因此，准确地渲染非常金色或白色的头发比渲染深色头发需要更多的计算。(头发几何由Cem Yuksel提供。)

真黑色素的浓度分别约为8、1.3和0.3，可以合理地表示黑色、棕色和金色的头发。然而，准确地绘制浅色头发需要模拟许多光线的相互反射;参见图9 - 55。

有时直接指定想要的发色也很有用;SigmaAFromReflectance()方法，这里没有包括，是基于预先计算的吸收系数对头发颜色的拟合。