OTFS调制中的干扰分析

Girl_We_Got_A

已于 2022-12-14 15:58:00 修改

阅读量2.3k

点赞数 8

分类专栏： OTFS经典论文文章标签： 5G 论文阅读

于 2022-09-30 23:50:47 首次发布

本文链接：https://blog.csdn.net/weixin_44520927/article/details/127125340

版权

OTFS经典论文专栏收录该内容

2 篇文章 5 订阅

订阅专栏

论文链接：https://ieeexplore.ieee.org/document/8424569/

摘要简单描述：

论文介绍了OTFS的基本输入输出关系，然后分析了使用理想波形以及矩形波成型的区别，区别就在于使用理想波形只存在多普勒间干扰（IDI），而使用矩形波形还会存在额外的载波间干扰（ICI）和符号间干扰（ISI）。

2.系统模型

这里作者首先给出了OTFS时频域的基本定义：

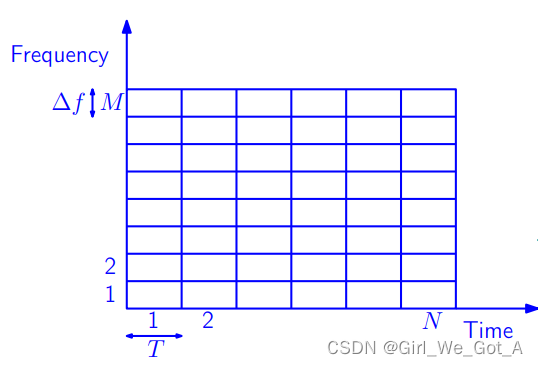
一个OTFS帧的时频域信号可以分别沿时域离散划分为 $N$ 个长度为 $T$ 的的块，沿频域离散划分为 $M$ 个长度为 $\Delta f$ 的块。所以一个OTFS帧的持续时间是 $T_{f}=NT$ ，占据了 $B=M\Delta f$ 的带宽。时频域信号划分如下图所示。

发送和接收滤波器分别用 $g_{tx}(t)$ 和 $g_{rx}(t)$ 表示，定义了它们的交叉模糊函数，如下

$A_{g_{\mathrm{rx}}, g_{\mathrm{tx}}}(t, f) \triangleq \int g_{\mathrm{rx}}^{*}\left(t^{\prime}-t\right) g_{\mathrm{tx}}\left(t^{\prime}\right) e^{-j 2 \pi f\left(t^{\prime}-t\right)} d t^{\prime}$

模糊函数本质上就是一个二维相关器（匹配滤波器），一维相关器只有时间一个变量，二维相关器则多了频率这个变量。所以模糊函数是一个关于时间和频率的函数，当接收滤波器的时间和频率都匹配上信道的时间和频率时才会达到A的最大值。

然后作者给出了OTFS时延多普勒域的基本定义：

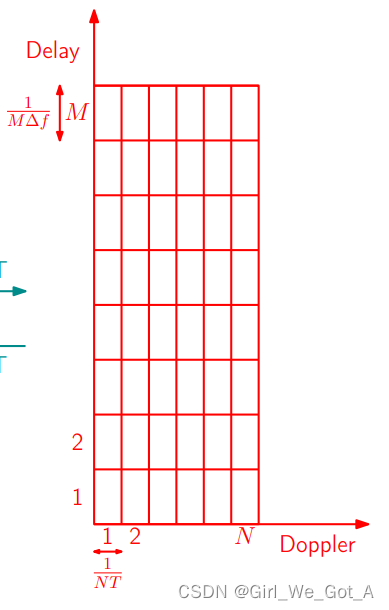
OTFS信号在延迟-多普勒域（Delay-Doppler，DD）中生成，同样可以将DD域沿多普勒域离散划分为 $N$ 个长度为 $\frac{1}{NT}$ 的块，沿时延域离散划分为 $M$ 个长度为 $\frac{1}{M\Delta f}$ 的块。如下图所示。所以多普勒域的长度是 $\frac{1}{T}$ ，时延域的长度是 $\frac{1}{\Delta f}$ ，这两个参数也就决定了OTFS最大可支持的多普勒与时延。

OTFS处理流程

论文里给出的调制解调流程如下图

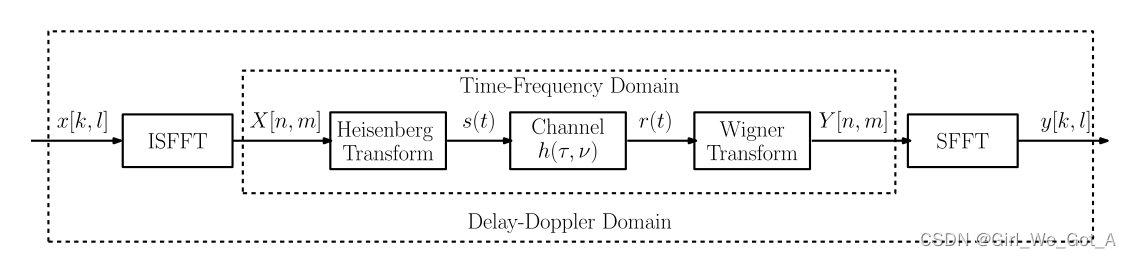
首先信号在DD域生成，然后经过经由ISFFT变换将信号转换到时频域，接下来应用海森堡变换将信号从时频域映射到时域。接收机执行相反的流程，首先将时域接收信号通过魏格纳变换映射回时频域信号，再经SFFT变换将信号转换回DD域。

$ISFFT$ ：

$X[n, m]=\frac{1}{\sqrt{N M}} \sum_{k=0}^{N-1} \sum_{l=0}^{M-1} x[k, l] e^{j 2 \pi\left(\frac{n k}{N}-\frac{m l}{M}\right)}$

可以理解为对 $l$ 进行 $M$ 点的 $DFT$ 和对 $k$ 进行 $N$ 点的 $IDFT$ ， $SFFT$ 执行逆过程。

海森堡变换：

$s(t)=\sum_{n=0}^{N-1} \sum_{m=0}^{M-1} X[n, m] g_{\mathrm{tx}}(t-n T) e^{j 2 \pi m \Delta f(t-n T)}$

当采用矩形波时可以替换为OFDM调制。

将时域信道建模为时间频率双选择性信道：

$h(\tau, \nu)=\sum_{i=1}^{P} h_{i} \delta\left(\tau-\tau_{i}\right) \delta\left(\nu-\nu_{i}\right)$

其中 $P$ 是信道径数， $\tau_{i}$ 表示第 $i$ 径的信道时延， $\nu_{i}$ 表示第 $i$ 径的多普勒频偏， $h_{i}$ 表示第 $i$ 径的幅度。

现在 $M$ 通常较大，故时延域的颗粒度 $\frac{1}{M\Delta f}$ 较细，于是我们认为信道每一径的时延都是 $\frac{1}{M\Delta f}$ 的整数倍，故可以把每一径的时延表示为 $\tau_{i}=\frac{l_{\tau_{i}}}{M \Delta f}$ ，其中 $l_{\tau_{i}}$ 是这一径的时延在时延域上的索引，即 $0,1,...,M-1$ 。现在 $N$ 通常较小，故此时多普勒域的颗粒度 $\frac{1}{NT}$ 较粗糙，不能再认为多普勒频移是 $\frac{1}{NT}$ 的整数倍，而应该是 $\frac{1}{NT}$ 的分数倍，即 $\nu_{i}=\frac{k_{\nu_{i}}+\kappa_{\nu_{i}}}{N T}$ ，其中 $k_{\nu_{i}}$ 表示这一径多普勒的整数索引（ $0,1,...,N-1$ ）， $\kappa_{\nu_{i}}$ 表示这一径多普勒的小数部分（取值±0.5之间）。如果信道中含有分数倍多普勒，那么就称多普勒域上的信道就不再稀疏，而时延域上的信道依然稀疏。

基于以上内容，论文给出了OTFS的时频域分析

OTFS时频域输入输出关系（稀疏表示）

$Y[n, m]=\sum_{n^{\prime}=0}^{N-1} \sum_{m^{\prime}=0}^{M-1} H_{n, m}\left[n^{\prime}, m^{\prime}\right] X\left[n^{\prime}, m^{\prime}\right]-------(1)$

其中，

$\begin{aligned} H_{n, m} & {\left[n^{\prime}, m^{\prime}\right] } \\ =& \iint h(\tau, \nu) A_{g_{\mathrm{rx}}, g_{\mathrm{tx}}}\left(\left(n-n^{\prime}\right) T-\tau,\left(m-m^{\prime}\right) \Delta f-\nu\right) \\ & \times e^{j 2 \pi\left(\nu+m^{\prime} \Delta f\right)\left(\left(n-n^{\prime}\right) T-\tau\right)} e^{j 2 \pi \nu n^{\prime} T} d \tau d \nu \end{aligned}$

其中， $\tau$ 和 $\nu$ 分别处于区间 $(-\tau_{\max }, \tau_{\max })$ 以及 $(-\nu_{\max }, \nu_{\max })$ 内。该时频域信道响应就是整合了海森堡变换、时域信道响应以及魏格纳变换的响应，具体推导过程可以看论文附录A。

3.理想脉冲的OTFS

首先给出满足双正交特性的波形条件：

$\begin{array}{r} \left.A_{g_{\mathrm{rx}}, g_{\mathrm{tx}}}(t, f)\right|_{t=n T+\left(-\tau_{\max }, \tau_{\max }\right), f=m \Delta f+\left(-\nu_{\max }, \nu_{\max }\right)}=\delta[n] \delta[m] q_{\tau_{\max }}(t) q_{\nu_{\max }}(f) \end{array}$

其中，当 $x\epsilon (-a,a)$ 时， $q_{a}(x)=1$ ，否则为0。分两种情况讨论，当n和m都是不为0的整数时，因为 $T$ 远大于 $\tau_{\max }$ 且 $\Delta f$ 远大于 $\nu_{\max }$ ，所以此时两个q函数就都为0；当n和m都得0时，此时，两个q函数都为1，整个交叉模糊函数的值就是一个冲激。最后的结论是：两个满足双正交特性的波形的交叉模糊函数仅在 $(-\tau_{\max }, \tau_{\max })$ 以及 $(-\nu_{\max }, \nu_{\max })$ 内是一个冲激，其他区间内值都是0。但是根据雷达理论，不存在理想的模糊函数，即不存在仅仅只由冲激函数组成的模糊函数，再理想的模糊函数也是有旁瓣的，不可能像冲激函数一样。

基于理想脉冲的假设，论文分别分析了时频域与DD域的信道响应

时频域：将双正交波形的假设带入(1)中时频域信道响应的表达式，可见交叉模糊函数仅仅在 $n^{'}=n$ 且 $m^{'}=m$ 时才有值，那么信道响应H也仅仅在 $n^{'}=n$ 且 $m^{'}=m$ 时才有值，再带入(1)中。原本 $Y[n, m]$ 应该由 $M*N$ 项的和构成，采用理想波形后就仅剩下了一项，即

$Y[n, m]=H_{n, m}\left[n, m\right] X\left[n, m\right]$

DD域：先给出DD域的信道响应，同理，DD域的信道响应就是在时频域信道响应基础上加上 $ISFFT$ 与 $SFFT$ 变换。可以证明，对于理想脉冲，DD域的输入输出关系如下

$y[k, l]=\frac{1}{N M} \sum_{k^{\prime}=0}^{N-1} \sum_{l^{\prime}=0}^{M-1} x\left[k^{\prime}, l^{\prime}\right] h_{w}\left[k-k^{\prime}, l-l^{\prime}\right]-----(2)$

其中， $h_{w}$ 由下面的式子组成

$h_{w}\left[k-k^{\prime}, l-l^{\prime}\right]=\left.h_{w}(\nu, \tau)\right|_{\nu=\frac{k-k^{\prime}}{N T}, \tau=\frac{l-l^{\prime}}{M \Delta f}}$

$\begin{aligned} h_{w}(\nu, \tau) &=\sum_{i=1}^{P} h_{i} e^{-j 2 \pi \nu_{i} \tau_{i}} w\left(\nu-\nu_{i}, \tau-\tau_{i}\right) \\ &=\sum_{i=1}^{P} h_{i} e^{-j 2 \pi \nu_{i} \tau_{i}} \mathcal{G}\left(\nu, \nu_{i}\right) \mathcal{F}\left(\tau, \tau_{i}\right), \end{aligned}$

$\mathcal{F}$ 和 $\mathcal{G}$ 和分别由下式给出

$\mathcal{F}\left(\frac{l-l^{\prime}}{M \Delta f}, \tau_{i}\right)=\sum_{m^{\prime}=0}^{M-1} e^{j \frac{2 \pi}{M}\left(l-l^{\prime}-l_{\tau_{i}}\right) m^{\prime}}=\frac{e^{j 2 \pi\left(l-l^{\prime}-l_{\tau_{i}}\right)}-1}{e^{j \frac{2 \pi}{M}\left(l-l^{\prime}-l_{\tau_{i}}\right)}-1}$

可以验证，只有当 $l-l^{'}-l_{\tau _{i}}$ 等于0或者 $M$ 的整数倍时， $\mathcal{F}$ 整个式子等于 $M$ ，等于其他数（除了 $M$ ）的整数倍的情况都是0。

$\mathcal{G}\left(\frac{k-k^{\prime}}{N T}, \nu_{i}\right)=\frac{e^{-j 2 \pi\left(k-k^{\prime}-k_{\nu_{i}}-\kappa_{\nu_{i}}\right)}-1}{e^{-j \frac{2 \pi}{N}\left(k-k^{\prime}-k_{\nu_{i}}-\kappa_{\nu_{i}}\right)}-1} .$

本来只要 $k-k^{'}-k_{\nu _{i}}-\kappa _{\nu _{i}}$ 也等于0或者 $N$ 的整数倍时， $\mathcal{G}$ 的整个式子也可以等于 $N$ ，等于其他数（除了 $N$ ）的整数倍的情况都是0。但是现在由于小数倍频偏的存在， $k-k^{'}-k_{\nu _{i}}-\kappa _{\nu _{i}}$ 肯定不可能等于0或者 $N$ 的整数倍，那么 $\mathcal{G}$ 的整个式子就不等于0。

这种存在小数倍多普勒频偏的情况也称为多普勒的弥散现象，现在再来看式(2)，原本 $y[k, l]$ 应该是 $M*N$ 项的线性组合，现在由于时延不存在小数倍的情况，故 $y[k, l]$ 可以简化为 $N$ 项的和。由此可见，这 $N$ 项全部是由同一时延的不同多普勒频偏项组成，所以有结论：当信道多普勒弥散时，同一时延上的不同多普勒符号间都会相互干扰，这种情况称作多普勒间干扰（ $IDI$ ）。

如果此时恰好信道中的多普勒是整数倍的，那么就不会出现多普勒间干扰， $y[k, l]$ 也就只剩下了一项。

4.矩形波形的OTFS

基于理想波形无法实现这一事实，下面论文给出了通用的矩形波形的相关分析。矩形脉冲仅在 $[0,T]$ 内有值，其余位置为0。

时频域：同样从交叉模糊函数入手，观察(1)中的时频域信道响应，如下

根据信号与系统，两个矩形的卷积（相关）的结果是一个三角形，且仅仅在 $[-T,T]$ 内有值。下面应用到模糊函数，前面说过交叉模糊函数等价于一个二维的相关器，那么二维相关器输出的模就呈现出一个三角形，且仅仅在 $[-T,T]$ 内有值。带入到 $A_{g_{\mathrm{rx}}, g_{\mathrm{tx}}}\left(\left(n-n^{\prime}\right) T-\tau,\left(m-m^{\prime}\right) \Delta f-\nu\right)$ 中，可以得出：只有 $n^{'}=n$ 以及 $n^{'}=n-1$ 时 $t$ 才位于 $[-T,T]$ 内，此时交叉模糊函数才不为0，其余时刻都为0。带 $n^{'}=n$ 以及 $n^{'}=n-1$ 入(1)中，有如下式子

$\begin{aligned} Y[n, m]=& \sum_{n^{\prime}=n-1}^{n} \sum_{m^{\prime}=0}^{M-1} H_{n, m}\left[n^{\prime}, m^{\prime}\right] X\left[n^{\prime}, m^{\prime}\right] \\ =& H_{n, m}[n, m] X[n, m] \\ &+\sum_{m^{\prime}=0, m^{\prime} \neq m}^{M-1} H_{n, m}\left[n, m^{\prime}\right] X\left[n, m^{\prime}\right] \\ &+\sum_{m^{\prime}=0}^{M-1} H_{n, m}\left[n-1, m^{\prime}\right] X\left[n-1, m^{\prime}\right] \end{aligned}$

首先，原来 $Y[n, m]$ 有 $M*N$ 项，现在简化为 $2M$ 项。第二个等式的前两项是 $n^{'}=n$ 的情况，第三项是 $n^{'}=n-1$ 的情况。其中，第一项是 $n^{'}=n$ 且 $m^{'}=m$ 的情况，第二项是 $n^{'}=n$ 且 $m^{'}\neq m$ 的情况。因此，第二项是同一符号其他载波的干扰，称为载波间干扰（ $ICI$ ）。第三项是其他符号的所有子载波对当前符号的干扰，称为符号间干扰（ISI）。

DD域：DD域的输入输出关系如下，具体证明见附录C

$\begin{array}{r} y[k, l] \approx \sum_{i=1}^{P} \sum_{q=-N_{i}}^{N_{i}} h_{i} e^{j 2 \pi\left(\frac{l-l_{\tau_{i}}}{M}\right)\left(\frac{k_{\nu_{i}}+\kappa_{\nu_{i}}}{N}\right)} \alpha_{i}(k, l, q) \\ \times x\left[\left[k-k_{\nu_{i}}+q\right]_{N},\left[l-l_{\tau_{i}}\right]_{M}\right] \end{array}----(3)$

$\begin{aligned} \alpha_{i}(k, l, q) &=\left\{\begin{array}{ll} \frac{1}{N} \beta_{i}(q) & l_{\tau_{i}} \leq l<M \\ \frac{1}{N}\left(\beta_{i}(q)-1\right) e^{-j 2 \pi \frac{\left[k-k_{\nu_{i}}+q\right]_{N}}{N}} & 0 \leq l<l_{\tau_{i}} \end{array}\right.\\ \beta_{i}(q) &=\frac{e^{-j 2 \pi\left(-q-\kappa_{\nu_{i}}\right)}-1}{e^{-j \frac{2 \pi}{N}\left(-q-\kappa_{\nu_{i}}\right)}-1} \end{aligned}$

注意到（3）中的指数项，从时频域到DD域的转换将 $ICI$ 与 $ISI$ 转换为了一个相位差。

Girl_We_Got_A

关注

8
点赞
踩
42

收藏

觉得还不错? 一键收藏
打赏
2
评论
OTFS调制中的干扰分析

OTFS的经典论文分析：Interference Cancellation and Iterative Detection for Orthogonal Time Frequency Space Modulation本文介绍了OTFS的基本输入输出关系，然后分析了使用理想波形以及矩形波成型的区别，区别就在于使用理想波形只存在多普勒间干扰（IDI），而使用矩形波形还会存在额外的载波间干扰（ICI）和符号间干扰（ISI）。
复制链接

扫一扫