【通信原理 入坑之路】—— 从频域角度深入理解调制解调过程

写在前面：本博文是《深入浅出通信原理》的学习笔记，仅供个人学习记录使用

一、从频域角度理解调制过程

先回顾一下用实数运算实现BPSK调制的框图：

还记得我们讲BPSK调制的时候，都是假的与$cos{\omega }_{0}t$相乘的都是直流分量+1或-1，但是真实传输过程中往往没有那么简单，经常会是一些非周期信号。我们假设$x(t)$的频谱如下所示：

我们通过上篇博文学习到的傅里叶变换，看看这个非周期的复杂信号$x(t)$和余弦载波$cos{\omega }_{0}t$相乘之后的频谱有什么特征：
$$\begin{array}{rl}{X}^{\prime }(\omega )& ={\int }_{-\infty }^{+\infty }x(t)cos{\omega }_{0}t{e}^{-j\omega t}dt\\ & ={\int }_{-\infty }^{+\infty }x(t)\frac{1}{2}(e^{j{\omega }_{0}t}+e^{-j{\omega }_{0}t})e^{j\omega t}dt\\ & =\frac{1}{2}{\int }_{-\infty }^{+\infty }x(t)e^{j({\omega }_0-\omega )t}dt+\frac{1}{2}{\int }_{-\infty }^{+\infty }x(t)e^{-j(\omega +{\omega }_0)t}dt\\ & =\frac{1}{2}{\int }_{-\infty }^{+\infty }x(t)e^{-j(\omega -{\omega }_0)t}dt+\frac{1}{2}{\int }_{-\infty }^{+\infty }x(t)e^{-j(\omega +{\omega }_0)t}dt\\ & =\frac{1}{2}X(\omega -{\omega }_0)+\frac{1}{2}X(\omega +{\omega }_0)\end{array}$$
通过对$x(t)cos{\omega }_{0}t$的傅里叶变换，我们发现：当信号$x(t)$与$cos{\omega }_{0}t$相乘之后，相当于将$x(t)$的频谱$X(\omega )$一分为二，分别向左和向右移动${\omega }_0$（也要注意幅度的变换：二分之一！）

【注意：如果频谱用的是$X(f)$表示，那么就相当于$X(f)$一分为二，分别向左和向右移动f】！

那么乘上了载波$cos{\omega }_{0}t$之后的频谱变为：

1.1 调制过程中频谱变化的Matlab展示

我们先来看看一个脉冲宽度为1的矩形波和频率$f_c$ = 5Hz的载波相乘的频谱变化：

%%%下面先从时域上来看看x(t)与余弦载波相乘的结果：%%%
subplot(3,1,1);
t = -1.5:0.01:1.5;
y = rectpuls(t, 1);
plot(t, y);
axis([-1.5 1.5 -0.5 1.5]);
grid on;

subplot(3,1,2);
carrier = cos(2*pi*5*t);     %fc = 5;
plot(t, carrier);
grid on;
axis([-1.5 1.5 -1.5 1.5]);

subplot(3,1,3);
st = y.*carrier;
plot(t, st);
grid on;
axis([-1.5 1.5 -1.5 1.5]);

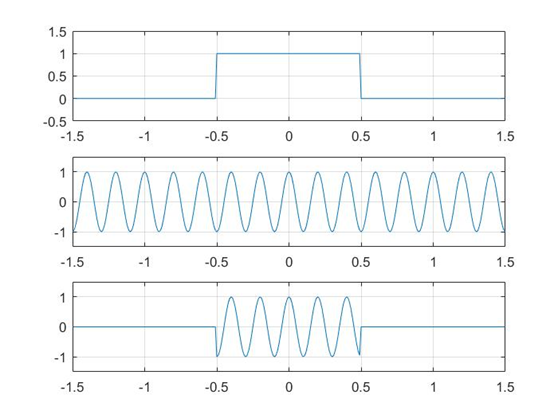
从之前的学习中我们知道：矩形波信号的频谱是：$$X(f)=\tau sinc(\tau f)$$
其中，$\tau$是脉冲宽度，那么对于上面这个脉冲宽度为1的矩形波$x(t)$，它的频谱就可以表示为：$sinc(f)$，代码如下：

figure(2);
k = -12:0.001:12;
xf = sinc(k);
plot(k, xf);
axis([-12,12,-0.3,1]);
grid on;

它与载波相乘之后，$X^{\prime }(f)$相当于原频谱一分为二，分别向左和向右移动f的过程，因此，有：

figure(3);
xf_new = 0.5.*sinc(k - 5) + 0.5*sinc(k + 5);
plot(k, xf_new);
axis([-12,12,-0.3,1]);
grid on;

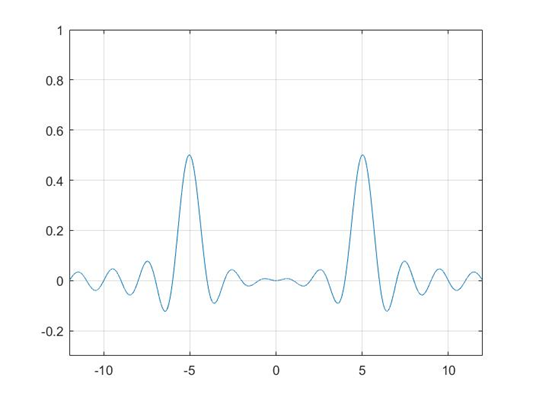
为了便于对比，我们将这两个频谱放到一起：

1.2从频域角度看x(t)与余弦载波相乘

关于从时域上理解BPSK调制解调，可以参考：
【通信原理 入坑之路】 —— 深入理解BPSK调制和解调的全过程及其Matlab实现
时域上，将$x(t)$信号和余弦载波$cos{\omega }_{0}t$相乘的时域波形是这样的：

下面，我们从三维空间看看正负脉冲和余弦载波相乘的频谱：

%下面是正脉冲的情况%
f = -9:0.001:-1;
x = 0.5*sinc(f+5);
fill3(x,f,0*f,'r');
hold on;
f = 1:0.001:9;
x = 0.5*sinc(f - 5);
xlabel('x'); ylabel('f'); zlabel('y')
grid on;
fill3(x,f,0*f,'r');
set(gca, 'YDir', 'reverse');

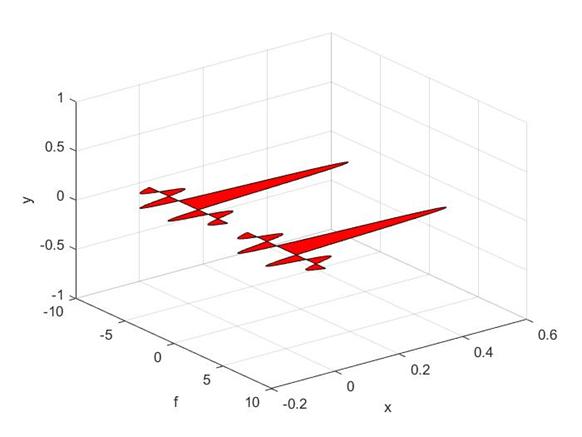
%下面是负脉冲的情况%
f = -9:0.001:-1;
x = -0.5*sinc(f+5);
fill3(x,f,0*f,'r');
hold on;
f = 1:0.001:9;
x = -0.5*sinc(f - 5);
xlabel('x'); ylabel('f'); zlabel('y')
grid on;
fill3(x,f,0*f,'r');
set(gca, 'YDir', 'reverse');

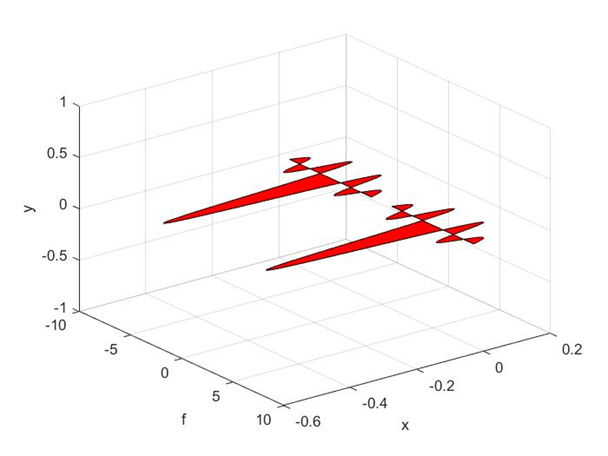
1.3 从频域角度看x(t)与正弦载波相乘

我们看看Q路信号与正弦载波$sin({\omega }_{0}t)$相乘的频谱变化：

$$\begin{array}{rl}{X}^{\prime }(\omega )& ={\int }_{-\infty }^{+\infty }x(t)sin{\omega }_{0}t{e}^{-j\omega t}dt\\ & ={\int }_{-\infty }^{+\infty }x(t)(-\frac{j}{2})(e^{j{\omega }_{0}t}-e^{-j{\omega }_{0}t})e^{-j\omega t}dt\\ & ={\int }_{-\infty }^{+\infty }x(t)(-\frac{j}{2})e^{j({\omega }_0-\omega )t}dt+{\int }_{-\infty }^{+\infty }x(t)\frac{j}{2}{e}^{-j({\omega }_0+\omega )t}dt\\ & ={\int }_{-\infty }^{+\infty }x(t)(-\frac{j}{2})e^{-j(\omega -{\omega }_0)t}dt+{\int }_{-\infty }^{+\infty }x(t)\frac{j}{2}{e}^{-j({\omega }_0+\omega )t}dt\\ & =-\frac{j}{2}X(\omega -{\omega }_0)+\frac{j}{2}X(\omega +{\omega }_0)\end{array}$$
我们发现，信号与正弦载波$sin({\omega }_{0}t)$相乘，频谱的变化有两个：

1. 原频谱$X(f)$一分为二，分别向左和向右平移f个单位
2. 向右平移的频谱需要在徐虚轴平面顺时针旋转90°；向左平移的频谱需要在虚轴平面逆时针旋转90°

下面我们从三维角度看看信号与正弦载波相乘的频谱：

%下面是正脉冲的情况%
f = -9:0.001:-1;
st1 = 0.5*sinc(f+5);
fill3(0*f,f,st1, 'b');
grid on;
hold on;
f = 1:0.001:9;
st2 = -0.5*sinc(f-5);
fill3(0*f,f,st2,'b');
grid on;
set(gca,'YDir','reverse');

下面，我们将I路信号与余弦载波$cos{\omega }_{0}t$相乘的频谱、Q路信号与$sin({\omega }_{0}t)$相乘的频谱画在一起：

1.4 QPSK调制的频谱

首先对下面的代码进行一些解释：
我们在本博客里面的仿真，比如说BPSK调制解调还是QPSK调制解调的频域分析，我们都默认I路，Q路信号都是脉冲宽度为1的矩形波，因此，I路信号和Q路信号的频谱都可以用sinc函数表示。

因此，下面代码中的xf_cos就表示：$Icos({\omega }_{0}t)$的频谱，xf_sin就表示$Qsin({\omega }_{0}t)$的频谱
或者我们这样想：$Icos({\omega }_{0}t)$的频谱就是上图那些红色的图，$Qsin({\omega }_{0}t)$的频谱就是上图那些蓝色的图，那么由于$s(t)=Icos({\omega }_{0}t)+Qsin({\omega }_{0}t)$因此，频谱也是对应地叠加。（向量相加）

那么，我们只需要将这两个频谱叠加（类似于向量的合成），那么我们就可以得到调制信号的频谱了

%发送数据10
subplot(2,2,1);
a = 1/sqrt(2);
f = -9:0.001:-1;
xf_cos = 0.5*a*sinc(f+5);
xf_sin = 0.5*a*sinc(f+5);
fill3(xf_cos,f,xf_sin,'g');
hold on;
f = 1:0.001:9;
xf_cos = 0.5*a*sinc(f-5);
xf_sin = -0.5*a*sinc(f-5);
fill3(xf_cos,f,xf_sin,'g');
grid on;
set(gca,'YDir','reverse');
title('发送数据10');

%发送数据11
subplot(2,2,2);
f = -9:0.001:-1;
xf_cos = -0.5*a*sinc(f+5);
xf_sin = 0.5*a*sinc(f+5);
fill3(xf_cos,f,xf_sin,'g');
hold on;
f = 1:0.001:9;
xf_cos = -0.5*a*sinc(f-5);
xf_sin = -0.5*a*sinc(f-5);
fill3(xf_cos,f,xf_sin,'g');
grid on;
set(gca,'YDir','reverse');
title('发送数据11');

%发送数据01
subplot(2,2,3);
f = -9:0.001:-1;
xf_cos = -0.5*a*sinc(f+5);
xf_sin = -0.5*a*sinc(f+5);
fill3(xf_cos,f,xf_sin,'g');
hold on;
f = 1:0.001:9;
xf_cos = -0.5*a*sinc(f-5);
xf_sin = 0.5*a*sinc(f-5);
fill3(xf_cos,f,xf_sin,'g');
grid on;
set(gca,'YDir','reverse');
title('发送数据01');

%发送数据00
subplot(2,2,4);
f = -9:0.001:-1;
xf_cos = 0.5*a*sinc(f+5);
xf_sin = -0.5*a*sinc(f+5);
fill3(xf_cos,f,xf_sin,'g');
hold on;
f = 1:0.001:9;
xf_cos = 0.5*a*sinc(f-5);
xf_sin = 0.5*a*sinc(f-5);
fill3(xf_cos,f,xf_sin,'g');
grid on;
set(gca,'YDir','reverse');
title('发送数据00');

【这里还需要特别说明一个问题】：大家现在要记得QPSK的映射关系：

输入二进制信号	I, Q信号
00	+$\frac{1}{\sqrt{2}}$, +$\frac{1}{\sqrt{2}}$
01	-$\frac{1}{\sqrt{2}}$,+$\frac{1}{\sqrt{2}}$
11	-$\frac{1}{\sqrt{2}}$,-$\frac{1}{\sqrt{2}}$
10	+$\frac{1}{\sqrt{2}}$,-$\frac{1}{\sqrt{2}}$

那么，对于上面的程序，当输入10时，由于我们在和载波$sin({\omega }_{0}t)$相乘时还需要对Q路信号乘上一个负号，因此，当Q路信号是负数时，相当于一个正的脉冲和$sin({\omega }_{0}t)$，那么问题来了：我们解调的时候，如果接收端Q路信号乘以的本地载波是$sin({\omega }_{0}t)$，那么此时解调出来的应该是-Q！！

这个问题我们一会儿会遇到。

二、从频域角度理解解调

我们从BPSK解调入手，还记得我们在之前的博文中从时域上分析BPSK解调吗：
对接收到的$s(t)=x(t)cos{\omega }_{0}t$，我们对它再乘以个本地载波$cos{\omega }_{0}t$，然后通过一个周期内积分再乘以2就可以解调出信号，那么，用低通滤波器的方法是什么原理呢？

这是$x(t)$经过BPSK调制，乘上了载波信号之后，在解调端再乘上了本地余弦信号之后的结果，仅仅靠乘上$cos{\omega }_{0}t$，似乎还并不能分离出$x(t)$，而低通滤波器，就可以把高频成分滤去，只留下$x(t)$。

因此，调制解调的原理如下：

其中，我们使用的低通滤波器的内部结构如下图所示：

2.1 频域角度理解QPSK解调

还是以发送信号10为例：
我们把$s(t)$分别在接收端乘以$cos({\omega }_{0}t)$和$sin({\omega }_{0}t)$，我们来看看解调结果：

我们还是来回顾一下发送信号10时，$s(t)$的频谱：

figure(1);
a = 1/sqrt(2);
f = -6:0.001:-4;
xf = 0.5*a*sinc(f+5);
yf = 0.5*a*sinc(f+5);
fill3(xf,f,yf,'b');
hold on;
f = 4:0.001:6;
xf = 0.5*a*sinc(f-5);
yf = -0.5*a*sinc(f-5);
fill3(xf,f,yf,'b');
grid on;
axis([-0.6 0.6 -12 12 -0.6 0.6]);
set(gca,'YDir','reverse');
line([0 0],[-12 12],[0 0]);

对这个$s(t)$信号再乘上$cos({\omega }_{0}t)$，我们可以这样理解，把上图这两个蓝色分量分别乘上$cos({\omega }_{0}t)$，然后进行向量合成，最后效果应该是这样：

f = -11:0.001:-9;
xf = 0.25*a*sinc(f+10);
yf = 0.25*a*sinc(f+10);
fill3(xf,f,yf,'b');
hold on;
f = 9:0.001:11;
xf = 0.25*a*sinc(f-10);
yf = -0.25*a*sinc(f-10);
fill3(xf,f,yf,'b');
hold on;
f = -1:0.001:1;
xf = 0.25*a*sinc(f)+0.25*a*sinc(f);
yf = 0.25*a*sinc(f)-0.25*a*sinc(f);
fill3(xf,f,yf,'b');
grid on;
set(gca,'YDir','reverse');
axis([-0.6 0.6 -12 12 -0.6 0.6]);
line([0 0],[-12 12],[0 0]);

然后，将这个信号经过傅里叶变换得到上面这个频谱，经过低通滤波器就可以得到+I信号了
下面我们来看看$s(t)$乘上$sin({\omega }_{0}t)$的结果：

figure(2);
%下面开始解调
a = 1/sqrt(2);
f = -11:0.001:-9;
xf = 0.25*a*sinc(f+10);
yf = -0.25*a*sinc(f+10);
fill3(xf,f,yf,'b');
hold on;
f = -1:0.001:1;
xf = 0.25*a*sinc(f);
yf = 0.25*a*sinc(f);
fill3(xf,f,yf,'b');
grid on;
axis([-0.6 0.6 -12 12 -0.6 0.6]);
set(gca,'YDir','reverse');
line([0 0],[-12 12],[0 0]);

figure(3);
f = -1:0.001:1;
xf = 0.25*a*sinc(f);
yf = -0.25*a*sinc(f);
fill3(xf,f,yf,'b');
hold on;
f = 9:0.001:11;
xf = -0.25*a*sinc(f-10);
yf = -0.25*a*sinc(f-10);
fill3(xf,f,yf,'b');
grid on;
axis([-0.6 0.6 -12 12 -0.6 0.6]);
set(gca,'YDir','reverse');
line([0 0],[-12 12],[0 0]);

figure(4);
f = -11:0.001:-9;
xf = -0.25*a*sinc(f+10);
yf = 0.25*a*sinc(f+10);
fill3(xf,f,yf,'b');
hold on;
f = 9:0.001:11;
xf = -0.25*a*sinc(f-10);
yf = 0.25*a*sinc(f-10);
fill3(xf,f,yf,'b');
hold on;
f = -1:0.001:1;
xf = 0.25*a*sinc(f)+0.25*a*sinc(f);
yf = 0.25*a*sinc(f)-0.25*a*sinc(f);
fill3(xf,f,yf,'b');
grid on;
set(gca,'YDir','reverse');
axis([-0.6 0.6 -12 12 -0.6 0.6]);
line([0 0],[-12 12],[0 0]);

我们最后得到的频谱是：

再经过低通滤波器滤去高频分量，就可以得到-Q信号了。最后再取个负，我们就正式完成了I, Q的解调了！